1.3交集、并集 学案（含答案）

《1.3交集、并集 学案（含答案）》由会员分享，可在线阅读，更多相关《1.3交集、并集 学案（含答案）（8页珍藏版）》请在七七文库上搜索。

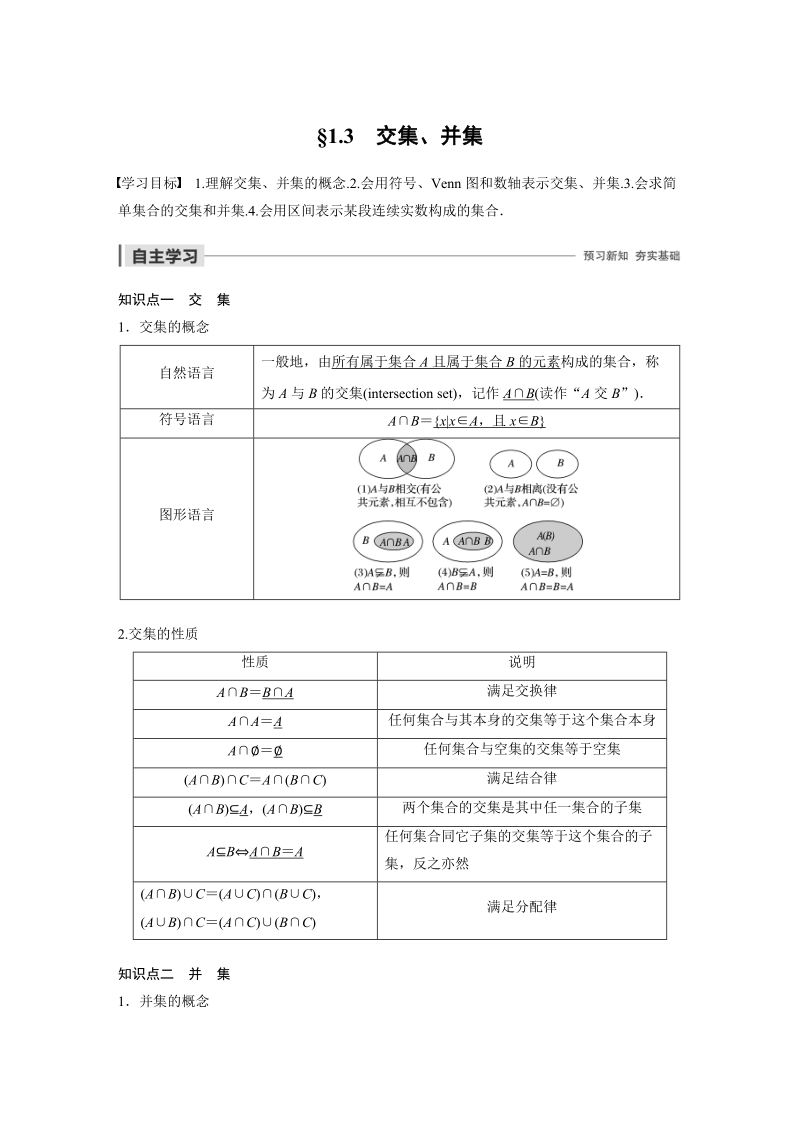
1、1.3交集、并集学习目标1.理解交集、并集的概念.2.会用符号、Venn图和数轴表示交集、并集.3.会求简单集合的交集和并集.4.会用区间表示某段连续实数构成的集合知识点一交集1交集的概念自然语言一般地，由所有属于集合A且属于集合B的元素构成的集合，称为A与B的交集(intersection set)，记作AB(读作“A交B”)符号语言ABx|xA，且xB图形语言2.交集的性质性质说明ABBA满足交换律AAA任何集合与其本身的交集等于这个集合本身A任何集合与空集的交集等于空集(AB)CA(BC)满足结合律(AB)A，(AB)B两个集合的交集是其中任一集合的子集ABABA任何集合同它子集的交集等

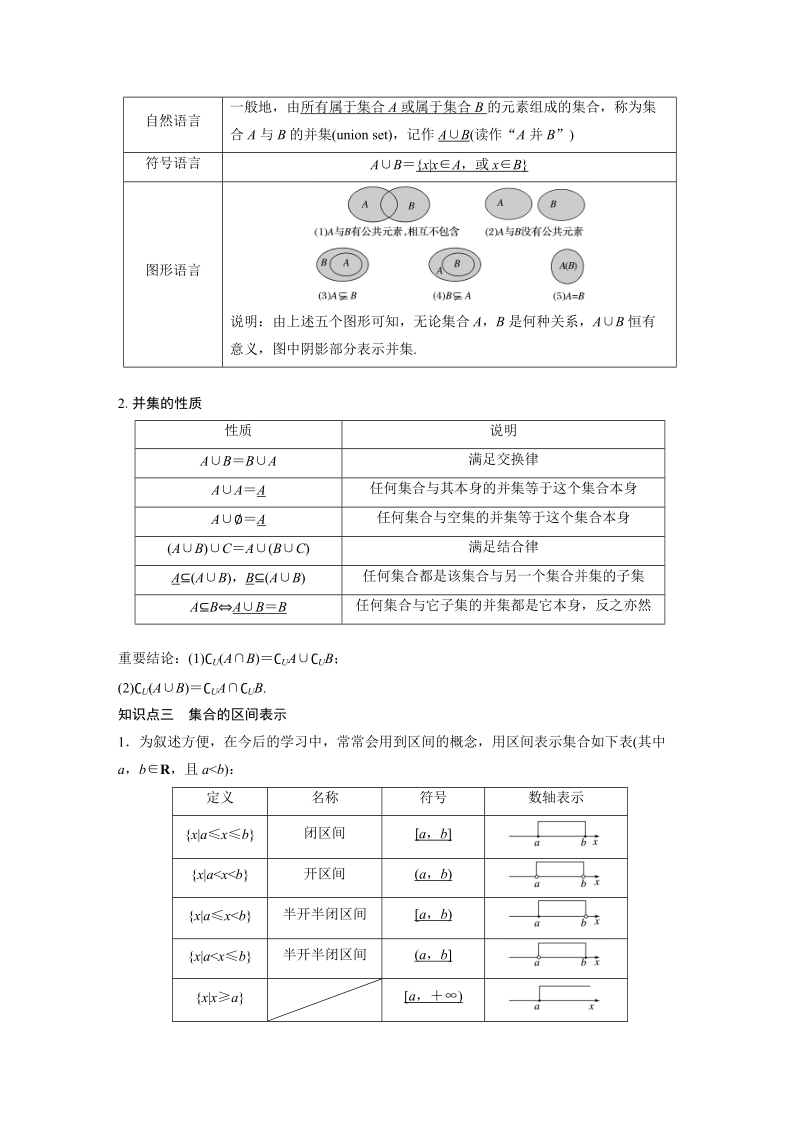
2、于这个集合的子集，反之亦然(AB)C(AC)(BC)，(AB)C(AC)(BC)满足分配律知识点二并集1并集的概念自然语言一般地，由所有属于集合A或属于集合B的元素组成的集合，称为集合A与B的并集(union set)，记作AB(读作“A并B”)符号语言ABx|xA，或xB图形语言说明：由上述五个图形可知，无论集合A，B是何种关系，AB恒有意义，图中阴影部分表示并集.2.并集的性质性质说明ABBA满足交换律AAA任何集合与其本身的并集等于这个集合本身AA任何集合与空集的并集等于这个集合本身(AB)CA(BC)满足结合律A(AB)，B(AB)任何集合都是该集合与另一个集合并集的子集ABABB任何

3、集合与它子集的并集都是它本身，反之亦然重要结论：(1)U(AB)UAUB；(2)U(AB)UAUB.知识点三集合的区间表示1为叙述方便，在今后的学习中，常常会用到区间的概念，用区间表示集合如下表(其中a，bR，且ab)：定义名称符号数轴表示x|axb闭区间a，bx|axb开区间(a，b)x|axb半开半闭区间a，b)x|aa(a，)x|xa(，ax|xa(，a)R(，)取遍数轴上所有的值2.注意：“”读作无穷大，是一个符号，不是数，以或作为区间一端时，这一端必须是小括号区间是数集的另一种表示方法，区间的两个端点必须保证左小、右大.题型一集合的交集、并集运算例1(1)已知U1,2,3,4,5,6

4、,7,8，A3,4,5，B4,7,8，求AB，AB，(UA)(UB)，A(UB)，(UA)B.解方法一AB4，AB3,4,5,7,8，UA1,2,6,7,8，UB1,2,3,5,6，(UA)(UB)1,2,6，A(UB)3,5，(UA)B1,2,4,6,7,8方法二AB，AB，A(UB)求法同方法一(UA)(UB)U(AB)1,2,6，(UA)BU(A(UB)1,2,4,6,7,8方法三画出Venn图，如图所示，可得AB4，AB3,4,5,7,8，(UA)(UB)1,2,6，A(UB)3,5，(UA)B1,2,4,6,7,8(2)已知全集Ux|x4，集合Ax|2x3，Bx|3x2，求AB，(U

5、A)B，A(UB)解如图，在数轴上表示集合A，B，U.Ax|2x3，Bx|3x2，UAx|x2，或3x4，UBx|x3，或2x4ABx|2x2，(UA)Bx|x2，或3x4，A(UB)x|2x3(3)若集合A(x，y)|3x2y1，B(x，y)|xy2，C(x，y)|2x2y3则AB_，BC_.答案(1，1)解析联立解得故AB(1，1)同理B，C联立无解，故BC.(4)(2018南通高一检测)某班有学生55人，其中体育爱好者43人，音乐爱好者34人，还有4人既不爱好体育又不爱好音乐，则该班既爱好体育又爱好音乐的人数为_答案26解析设Ax|x为体育爱好者，Bx|x为音乐爱好者则UAUBx|x为既

6、不爱好体育又不爱好音乐由Venn图可知，既爱好体育又爱好音乐的人数为：(4334)(554)26(人)反思感悟(1)若集合是用列举法给出的有限集进行交、并、补运算时，关键是正确理解交集、并集、补集的含义(2)若集合是用描述法表示的不等式数集进行交、并、补运算时，应利用好数轴这一工具跟踪训练1(1)设集合A4,5,6,8，B3,5,7,9，则AB_，AB_.答案53,4,5,6,7,8,9(2)已知全集UR，集合Ax|x1，Bx|12x15求：AB；AB；(UA)(UB)解因为Ax|x1，Bx|1x2，所以ABx|1x2ABx|x1因为UAx|x1，UBx|x1，或x2，所以(UA)UBx|x1

7、(3)设集合A(x，y)|yax1，B(x，y)|yxb，且AB(2,5)，则()Aa3，b2 Ba2，b3Ca3，b2 Da2，b3答案B解析AB(2,5)，解得a2，b3，故选B.(4)某班有36名同学参加数学、物理、化学课外探究小组，每名同学至多参加两个小组，已知参加数学、物理、化学小组的人数分别为26,15,13，同时参加数学和物理小组的有6人，同时参加物理和化学小组的有4人，则同时参加数学和化学小组的有_人答案8解析设参加数学、物理、化学小组的人数构成的集合分别为A，B，C，同时参加数学和化学小组的有x人，由题意可得如图所示的Venn图由全班共36名同学可得(266x)6(1510)

8、4(134x)x36，解得x8，即同时参加数学和化学小组的有8人题型二由集合的并集、交集求参数例2(1)集合Aa2，a1，1，B2a1，|a2|,3a24，AB1，则a的值是_答案0解析由AB1，得1B.因为|a2|0,3a240，所以2a11，解得a0，这时A0,1，1，B1,2,4，则AB1成立(2)已知集合Ax|1x6，Bx|2x10，Cx|xa求(RA)B.若ACC，求a的取值范围解因为Ax|1x6，Bx|2x10，所以RAx|x1或x6，所以(RA)Bx|6x10因为ACC，所以AC.又因为Ax|1x6，Cx|xa，所以a6.引申探究把例(2)中条件“ACC”改为“(RA)CC”，其

9、他条件不变，求a的取值范围解因为(RA)CC，所以CRA.又因为RAx|x1或x6，Cx|xa，所以a1.反思感悟(1)题目中若有条件ABB和ABB，一般都等价转化为BA和AB.(2)在包含关系BA中，不要漏掉B的情况跟踪训练2(1)(2017全国)设集合A1,2,4，Bx|x24xm0若AB1，则B等于()A1，3 B1,0 C1,3 D1,5答案C解析AB1，1B.14m0，即m3.Bx|x24x301,3故选C.(2)已知Ax|2axa3，Bx|x5，若ABB，求a的取值范围解ABBAB.当2aa3，即a3时，A，满足AB.当2aa3，即a3时，A6，满足AB.当2aa3，即a3时，要使

10、AB，需或解得a4或a3a|a3.1对交集、并集概念的理解(1)AB中的元素是“所有”属于集合A且属于集合B的元素，而不是部分，特别地，当集合A和集合B没有公共元素时，不能说A与B没有交集，而是AB.(2)对于并集，要注意其中“或”的意义，“或”与通常所说的“非此即彼”有原则性的区别，它们是“相容”的“xA，或xB”这一条件，包括下列三种情况：xA但xB；xB但xA；xA且xB.因此，AB是由所有至少属于A，B两者之一的元素组成的集合2集合的交、并运算中的注意事项(1)对于元素个数有限的集合，可直接根据集合的“交”“并”定义求解，但要注意集合元素的互异性(2)对于元素个数无限的集合，进行交、并

11、运算时，可借助数轴，利用数轴分析法求解，但要注意端点值取到与否1(2018全国)已知集合A0,2，B2，1,0,1,2，则AB等于()A0,2 B1,2C0 D2，1,0,1,2答案A解析AB0,22，1,0,1,20,2故选A.2已知集合Mx|3x5，Nx|x5或x5，则MN等于()Ax|x5或x3 Bx|5x5Cx|3x5 Dx|x3或x5答案A解析在数轴上表示集合M，N，如图所示，则MNx|x5或x33集合Ax|1x2，Bx|x1，则A(RB)_.(用区间表示)答案1,2解析Bx|x1，RBx|x1A(RB)x|1x24若集合A0,1,2，x，B1，x2，ABA，则满足条件的实数x有_个答案2解析A0,1,2，x，B1，x2，ABA，BA，x20或x22或x2x，解得x0或或或1.经检验当x或时满足题意5已知集合Ax|1x3，Bx|m2xm2(1)若ABx|1x3，求实数m的值；(2)若AB，求实数m的取值范围解Ax|1x3，Bx|m2xm2(1)ABx|1x3，解得m3.(2)AB，Ax|xm2m23或m25或m3.