第2章 圆锥曲线与方程 章末复习学案（含答案）

《第2章 圆锥曲线与方程 章末复习学案（含答案）》由会员分享，可在线阅读，更多相关《第2章 圆锥曲线与方程 章末复习学案（含答案）（12页珍藏版）》请在七七文库上搜索。

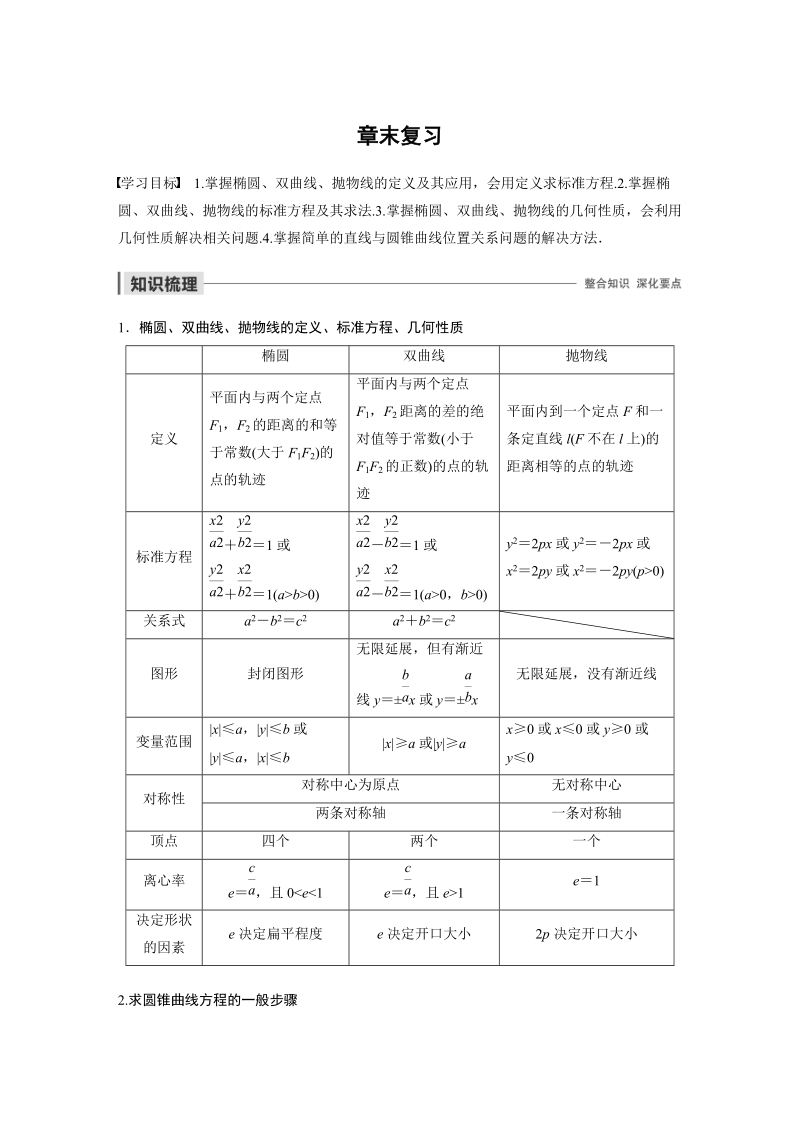
1、章末复习学习目标1.掌握椭圆、双曲线、抛物线的定义及其应用，会用定义求标准方程.2.掌握椭圆、双曲线、抛物线的标准方程及其求法.3.掌握椭圆、双曲线、抛物线的几何性质，会利用几何性质解决相关问题.4.掌握简单的直线与圆锥曲线位置关系问题的解决方法1椭圆、双曲线、抛物线的定义、标准方程、几何性质椭圆双曲线抛物线定义平面内与两个定点F1，F2的距离的和等于常数(大于F1F2)的点的轨迹平面内与两个定点F1，F2距离的差的绝对值等于常数(小于F1F2的正数)的点的轨迹平面内到一个定点F和一条定直线l(F不在l上)的距离相等的点的轨迹标准方程1或1(ab0)1或1(a0，b0)y22px或y22px或

2、x22py或x22py(p0)关系式a2b2c2a2b2c2图形封闭图形无限延展，但有渐近线yx或yx无限延展，没有渐近线变量范围|x|a，|y|b或|y|a，|x|b|x|a或|y|ax0或x0或y0或y0对称性对称中心为原点无对称中心两条对称轴一条对称轴顶点四个两个一个离心率e，且0e1e1决定形状的因素e决定扁平程度e决定开口大小2p决定开口大小2.求圆锥曲线方程的一般步骤一般求已知曲线类型的曲线方程问题，可采用“先定形，后定式，再定量”的步骤(1)定形指的是二次曲线的焦点位置与对称轴的位置(2)定式根据“形”设方程的形式，注意曲线系方程的应用，如当椭圆的焦点不确定在哪个坐标轴上时，可设

3、方程为mx2ny21(m0，n0且mn)(3)定量由题设中的条件找到“式”中待定系数的等量关系，通过解方程得到量的大小3离心率(1)定义法：由椭圆(双曲线)的标准方程可知，不论椭圆(双曲线)的焦点在x轴上还是y轴上都有关系式a2b2c2(a2b2c2)以及e，已知其中的任意两个参数，可以求其他的参数，这是基本且常用的方法(2)方程法：建立参数a与c之间的齐次关系式，从而求出其离心率，这是求离心率的十分重要的思路及方法(3)几何法：求与过焦点的三角形有关的离心率问题，根据平面几何性质以及椭圆(双曲线)的定义、几何性质，建立参数之间的关系，通过画出图形，观察线段之间的关系，使问题更形象、直观4焦点

4、三角形(1)椭圆的焦点三角形设P为椭圆1(ab0)上任意一点(不在x轴上)，F1，F2为焦点且F1PF2，则PF1F2为焦点三角形(如图)焦点三角形的面积为Sb2tan .焦点三角形的周长为L2a2c.(2)双曲线的焦点三角形焦点三角形的面积为S.5直线与圆锥曲线的位置关系直线与圆锥曲线的位置关系，主要是直线与椭圆的位置关系，涉及函数、方程、不等式、平面几何等诸多方面的知识，形成了求定值、最值、对称、取值范围、线段的长度等多种问题解决此类问题应注意数形结合，以形辅数的方法；还要多结合圆锥曲线的定义，利用“设而不求法”以及“点差法”等 1椭圆x24y21的离心率为.()2抛物线y24x的焦点到准

5、线的距离是4.()3若椭圆x2my21的离心率为，则它的长半轴长为2.()4双曲线1(2t1)和双曲线y21(n0)有相同的焦点F1，F2，P是它们的一个交点，则F1PF2的形状是_答案直角三角形解析设P为双曲线右支上的一点对椭圆y21(m1)，c2m1，PF1PF22；对双曲线y21，c2n1，PF1PF22.PF1，PF2，F1F(2c)22(mn)而PFPF2(mn)(2c)2F1F，F1PF2是直角三角形类型二圆锥曲线的性质及其应用例2(1)已知ab0，椭圆C1的方程为1，双曲线C2的方程为1，C1与C2的离心率之积为，则C2的渐近线的斜率为_(2)已知抛物线y24x的准线与双曲线y2

6、1交于A，B两点，点F为抛物线的焦点，若FAB为直角三角形，则该双曲线的离心率为_答案(1)(2)解析(1)ab0，椭圆C1的方程为1，C1的离心率为.双曲线C2的方程为1，C2的离心率为.C1与C2的离心率之积为，2，C2的渐近线的斜率为.(2)抛物线y24x的准线方程为x1.又FAB为直角三角形，则只有AFB90，如图，则A(1,2)在双曲线上，代入双曲线方程可得a2，于是c.故e.反思与感悟有关圆锥曲线的焦点、离心率、渐近线等问题是考试中常见的问题，只要掌握基本公式和概念，并且充分理解题意，大都可以顺利求解跟踪训练2已知F1(c,0)，F2(c,0)为椭圆1(ab0)的两个焦点，P为椭圆

7、上一点，且c2，则此椭圆离心率的取值范围为_答案解析设P(x，y)，则(cx，y)(cx，y)x2c2y2c2，将y2b2x2代入式，解得x2，又x20，a2，2c2a23c2，e.类型三直线与圆锥曲线的位置关系命题角度1有关基本量的计算问题例3已知椭圆1(ab0)上的点P到左、右两焦点F1，F2的距离之和为2，离心率为.(1)求椭圆的标准方程；(2)过右焦点F2的直线l交椭圆于A，B两点，若y轴上一点M满足MAMB，求直线l的斜率k的值解(1)由题意知，PF1PF22a2，所以a.又因为e，所以c1，所以b2a2c2211，所以椭圆的标准方程为y21.(2)已知椭圆的右焦点为F2(1,0)，

8、直线斜率显然存在，设直线的方程为yk(x1)，两交点坐标分别为A(x1，y1)，B(x2，y2)联立直线与椭圆的方程，得化简得(12k2)x24k2x2k220，8k280.所以x1x2，y1y2k(x1x2)2k.所以AB的中点坐标为.当k0时，AB的中垂线方程为y，因为MAMB，所以点M在AB的中垂线上，将点M的坐标代入直线方程，得，即2k27k0，解得k或k；当k0时，AB的中垂线方程为x0，满足题意所以斜率k的取值为0，或.反思与感悟解决圆锥曲线中的参数范围问题与求最值问题类似，一般有两种方法：(1)函数法：用其他变量表示该参数，建立函数关系，利用求函数值域的方法求解(2)不等式法：根

9、据题意建立含参数的不等关系式，通过解不等式求参数范围跟踪训练3如图，焦距为2的椭圆E的两个顶点分别为A，B，且与n(，1)共线(1)求椭圆E的标准方程；(2)若直线ykxm与椭圆E有两个不同的交点P和Q，且原点O总在以PQ为直径的圆的内部，求实数m的取值范围解(1)因为2c2，所以c1.又(a，b)，且n，所以ba，所以2b2b21，所以b21，a22.所以椭圆E的标准方程为y21.(2)设P(x1，y1)，Q(x2，y2)，把直线方程ykxm代入椭圆方程y21，消去y，得(2k21)x24kmx2m220，所以x1x2，x1x2.16k28m280，即m22k21.(*)因为原点O总在以PQ

10、为直径的圆的内部，所以0，即x1x2y1y20.又y1y2(kx1m)(kx2m)k2x1x2mk(x1x2)m2.由0，得m2k2.依题意且满足(*)得，m2b0)，M(x，y)为椭圆上的点，由，得a2b.PM2x22324b23(byb)，若b，故矛盾若b，当y时，4b237，b21，a24，所求方程为y21.1已知F1，F2是椭圆1的左、右焦点，弦AB过F1，若ABF2的周长为8，则椭圆的离心率为_答案解析因为ABF2的周长为4a，所以a2，得k2，所以e.2设椭圆1 (mn0)的右焦点与抛物线y28x的焦点相同，离心率为，则此椭圆的方程为_答案1解析y28x的焦点为(2,0)，1的右焦

11、点为(2,0)，c2.又e，m4.c2m2n24，n212.椭圆方程为1.3以抛物线y24x的焦点为顶点，顶点为中心，离心率为2的双曲线的标准方程为_答案x21解析易得抛物线的焦点坐标为(1,0)，所以双曲线的一个顶点坐标为(1,0)设双曲线的标准方程为1(a0，b0)，则a1.又离心率e2，所以c2，从而b2c2a23.所以所求双曲线的标准方程为x21.4若抛物线y22x上的两点A，B到焦点的距离的和是5，则线段AB的中点P到y轴的距离是_答案2解析设l是抛物线的准线，F为抛物线的焦点，A，B，P在l上的投影分别为A1，B1，P1.则由抛物线的定义可知，AA1BB1AFBF5，所以PP1(AA1BB1)，所以点P到y轴的距离为d2.5过椭圆1内一点P(3,1)，且被这点平分的弦所在直线的方程是_答案3x4y130解析设直线与椭圆交于A(x1，y1)，B(x2，y2)两点，由于A，B两点均在椭圆上，故1，1，两式相减得0.又P是A，B的中点，x1x26，y1y22，kAB.直线AB的方程为y1(x3)即3x4y130.在解决圆锥曲线问题时，待定系数法，“设而不求”思想，转化与化归思想是最常用的几种思想方法，“设而不求”思想，在解决直线和圆锥曲线的位置关系问题中匠心独具，很好的解决了计算的繁杂、琐碎问题