2018-2019学年浙江省温州市乐清市育英学校初中分校、育英国际实验学校实验a班八年级（下）期中数学试卷（含详细解答）

《2018-2019学年浙江省温州市乐清市育英学校初中分校、育英国际实验学校实验a班八年级（下）期中数学试卷（含详细解答）》由会员分享，可在线阅读，更多相关《2018-2019学年浙江省温州市乐清市育英学校初中分校、育英国际实验学校实验a班八年级（下）期中数学试卷（含详细解答）（27页珍藏版）》请在七七文库上搜索。

1、2018-2019学年浙江省温州市乐清市育英学校初中分校、育英国际实验学校实验A班八年级（下）期中数学试卷一、选择题（本大题共10小题，每小题4分，共40分，每小题只有一项是符合题目要求的）1（4分）导学案课前预习要求设计4幅既是轴对称又是中心对称的图案，小明设计完成了下列4幅图案，其中符合要求的个数是（）A1个B2个C3个D4个2（4分）2018年俄罗斯世界杯开幕式于6月14日在莫斯科卢日尼基球场举行，该球场可容纳81000名观众，其中数据81000用科学记数法表示为（）A81103B8.1104C8.1105D0.811053（4分）从1、2、3、6这四个数中任取两数，分别记为m、n，那么

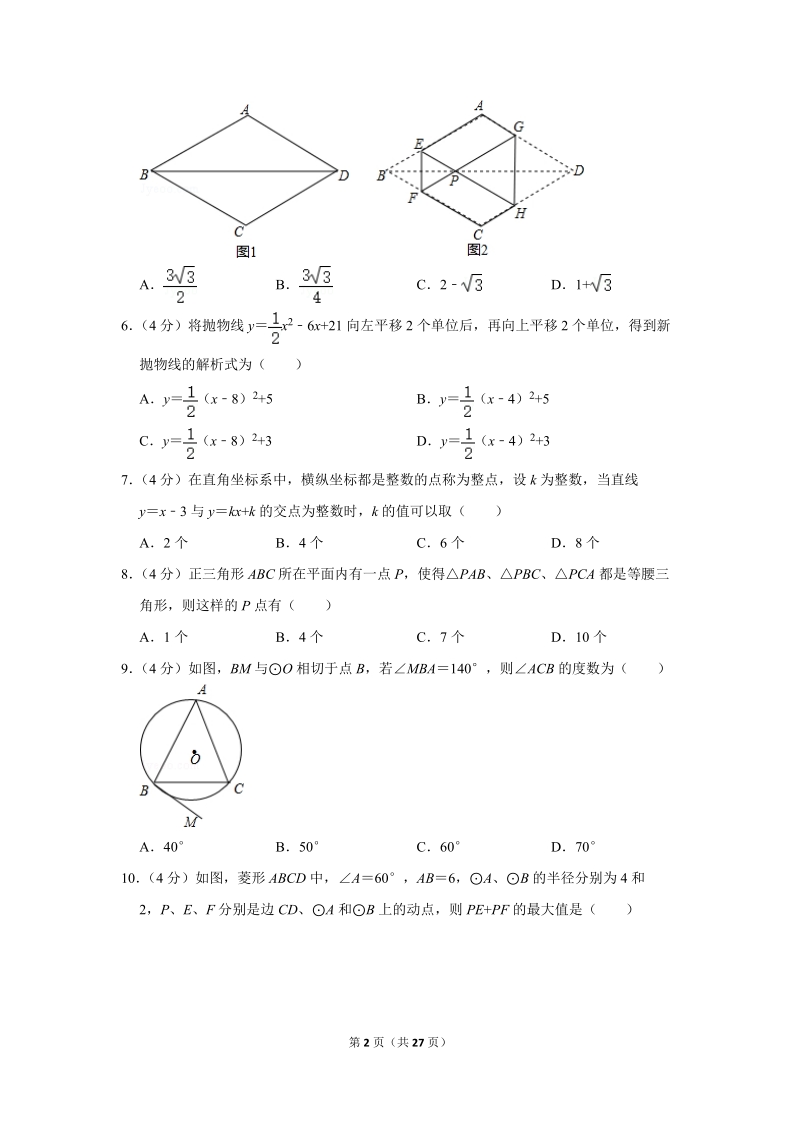
2、点（m，n）在函数y图象的概率是（）ABCD4（4分）如图，将RtABC绕点A按顺时针旋转一定角度得到RtADE，点B的对应点D恰好落在BC边上若AB1，B60，则CD的长为（）A0.5B1.5CD15（4分）如图1，菱形纸片ABCD的边长为2，ABC60，将菱形ABCD沿EF，GH折叠，使得点B，D两点重合于对角线BD上一点P（如图2），则六边形AEFCHG面积的最大值是（）ABC2D1+6（4分）将抛物线yx26x+21向左平移2个单位后，再向上平移2个单位，得到新抛物线的解析式为（）Ay（x8）2+5By（x4）2+5Cy（x8）2+3Dy（x4）2+37（4分）在直角坐标系中，横纵坐标

3、都是整数的点称为整点，设k为整数，当直线yx3与ykx+k的交点为整数时，k的值可以取（）A2个B4个C6个D8个8（4分）正三角形ABC所在平面内有一点P，使得PAB、PBC、PCA都是等腰三角形，则这样的P点有（）A1个B4个C7个D10个9（4分）如图，BM与O相切于点B，若MBA140，则ACB的度数为（）A40B50C60D7010（4分）如图，菱形ABCD中，A60，AB6，A、B的半径分别为4和2，P、E、F分别是边CD、A和B上的动点，则PE+PF的最大值是（）A6+12B6+16C18D6二、填空题（本大题共6小题，每小题5分，共30分）11（5分）多项式x39x因式分解为

4、  12（5分）反比例函数y的图象经过点（tan45，cos60），则k   13（5分）已知RtABC的一边长为10，另两边长恰好是关于x的方程x214x+4k40的两个根，则整数k的值为   14（5分）已知正整数a1，a2a10满足a1a2a10，且以其中任意三个数为边长都不能构成三角形，则的最小值是   15（5分）在锐角三角形ABC中，已知a2，b3，那么第三边c的取值范围是   16（5分）如图，矩形ABCD的顶点A，B在x轴上，且关于y轴对称，反比例函数y（x0）的图象经过点C，反比例函数y（x0）的图象分别与AD，CD交于点E，

5、F，若SBEF7，k1+3k20，则k1等于   三、解答题（本大题共8小题，共80分，解答题因写出文字说明、证明过程或演算步骤）17（8分）（1）计算：（3.14）04cos45（2）解方程：+218（8分）如图，某地下车库的入口处有斜坡CB，长为5m，其坡度i1：2为了行车安全，现将斜坡的坡角改造为15（1）求斜坡的高度（2）求斜坡新起点与原起点之间的距离AB（结果精确到0.1m，参考数据：sin150.259，cos150.966，tan 150.268）19（8分）某市将开展以“走进中国数学史”为主题的知识竞赛活动，红树林学校对本校100名参加选拔赛的同学的成绩按A，B，C，

6、D四个等级进行统计，绘制成如下不完整的统计表和扇形统计图：成绩等级频数（人数）频率A40.04Bm0.51CnD合计1001（1）求m   ，n   ；（2）在扇形统计图中，求“C等级”所对应心角的度数；（3）成绩等级为A的4名同学中有1名男生和3名女生，现从中随机挑选2名同学代表学校参加全市比赛，请用树状图法或者列表法求出恰好选中“1男1女”的概率20（10分）如图，在ABCD中，AEBC，AFCD，垂足分别为E，F，且BEDF（1）求证：ABCD是菱形；（2）若AB5，AC6，求ABCD的面积21（10分）如图，在ABC中，D为边BC上一点，已知，E为AD的中点，延长B

7、E交AC于F，求的值22（12分）如图1，抛物线yax2+（a+2）x+2（a0）与x轴交于点A（4，0），与y轴交于点B，在x轴上有一动点P（m，0）（0m4），过点P作x轴的垂线交直线AB于点N，交抛物线于点M（1）求a的值；（2）若PN：MN1：3，求m的值；（3）如图2，在（2）的条件下，设动点P对应的位置是P1，将线段OP1绕点O逆时针旋转得到OP2，旋转角为（090），连接AP2、BP2，求AP2+BP2的最小值23（10分）某学校为改善办学条件，计划采购A、B两种型号的空调，已知采购3台A型空调和2台B型空调，需费用39000元；4台A型空调比5台B型空调的费用多6000元（1）

8、求A型空调和B型空调每台各需多少元；（2）若学校计划采购A、B两种型号空调共30台，且A型空调的台数不少于B型空调的一半，两种型号空调的采购总费用不超过217000元，该校共有哪几种采购方案？（3）在（2）的条件下，采用哪一种采购方案可使总费用最低，最低费用是多少元？24（14分）如图，点A，B，C，D，E在O上，ABCB于点B，tanD3，BC2，H为CE延长线上一点，且AH，CH5（1）求证：AH是O的切线；（2）若点D是弧CE的中点，且AD交CE于点F，求证：HFHA；（3）在（2）的条件下，求EF的长2018-2019学年浙江省温州市乐清市育英学校初中分校、育英国际实验学校实验A班八年

9、级（下）期中数学试卷参考答案与试题解析一、选择题（本大题共10小题，每小题4分，共40分，每小题只有一项是符合题目要求的）1（4分）导学案课前预习要求设计4幅既是轴对称又是中心对称的图案，小明设计完成了下列4幅图案，其中符合要求的个数是（）A1个B2个C3个D4个【分析】根据轴对称图形与中心对称图形的定义，对每个图形分析、解答【解答】解：第一、二、三个图形既是轴对称图形又是中心对称图形；第四个图形是轴对称图形，不是中心对称图形故选：C【点评】本题主要考查了轴对称图形和中心对称图形，熟记轴对称图形和中心对称图形的定义，是解答本题的基础2（4分）2018年俄罗斯世界杯开幕式于6月14日在莫斯科卢日

10、尼基球场举行，该球场可容纳81000名观众，其中数据81000用科学记数法表示为（）A81103B8.1104C8.1105D0.81105【分析】科学记数法的表示形式为a10n的形式，其中1|a|10，n为整数确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同当原数绝对值1时，n是正数；当原数的绝对值1时，n是负数【解答】解：81000用科学记数法表示为8.1104，故选：B【点评】此题考查科学记数法的表示方法科学记数法的表示形式为a10n的形式，其中1|a|10，n为整数，表示时关键要正确确定a的值以及n的值3（4分）从1、2、3、6这四个数中任取两数，

11、分别记为m、n，那么点（m，n）在函数y图象的概率是（）ABCD【分析】根据反比例函数图象上点的坐标特征可得出mn6，列表找出所有mn的值，根据表格中mn6所占比例即可得出结论【解答】解：点（m，n）在函数y的图象上，mn6列表如下：m111222333666n236136126123mn2362612361861218mn的值为6的概率是故选：B【点评】本题考查了反比例函数图象上点的坐标特征以及列表法与树状图法，通过列表找出mn6的概率是解题的关键4（4分）如图，将RtABC绕点A按顺时针旋转一定角度得到RtADE，点B的对应点D恰好落在BC边上若AB1，B60，则CD的长为（）A0.5B1

12、.5CD1【分析】利用含30度的直角三角形三边的关系得到BC2AB2，再根据旋转的性质得ADAB，则可判断ABD为等边三角形，所以BDAB1，然后计算BCBD即可【解答】解：BAC90，B60，BC2AB2，RtABC绕点A按顺时针旋转一定角度得到RtADE，点B的对应点D恰好落在BC边上，ADAB，而B60，ABD为等边三角形，BDAB1，CDBCBD211故选：D【点评】本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等5（4分）如图1，菱形纸片ABCD的边长为2，ABC60，将菱形ABCD沿EF，GH折叠，使得点B，D两点重合

13、于对角线BD上一点P（如图2），则六边形AEFCHG面积的最大值是（）ABC2D1+【分析】由六边形AEFCHG面积菱形ABCD的面积EBF的面积GDH的面积得出函数关系式，进而求出最大值【解答】解：六边形AEFCHG面积菱形ABCD的面积EBF的面积GDH的面积菱形纸片ABCD的边长为2，ABC60，AC2，BD2，S菱形ABCDACBD222，设AEx，则六边形AEFCHG面积2（2x）（2x）xxx2+x+（x1）2+，六边形AEFCHG面积的最大值是故选：A【点评】考查了翻折变换（折叠问题），二次函数最值问题，本题关键是设出未知数表示六边形面积，把图形问题转化为函数问题，有一定的难度6

14、（4分）将抛物线yx26x+21向左平移2个单位后，再向上平移2个单位，得到新抛物线的解析式为（）Ay（x8）2+5By（x4）2+5Cy（x8）2+3Dy（x4）2+3【分析】根据平移规律得到平移后抛物线的顶点坐标，根据该顶点坐标写出新抛物线解析式即可【解答】解：抛物线yx26x+21（x6）2+3，它的顶点坐标是（6，3）将其向左平移2个单位，再向上平移2个单位后，得到新抛物线的顶点坐标是（4，5），所以新抛物线的解析式是：y（x4）2+5故选：B【点评】本题考查了二次函数与几何变换：由于抛物线平移后的形状不变，故a不变，所以求平移后的抛物线解析式通常可利用两种方法：一是求出原抛物线上任意

15、两点平移后的坐标，利用待定系数法求出解析式；二是只考虑平移后的顶点坐标，即可求出解析式7（4分）在直角坐标系中，横纵坐标都是整数的点称为整点，设k为整数，当直线yx3与ykx+k的交点为整数时，k的值可以取（）A2个B4个C6个D8个【分析】让这两条直线的解析式组成方程组，求得整数解即可【解答】解：由题意得：，解得：，交点为整数，k可取的整数解有0，2，3，5，1，3共6个故选：C【点评】本题考查了两条直线相交或者平行问题，难度一般，解决本题的难点是根据分数的形式得到相应的整数解8（4分）正三角形ABC所在平面内有一点P，使得PAB、PBC、PCA都是等腰三角形，则这样的P点有（）A1个B4个

16、C7个D10个【分析】（1）点P在三角形的内部时，点P到ABC的三个顶点的距离相等，所以点P是三角形的外心；（2）点P在三角形的外部时，每条边的垂直平分线上的点只要能够使顶点这条边的两端点连接而成的三角形是等腰三角形即可【解答】解：（1）点P在三角形内部时，点P是边AB、BC、CA的垂直平分线的交点，是三角形的外心；（2）分别以三角形各顶点为圆心，边长为半径，交垂直平分线的交点就是满足要求的每条垂直平分线上得3个交点，再加三角形的垂心，一共10个故选：D【点评】本题主要考查等腰三角形的性质；要注意分点在三角形内部和三角形外部两种情况讨论，思考全面是正确解答本题的关键9（4分）如图，BM与O相切

17、于点B，若MBA140，则ACB的度数为（）A40B50C60D70【分析】连接OA、OB，由切线的性质知OBM90，从而得ABOBAO50，由内角和定理知AOB80，根据圆周角定理可得答案【解答】解：如图，连接OA、OB，BM是O的切线，OBM90，MBA140，ABO50，OAOB，ABOBAO50，AOB80，ACBAOB40，故选：A【点评】本题主要考查切线的性质，解题的关键是掌握切线的性质：圆的切线垂直于经过切点的半径经过圆心且垂直于切线的直线必经过切点经过切点且垂直于切线的直线必经过圆心10（4分）如图，菱形ABCD中，A60，AB6，A、B的半径分别为4和2，P、E、F分别是边C

18、D、A和B上的动点，则PE+PF的最大值是（）A6+12B6+16C18D6【分析】如图，连接PB，延长PB交B于F，连接PA交A于E，要求PE+PF的最大值，可以转化为求PA+PB的最大值通过寻找特殊点，发现当点P与点C重合时，PA、PB同时取得最大值，此时PA+PB的值最大【解答】解：如图，连接PB，延长PB交B于F，连接PA交A于E，要求PE+PF的最大值，可以转化为求PA+PB的最大值点P在线段CD上，当点P与点C重合时，PA最大，（因为ACDADC，所以，点C是“小角”点）；当点P与点C或者点D重合时，PB最大（因为ACDADC，所以，点C、D均是“小角”点）所以，根据、可知，当点P

19、与点C重合时，PA、PB同时取得最大值，此时PA+PB的值最大，在ACD中，ADC120，ADDC6，AC266，PE+PF的最大值AC+AE+BC+BF6+12故选：A【点评】本题考查菱形的性质、等边三角形的性质，点与圆的位置关系等知识，解题的关键是理解题意，正确寻找使得PE+PF的值最大时的位置，属于中考常考题型二、填空题（本大题共6小题，每小题5分，共30分）11（5分）多项式x39x因式分解为x（x+3）（x3）【分析】原式提取x，再利用平方差公式分解即可【解答】解：原式x（x29）x（x+3）（x3），故答案为：x（x+3）（x3）【点评】此题考查了提公因式法与公式法的综合运用，熟练

20、掌握因式分解的方法是解本题的关键12（5分）反比例函数y的图象经过点（tan45，cos60），则k【分析】先求得该点的坐标，然后代入反比例函数解析式即可求得k的值【解答】解：tan451，cos60，ktan45cos60【点评】函数解析式上的点的坐标适合这个函数解析式13（5分）已知RtABC的一边长为10，另两边长恰好是关于x的方程x214x+4k40的两个根，则整数k的值为13【分析】根据勾股定理，以及一元二次方程中根与系数的关系即可解答不过要分10是斜边和直角边两种情况进行讨论【解答】解：RtABC的一边长为10，另两边长恰好是关于x的方程x214x+4k40的两个根，设为、（1）边

21、长为10的边是斜边，有2+2（+）221422（4k4）100求得k13（2）已知边为直角边，有22（+）（）14（）1414100解得k50为分数故舍去【点评】本题考查一元二次方程根与系数的关系，理解对方程的两边进行讨论是解决本题的关键14（5分）已知正整数a1，a2a10满足a1a2a10，且以其中任意三个数为边长都不能构成三角形，则的最小值是55【分析】根据三角形的特征：任意两边之和大于第三边，任意两边之差小于第三边；由此解答即可【解答】解：因为三角形任意两边之和大于第三边，任意两边之差小于第三边，正整数a1，a2a10满足a1a2a10设最短的一条长1，则第二条线段长为1，所以只要满足

22、任意两条线段之和等于下一个数字即可，此时最长的线段也最短，1+122+133+255+388+51313+821，21+1334，34+2155，即这10条线段为：1，1，2，3，5，8，13，21，34，55任意三条都不能作为边构成三角形，所以的最小值为55，故答案为55【点评】此题主要考查了三角形三边关系，解答关键是根据三角形中任意两边之和大于第三边的特征解决问题15（5分）在锐角三角形ABC中，已知a2，b3，那么第三边c的取值范围是c【分析】题中已知ABC是锐角三角形，没有指明哪个角是最大角，从而无法确定边之间的关系，从而可以分两种情况进行分析，从而确定第三边c的变化范围【解答】解：当

23、C是最大角时，有C90，c，c，当B是最大角时，有B90b2a2+c294+c2c，第三边c的变化范围：c，故答案为：c【点评】考查了三角形三边关系，此类求三角形第三边的范围的题，实际上就是根据三角形三边关系定理列出不等式，然后解不等式即可16（5分）如图，矩形ABCD的顶点A，B在x轴上，且关于y轴对称，反比例函数y（x0）的图象经过点C，反比例函数y（x0）的图象分别与AD，CD交于点E，F，若SBEF7，k1+3k20，则k1等于9【分析】设出点A坐标，根据函数关系式分别表示各点坐标，根据割补法表示BEF的面积，构造方程【解答】解：设点B的坐标为（a，0），则A点坐标为（a，0）由图象可

24、知，点C（a，），E（a，），D（a，），F（，）矩形ABCD面积为：2a2k1SDEFSBCFSABESBEF72k1+k27    k1+3k20k2k1代入式得解得k19故答案为：9【点评】本题是反比例函数综合题，解题关键是设出点坐标表示相关各点，应用面积法构造方程三、解答题（本大题共8小题，共80分，解答题因写出文字说明、证明过程或演算步骤）17（8分）（1）计算：（3.14）04cos45（2）解方程：+2【分析】（1）原式利用二次根式性质，零指数幂法则，以及特殊角的三角函数值计算即可求出值；（2）分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即

25、可得到分式方程的解【解答】解：（1）原式2121；（2）去分母：x+2（x2）1，去括号：x+2x41，x1，经检验：x1是原方程的解【点评】此题考查了解分式方程，利用了转化的思想，解分式方程注意要检验18（8分）如图，某地下车库的入口处有斜坡CB，长为5m，其坡度i1：2为了行车安全，现将斜坡的坡角改造为15（1）求斜坡的高度（2）求斜坡新起点与原起点之间的距离AB（结果精确到0.1m，参考数据：sin150.259，cos150.966，tan 150.268）【分析】（1）由于在RtABC中，斜坡CB长为5m，其坡度i1：2，利用勾股定理即可求解；（2）利用（1）中CD的长度和现在的坡度

26、即可求出线段AD的长度，然后减去DB的长度即可解决问题【解答】解：（1）在RtABC中，斜坡CB长为5m，其坡度i1：2，BD2CD，又BC2CD2+BD2，755CD2，CD5m，BD10m；（2）在RtACD中，CD5m，CAD15，AD18.66m，ABADBD18.66108.668.7m【点评】此题主要考查了解直角三角形的应用坡角坡度的问题，解题的关键是首先正确理解题意，然后利用三角函数即可解决问题19（8分）某市将开展以“走进中国数学史”为主题的知识竞赛活动，红树林学校对本校100名参加选拔赛的同学的成绩按A，B，C，D四个等级进行统计，绘制成如下不完整的统计表和扇形统计图：成绩等

27、级频数（人数）频率A40.04Bm0.51CnD合计1001（1）求m51，n30；（2）在扇形统计图中，求“C等级”所对应心角的度数；（3）成绩等级为A的4名同学中有1名男生和3名女生，现从中随机挑选2名同学代表学校参加全市比赛，请用树状图法或者列表法求出恰好选中“1男1女”的概率【分析】（1）由A的人数和其所占的百分比即可求出总人数，由此即可解决问题；（2）由总人数求出C等级人数，根据其占被调查人数的百分比可求出其所对应扇形的圆心角的度数；（3）列表得出所有等可能的情况数，找出刚好抽到一男一女的情况数，即可求出所求的概率；【解答】解：（1）参加本次比赛的学生有：40.04100（人）；m0

28、.5110051（人），D组人数10015%15（人），n1004511530（人）故答案为51，30；（2）B等级的学生共有：504208216（人）所占的百分比为：165032%C等级所对应扇形的圆心角度数为：36030%108（3）列表如下：男女1女2女3男（女，男）（女，男）（女，男）女1（男，女）（女，女）（女，女）女2（男，女）（女，女）（女，女）女3（男，女）（女，女）（女，女）共有12种等可能的结果，选中1名男生和1名女生结果的有6种P（选中1名男生和1名女生）【点评】此题考查了列表法与树状图法，用到的知识点为：概率所求情况数与总情况数之比20（10分）如图，在ABCD中，AE

29、BC，AFCD，垂足分别为E，F，且BEDF（1）求证：ABCD是菱形；（2）若AB5，AC6，求ABCD的面积【分析】（1）利用全等三角形的性质证明ABAD即可解决问题；（2）连接BD交AC于O，利用勾股定理求出对角线的长即可解决问题；【解答】（1）证明：四边形ABCD是平行四边形，BD，AEBC，AFCD，AEBAFD90，BEDF，AEBAFDABAD，四边形ABCD是菱形（2）连接BD交AC于O四边形ABCD是菱形，AC6，ACBD，AOOCAC63，AB5，AO3，BO4，BD2BO8，S平行四边形ABCDACBD24【点评】本题考查菱形的判定和性质、勾股定理、全等三角形的判定和性质

30、等知识，解题的关键是正确寻找全等三角形解决问题，属于中考常考题型21（10分）如图，在ABC中，D为边BC上一点，已知，E为AD的中点，延长BE交AC于F，求的值【分析】过D作DGAC，可得AEFDEG，即DGAF，再由平行线的性质可得对应线段成比例，进而即可求解AF与AC的比值【解答】解：过D作DGAC交BF于G，E是AD的中点，AEFDEG，DGAF，DGAC，BD：DC5：3，DG：CF5：8，AF：CF5：8，AF：AC5：13【点评】本题主要考查了全等三角形的判定及性质以及平行线分线段成比例的性质问题，能够熟练掌握22（12分）如图1，抛物线yax2+（a+2）x+2（a0）与x轴交

31、于点A（4，0），与y轴交于点B，在x轴上有一动点P（m，0）（0m4），过点P作x轴的垂线交直线AB于点N，交抛物线于点M（1）求a的值；（2）若PN：MN1：3，求m的值；（3）如图2，在（2）的条件下，设动点P对应的位置是P1，将线段OP1绕点O逆时针旋转得到OP2，旋转角为（090），连接AP2、BP2，求AP2+BP2的最小值【分析】（1）把A点坐标代入可得到关于a的方程，可求得a的值；（2）由OABPAN可用m表示出PN，且可表示出PM，由条件可得到关于m的方程，则可求得m的值；（3）在y轴上取一点Q，使，可证得P2OBQOP2，则可求得Q点坐标，则可把AP2+BP2化为AP2+Q

32、P2，利用三角形三边关系可知当A、P2、Q三点在一条线上时有最小值，则可求得答案【解答】解：（1）A（4，0）在抛物线上，016a+4（a+2）+2，解得a；（2）由（1）可知抛物线解析式为yx2+x+2，令x0可得y2，OB2，OPm，AP4m，PMx轴，OABPAN，即，PN（4m），M在抛物线上，PMm2+m+2，PN：MN1：3，PN：PM1：4，m2+m+24（4m），解得m3或m4（舍去）；（3）在y轴上取一点Q，使，如图，由（2）可知P1（3，0），且OB2，且P2OBQOP2，P2OBQOP2，当Q（0，）时QP2BP2，AP2+BP2AP2+QP2AQ，当A、P2、Q三点在一

33、条线上时，AP2+QP2有最小值，A（4，0），Q（0，），AQ，即AP2+BP2的最小值为【点评】本题为二次函数的综合应用，涉及待定系数法、相似三角形的判定和性质、勾股定理、三角形三边关系等知识在（2）中用m分别表示出PN和PM是解题的关键，在（3）确定出取得最小值时的位置是解题的关键本题考查知识点较多，综合性较强，特别是（3）中构造三角形相似，难度较大23（10分）某学校为改善办学条件，计划采购A、B两种型号的空调，已知采购3台A型空调和2台B型空调，需费用39000元；4台A型空调比5台B型空调的费用多6000元（1）求A型空调和B型空调每台各需多少元；（2）若学校计划采购A、B两种型号

34、空调共30台，且A型空调的台数不少于B型空调的一半，两种型号空调的采购总费用不超过217000元，该校共有哪几种采购方案？（3）在（2）的条件下，采用哪一种采购方案可使总费用最低，最低费用是多少元？【分析】（1）根据题意可以列出相应的方程组，从而可以解答本题；（2）根据题意可以列出相应的不等式组，从而可以求得有几种采购方案；（3）根据题意和（2）中的结果，可以解答本题【解答】解：（1）设A型空调和B型空调每台各需x元、y元，解得，答：A型空调和B型空调每台各需9000元、6000元；（2）设购买A型空调a台，则购买B型空调（30a）台，解得，10a12，a10、11、12，共有三种采购方案，方

35、案一：采购A型空调10台，B型空调20台，方案二：采购A型空调11台，B型空调19台，方案三：采购A型空调12台，B型空调18台；（3）设总费用为w元，w9000a+6000（30a）3000a+180000，当a10时，w取得最小值，此时w210000，即采购A型空调10台，B型空调20台可使总费用最低，最低费用是210000元【点评】本题考查一次函数的应用、一元一次不等式组的应用、二元一次方程组的应用，解答本题的关键是明确题意，找出所求问题需要的条件，利用函数和不等式的思想解答24（14分）如图，点A，B，C，D，E在O上，ABCB于点B，tanD3，BC2，H为CE延长线上一点，且AH，

36、CH5（1）求证：AH是O的切线；（2）若点D是弧CE的中点，且AD交CE于点F，求证：HFHA；（3）在（2）的条件下，求EF的长【分析】（1）连接AC由ABBC可知AC是圆O的直径，由同弧所对的圆周角相等可知CD，于是得到tanC3，故此可知AB6，在RtABC中，由勾股定理得：AC240，从而可得到AC2+AH2CH2，由勾股定理的逆定理可知ACAH，故此可知AH是圆O的切线；（2）连接DE、BE由弦切角定理可知ABDHAD，由D是的中点，可证明CEDEBD，由同弧所对的圆周角相等可知ABEADE，结合三角形的外角的性质可证明：HAFAFH，故此AHHF；（3）由切割线定理可求得EH，由

37、（2）可知AFFH，从而得到EFFHEH【解答】解：（1）如图1所示：连接ACABCB，AC是圆O的直径CD，tanC3AB3BC326在RtABC中，由勾股定理得：AC2AB2+BC240又AH210，CH250，AC2+AH2CH2ACH为直角三角形ACAHAH是圆O的切线（2）如图2所示：连接DE、BEAH是圆O的切线，ABDHADD是的中点，CEDEBD又ABEADE，ABE+EBDADE+CEDABDAFEHAFAFHAHHF（3）由切割线定理可知：AH2EHCH，即（）25EH解得：EH由（2）可知AFFHEFFHEH【点评】本题主要考查的是圆的综合应用，解答本题主要应用了切线的判定定理、弦切角定理、切割线定理、圆周角定理以及勾股定理和勾股定理的逆定理、三角形的外角的性质，掌握本题的辅助线的作法是解题的关键