2020中考数学 专题训练-与圆相关的面积和长度计算（解析版）

《2020中考数学 专题训练-与圆相关的面积和长度计算（解析版）》由会员分享，可在线阅读，更多相关《2020中考数学 专题训练-与圆相关的面积和长度计算（解析版）（9页珍藏版）》请在七七文库上搜索。

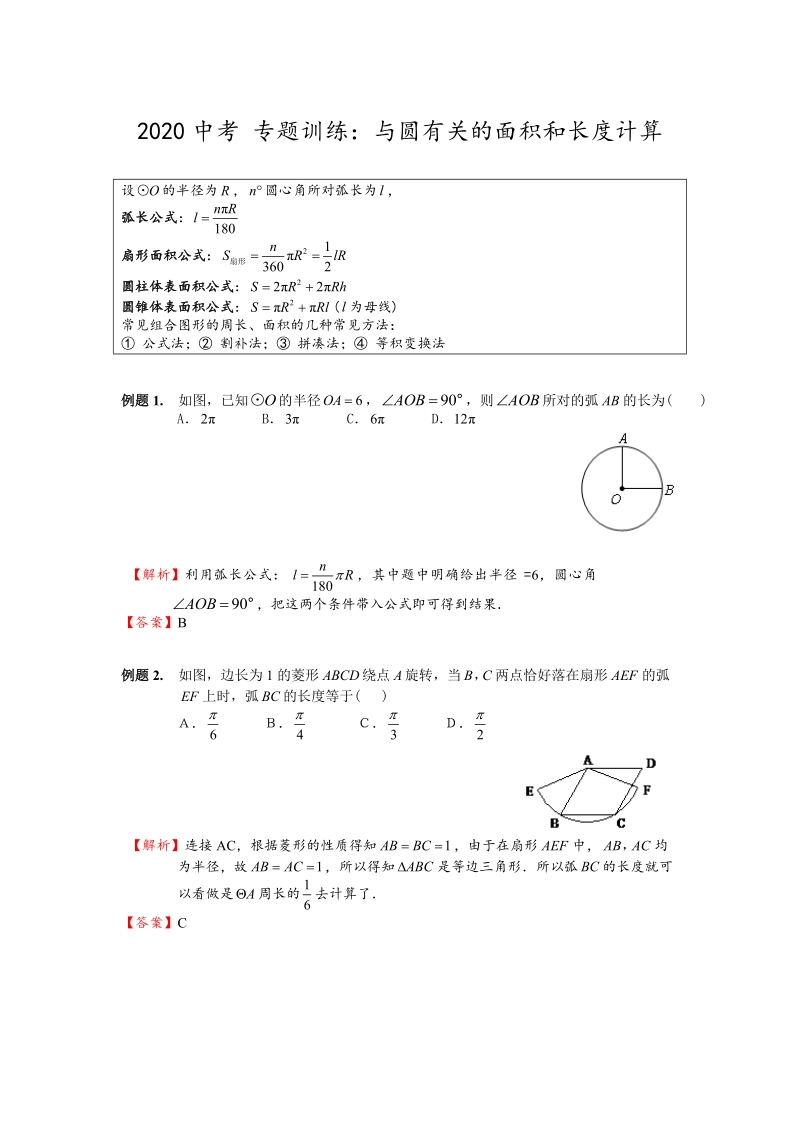
1、2020中考 专题训练：与圆有关的面积和长度计算设的半径为，圆心角所对弧长为，弧长公式：扇形面积公式：圆柱体表面积公式：圆锥体表面积公式：(为母线)常见组合图形的周长、面积的几种常见方法： 公式法； 割补法； 拼凑法； 等积变换法例题1. 如图，已知的半径，则所对的弧的长为( )ABCD 【解析】利用弧长公式：，其中题中明确给出半径=6，圆心角，把这两个条件带入公式即可得到结果【答案】B例题2. 如图，边长为1的菱形绕点旋转，当两点恰好落在扇形的弧上时，弧的长度等于( ) 【解析】连接AC，根据菱形的性质得知，由于在扇形中，均为半径，故，所以得知是等边三角形所以弧的长度就可以看做是周长的去计算

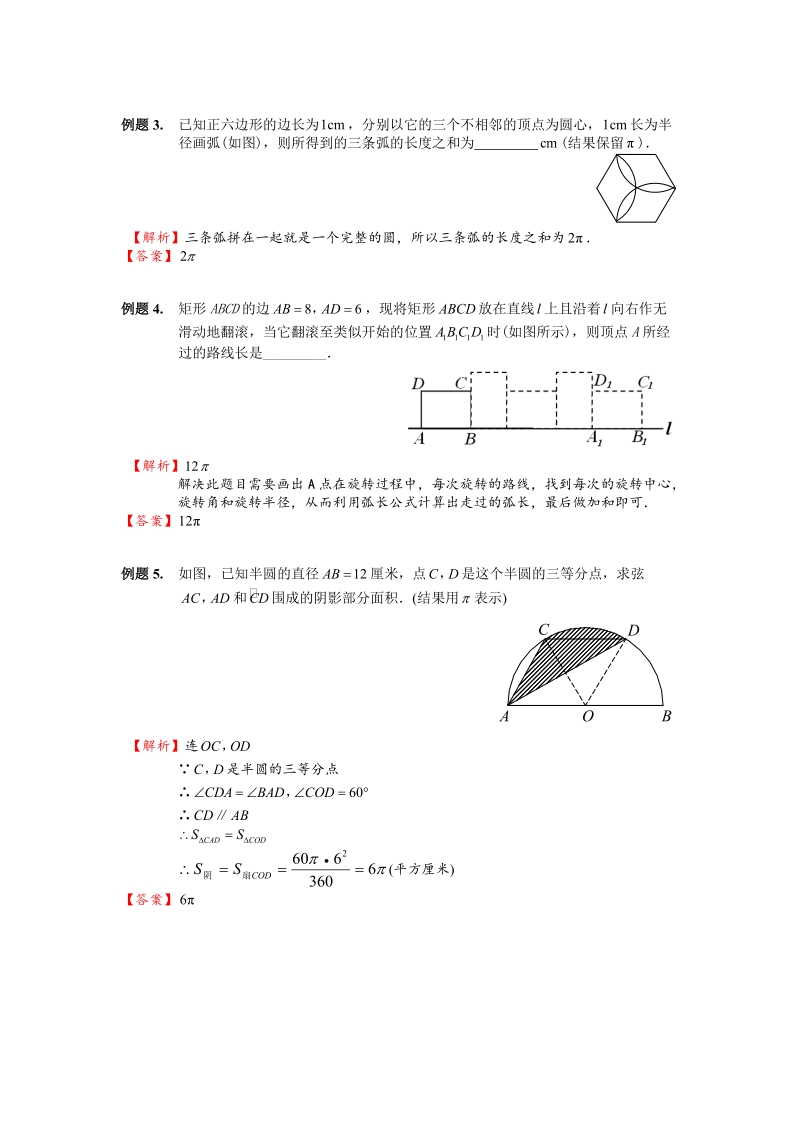
2、了【答案】C例题3. 已知正六边形的边长为，分别以它的三个不相邻的顶点为圆心，长为半径画弧(如图)，则所得到的三条弧的长度之和为 (结果保留) 【解析】三条弧拼在一起就是一个完整的圆，所以三条弧的长度之和为【答案】例题4. 矩形ABCD的边，现将矩形放在直线上且沿着向右作无滑动地翻滚，当它翻滚至类似开始的位置时(如图所示)，则顶点A所经过的路线长是_ 【解析】12解决此题目需要画出A点在旋转过程中，每次旋转的路线，找到每次的旋转中心，旋转角和旋转半径，从而利用弧长公式计算出走过的弧长，最后做加和即可【答案】例题5. 如图，已知半圆的直径厘米，点是这个半圆的三等分点，求弦和围成的阴影部分面积(结

3、果用表示) 【解析】连是半圆的三等分点(平方厘米)【答案】例题6. 将绕点逆时针旋转到使在同一直线上，若，则图中阴影部分面积为 cm2 【解析】3此题需要把所在的圆补充完整，设它与线段的交点为，与的交点为从而看出整个阴影部分可以割补成扇形的面积-扇形的面积即【答案】例题7. 如图，圆心角都是的扇形与扇形叠放在一起，连结(1)求证：；(2)若图中阴影部分的面积是，求的长 【解析】根据题意结合图形可知：，得出与全等，从而得到(2)1cm根据旋转以及图形的割补可知图中阴影部分面积=扇形的面积-扇形的面积，带入公式，即可得到的长度1cm【答案】见解析例题8. 如图，在半径为，圆心角等于的扇形内部作一个

4、正方形，使点在上，点在上，点在上，则阴影部分的面积为_ 【解析】连结，由勾股定理可计算得正方形的边长为，则正方形的面积为，等腰直角三角形的面积为，扇形的面积为，所以阴影部分的面积为【答案】例题9. 如图，已知点均在已知圆上，平分，四边形的周长为图中阴影部分的面积为_ 【解析】省略【答案】例题10. 如果矩形纸片的两条邻边分别为和，将其围成一个圆柱的侧面，求圆柱的底面半径 【解析】如果将长为的边转化成圆柱的底面周长，设底面半径为，则，所以底面半径；如果将长为的边转化成圆柱的底面周长，设底面半径为，则，所以底面半径故这个圆柱的底面半径为或【答案】或例题11. 圆柱的侧面展开图是一个矩形，如右图所示

5、，对角线，求圆柱的底面积 【解析】设圆柱的底面半径为 为母线长，则为底面圆的周长， 为母线，则为底面圆的周长，故圆柱的底面积为或【答案】或例题12. 如图已知扇形的半径为6cm，圆心角的度数为，若将此扇形围成一个圆锥，则围成的圆锥的侧面积为()A B C D 【解析】此题考查的是扇形的面积公式：，把题中的已知条件带入求解即可【答案】D例题13. 某个圆锥的侧面展开图形是一个半径为，圆心角为的扇形，则这个圆锥的底面半径为_ 【解析】省略【答案】例题14. 如果圆锥的底面半径是，母线长是，那么这个圆锥侧面展开图圆心角的度数是_ 【解析】圆锥侧面展开图的扇形弧长为，设圆心角的度数为，则，【答案】例题

6、15. 圆锥的底面半径为8，母线长为9，则该圆锥的侧面积为()A B C D 【解析】此题考查的是弧长公式以及扇形面积公式的掌握，但之前需要根据已知条件求出圆锥侧面展开图的圆心角，通过圆锥的底面圆周长与展开图的弧长之间的关系即：然后利用扇形的面积公式计算即可【答案】D例题16. 若一个圆锥的底面积是侧面积的，则该圆锥侧面展开图的圆心角度数是_ _度 【解析】省略【答案】例题17. 一个圆锥的侧面展开图是一个半圆，则此圆锥母线长与底面半径之比为_ 【解析】省略【答案】例题18. 小华为参加毕业晚会演出，准备制作一顶圆锥形纸帽，纸帽的底面半径为，母线长为，制作这个纸帽需要纸板的面积至少为 (结果保

7、留) 【解析】需要纸板的面积即圆锥的侧面积，又圆锥侧面积，制作这个纸帽需要纸板的面积至少为【答案】例题19. 如图，小明从半径为5的圆形纸片中剪下40%圆周的一个扇形，然后利用剪下的扇形制作成一个圆锥形玩具纸帽(接缝处不重叠)，那么这个圆锥的高为( )A3 B4 C D 【解析】此题需要学生熟练掌握弧长公式，并了解弧长即为所围成圆锥的底面圆的周长即，得到底面圆的半径，最后在圆锥的截面图中得知：所求圆锥的高即为直角三角形的斜边，再利用勾股定理即可得到【答案】C例题20. 圆锥的母线长是，底面半径长是，是底面圆周上一点，则从点出发绕侧面一周，再回到点的最短路线长是_ 【解析】【答案】例题21. 已

8、知为圆锥的顶点，为圆锥底面上一点，点在上一只蜗牛从点出发，绕圆锥侧面爬行，回到点时所爬过的最短路线的痕迹如右图所示若沿将圆锥侧面剪开并展开，所得侧面展开图是( ) 【解析】解决此题的关键是要把立体图形转变成平面图形把圆锥的侧面展开图扇形画出来，然后根据点从圆锥的侧面环绕一周回到点可以知道，反映在扇形上就是在半径上点对称到半径上的水平距离【答案】D例题22. 如图是一个用来盛爆米花的圆锥形纸杯，纸杯开口圆的直径长为10cm母线长为10cm在母线上的点处有一块爆米花残渣，且cm，一只蚂蚁从杯口的点处沿圆锥表面爬行到点则此蚂蚁爬行的最短距离为 cm 【解析】要把立体图形还原成符合题意的平面图形，然后

9、根据题中所给条件把已知线段标注在图中，从而利用特殊图形，如：直角三角形计算所求线段长【答案】例题23. 已知在中，把绕直线旋转一周得到一个圆锥，其表面积为，把绕直线旋转一周得到另一个圆锥，其表面积为，则：等于_ 【解析】此题的关键是要把两个圆锥找准确，其中绕直线旋转得到的圆锥是以为母线，底面圆半径为6，侧面展开图的圆心角为，它的表面积；而绕旋转得到的图形是两个圆锥扣在一起的形式，上面的圆锥的母线为，底面圆半径为斜边上的高，下面的圆锥的母线为，底面圆半径也是，故通过计算可得【答案】例题24. 在手工课上甲、乙两名同学合作，将半径为1米，圆心角为90的扇形薄铁片围成一个圆锥筒，在计算圆锥的容积时(

10、接缝忽略不计)，甲认为圆锥的高就等于扇形的圆心到弦的距离(如图)，乙说这样计算不正确，你同意谁的说法？把正确的计算过程写出来 【解析】在图(1)中，因为在图(2)中，的周长等于图(1)中的长所以，所以，故：甲的说法不正确【答案】甲说的不正确例题25. 半径为的弧长等于半径为的圆周长，则这条弧所对的圆心角的度数是_ 【解析】设弧所对圆心角的度数为，则， 【答案】例题26. 若一扇形的弧长为，圆心角为，则扇形的面积为_ 【解析】设扇形的半径为，则， 【答案】例题27. 一个扇形的半径为，圆心角为，若用它做成一个圆锥的侧面，则这个圆锥的底面半径为_ 【解析】扇形的弧长，它作为圆锥的底面周长 ，【答案】例题28. 如图，在中，若以为直径的圆交 于点，则阴影部分的面积是_ 【解析】连结 是圆的直径， 是等腰直角三角形，是中点， ， 根据圆的对称性，阴影部分的面积=【答案】例题29. 设矩形的长与宽的和为，以为轴心旋转一周得到一个几何体，则此几何体的侧面积有( )A最小值B最大值 C最大值D最小值学科网 【解析】省略【答案】C