2020年中考二轮数学培优专题：几何最值问题（含答案）

《2020年中考二轮数学培优专题：几何最值问题（含答案）》由会员分享，可在线阅读，更多相关《2020年中考二轮数学培优专题：几何最值问题（含答案）（9页珍藏版）》请在七七文库上搜索。

1、2020中考数学培优专题：几何最值问题（含答案） 1.如图，已知圆柱底面的周长为4dm，圆柱高为2dm，在圆柱的侧面上，过点A和点C嵌有一圈金属丝，则这圈金属丝的周长最小为( )A4dm B2dm C2dm D4dm2.如图，ABC的面积等于6，边AC=3.现将ABC沿AB所在直线翻折，使点C落在直线AD上的C处。点P在直线AD上，则线段BP的长不可能是（）A.3B.4C.5D.6ABC3.如图是一个三级台阶，它的每一级的长、宽和高分别是50 cm，30 cm，10 cm，A和B是这个台阶的两个相对的端点，A点上有一只壁虎，它想到B点去吃可口的食物，请你想一想，这只壁虎从A点出发，沿着台阶面爬

2、到B点，至少需爬()A13 cm B40 cm C130 cm D169 cm4.如图，已知直线ab，且a与b之间的距离为4，点A到直线a的距离为2，点B到直线b的距离为3，AB=。试在直线a上找一点M，在直线b上找一点N，满足MNa且AM+MN+NB的长度和最短，则此时AM+NB=( )A6 B8 C10 D125.一盛满水的圆柱形容器,它的高等于80厘米,底面半径等于30厘米,在圆柱下底面上的A点有一条小鱼,它想从点A游到点B , 小鱼游过的最短路程是 6.如图，长方体的底面边长分别为2cm和4cm，高为5cm。若一只蚂蚁从P点开始经过4个侧面爬行一圈到达Q点，则蚂蚁爬行的最短路径长为 c

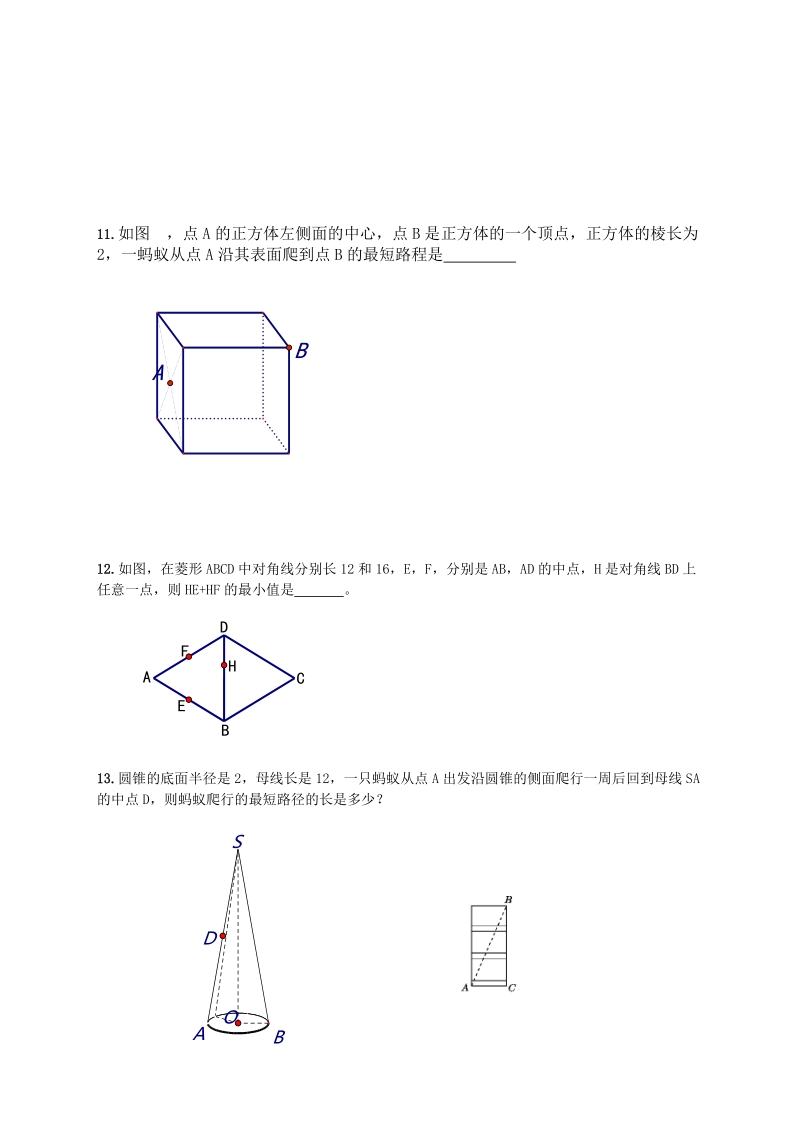
3、m7.如图所示，一圆柱高8cm，底面半径2cm，一只蚂蚁从点A爬到点B处吃食，要爬行的最短路程是 （取3）8.如图，长方体的长为15，宽为10，高为20，点B离点C的距离为5，一只蚂蚁如果要沿着长方体的表面从点A爬到点B，需要爬行的最短距离是 。9.已知菱形ABCD的两条对角线长分别为6和8，M、N分别是边BC、CD的中点，P是对角线上BD上一点，则PM+PN的最小值是 .10.若圆的半径2cm，圆中一条弦AB长1cm，点P是劣弧AB上的一个动点，则点P到弦AB的最大距离是 11.如图 ，点A的正方体左侧面的中心，点B是正方体的一个顶点，正方体的棱长为2，一蚂蚁从点A沿其表面爬到点B的最短路程

4、是 12.如图，在菱形ABCD中对角线分别长12和16，E，F，分别是AB，AD的中点，H是对角线BD上任意一点，则HE+HF的最小值是 。13.圆锥的底面半径是2，母线长是12，一只蚂蚁从点A出发沿圆锥的侧面爬行一周后回到母线SA的中点D，则蚂蚁爬行的最短路径的长是多少？参考答案一、单选题（共有4道小题）1.A2.A3.C解析：将台阶面展开，连接AB，如图，线段AB即为壁虎所爬的最短路线因为BC303103120(cm)，AC50 cm，在RtABC中，根据勾股定理，得16900，所以AB130 cm.所以壁虎至少爬行130 cm.4.B二、填空题（共有8道小题）5.1006.137.108

5、.259.510.11.12.10三、解答题（共有1道小题）13.解；如图，将圆锥沿SA剪开并展开其侧面，则题目中要求的最短路径即为AD可求得在扇形SAA中，若假设ASA=n则，可求得ASA=n=60又SA=SA，ASA是等边三角形又D为AS的中点，ADDAS=30DS=6在RtDSA中由勾股定理可得，即最短路径为几何最值-练习二1.如图，已知线段OA交O于点B，且OB=AB，点P是O上的一个动点，那么OAP的最大值是（）A30B45C60D902.如图所示，已知为反比例函数图象上的两点，动点在x轴的正半轴上运动，当线段AP与线段BP之差达到最大时，点P的坐标是（）A. B.C. D.3.如图

6、是一个三级台阶，它的每一级的长宽和高分别为20dm、3dm、2dm，A和B是这个台阶两个相对的端点，A点有一只蚂蚁，想到B点去吃可口的食物，则蚂蚁沿着台阶面爬到B点最短路程是 4.如图，正方形ABCD的边长为2，点E为边BC的中点，点P在对角线BD上移动，则PE+PC的最小值是 5.有一个圆柱,它的高等于12厘米,底面半径等于3厘米,在圆柱下底面上的A点有一只蚂蚁,它想从点A爬到点B , 蚂蚁沿着圆柱表面爬行的最短路程是 （取近似值3）6.如图，在RtAOB中，OA=OB=,O的半径为1，点P是AB边上的动点，过点P作O的一条切线PQ（点Q为切点），则切线长PQ的最小值为 。7.如图，边长为1

7、的正方体中，一只蚂蚁从顶点A出发沿着正方体的外表面爬到顶点B的最短距离是 8.如图所示，在锐角ABC中，AB=4，BAC=45，BAC的平分线交BC于点D，M、N分别是AD和AB上的动点，则BM+MN的最小值是 9.如图，已知抛物线的顶点为A（1，4）、抛物线与y轴交于点B（0，3），与x轴交于C、D两点。点P是x轴上的一个动点.（1）求此抛物线的解析式. （2）当PA+PB的值最小时，求点P的坐标 10.圆锥的底面半径是2，母线长是12，一只蚂蚁从点B出发沿圆锥的侧面爬行一周后回到B点，则蚂蚁爬行的最短路径的长是多少？参考答案一、单选题（共有2道小题）1.A2.D二、填空题（共有6道小题）3.254.5.156.7.8.三、解答题（共有2道小题）9.解：（1）抛物线顶点坐标为（1,4）设由于抛物线过点B(0，3)解得解析式为，即（2）作点B关于x轴的对称点E（0，-3），连接AE交x轴于点P.设AE解析式，则解得当y=0时， 点P坐标为10.解，如图，将圆锥沿SA剪开并展开其侧面，则题目中要求的最短路径即为BB可求得在扇形SBB中，若假设BSB=n则，可求得BSB=n=60又SB=SB，BSB是等边三角形最短路径BB=12