八年级下册数学同步课程第11讲-分式方程与简单应用（提高）-教案

《八年级下册数学同步课程第11讲-分式方程与简单应用（提高）-教案》由会员分享，可在线阅读，更多相关《八年级下册数学同步课程第11讲-分式方程与简单应用（提高）-教案（13页珍藏版）》请在七七文库上搜索。

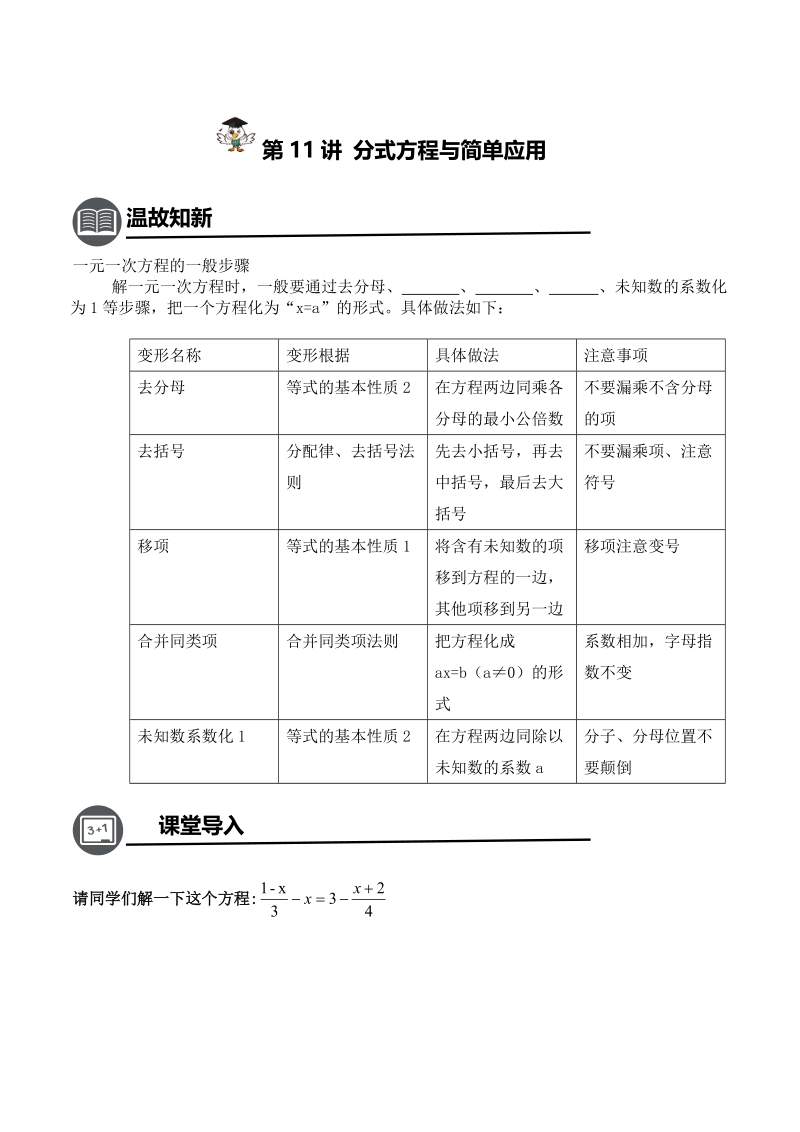
1、 2017年 2017年春季初二年级数学教材 A版第11讲 分式方程与简单应用 温故知新一元一次方程的一般步骤 解一元一次方程时，一般要通过去分母、 、 、 、未知数的系数化为1等步骤，把一个方程化为“x=a”的形式。具体做法如下： 变形名称变形根据具体做法注意事项去分母等式的基本性质2在方程两边同乘各分母的最小公倍数不要漏乘不含分母的项去括号分配律、去括号法则先去小括号，再去中括号，最后去大括号不要漏乘项、注意符号移项等式的基本性质1将含有未知数的项移到方程的一边，其他项移到另一边移项注意变号合并同类项合并同类项法则把方程化成ax=b（a0）的形式系数相加，字母指数不变未知数系数化1等式的基

2、本性质2在方程两边同除以未知数的系数a分子、分母位置不要颠倒课堂导入 请同学们解一下这个方程: 知识要点一一分式方程1.定义：分母中含有未知数的方程叫分式方程。2.注意未知数和字母的区别：未知数是字母，但字母不一定是未知数。例如，解关于的方程，这里的是未知数，但字母不是未知数，它是系数，故该方程不是分式方程。二解分式方程的步骤：（1）去分母，即在方程两边同时乘以最简公分母，把原方程化为整式方程；（2）解这个整式方程；（3）验根：把整式方程的根代入最简公分母中，使最简公分母不等于的根是原方程的根，否则，便是增根，必须舍去。 典例分析例1.判断下列关于、的方程中，是分式方程的有 。（填正确的序号）

3、 ；（、为常数）【解析】例2.下列关于的方程中，其中是分式方程的有 。 ；。【解析】【例3】解下列关于方程（1）； （2）。 【解析】,(增根）学霸说 举一反三1.给出下列关于方程中，是分式方程的有 。 ； 。【解析】2.在下列关于方程中，是分式方程的是（ ） A. B. C. D. 【解析】B3.解下列关于的方程（1） （2）【解析】，（3） （4） 【解析】(增根），(增根） 知识要点二一增根和无解问题1. 把整式方程的根代入最简公分母中，使最简公分母等于的根是原方程的增根。2. 方程无解问题：一是方程解出来，不存在，二是解出来的是增根二分式方程的解在某个范围时，求参数的范围 典例分析例1

4、当为何值时,解方程会产生增根?【解析】例2.为何值时，方程无解。【解析】例3.若关于的方程的解不大于13，求的取值范围。【解析】 举一反三1当为何值时,关于的方程会产生增根？【解析】2.若关于的分式方程无解，求常数的值【解析】3.若关于的方程的解不小于,求的取值范围。【解析】课堂闯关 初出茅庐 l 建议用时：10分钟1.下列各方程是关于的分式方程的是（ ） A. B. C. D. 【解析】C2. 如果方程的解是，则 。【解析】3. 方程的解是 。【解析】4.满足方程的值是( )A、1 B、 C、 D、没有【解析】C5.关于的方程，下列说法中不正确的是（ ） A、最简公分母是 B、方程两边同乘以

5、得整式方程C、解该分式方程对应的整式方程得 D、原方程的解为【解析】D6.若方程有增根，求的值。【解析】 优学学霸 l 建议用时：15分钟1 若方程无解,则m=_。 【解析】12. 如果关于x的方程无解，则的值为（ ）A、B、 C、 D、3【解析】B3. 解答题：（1） 若 是正整数，关于 的分式方程 的解为非负数，求 的值；（2）若关于 的分式方程 总无解，求 的值【解析】（1） 由 得 ，化简得 ，因为 为非负数，所以 ，即 又 是正整数，所以 且当 时 时原方程是非负解（2） 去分母，得即若 ，显然方程无解；若 ，当 时， 不存在；当 时，综上： 的值 ，考场直播 1（2016黑龙江四模

6、）若分式方程=有增根，则增根为（）Ax=1 Bx=1 Cx=1Dx=0【解答】解：原方程有增根，最简公分母x1=0，解得x=1故选：B2（2016梅州）对于实数a、b，定义一种新运算“”为：ab=，这里等式右边是实数运算例如：13=则方程x（2）=1的解是（）Ax=4 Bx=5 Cx=6 Dx=7【解答】解：根据题意，得=1，去分母得：1=2（x4），解得：x=5，经检验x=5是分式方程的解故选B自我挑战l 建议用时：30分钟 1下列关于x的方程中，是分式方程的是（）A3x= B=2 C= D3x2y=1【解答】解：A、C、D项中的方程分母中不含未知数，故不是分式方程；B、方程分母中含未知数x

7、，故是分式方程，故选B2若关于x的方程有增根，则m的值为（）A0 B1 C1 D2【解答】选C3在下列方程x2x+；3=a+4；+5x=6；+=1中，是分式方程的有（）A1个 B2个 C3个 D4个【解答】选：B4下列方程中，不是分式方程的是（）A BC D【解答】解：A、该方程符合分式方程的定义，属于分式方程，故本选项错误；B、该方程属于无理方程，故本选项正确；C、该方程符合分式方程的定义，属于分式方程，故本选项错误；D、该方程符合分式方程的定义，属于分式方程，故本选项错误；故选：B5（2016邵阳）分式方程=的解是（）Ax=1 Bx=1 Cx=2 Dx=3【解答】选：D6（2016潍坊）若

8、关于x的方程+=3的解为正数，则m的取值范围是（）Am Bm且m Cm Dm且m【解答】选：B7（2016柳州）分式方程的解为（）Ax=2 Bx=2 Cx= Dx=【解答】选B8（2016重庆）从3，1，1，3这五个数中，随机抽取一个数，记为a，若数a使关于x的不等式组无解，且使关于x的分式方程=1有整数解，那么这5个数中所有满足条件的a的值之和是（）A3 B2 C D【解答】解：解得，不等式组无解，a1，解方程=1得x=，x=为整数，a1，a=3或1或1，a=1时，原分式方程无解，故将a=1舍去，所有满足条件的a的值之和是2，故选B9（2016十堰）用换元法解方程=3时，设=y，则原方程可化

9、为（）Ay3=0 By3=0 Cy+3=0 Dy+3=0【解答】选：B10（2016雅安校级自主招生）已知x2=2+x，则代数式2x2+2x的值是（）A2 B6 C2或6 D2或6【解答】解：设x2+x=a，则原方程可化为a2=0，去分母得，a22a+3=0，解得a=1或a=3当a=1时，x2+x1=0，=1+4=50，此时x有解，原式=2（x2+x）=2a=2；当a=3时，x2+x+3=0，=112=110，此时x无解故选A11.（2016盐田区二模）关于x的方程有增根，那么a=（）A2 B0 C1 D3【解答】选D12.（2017莒县模拟）方程的解是（）Ax=1 Bx=1 Cx=2 Dx=

10、2【解答】选A13.在下列方程：、中，分式方程的个数有3【解答】解：分式方程有：，故答案为314下列方程：（1）=2；（2）=；（3）+=1（a，b为已知数）；（4）+=4其中是分式方程的是（1），（4）15.解分式方程：+=1【解答】解：方程两边同乘（x3），得：2x1=x3，整理解得：x=2，经检验：x=2是原方程的解16. 若解分式方程 时产生增根，则 的值为多少？【解析】去分母，得 增根为 ， 17. 关于 的方程 无解，则 的值为多少？2. ，【解答】去分母，得 .增根为 ， . 18. （2015春深圳校级期末）已知关于x的方程+1=无解，求a的值【解答】解：由原方程，得32x+x3=ax+12，整理，得（a+1）x=12当整式方程无解时，a+1=0即a=1，当分式方程无解时：x=3时，a=5，所以a=1或5时，原方程无解