 江苏省2020年2月高三最后一届特供模拟试卷数学试题含附加题(解析版)
江苏省2020年2月高三最后一届特供模拟试卷数学试题含附加题(解析版)
《江苏省2020年2月高三最后一届特供模拟试卷数学试题含附加题(解析版)》由会员分享,可在线阅读,更多相关《江苏省2020年2月高三最后一届特供模拟试卷数学试题含附加题(解析版)(16页珍藏版)》请在七七文库上搜索。
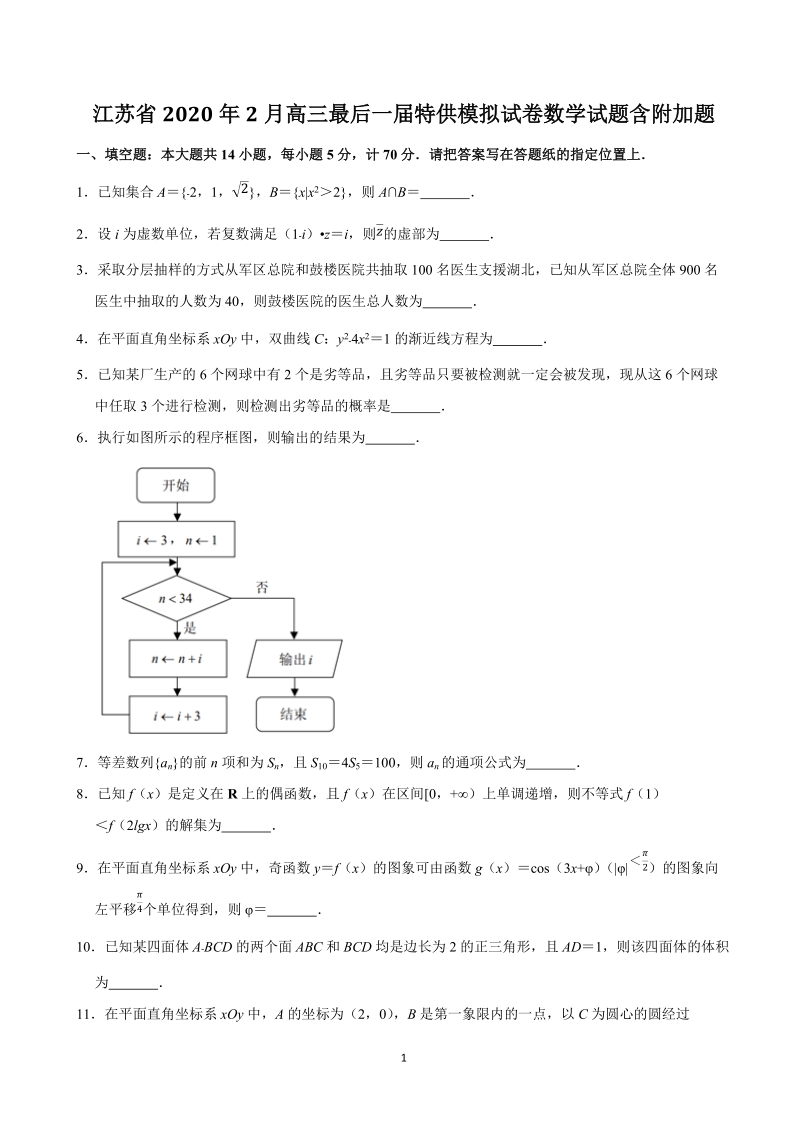
1、江苏省2020年2月高三最后一届特供模拟试卷数学试题含附加题一、填空题:本大题共14小题,每小题5分,计70分请把答案写在答题纸的指定位置上1已知集合A2,1,2,Bx|x22,则AB 2设i为虚数单位,若复数满足(1i)zi,则z的虚部为 3采取分层抽样的方式从军区总院和鼓楼医院共抽取100名医生支援湖北,已知从军区总院全体900名医生中抽取的人数为40,则鼓楼医院的医生总人数为 4在平面直角坐标系xOy中,双曲线C:y24x21的渐近线方程为 5已知某厂生产的6个网球中有2个是劣等品,且劣等品只要被检测就一定会被发现,现从这6个网球中任取3个进行检测,则检测出劣等品的概率是 6执行如图所示
2、的程序框图,则输出的结果为 7等差数列an的前n项和为Sn,且S104S5100,则an的通项公式为 8已知f(x)是定义在R上的偶函数,且f(x)在区间0,+)上单调递增,则不等式f(1)f(2lgx)的解集为 9在平面直角坐标系xOy中,奇函数yf(x)的图象可由函数g(x)cos(3x+)(|2)的图象向左平移4个单位得到,则 10已知某四面体ABCD的两个面ABC和BCD均是边长为2的正三角形,且AD1,则该四面体的体积为 11在平面直角坐标系xOy中,A的坐标为(2,0),B是第一象限内的一点,以C为圆心的圆经过O、A、B三点,且圆C在点A,B处的切线相交于P,若P的坐标为(4,2)
3、,则直线PB的方程为 12已知函数f(x)=x-1x,x0lnx+ex,x0,若g(x)f(x)kx有两个不等的零点,则实数k的取值范围为 13在ABC中,D为AC的中点,若cosDBC=35,cosDBA=725,且ABAC=2,则BABC的值为 14在平面直角坐标系xOy中,异于原点的A、B、C三点满足OA2+2OB2+3OC26,则ABC面积的最大值为 二、解答题:本大题共6小题,共计90分请在答题卡指定区域内作答,解答时应写出文字说明,证明过程或演算步骤15(14分)已知角(0,),且满足sin=154(1)若是锐角,求tan(-3);(2)若是钝角,求cos(2+4)16(14分)将
4、正方体ABCDA1B1C1D1沿三角形A1BC1所在平面削去一角可得到如图所示的几何体(1)连结BD,BD1,证明:平面BDD1平面A1BC1;(2)已知P,Q,R分别是正方形ABCD、CDD1C1、ADD1A1的中心(即对角线交点),证明:平面PQR平面A1BC117(14分)某工厂打算设计一种容积为2m3的密闭容器用于贮藏原料,容器的形状是如图所示的直四棱柱,其底面是边长为x米的正方形,假设该容器的底面及侧壁的厚度均可忽略不计(1)请你确定x的值,使得该容器的外表面积最小;(2)若该容器全部由某种每平方米价格为100元的材料做成,且制作该容器仅需将购置的材料做成符合需要的矩形,这些矩形即是
5、直四棱柱形容器的上下底面和侧面(假设这一过程中产生的费用和材料损耗可忽略不计),再将这些上下底面和侧面的边缘进行焊接即可做成该容器,焊接费用是每米500元,试确定x的值,使得生产每个该种容器的成本(即原料购置成本+焊接费用)最低18(16分)已知椭圆x2a2+y2b2=1(ab0)的左右焦点分别为F1、F2,左右顶点分别为A、B,上顶点为T,且TF1F2为等边三角形(1)求此椭圆的离心率e;(2)若直线ykx+m(k0)与椭圆交与C、D两点(点D在x轴上方),且与线段F1F2及椭圆短轴分别交于点M、N(其中M、N不重合),且|CM|DN|求k的值;设AD、BC的斜率分别为k1,k2,求k1k2
6、的取值范围19(16分)已知函数f(x)axax,a0且a1,函数g(x)=x1+x2(1)判断并证明f(x)和g(x)的奇偶性;(2)求g(x)的值域;(3)若xR,都有|f(x)|g(x)|成立,求a的取值范围20(16分)若数列an满足:对任意nN*,均有anbn+cn成立,且bn,cn都是等比数列,则称(bn,cn)是数列an的一个等比拆分(1)若an2n,且(bn,bn+1)是数列an的一个等比拆分,求bn的通项公式;(2)设(bn,cn)是数列an的一个等比拆分,且记bn,cn的公比分别为q1,q2;若an是公比为q的等比数列,求证:q1q2q;若a11,a22,q1q21,且对任
7、意nN*,an+13anan+1an+2+an+2an恒成立,求a3的取值范围选做题(在21、22、23三小题中选做2题,若多做按前两题计分,每小题10分,计20分请把答案写在答题纸的指定区域内)选修4-2:矩阵与变换21(10分)已知A=31-10,=32,求A1a选修4-4:坐标系与参数方程22(10分)曲线C的参数方程为x=1-2t21+2t2y=22t1+2t2,直线l的参数方程为x=1+2ay=3a(1)求曲线C的一般方程;(2)求直线l被曲线C截得的弦长选修4-5:不等式选讲23已知x,y0,且xy4,证明:yx2+4+xy2+412必做题(第24、25题,每小题10分,计20分请
8、把答案写在答题纸的指定区域内)24(10分)如图所示是一个上下底面均是边长为2的正三角形的直三棱柱,且该直三棱柱的高为4,D为AB的中点,E为CC1的中点(1)求DE与平面ABC夹角的正弦值;(2)求二面角AA1DE的余弦值25(10分)在平面直角坐标系xOy中,已知点A1,A2,An,B1,B2,Bn,均在抛物线xy2上,线段AnBn与x轴的交点为Hn将OA1B1,H1A2B2,HnAn+1Bn+1,的面积分别记为S1,S2,Sn+1,已知上述三角形均为等腰直角三角形,且它们的顶角分别为O,H1,Hn,(1)求S1和S2的值;(2)证明:nsnn2一、填空题:本大题共14小题,每小题5分,计
9、70分请把答案写在答题纸的指定位置上1【详解详析】集合A2,1,2,Bx|x22x|x-2或x2,AB2故答案为:22【详解详析】由(1i)zi,得z=i1-i=i(1+i)(1-i)(1+i)=-12+12i,z=-12-12i,则z的虚部为-12故答案为:-123【详解详析】已知从军区总院全体900名医生中抽取的人数为40,则则从鼓楼医院抽取的医生总人数为1004060,设鼓楼医院的医生总人数为m,这由60m=40900,m1350,故答案为:13504【详解详析】由题意a21,b2=14,焦点在y轴上,所以渐近线的方程为:y=abx,即y2x,故答案为:y2x5【详解详析】某厂生产的6个
10、网球中有2个是劣等品,且劣等品只要被检测就一定会被发现,现从这6个网球中任取3个进行检测,基本事件总数n=C63=20,检测出劣等品包含的基本事件个数m=C21C42+C22C41=12,则检测出劣等品的概率是p=mn=1220=35故答案为:356【详解详析】i3,n1,第一次执行循环体后,n4,i6,不满足退出循环的条件;第二次执行循环体后,n10,i9,不满足退出循环的条件;第三次执行循环体后,n19,i12,不满足退出循环的条件;第四次执行循环体后,n31,i15,不满足退出循环的条件;第五次执行循环体后,n46,i18,满足退出循环的条件;故答案为:输出i值为18,7【详解详析】设公
11、差为d,由S104S5100,可得10a1+1092d=1005a1+542d=25,解得a11,d2,故an2n1,故答案为:an2n18【详解详析】函数f(x)是偶函数,xR,都有f(x)f(x)f(|x|);又由于f(x)在区间0,+)上单调递增,不等式f(1)f(2lgx)f(1)f(|2lgx|)12|lgx|;lgx12或lgx-12解得x10或0x1010;不等式f(1)f(2lgx)的解集为:x|x10或0x1010故答案为:x|x10或0x10109【详解详析】由题意可得函数g(x)cos(3x+)(|2)的图象向左平移4个单位得到奇函数yf(x)的图象,而把函数g(x)co
12、s(3x+)(|2)的图象向左平移4个单位得到ycos(3x+34+)的图象,34+k+2,kZ,=-4,故答案为:-410【详解详析】如图,ABC与BCD均为等边三角形,边长为2,AD1,取AD中点O,连接OB,OC,可得OBOC=22-(12)2=152,SOBC=122(152)2-12=112VA-BCD=131121=116故答案为:11611【详解详析】根据题意,A的坐标为(2,0),以C为圆心的圆经过O、A、B三点,则圆心C在线段OA的垂直平分线上,设圆心C的坐标为(1,b),圆C在点A,B处的切线相交于P,若P的坐标为(4,2),则kPA=2-04-2=1,则kAC=b-01-
13、2=-1,解可得:b1,即C(1,1),圆C的半径r|AC|=2,其圆C的方程为(x1)2+(y1)22,直线PB的斜率必定存在,设PB的方程为y2k(x4),即kxy4k+20,则有|-3k+1|1+k2=2,解可得k=-17或1(舍);故PB的方程为y2=-17(x4),变形可得x+7y180;故答案为:x+7y18012【详解详析】函数g(x)f(x)kx有两个不等的零点,即方程f(x)kx有2个不等根,因为x0,所以也等价于f(x)x=k有2个不等实根,根据条件令h(x)=f(x)x=1-1x2,x0lnxx+e,x0,因为x0时,h(x)1-1x21,x0时,h(x)=1-lnxx2
14、,当0xe时,h(x)单调递增,当xe时,h(x)单调递减,且当x+时,h(x)e,作出函数f(x)的图象如图:根据图象可知,k(,1)(e,e+1e),故答案为:(,1)(e,e+1e)13【详解详析】记ABc,ACb,BCa,则ABAC=cbcosBAC=b2+c2-a22=2,即b24+a2c2,因为D为AC的中点,所以SDCBSDBA,即45a=2425c,所以a=65c,又由cosABCcos(DBA+DBA)=72535-242545=-35=a2+c2-b22ac,解得c2=5043,则BABC=-35ac=-3565c2=-3643,故答案为:-364314【详解详析】如图,以


- 配套讲稿:
如PPT文件的首页显示word图标,表示该PPT已包含配套word讲稿。双击word图标可打开word文档。
- 特殊限制:
部分文档作品中含有的国旗、国徽等图片,仅作为作品整体效果示例展示,禁止商用。设计者仅对作品中独创性部分享有著作权。
- 关 键 词:
- 江苏省 2020 月高三 最后 特供 模拟 试卷 数学试题 附加 解析
 七七文库所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
七七文库所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。



 浙公网安备33030202001339号
浙公网安备33030202001339号
链接地址:https://www.77wenku.com/p-127262.html