著名机构高二数学理科秋季班讲义第4讲 距离问题与动点问题 删解析

《著名机构高二数学理科秋季班讲义第4讲 距离问题与动点问题 删解析》由会员分享，可在线阅读，更多相关《著名机构高二数学理科秋季班讲义第4讲 距离问题与动点问题 删解析（13页珍藏版）》请在七七文库上搜索。

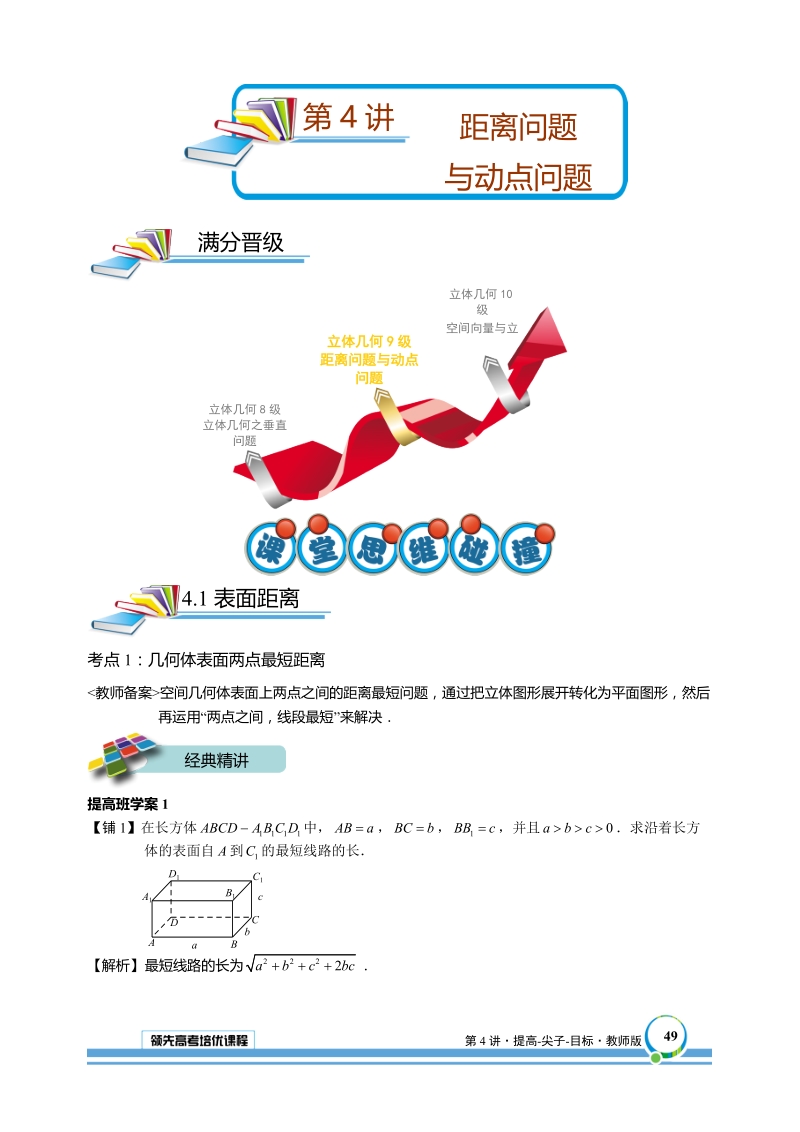
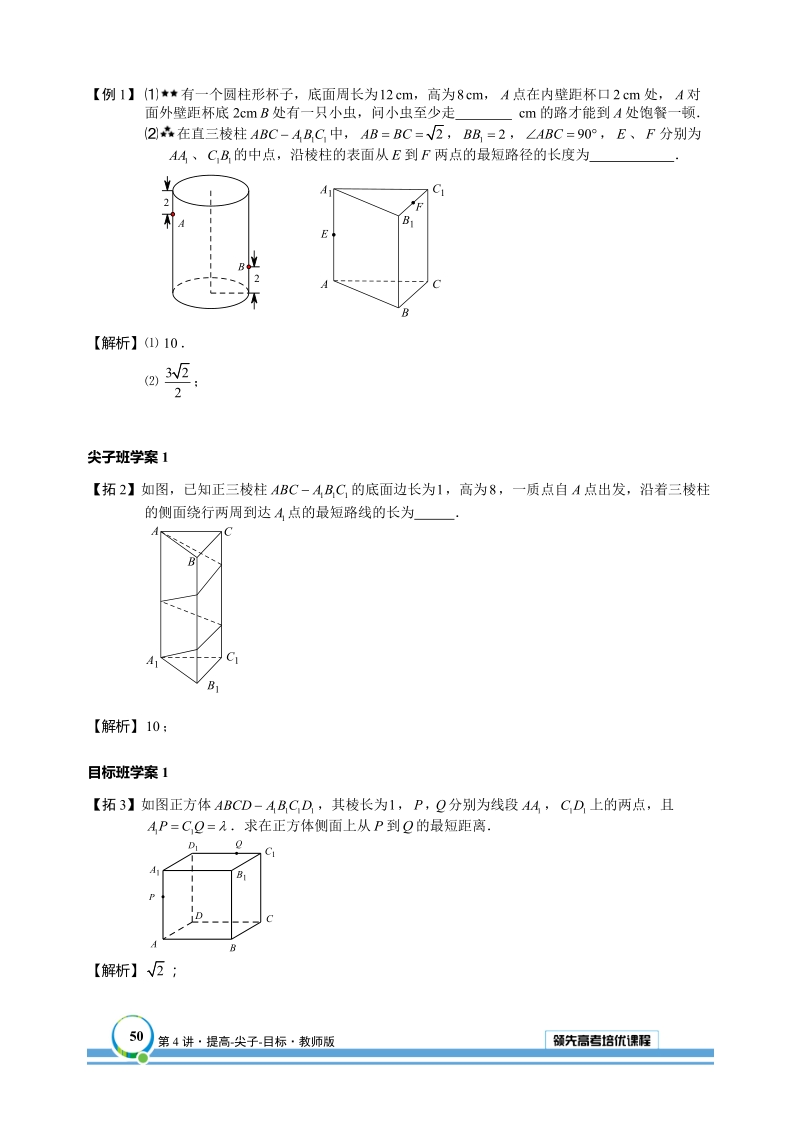
1、距离问题与动点问题第4讲 满分晋级 立体几何10级空间向量与立体几何综合立体几何8级立体几何之垂直问题立体几何9级距离问题与动点问题4.1表面距离考点1：几何体表面两点最短距离空间几何体表面上两点之间的距离最短问题，通过把立体图形展开转化为平面图形，然后再运用“两点之间，线段最短”来解决经典精讲提高班学案1【铺1】在长方体中，并且求沿着长方体的表面自到的最短线路的长【解析】 最短线路的长为【例1】 有一个圆柱形杯子，底面周长为cm，高为cm，点在内壁距杯口cm处，对面外壁距杯底2cm处有一只小虫，问小虫至少走 cm的路才能到处饱餐一顿在直三棱柱中，、分别为、的中点，沿棱柱的表面从到两点的最短路

2、径的长度为 【解析】 ；尖子班学案1【拓2】如图，已知正三棱柱的底面边长为，高为，一质点自点出发，沿着三棱柱的侧面绕行两周到达点的最短路线的长为 【解析】 ；目标班学案1【拓3】如图正方体，其棱长为，分别为线段，上的两点，且求在正方体侧面上从到的最短距离【解析】 ；【备选】已知以为顶点的正四面体，其棱长为，分别为上的两点，且（）求在正四面体表面上从到的最短距离【解析】 4.2等积法与点面距离考点2：多面体的体积知识点睛对于规则的几何体，如棱柱、棱锥等，直接套用公式即可体积的求解与计算是立体几何学习的重点，其方法灵活多变比较常见的求体积的方法有三种：分割法：把不规则的几何体分割成规则的几何体；当

3、规则几何体的体积用公式不易求出时，再将其分割，转化成比较好求体积的几何体补形法：把不规则形体补成规则形体，不熟悉的几何体补成熟悉的几何体，便于计算常见的补形有：将正四面体补成正方体；将等腰四面体（对棱相等）补成长方体；将三条棱两两相互垂直且相等的三棱锥补成正方体；将台体补成椎体等等等积法：选择合适的底面来求多面体的体积分割和补形是求几何体体积的常用方法，要注意理清分割或补形前后几何体体积之间的数量关系补形法不但对求体积比较方便，对解决别的立体几何问题往往也很有用经典精讲【例2】 在三棱锥中，、都是等边三角形，平面平面，则三棱锥的体积为_三棱锥的三条侧棱两两垂直，为中点，为中点，则三棱锥的体积为

4、_；四棱锥的体积为_（2010年复旦自主招生）设一个多面体从前面、后面、左面、右面、上面看到的图形为：则该多面体的体积为（ ）A B C D【解析】 ； ； D尖子班学案2【拓2】设三棱柱的体积为，、分别是侧棱、上的点，且，则四棱锥的体积为_【解析】 ；【备选】在如图所示的三棱柱中，点、的中点以及的中点所决定的平面把三棱柱切割成体积不相同的两部分，问小部分的体积和大部分的体积比为（ ）A B C D【解析】 D考点3：点面距离知识点睛1点在直线上的射影 自点向直线引垂线，垂足叫做点在直线上的射影点到垂足的距离叫点到直线的距离2点在平面内的射影 自点向平面引垂线，垂足叫做点在平面内的射影，这点和

5、垂足间的线段叫做这点到平面的垂线段垂线段的长度叫做这点到这个平面的距离3斜线在平面内的射影一条直线和一个平面相交，但不和这个平面垂直，这条直线叫做这个平面的斜线，斜线和平面的交点叫做斜足，斜线上一点和斜足间的线段，叫做这点到平面的斜线段过斜线上斜足以外的一点向平面引垂线，过垂足和斜足的直线叫做斜线在这个平面内的射影，垂足与斜足间的线段叫做这点到平面的斜线段在这个平面内的射影4求点面距离的方法：直接法：直接作面的垂线，确定垂足的位置；等体积法：对同一个三棱锥，从不同的角度选择底和高计算体积并加以比较即可转化法：转化成求另一点到该平面的距离，常见的是转化为求与面平行的直线上的点到面的距离如果可以直

6、接作出点到平面的垂线，确定垂足位置的话，可以直接解直角三角形得出比如求正三棱锥顶点到地面的距离，可以过顶点作底面的垂线，垂足是底面的中心，然后计算即可求得距离又比如两个平面垂直，要求其中一个面上的点到另一个面的距离，只需过此点作两个面的交线的垂线，点与垂足间的距离即为所求如果直接作垂线段不易求解，但是底面积和体积容易求解的话，用等积法比较好与平面平行的直线（或平面）上的点到该平面的距离相等，利用这一点，可以将要求的点面距离转化为其它的较易求解的点面距离还有一种较常见的是将要求的点面距离与另一个点面距离建立比例关系，间接求出例3是直接法，例4是等积法（也可以用直接法），例5是转化法经典精讲【例3

7、】 如图，梯形中，面，求点到平面的距离 【解析】 提高班学案2【铺1】如图，正方体的边长为，则到平面的距离为 【解析】 ；【例4】 已知长方体中，棱，棱求点到平面的距离求点到平面的距离【解析】 ； ；尖子班学案3【拓2】（2011年卓越联盟）在直三棱柱中，底面边长与侧棱长均等于，且为的中点，则点到平面的距离为（ ）A B C D【解析】 D目标班学案2【拓3】已知为棱长为的正方体的棱的中点，求点到平面的距离【解析】 ；提高班学案3【铺1】设是正三棱柱，底面边长和高都是，是侧面的中心点，则到侧面的对角线的距离是（ ）A B C D【解析】 C【例5】 在棱长为的正方体中，、分别为棱、的中点，为棱

8、上的一点，且，则点到平面的距离为（ ）ABCD正六棱锥中，为的中点，则三棱锥与三棱锥体积之比为（ ）A B C D【解析】 D； C；目标班学案3【拓3】在棱长为的正方体中，为的中点 求证：四面体与四面体的体积相等； 求点到平面的距离【解析】 连结，则，又平面，平面，平面，点与点到平面的距离相等四面体与四面体的体积相等； 4.3动点问题探索考点4：动点轨迹问题知识点睛在立体几何问题中，当一个点在一定的约束条件下位置可以变动时，称这类问题为“动点问题”动点问题是综合性很强的问题，一般的思路是将问题特殊化、空间问题平面化，多需要进行分类讨论动点问题不是研究固定的点、线、面之间的位置关系，而是在运动

9、中找出其中的变化规律，对知识的灵活应用及迁移能力要求较高这类问题只能在重视基础知识的前提下，进行适当的练习、体会和总结，才能找到解决这类问题的思路用一个词来概括解决方法的话，就是“转化”经典精讲【例6】 正方体中，是正方形内的动点，则点的轨迹是（ ）A点B线段C线段D平面正方体中，点在四边形及其边界上运动，并且总保持，则动点的轨迹是（）A线段 B线段C的中点与的中点的连线 D的中点与的中点的连线 【解析】 B； A；考点5：动点体积问题动点体积问题主要要考虑的就是底面积和高在动点变化中的变化情况，选择合适的底面就显得比较重要动点体积问题在高考中属于难题，有时候可以通过特殊位置或特殊点来解决问题

10、经典精讲【例7】 如图，正方体的棱长为1，线段上有两个动点，且，则下列结论中错误的是（ ）A B平面 C三棱锥的体积为定值D的面积与的面积相等【追问】三棱锥的体积是定值吗？（2010年海淀二模7）在正四面体中，棱长为4，是BC的中点，在线段上运动（不与、重合），过点作直线平面，与平面交于点，给出下列命题：面；点一定在直线上；其中正确的是（ ）A B C D（2010北京理8）如图，正方体的棱长为2，动点，在棱上，动点，分别在棱，上，若，（大于零），则四面体的体积（）A与都有关 B与有关，与无关C与有关，与无关 D与有关，与无关 【解析】 D【追问】三棱锥的体积是定值 A D【备选】已知直四棱柱

11、的各棱长均为，长为的线段的一个端点在上运动，另一个端点在底面上运动，则的中点的轨迹（曲面）与共一顶点的三个面围成的几何体的体积为_【解析】 ；中，是的中点，将沿翻折，使得两点间的距离为，则三棱锥的体积等于（ ）ABCD原图：解析图：【解析】 D；由已知有，又，由，过作面的垂线，设垂足为，则又，面，同理，于是，实战演练【演练1】一个圆柱形茶杯的主视图为边长为的正方形，直观图如下，它左边下方有一只蚂蚁，从处沿杯子侧面爬行到对面的中点处，如果蚂蚁爬行路线最短，则路线长为_原图： 【解析】 ；【演练2】若正四棱柱的底面边长为，则点到底面的距离为（ ）ABCD【解析】 D【演练3】在三棱锥中，已知，且，

12、则三棱锥的体积为_【解析】 ；【演练4】如图，已知为外一点，平面，垂足为，若、两两垂直，且，求点到平面的距离【解析】【演练5】如图，、是空间四点，在中，等边所在的平面以为轴可转动当转动过程中，是否总有？请证明你的结论【解析】 当在转动过程中，总有，平面，当转动到与共面时，仍然有故转动过程中，总有【演练6】如图，在长方体中，分别过，的两个平行截面将长方体分成三部分，其体积分别记为，若，则截面的面积为 【解析】大千世界在棱长为的正方体中，、分别为、的中点求四面体的体积原图： 解析图：【解析】 法一：连结，则点是线段的中点，于是；，故法二：取的中点，连结，平面于是，故61第4讲提高-尖子-目标教师版