决胜2019中考数学之模型解题高分攻略专题03相似三角形模型解题（教师版）

《决胜2019中考数学之模型解题高分攻略专题03相似三角形模型解题（教师版）》由会员分享，可在线阅读，更多相关《决胜2019中考数学之模型解题高分攻略专题03相似三角形模型解题（教师版）（19页珍藏版）》请在七七文库上搜索。

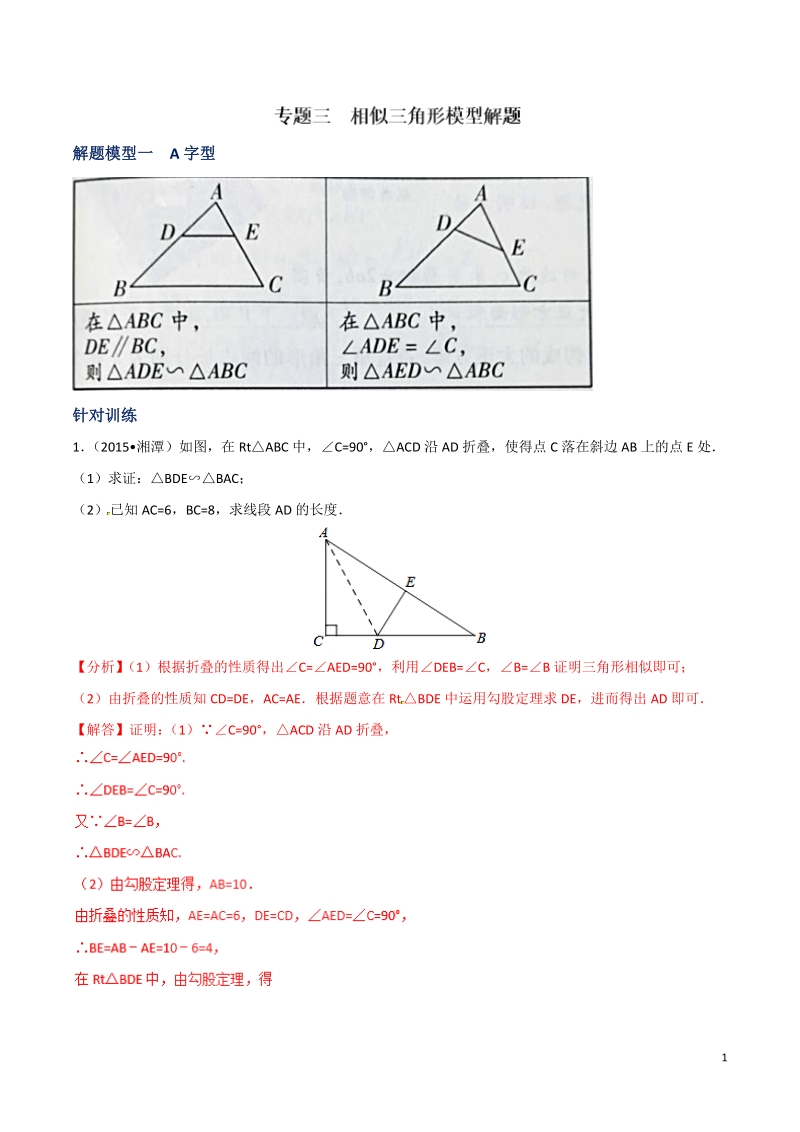
1、 1 解题模型一解题模型一 A 字型字型 针对训练针对训练 1 （2015湘潭）如图，在 RtABC 中，C=90，ACD 沿 AD 折叠，使得点 C 落在斜边 AB 上的点 E 处 （1）求证：BDEBAC； （2）已知 AC=6，BC=8，求线段 AD 的长度 【分析】 （1）根据折叠的性质得出C=AED=90，利用DEB=C，B=B 证明三角形相似即可； （2）由折叠的性质知 CD=DE，AC=AE根据题意在 RtBDE 中运用勾股定理求 DE，进而得出 AD 即可 【解答】证明： （1）C=90，ACD 沿 AD 折叠， 2 【点睛】本题考查了相似三角形的判定和性质，关键是根据 1、折

2、叠的性质：折叠是一种对称变换，它属于 轴对称，根据轴对称的性质，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等；2、勾 股定理求解 2 （2018黄石）在ABC 中，E、F 分别为线段 AB、AC 上的点（不与 A、B、C 重合） （1）如图 1，若 EFBC，求证： （2）如图 2，若 EF 不与 BC 平行， （1）中的结论是否仍然成立？请说明理由； （3）如图 3，若 EF 上一点 G 恰为ABC 的重心，求的值 【分析】 （1）由 EFBC 知AEFABC，据此得=，根据=（）2即可得证； （2） 分别过点 F、 C 作 AB 的垂线， 垂足分别为 N、 H， 据此知AFN

3、ACH， 得=， 根据= 即可得证； （3） 连接AG并延长交BC于点M， 连接BG并延长交AC于点N， 连接MN， 由重心性质知SABM=SACM、=， 设=a，利用（2）中结论知=、=a，从而得 3 =+a， 结合=a 可关于 a 的方程， 解之求得 a 的值即可得出 答案 =. =. （3）如图 2，连接 AG 并延长交 BC 于点 M，连接 BG 并延长交 AC 于点 N，连接 MN，则 MN 分别是 BC、 AC 的中点， 4 【点睛】本题主要考查相似形的综合问题，解题的关键是熟练掌握相似三角形的判定与性质和三角形重心 的定义及其性质等知识点 # 3 （2017衢州）如图，AB 为半

4、圆 O 的直径，C 为 BA 延长线上一点，CD 切半圆 O 于点 D，连接 OD作 BE CD 于点 E，交半圆 O 于点 F已知 CE=12，BE=9 （1）求证：CODCBE； （2）求半圆 O 的半径 r 的长 5 【分析】 （1）由切线的性质和垂直的定义得出E=90=CDO，再由C=C，得出CODCBE （2）由勾股定理求出 BC=15，由相似三角形的性质得出比例式，即可得出答案 【点睛】本题考查了切线的性质、相似三角形的判定及其性质、勾股定理；熟练掌握相似三角形的判定与 性质是解决问题的关键 4 （2017杭州）如图，在锐角三角形 ABC 中，点 D，E 分别在边 AC，AB 上，

5、AGBC 于点 G，AFDE 于点 F，EAF=GAC （1）求证：ADEABC； （2）若 AD=3，AB=5，求的值 6 【分析】 （1）由于 AGBC，AFDE，所以AFE=AGC=90，从而可证明AED=ACB，进而可证明ADE ABC； （2）ADEABC，又易证EAFCAG，所以，从而可知 来源:Z&xx&k.Com 【点睛】本题考查相似三角形的判定，解题的关键是熟练运用相似三角形的判定，本题属于中等题型来源:Z&X&X&K 7 解题模型二解题模型二 8 字型字型 针对训练针对训练 5 （2018江西）如图，在ABC 中，AB=8，BC=4，CA=6，CDAB，BD 是ABC 的平

6、分线，BD 交 AC 于点 E，求 AE 的长 【分析】根据角平分线定义和平行线的性质求出D=CBD，求出 BC=CD=4，证AEBCED，得出比例 式，求出 AE=2CE，即可得出答案 =. =. 8 AE=2CE. AC=6=AE+CE， AE=4 【点睛】 本题考查了相似三角形的性质和判定和等腰三角形的判定、 平行线的性质等知识点， 能求出 AE=2CE 和ABECDE 是解此题的关键 6 （2017来宾）如图，在正方形 ABCD 中，H 为 CD 的中点，延长 AH 至 F，使 AH=3FH，过 F 作 FGCD， 垂足为 G，过 F 作 BC 的垂线交 BC 的延长线于点 E （1）

7、求证：ADHFGH； （2）求证：四边形 CEFG 是正方形 【分析】 （1）由正方形的性质以及 FGCD 得出ADH=FGH=90，结合对顶角AHD=FHG，即可判定 ADHFGH； # （2） 根据三角形相似的性质得出 GF=CG， 再根据已知条件 FGCD， DCBE， FEBE， 即可判定四边形 CEFG 是正方形 =3. GF=AD，DH=CH， CG=2GH. 9 CD=6GH. CG=CD. GF=CG. FGCD，DCBE，FEBE， 四边形 CEFG 是正方形 【点睛】本题考查了相似三角形的判定和性质，正方形的判定和性质，熟练掌握性质定理是解题的关键 解题模型三解题模型三 母

8、子型母子型 针对训练针对训练 7 （2018东营）如图，CD 是O 的切线，点 C 在直径 AB 的延长线上 （1）求证：CAD=BDC； （2）若 BD=AD，AC=3，求 CD 的长 求出 CD 的长 【解答】 （1）证明：连接 OD，如图所示来源: 10 CD=2 【点睛】本题考查了相似三角形的判定与性质、圆周角定义以及切线的性质，解题的关键是： （1）利用等 角的余角相等证出CAD=BDC； （2）利用相似三角形的性质找出 # 解题模型四解题模型四 一线三等角型一线三等角型 11 针对训练针对训练 8 （2018杭州）如图，在ABC 中，AB=AC，AD 为 BC 边上的中线，DEAB

9、 于点 E （1）求证：BDECAD （2）若 AB=13，BC=10，求线段 DE 的长 【分析】 （1）想办法证明B=C，DEB=ADC=90即可解决问题； （2）利用面积法：ADBD=ABDE 求解即可； 【点睛】本题考查相似三角形的判定和性质、等腰三角形的性质等知识，解题的关键是熟练掌握基本知识， 12 学会利用面积法确定线段的长 9 （2018盐城节选）如图，已知等边ABC，将直角三角板的 60角顶点 D 任意放在 BC 边上（点 D 不与点 B、C 重合） ，使两边分别交线段 AB、AC 于点 E、F （1）若 AB=6，AE=4，BD=2，则 CF= ； （2）求证：EBDDCF

10、 【分析】 （1）先求出 BE 的长度后发现 BE=BD 的，又B=60，可知BDE 是等边三角形，可得BDE=60， 另外DEF=60，可证得CDF 是等边三角形，从而 CF=CD=BCBD； % （2）证明EBDDCF，这个模型可称为“一线三等角相似模型”，根据“AA”判定相似. CDF+BDE=120，BED+BDE=120. BED=CDF 13 又B=C=60， EBDDCF. 10 （2017东营）如图，在等腰三角形 ABC 中，BAC=120，AB=AC=2，点 D 是 BC 边上的一个动点（不与 B、C 重合） ，在 AC 上取一点 E，使ADE=3 0 （1）求证：ABDDC

11、E； （2）设 BD=x，AE=y，求 y 关于 x 的函数关系式并写出自变量 x 的取值范围； （3）当ADE 是等腰三角形时，求 AE 的长 【解答】证明： （1）ABC 是等腰三角形，且BAC=120， ABD=ACB=30. ABD=ADE=30. ADC=ADE+EDC=ABD+DAB， EDC=DAB. ABDDCE. （2）如图 1，AB=AC=2，BAC=120， 14 （3）当 AD=DE 时，如图 2， 由（1）可知：此时ABDDCE， # 则 AB=CD，即 2=2x， x=22，代入 y=x+2， 解得 y=42，即 AE=42. 当 AE=ED 时，如图 3， EAD

12、=EDA=30，AED=120， DEC=60，EDC=90， 则 ED=EC，即 y=（2y）. 解得 y=，即 AE=. 当 AD=AE 时， AED=EDA=30，EAD=120， 此时点 D 与点 B 重合，不符合题意，此情况不存在， 15 当ADE 是等腰三角形时，AE=42或 【点睛】本题是相似形的综合题，考查了三角形相似的性质和判定、等腰三角形的性质、直角三角形 30角 的性质，本题的几个问题全部围绕ABDDCE，解决问题；难度适中 解题模型五解题模型五 一线三垂直型一线三垂直型 针对训练针对训练 11 （2018梧州）如图，AB 是M 的直径，BC 是M 的切线，切点为 B，C

13、 是 BC 上（除 B 点外）的任意 一点，连接 CM 交M 于点 G，过点 C 作 DCBC 交 BG 的延长线于点 D，连接 AG 并延长交 BC 于点 E （1）求证：ABEBCD； （2）若 MB=BE=1，求 CD 的长度 【分析】 （1）根据直径所对圆周角和切线性质，证明三角形相似； （2）利用勾股定理和面积法得到 AG、GE，根据三角形相似求得 GH，得到 MB、GH 和 CD 的数量关系，求 得 CD 【解答】 （1）证明：BC 为M 切线，来源:ZXXK ABC=90. DCBC， BCD=90. ABC=BCD. 16 AB 是M 的直径， AGB=90，即 BGAE. C

14、BD=A. ABEBCD. （2）解：过点 G 作 GHBC 于点 H. GH= . 又GHAB， & 17 【点睛】本题是几何综合题，综合考察了圆周角定理、切线性质和三角形相似解答时，注意根据条件构 造相似三角形 12 （2018武汉）在ABC 中，ABC=90 （1）如图 1，分别过 A、C 两点作经过点 B 的直线的垂线，垂足分别为 M、N，求证：ABMBCN； （2）如图 2，P 是边 BC 上一点，BAP=C，tanPAC=，求 tanC 的值； （3）如图 3，D 是边 CA 延长线上一点，AE=AB，DEB=90，sinBAC=，直接写出 tanCEB 的 值 【分析】 （1）利

15、用同角的余角相等判断出BAM=CBN，即可得出结论； （2） 先判断出 MP=MC， 进而得出=， 设 MN=2m， PN=m， 根据勾股定理得， PM=3m=CM， 即可得出结论； （3）先判断出=，再同（2）的方法，即可得出结论 【解答】解： （1）AMMN，CNMN， AMB=BNC=90. BAM+ABM=90. ABC=90， 18 （3）在 RtABC 中，sinBAC=， 如图 3，过点 A 作 AGBE 于 G，过点 C 作 CHBE 交 EB 的延长线于点 H. DEB=90， CHAGDE. % = . 同（1）的方法得，ABGBCH， .来源:ZXXK 设 BG=4m，CH=3m，AG=4n，BH=3n， AB=AE，AGBE， EG=BG=4m. 19 【点睛】此题是相似形综合题，主要考查了同角的余角相等，相似三角形的判定和性质，锐角三角函数， 平行线分线段成比例定理，构造图 1 是解本题的关键