2019-2020学年湖南省长沙市岳麓区麓山国际学校八年级（下）月考数学试卷（3月份）含详细解答

《2019-2020学年湖南省长沙市岳麓区麓山国际学校八年级（下）月考数学试卷（3月份）含详细解答》由会员分享，可在线阅读，更多相关《2019-2020学年湖南省长沙市岳麓区麓山国际学校八年级（下）月考数学试卷（3月份）含详细解答（21页珍藏版）》请在七七文库上搜索。

1、2019-2020 学年湖南省长沙市岳麓区麓山国际学校八年级（下）月考数学试卷（3 月份）一选择题（共 12 小题，满分小题，满分 36 分，每小题分，每小题 3 分）分） 1 （3 分）若一组数据 2，3，x，5，6，7 的众数为 7，则这组数据的中位数为（ ） A2 B3 C5.5 D7 2 （3 分）为调查某班学生每天使用零花钱的情况，童老师随机调查了 30 名同学，结果如 下表： 每天使用零花 钱（单位：元）  5 10 15 20 25 人数 2 5 8 x 6 则这 30 名同学每天使用的零花钱的众数和中位数分别是（ ） A15、15 B20、17.5 C20、20 D2

2、0、15 3 （3 分）在数据 1，3，5，7，9 中再添加一个数据，使得该组数据的平均数不变，则添加 的数据为（ ） A25 B3 C4.5 D5 4 （3 分）某射击运动员练习射击，5 次成绩分别是：8、9、7、8、x（单位：环） ，下列说 法中正确的个数是（ ） 若这 5 次成绩的平均数是 8，则 x8； 若这 5 次成绩的中位数为 8，则 x8； 若这 5 次成绩的众数为 8，则 x8： 若这 5 次成绩的方差为 8，则 x8 A1 个 B2 个 C3 个 D4 个 5 （3 分）已知1 是关于 x 的一元二次方程 ax2+bx+10 的一个根，则 ab 的值是 （ ）  A

3、1 B0 C1 D2 6 （3 分）利用配方法解一元二次方程 x26x+70 时，将方程配方为（xm）2n，则 m、 n 的值分别为（ ） Am9，n2 Bm3，n2 Cm3，n0 Dm3，n2 7 （3 分）方程 x（x5）x5 的根是（ ） Ax5 Bx0 Cx15，x20 Dx15，x21 第 2 页（共 21 页） 8 （3 分）图中信息是小明和小华射箭的成绩，两人都射了 10 箭，则射简成绩的方差较大 的是（ ） A小明 B小华 C两人一样 D无法确定 9 （3 分）有 5 人患了流感，经过两轮传染后共有 605 人患流感，则第一轮后患流感的人数 为（ ） A10 B50 C55 D

4、45 10 （3 分）如果（m+2）x|m|+mx10 是关于 x 的一元二次方程，那么 m 的值为（ ） A2 或2 B2 C2 D0 11 （3 分）若关于 x 的一元二次方程（k+2）x22x10 有实数根，则实数 k 的取值范围 是（ ） Ak3 Bk3 Ck3 且 k2 Dk3 且 k2 12 （3 分）设 a，b 是方程 x2+3x20170 的两个实数根，则 a2+2ab 的值为（ ） A2017 B2018 C2019 D2020 二填空题（共二填空题（共 6 小题，满分小题，满分 18 分，每小题分，每小题 3 分）分） 13 （3 分）数据3，6，0，5 的极差为 &nbs

5、p; 14 （3 分）某单位定期对员工按照专业能力、工作业绩、考勤情况三方面进行考核（每项 满分 100 分） ，三者权重之比为 3：5：2小明经过考核后三项务数分别为 90 分，86 分、 83 分，则小明的最后得分为   分 15 （3 分） 已知样本数据 x1， x2， x3， x4的方差为 2， 则 4x1， 4x2， 4x3， 4x4的方差是    16 （3 分）若关于 x 的一元二次方程（x+a）2b 有实数根，则 b 的取值范围是    17 （3 分）若 a，b 是一元二次方程 x22x+10 的两根，则   18

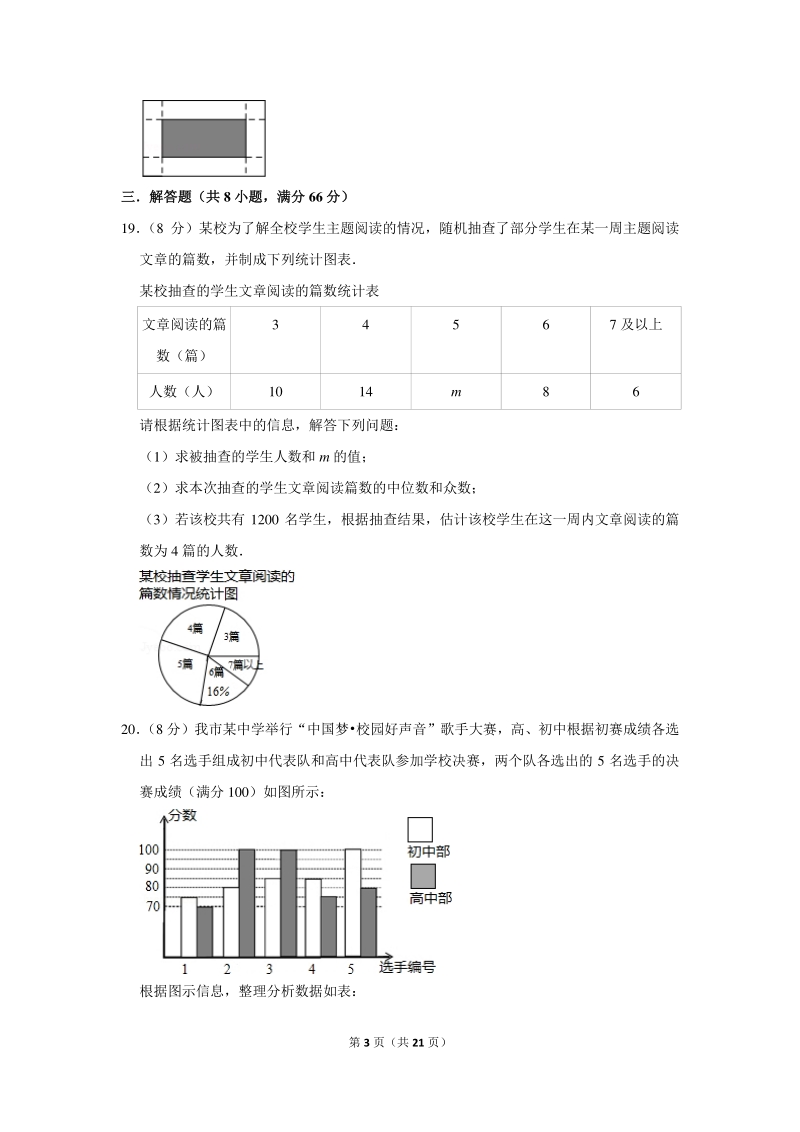
6、（3 分）如图，有一张矩形纸片，长 10cm，宽 6cm，在它的四角各剪去一个同样的小正 方形，然后将四周突出部分折起，就能制作一个无盖的方盒，若方盒的底面积（图中阴 影部分）是 32cm2，则剪去的小正方形的边长为   cm 第 3 页（共 21 页） 三解答题（共三解答题（共 8 小题，满分小题，满分 66 分）分） 19 （8 分）某校为了解全校学生主题阅读的情况，随机抽查了部分学生在某一周主题阅读 文章的篇数，并制成下列统计图表 某校抽查的学生文章阅读的篇数统计表 文章阅读的篇 数（篇） 3 4 5 6 7 及以上 人数（人） 10 14 m 8 6 请根据统计图表中的信息，

7、解答下列问题： （1）求被抽查的学生人数和 m 的值； （2）求本次抽查的学生文章阅读篇数的中位数和众数； （3）若该校共有 1200 名学生，根据抽查结果，估计该校学生在这一周内文章阅读的篇 数为 4 篇的人数 20 （8 分）我市某中学举行“中国梦校园好声音”歌手大赛，高、初中根据初赛成绩各选 出 5 名选手组成初中代表队和高中代表队参加学校决赛，两个队各选出的 5 名选手的决 赛成绩（满分 100）如图所示： 根据图示信息，整理分析数据如表： 第 4 页（共 21 页） 平均数（分） 中位数（分） 众数（分） 初中部 a 85 c 高中部 85 b 100 （1）求出表格中 a &nbs

8、p; ；b   ；c   （2）结合两队成绩的平均数和中位数，分析哪个队的决赛成绩较好； （3）计算两队决赛成绩的方差，并判断哪一个代表队选手成绩较为稳定 21 （8 分）解方程： （1）x22x+10 （2）2x23x+10 22 （8 分）解下列方程： （1）3x2+6x40； （2）3x（2x+1）4x+2 23 （8 分）汽车产业的发展，有效促进我国现代化建设某汽车销售公司 2016 年盈利 1500 万元，到 2018 年盈利 2160 万元，且从 2016 年到 2018 年，每年盈利的年增长率相同 （1）求每年盈利的年增长率； （2）若该公司盈利的年增长率继续

9、保持不变，那么 2019 年该公司盈利能否达到 2500 万 元？ 24 （8 分）已知关于 x 的一元二次方程 x2+（2k+1）x+k20 有实数根 （1）求 k 的取值范围 （2）设方程的两个实数根分别为 x1、x2，若 2x1x2x1x21，求 k 的值 25 （8 分）如图，在ABC 中，B90，AB5cm，BC7cm，点 P 从点 A 开始沿 AB 边向点 B 以 1cm/s 的速度移动，点 Q 从点 B 开始沿 BC 边向点 C 以 2cm/s 的速度移动 （1）如果 P，Q 分别从 A，B 同时出发那么几秒后，PQ 的长度等于cm？ （2）在（1）中，PQB 的面积能否等于 7

10、cm2？请说明理由 第 5 页（共 21 页） 26 （10 分）如果关于 x 的一元二次方程 ax2+bx+c0（a0）有两个实数根，且其中一个 根比另一个根大 1，那么称这样的方程为“邻根方程” 例如，一元二次方程 x2+x0 的 两个根是 x10，x21，则方程 x2+x0 是“邻根方程” （1）通过计算，判断下列方程是否是“邻根方程” ：x2x60；2x22x+1 0 （2）已知关于 x 的方程 x2（m1）xm0（m 是常数）是“邻根方程” ，求 m 的值；  （3）若关于 x 的方程 ax2+bx+10（a、b 是常数，a0）是“邻根方程” ，令 t8ab2， 问：存在多

11、少组 a、b 的值使得 t 为整数？请说明理由 第 6 页（共 21 页） 2019-2020 学年湖南省长沙市岳麓区麓山国际学校八年级（下）学年湖南省长沙市岳麓区麓山国际学校八年级（下） 月考数学试卷（月考数学试卷（3 月份）月份） 参考答案与试题解析参考答案与试题解析 一选择题（共一选择题（共 12 小题，满分小题，满分 36 分，每小题分，每小题 3 分）分） 1 （3 分）若一组数据 2，3，x，5，6，7 的众数为 7，则这组数据的中位数为（ ） A2 B3 C5.5 D7 【分析】根据众数的定义可得 x 的值，再依据中位数的定义即可得答案 【解答】解：数据 2，3，x，5，6，7

12、的众数为 7， x7， 把这组数据从小到大排列为：2、3、5、6、7、7， 则中位数为5.5； 故选：C 【点评】本题考查众数与中位数的意义中位数是将一组数据从小到大（或从大到小） 重新排列后，最中间的那个数（最中间两个数的平均数） ，叫做这组数据的中位数众数 是数据中出现最多的一个数 2 （3 分）为调查某班学生每天使用零花钱的情况，童老师随机调查了 30 名同学，结果如 下表： 每天使用零花 钱（单位：元）  5 10 15 20 25 人数 2 5 8 x 6 则这 30 名同学每天使用的零花钱的众数和中位数分别是（ ） A15、15 B20、17.5 C20、20 D20、1

13、5 【分析】利用众数的定义可以确定众数在第三组，由于随机调查了 20 名同学，根据表格 数据可以知道中位数是按从小到大排序，第 15 个与第 16 个数的平均数 【解答】解：童老师随机调查了 30 名同学， x3025869， 20 出现了 9 次，它的次数最多， 第 7 页（共 21 页） 众数为 20 随机调查了 30 名同学， 根据表格数据可以知道中位数（15+20）217.5，即中位数为 17.5 故选：B 【点评】本题属于基础题，考查了确定一组数据的中位数和众数的能力要明确定义， 一些学生往往对这个概念掌握不清楚，计算方法不明确而误选其它选项，注意找中位数 的时候一定要先排好顺序，然

14、后再根据奇数和偶数个来确定中位数，如果数据有奇数个， 则正中间的数字即为所求，如果是偶数个则找中间两位数的平均数 3 （3 分）在数据 1，3，5，7，9 中再添加一个数据，使得该组数据的平均数不变，则添加 的数据为（ ） A25 B3 C4.5 D5 【分析】根据平均数的公式求出数据 1，3，5，7，9 的平均数，根据题意可知添加的一 个数据是平均数，从而求解 【解答】解： （1+3+5+7+9）5 255 5 答：添加的数据为 5 故选：D 【点评】考查了算术平均数，平均数是指在一组数据中所有数据之和再除以数据的个 数它是反映数据集中趋势的一项指标 4 （3 分）某射击运动员练习射击，5

15、次成绩分别是：8、9、7、8、x（单位：环） ，下列说 法中正确的个数是（ ） 若这 5 次成绩的平均数是 8，则 x8； 若这 5 次成绩的中位数为 8，则 x8； 若这 5 次成绩的众数为 8，则 x8： 若这 5 次成绩的方差为 8，则 x8 A1 个 B2 个 C3 个 D4 个 【分析】 根据平均数的定义判断， 根据中位数的定义判断； 根据众数的定义判断； 根据方差的定义判断 第 8 页（共 21 页） 【解答】解：若这 5 次成绩的平均成绩是 8，则（8+9+7+8+x）8，解得 x8，故 本选项正确； 若这 5 次成绩的中位数为 8，则 x 为任意实数，故本选项错误； 若这 5

16、次成绩的众数是 8，则 x 为不是 7 与 9 的任意实数，故本选项错误； 如果 x8，则平均数为（8+9+7+8+8）8，方差为3（88）2+（98）2+（7 8）20.4，故本选项错误 故选：A 【点评】本题考查方差的定义与意义：一般地设 n 个数据，x1，x2，xn的平均数为 ， 则方差 S2（x1 ）2+（x2 ）2+（xn ）2，它反映了一组数据的波动大小， 方差越大，波动性越大，反之也成立同时考查了中位数、众数与平均数的定义 5 （3 分）已知1 是关于 x 的一元二次方程 ax2+bx+10 的一个根，则 ab 的值是 （ ）  A1 B0 C1 D2 【分析】把 x1

17、 代入一元二次方程 ax2+bx+10 即可得到 ab 的值 【解答】解：把 x1 代入一元二次方程 ax2+bx+10 得 ab+10， 所以 ab1 故选：A 【点评】本题考查了一元二次方程的解：能使一元二次方程左右两边相等的未知数的值 是一元二次方程的解 6 （3 分）利用配方法解一元二次方程 x26x+70 时，将方程配方为（xm）2n，则 m、 n 的值分别为（ ） Am9，n2 Bm3，n2 Cm3，n0 Dm3，n2 【分析】根据配方法的一般步骤先把常数项 7 移项后，应该在左右两边同时加上一次项 系数6 的一半的平方，即可得出答案 【解答】解：x26x+70， x26x7， x

18、26x+97+9， （x3）22， 则 m3，n2 故选：D 第 9 页（共 21 页） 【点评】此题考查了配方法的应用，掌握配方法的一般步骤是本题的关键，配方法的一 般步骤是（1）把常数项移到等号的右边； （2）把二次项的系数化为 1； （3）等式两边同 时加上一次项系数一半的平方 7 （3 分）方程 x（x5）x5 的根是（ ） Ax5 Bx0 Cx15，x20 Dx15，x21 【分析】利用因式分解法求解可得 【解答】解：x（x5）（x5）0， （x5） （x1）0， 则 x50 或 x10， 解得 x5 或 x1， 故选：D 【点评】本题主要考查解一元二次方程的能力，熟练掌握解一元二次

19、方程的几种常用方 法：直接开平方法、因式分解法、公式法、配方法，结合方程的特点选择合适、简便的 方法是解题的关键 8 （3 分）图中信息是小明和小华射箭的成绩，两人都射了 10 箭，则射简成绩的方差较大 的是（ ） A小明 B小华 C两人一样 D无法确定 【分析】根据图中的信息找出波动性小的即可 【解答】解：根据图中的信息可知，小华的成绩波动性小， 故射箭成绩的方差较大的是小华 故选：B 【点评】本题考查了方差的意义，方差是用来衡量一组数据波动大小的量，方差越大， 表明这组数据偏离平均数越大，即波动越大，数据越不稳定；反之，方差越小，表明这 组数据分布比较集中，各数据偏离平均数越小，即波动越小

20、，数据越稳定 第 10 页（共 21 页） 9 （3 分）有 5 人患了流感，经过两轮传染后共有 605 人患流感，则第一轮后患流感的人数 为（ ） A10 B50 C55 D45 【分析】设每轮传染中每人传染 x 人，根据经过两轮传染后共有 605 人患流感，即可得 出关于 x 的一元二次方程，解之即可得出 x 的值，取其正值代入（5+5x）中即可求出结 论 【解答】解：设每轮传染中每人传染 x 人， 依题意，得：5+5x+x（5+5x）605， 整理，得：x2+2x1200， 解得：x110，x212（不合题意，舍去） ， 5+5x55 故选：C 【点评】本题考查了一元二次方程的应用，找准

21、等量关系，正确列出一元二次方程是解 题的关键 10 （3 分）如果（m+2）x|m|+mx10 是关于 x 的一元二次方程，那么 m 的值为（ ） A2 或2 B2 C2 D0 【分析】根据一元二次方程的定义可得：|m|2，且 m20，再解即可 【解答】解：由题意得：|m|2 且 m+20， 解得：m2， 故选：B 【点评】此题主要考查了一元二次方程的定义，关键是掌握“未知数的最高次数是 2” ； “二次项的系数不等于 0” 11 （3 分）若关于 x 的一元二次方程（k+2）x22x10 有实数根，则实数 k 的取值范围 是（ ） Ak3 Bk3 Ck3 且 k2 Dk3 且 k2 【分析】

22、根据根的判别式即可求出答案 【解答】解：由题意可知：4+4（k+2）0， 解得：k3， k+20， k3 且 k2， 第 11 页（共 21 页） 故选：D 【点评】本题考查一元二次方程，解题的关键是熟练运用根的判别式，本题属于基础题 型 12 （3 分）设 a，b 是方程 x2+3x20170 的两个实数根，则 a2+2ab 的值为（ ） A2017 B2018 C2019 D2020 【分析】直接利用根与系数的关系得出 a+b 的值，再利用一元二次方程的根的意义得出 答案 【解答】解：a，b 是方程 x2+3x20170 的两个实数根， a2+3a20170，a+b3， 故 a2+3a20

23、17， 则 a2+2aba2+3a（a+b） 2017+3 2020 故选：D 【点评】此题主要考查了根与系数的关系，正确掌握相关性质是解题关键 二填空题二填空题（共（共 6 小题，满分小题，满分 18 分，每小题分，每小题 3 分）分） 13 （3 分）数据3，6，0，5 的极差为 9 【分析】根据极差的定义直接得出结论 【解答】解：数据3，6，0，5 的最大值为 6，最小值为3， 数据3，6，0，5 的极差为 6（3）9， 故答案为：9 【点评】此题考查了极差，极差反映了一组数据变化范围的大小，求极差的方法是用一 组数据中的最大值减去最小值 14 （3 分）某单位定期对员工按照专业能力、工

24、作业绩、考勤情况三方面进行考核（每项 满分 100 分） ，三者权重之比为 3：5：2小明经过考核后三项务数分别为 90 分，86 分、 83 分，则小明的最后得分为 86.6 分 【分析】将三个方面考核后所得的分数分别乘上它们的权重，再相加，即可得到最后得 分 【解答】解：小明的最后得分： 第 12 页（共 21 页） 90+86+8327+43+16.686.6（分） ， 故答案为：86.6 【点评】本题主要考查了加权平均数，数据的权能够反映数据的相对“重要程度” ，要突 出某个数据，只需要给它较大的“权” ，权的差异对结果会产生直接的影响 15 （3 分）已知样本数据 x1，x2，x3，

25、x4的方差为 2，则 4x1，4x2，4x3，4x4的方差是 32  【分析】列出两组数据的平均数和方差的式子，进行对比可得 【解答】解：样本 x1，x2，x3，x4的平均数 （x1+x2+x3+x4） ， 方差 s2（x1 ）2+（x2 ）2+（x3 ）2+（x4 ）2（x12+x22+x32+x42） 2 （x1+x2+x3+x4）+4 22， 新数据 4x1，4x2，4x3，4x4的平均数 2 （4x1+4x2+4x3+4x4）4 ， 方差 s22（4x14 ）2+（4x24 ）2+（4x34 ）2+（4x44 ）2 16（x12+x22+x32+x42）+216 （x1+x2

26、+x3+x4）+416 2 16（x12+x22+x32+x42）2 （x1+x2+x3+x4）+4 2 162 32 故答案为：32 【点评】此题主要考查了方差的计算一组数据都乘以 a，那么所得数据的方差是原数据 方差的 a 的平方倍 16 （3 分）若关于 x 的一元二次方程（x+a） 2b 有实数根，则 b 的取值范围是 b0  【分析】根据一元二次方程的解法即可求出答案 【解答】解：原方程化为（x+a）2b， b0， b0， 故答案为：b0 【点评】本题考查一元二次方程，解题的关键是熟练运用一元二次方程的解法，本题属 于基础题型 17 （3 分）若 a，b 是一元二次方程 x

27、22x+10 的两根，则 2 第 13 页（共 21 页） 【分析】根据根与系数的关系得出 a+b2，ab1，再根据，然后代值 计算即可得出答案 【解答】解：a，b 是一元二次方程 x22x+10 的两根， a+b2，ab1， 2 故答案为：2 【点评】本题考查了根与系数的关系：如果 x1，x2是一元二次方程 ax2+bx+c0（a0） 的两根，那么 x1+x2，x1x2 18 （3 分）如图，有一张矩形纸片，长 10cm，宽 6cm，在它的四角各剪去一个同样的小正 方形，然后将四周突出部分折起，就能制作一个无盖的方盒，若方盒的底面积（图中阴 影部分）是 32cm2，则剪去的小正方形的边长为

28、1 cm 【分析】设剪去的小正方形的边长为 xcm，根据矩形的面积公式结合方盒的底面积（图 中阴影部分） 是 32cm2， 即可得出关于 x 的一元二次方程， 解之取其较小值即可得出结论  【解答】解：设剪去的小正方形的边长为 xcm， 依题意，得： （102x） （62x）32， 整理，得：x28x+70， 解得：x11，x27（不合题意，舍去） 故答案为：1 【点评】本题考查了一元二次方程的应用，找准等量关系，正确列出一元二次方程是解 题的关键 三解答题（共三解答题（共 8 小题，满分小题，满分 66 分）分） 19 （8 分）某校为了解全校学生主题阅读的情况，随机抽查了部分学生

29、在某一周主题阅读 文章的篇数，并制成下列统计图表 某校抽查的学生文章阅读的篇数统计表 文章阅读的篇 数（篇） 3 4 5 6 7 及以上 第 14 页（共 21 页） 人数（人） 10 14 m 8 6 请根据统计图表中的信息，解答下列问题： （1）求被抽查的学生人数和 m 的值； （2）求本次抽查的学生文章阅读篇数的中位数和众数； （3）若该校共有 1200 名学生，根据抽查结果，估计该校学生在这一周内文章阅读的篇 数为 4 篇的人数 【分析】 （1）从统计图表可得， “阅读篇数为 6 篇”的有 8 人，占调查人数的 16%，可求 出调查人数；进而可求出阅读篇数为 5 篇的人数，即 m 的值

30、； （2）根据众数、中位数的意义，分别求出即可； （3）样本估计总体，样本中， “阅读篇数为 4 篇”占调查人数的，因此估计 1200 人 中，约有阅读篇数是 4 篇 【解答】解：816%50 人，m5010148612， 答：被抽查的学生人数 50 人，m 的值为 12； （2）学生阅读文章篇数出现次数最多的是 4 篇，出现 14 次，因此众数是 4 篇， 将学生阅读篇数从小到大排列处在第 25、26 位都是 5 篇，因此中位数是 5 篇， （3）1200336 人， 答：该校 1200 名学生中在这一周内文章阅读的篇数为 4 篇的有 336 人 【点评】考查扇形统计图、条形统计图的意义和制

31、作方法，从统计图中获取数量及数量 之间的关系是解决问题的关键，样本估计总体是统计中常用的方法 20 （8 分）我市某中学举行“中国梦校园好声音”歌手大赛，高、初中根据初赛成绩各选 出 5 名选手组成初中代表队和高中代表队参加学校决赛，两个队各选出的 5 名选手的决 赛成绩（满分 100）如图所示： 第 15 页（共 21 页） 根据图示信息，整理分析数据如表： 平均数（分） 中位数（分） 众数（分） 初中部 a 85 c 高中部 85 b 100 （1）求出表格中 a 85 ；b 80 ；c 85 （2）结合两队成绩的平均数和中位数，分析哪个队的决赛成绩较好； （3）计算两队决赛成绩的方差，并

32、判断哪一个代表队选手成绩较为稳定 【分析】 （1）根据平均数的计算公式和众数、中位数的定义分别进行解答，然后把表补 充完整即可； （2）根据平均数相同的情况下，中位数高的哪个队的决赛成绩较好； （3）根据方差公式先算出各队的方差，然后根据方差的意义即可得出答案 【解答】解： （1）初中代表队的平均成绩是： （75+80+85+85+100）585（分） ， 在初中代表队中 85 出现了 2 次，出现的次数最多，则众数是 85 分； 把高中代表队的成绩从小到大排列为：70，75，80，100，100，最中间的数是 80，则中 位数是 80 分； 填表如下： 平均数/分 中位数/分 众数/分 初中

33、代表 队 85 85 85 高中代表 队 85 80 100 故答案为：85，80，85； 第 16 页（共 21 页） （2）初中部成绩好些，因为两个队的平均数都相同，初中部的中位数高， 所以在平均数相同的情况下，中位数高的初中部成绩好些； （3）初中代表队的方差是：（7585）2+（8085）2+（8585）2+（8585）2+ （10085）270， 高中代表队的方差是：（7085）2+（7585）2+（8085）2+（10085）2+（100 85）2160， S初中 2S 高中 2， 初中代表队选手成绩较稳定 【点评】本题考查方差的定义：一般地设 n 个数据，x1，x2，xn的平均数

34、为 ，则方差 S2（x1 ）2+（x2 ）2+（xn ）2，它反映了一组数据的波动大小，方差 越大，波动性越大，反之也成立 21 （8 分）解方程： （1）x22x+10 （2）2x23x+10 【分析】 （1）利用因式分解法求解可得； （2）利用因式分解法求解可得 【解答】解： （1）x22x+10， （x1）20， 则 x1x21； （2）2x23x+10， （2x1） （x1）0， 则 2x10 或 x10， 解得 x0.5 或 x1 【点评】本题主要考查解一元二次方程的能力，熟练掌握解一元二次方程的几种常用方 法：直接开平方法、因式分解法、公式法、配方法，结合方程的特点选择合适、简便的

35、 方法是解题的关键 22 （8 分）解下列方程： 第 17 页（共 21 页） （1）3x2+6x40； （2）3x（2x+1）4x+2 【分析】 （1）根据公式法即可求出答案 （2）根据因式分解法即可求出答案 【解答】解： （1）a3，b6，c4， b24ac3643（4）840， 此方程有两个不相等的实数根， ， （2）3x（2x+1）2（2x+1） ， （2x+1） （3x2）0， 2x+10 或 3x20， 【点评】本题考查一元二次方程，解题的关键是熟练运用一元二次方程的解法，本题属 于基础题型 23 （8 分）汽车产业的发展，有效促进我国现代化建设某汽车销售公司 2016 年盈利 1

36、500 万元，到 2018 年盈利 2160 万元，且从 2016 年到 2018 年，每年盈利的年增长率相同 （1）求每年盈利的年增长率； （2）若该公司盈利的年增长率继续保持不变，那么 2019 年该公司盈利能否达到 2500 万 元？ 【分析】 （1）设该公司每年盈利的年增长率是 x，根据题意列出等量关系进行求解即可；  （2）相等关系是：2019 年盈利2018 年盈利（1+盈利年增长率） 【解答】解： （1）设每年盈利的年增长率为 x， 根据题意得：1500（1+x）22160 解得 x10.2，x22.2（不合题意，舍去） 答：每年盈利的年增长率为 20%； （2）216

37、0（1+0.2）2592，25922500 第 18 页（共 21 页） 答：2019 年该公司盈利能达到 2500 万元 【点评】此题考查了一元二次方程的应用，弄清题意是解本题的关键 24 （8 分）已知关于 x 的一元二次方程 x2+（2k+1）x+k20 有实数根 （1）求 k 的取值范围 （2）设方程的两个实数根分别为 x1、x2，若 2x1x2x1x21，求 k 的值 【分析】 （1）由0，求出 k 的范围； （2）由根与系数的关系可知：x1+x22k1，x1x2k2，代入等式求解即可 【解答】解： （1）一元二次方程 x2+（2k+1）x+k20 有实数根， （2k+1）24k20

38、， ； （2）由根与系数的关系可知： x1+x22k1，x1x2k2， 2x1x2x1x22k2+2k+11， k0 或 k1， ； k0 【点评】本题考查根与系数的关系；熟练掌握一元二次方程根与系数的关系，并能用判 别式判断根的存在情况是解题的关键 25 （8 分）如图，在ABC 中，B90，AB5cm，BC7cm，点 P 从点 A 开始沿 AB 边向点 B 以 1cm/s 的速度移动，点 Q 从点 B 开始沿 BC 边向点 C 以 2cm/s 的速度移动 （1）如果 P，Q 分别从 A，B 同时出发那么几秒后，PQ 的长度等于cm？ （2）在（1）中，PQB 的面积能否等于 7cm2？请说

39、明理由 【分析】 （1）根据 PQ52利用勾股定理 BP2+BQ2PQ2，求出即可； （2）由（1）得，当PQB 的面积等于 7cm2，然后利用根的判别式判断方程根的情况即 第 19 页（共 21 页） 可； 【解答】 （1）设 x 秒后，PQ2 BP5x  BQ2x BP2+BQ2PQ2 （5x）2+（2x）2（2）2 解得：x13，x21（舍去） 3 秒后，PQ 的长度等于 2； （2）PQB 的面积不能等于 7cm2，原因如下： 设 t 秒后，PB5t  QB2t 又SPQBBPQB7 （5t）2t7 t25t+70 52417252830 方程没有实数根 PQB 的

40、面积不能等于 7cm2 【点评】此题主要考查了一元二次方程的应用，找到关键描述语“PBQ 的面积等于 7m2” ，得出等量关系是解决问题的关键 26 （10 分）如果关于 x 的一元二次方程 ax2+bx+c0（a0）有两个实数根，且其中一个 根比另一个根大 1，那么称这样的方程为“邻根方程” 例如，一元二次方程 x2+x0 的 两个根是 x10，x21，则方程 x2+x0 是“邻根方程” （1）通过计算，判断下列方程是否是“邻根方程” ：x2x60；2x22x+1 0 （2）已知关于 x 的方程 x2（m1）xm0（m 是常数）是“邻根方程” ，求 m 的值；  （3）若关于 x

41、的方程 ax2+bx+10（a、b 是常数，a0）是“邻根方程” ，令 t8ab2， 问：存在多少组 a、b 的值使得 t 为整数？请说明理由 【分析】本题是一元二次方程的解法与新定义“邻根方程”的综合题，运用一元二次方 程的解法，结合新定义便可解答 （1）根据解一元二次方程的方法解出已知方程的解，再比较两根的差是否为 1，从而确 定方程是否为“邻根方程” ； 第 20 页（共 21 页） （2）先解方程求得其根，再根据新定义列出 m 的方程，注意有两种情况； （3）根据新定义得方程的大根与小根的差为 1，列出 a 与 b 的关系式，再由 t8ab2， 得 t 与 a 的关系，最后根据 t 为

42、整数，思考 a 的值，从而得出最后结果 【解答】解： （1）解方程得： （x3） （x+2）0， x3 或 x2， 23+1， x2x60 不是“邻根方程” ； x， ， 2x22x+10 是“邻根方程” ； （2）解方程得： （xm） （x+1）0， xm 或 x1， 方程 x2（m1）xm0（m 是常数）是“邻根方程” ， m1+1 或 m11， m0 或2； （3）解方程得，x， 关于 x 的方程 ax2+bx+10（a、b 是常数，a0）是“邻根方程” ， ， b2a2+4a， t8ab2， t4aa2， a0， a 为任意整数时，t 都为整数， 存在无数组 a、b 的值使得 t 为整数 【点评】本题考查一元二次方程，解题的关键是熟练运用一元二次方程的解法以及正确 第 21 页（共 21 页） 理解“邻根方程”的定义，本题属于中等题型