中考培优竞赛专题经典讲义 第31讲 几何三大变换之平移

《中考培优竞赛专题经典讲义 第31讲 几何三大变换之平移》由会员分享，可在线阅读，更多相关《中考培优竞赛专题经典讲义 第31讲 几何三大变换之平移（20页珍藏版）》请在七七文库上搜索。

1、第第 31 讲讲 几何三大变换之平移几何三大变换之平移 平移的性质 函数的平移变换 八字真言： “左加右减” ， “上加下减” 【例【例题讲解题讲解】 例题例题 1如图，将ABC沿BC方向平移得到DEF，若90B，6AB ，8BC ，2BE ，1.5DH ， 阴影部分的面积为 【解答】解：ABC沿BC方向平移得到DEF， 6DEAB， 1.5DH ， 61.54.5HEDEDH， 90B， 四边形ABEH是梯形， DEFCEHABCCEHABEH SSSSSS 阴影梯形 1 () 2 ABHE BE 1 (64.5)2 2 10.5 故答案为：10.5 平移的性质：ABC DEF 平移的距离：

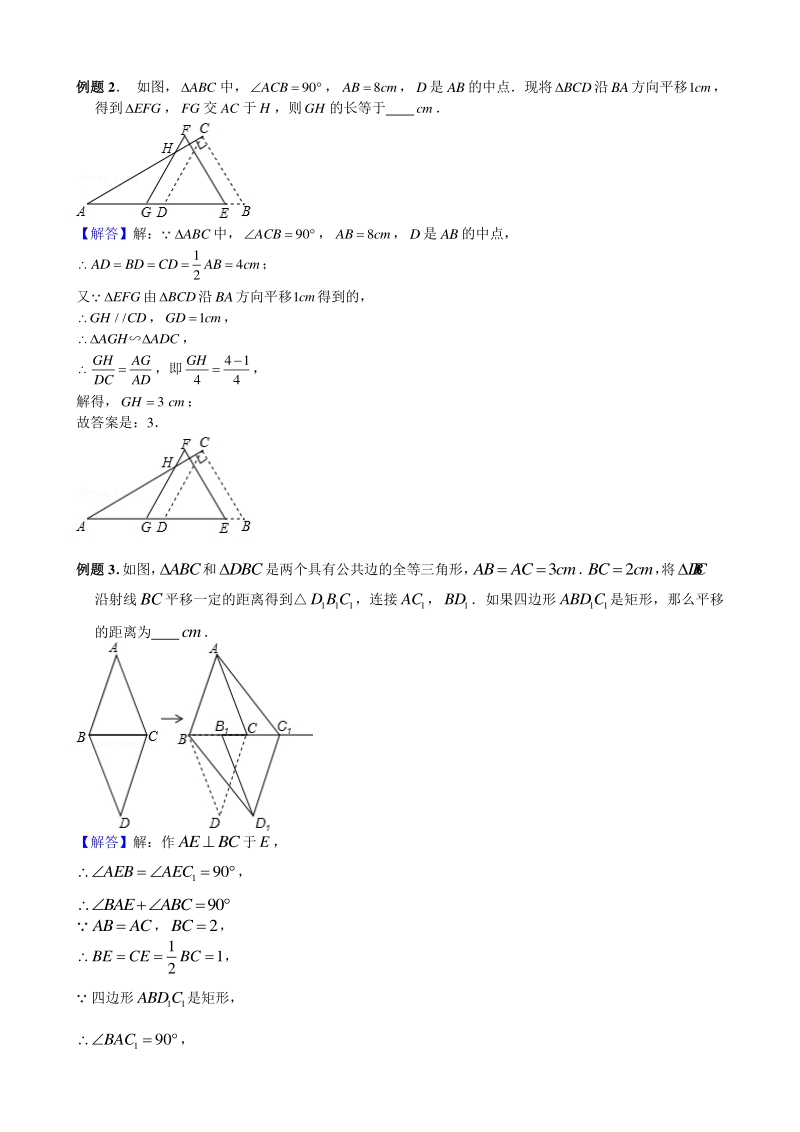
2、BE=CF=AD 平移的性质：ABC DEF 平移的距离：BE=CF=AD 平移的性质：ABC DEF 平移的距离：BE=CF=AD 四边形ABED、四边形BECF、 四边形ACFD均为平行四边形， 且S四边形ABED十S四边形BEFC=S四边形ACFD 例题例题 2 如图，ABC中，90ACB，8ABcm，D是AB的中点现将BCD沿BA方向平移1cm， 得到EFG，FG交AC于H，则GH的长等于 cm 【解答】解：ABC中，90ACB，8ABcm，D是AB的中点， 1 4 2 ADBDCDABcm； 又EFG由BCD沿BA方向平移1cm得到的， / /GHCD，1GDcm， AGHADC，

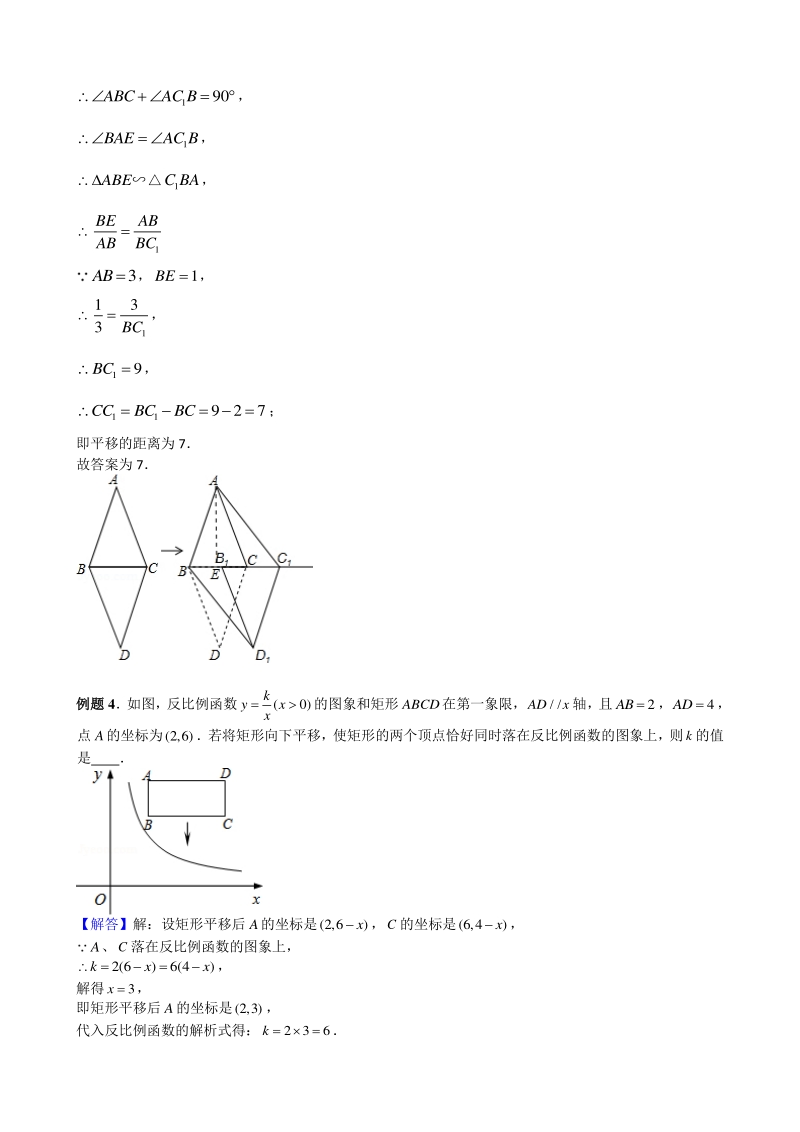
3、GHAG DCAD ，即 41 44 GH ， 解得，3GH cm； 故答案是：3 例题例题 3 如图，ABC和DBC是两个具有公共边的全等三角形，3ABACcm2BCcm， 将D B C 沿射线BC平移一定的距离得到 111 D BC，连接 1 AC， 1 BD如果四边形 11 ABDC是矩形，那么平移 的距离为 cm 【解答】解：作AEBC于E， 1 90AEBAEC， 90BAEABC ABAC，2BC ， 1 1 2 BECEBC， 四边形 11 ABDC是矩形， 1 90BAC， 1 90ABCAC B， 1 BAEAC B， ABE 1 C BA， 1 BEAB ABBC 3AB，

4、1BE ， 1 13 3BC ， 1 9BC， 11 927CCBCBC； 即平移的距离为 7 故答案为 7 例题例题 4如图，反比例函数(0) k yx x 的图象和矩形ABCD在第一象限，/ /ADx轴，且2AB ，4AD ， 点A的坐标为(2,6)若将矩形向下平移，使矩形的两个顶点恰好同时落在反比例函数的图象上，则k的值 是 【解答】解：设矩形平移后A的坐标是(2,6) x，C的坐标是(6,4) x， A、C落在反比例函数的图象上， 2(6)6(4)kxx ， 解得3x ， 即矩形平移后A的坐标是(2,3)， 代入反比例函数的解析式得：236k 故答案为 6 例题例题 5已知：如图，在矩

5、形ABCD中，5AB ， 20 3 AD ，AEBD，垂足是E点F是点E关于AB 的对称点， 连接AF、BF 若将ABF沿着射线BD方向平移， 设平移的距离为m（平移距离指点B沿BD 方向所经过的线段长度） 当点F分别平移到线段AB、AD上时，直接写出相应的m的值； 【解答】设平移中的三角形为A B F ，如答图 2 所示： 由对称点性质可知，12 由平移性质可知，/ /ABA B ，41 ，3BFB F 当点F落在AB上时， / /ABA B ， 34 ， 32 ， 3BBB F ，即3m ； 当点F落在AD上时， / /ABA B ， 62 ， 12 ，51 ， 56 ， 又易知ABAD

6、， B F D 为等腰三角形， 3B DB F ， 2516 3 33 BBBDB D ，即 16 3 m 例题例题 6已知二次函数 2 13 42 yxx 的图象如图将该抛物线沿它的对称轴向上平移，设平移后的抛物线 与x轴，y轴的交点分别为A、B、C三点，若90ACB，求此时抛物线的解析式 【解答】解：由 2 13 42 yxx 得：3 2 b x a ， (3,0)D；如图，设平移后的抛物线的解析式为 2 13 42 yxxk ， 则(0, )Ck，即OCk， 令0y ，即 2 13 0 42 xxk， 解得： 1 349xk， 2 349xk， (349Ak，0)，(349Bk，0)，

7、22 ( 493349)1636ABkkk ， 2222222 (349)(349)2836ACBCkkkkkk， 222 ACBCAB，即 2 28361636kkk， 解得： 1 4k ， 2 0k （舍去） ， 抛物线的解析式为 2 13 4 42 yxx 【巩固练习】【巩固练习】 1在直角坐标系中，一直线a向下平移 3 个单位后所得直线b经过点(0,3)A，将直线b绕点A顺时针旋转 60后所得直线经过点(3B ，0)，则直线a的函数关系式为 . 2若二次函数 y1=2（x+1）2-1 是由二次函数 y2=ax2+bx+c 先向右平移 2 个单位，再向上平移 1 个单位得到 的，则 a=

8、 ，b= ，c= . 3已知点P是二次函数 2 3yxx图象在y轴右侧部分上的一个动点，将直线2yx 沿y轴向上平移， 分别交x轴、y轴于C、D两点若以CD为直角边的PCD与OCD相似，则点P的坐标为 4如图，直线 4 3 yx与双曲线(0) k yx x 交于点A将直线 4 3 yx向右平移 9 2 个单位后，与双曲线 (0) k yx x 交于点B，与x轴交于点C，若2 AO BC ，则k 5如图，在平面直角坐标系中，已知点A坐标为(2,4)，直线2x 与x轴相交于点B，连结OA，二次函 数 2 yx图象从点O沿OA方向平移，与直线2x 交于点P，顶点M到A点时停止移动 （1）求线段OA所

9、在直线的函数解析式； （2）设二次函数顶点M的横坐标为m，当m为何值时，线段PB最短，并求出二次函数的表达式； （3）当线段PB最短时，二次函数的图象是否过点( ,1)Q a a ，并说理由 6如图，在平面直角坐标系中，直线24yx与y轴交于A点，与x轴交于B点，抛物线 2 1 1 : 4 Cyxbxc 过A、B两点，与x轴的另一交点为C （1）求抛物线解析式及C点坐标； （2）向右平移抛物线 1 C，使平移后的抛物线 2 C恰好经过BC的中点，求抛物线 2 C的表达式； 7如图， 已知抛物线经过点( 1,0)A 、(3,0)B、(0,3)C三点 （1） 该抛物线解析式为 ；顶点坐标为 ； （

10、2） 将该抛物线向下平移 3 个单位长度， 再向右移动(0)n n 个单位长度使得抛物线的顶点在ABC 内部 （不包括边界） ，试求n的取值范围； 8已知：如图，在直角梯形ABCD中，/ /ADBC，90B，2AD ，6BC ，3AB E为BC边 上一点，以BE为边作正方形BEFG，使正方形BEFG和梯形ABCD在BC的同侧 （1）当正方形的顶点F恰好落在对角线AC上时，求BE的长； （2）将（1）问中的正方形BEFG沿BC向右平移，记平移中的正方形BEFC为正方形B EFG，当点E与 点C重合时停止平移设平移的距离为t，正方形B EFG的边EF与AC交于点M，连接B D，B M， DM，是否

11、存在这样的t，使B DM是直角三角形？若存在，求出t的值；若不存在，请说明理由； （3）在（2）问的平移过程中，设正方形B EFG与ADC重叠部分的面积为S，请直接写出S与t之间的 函数关系式以及自变量t的取值范围 9如图，有一张直角三角形纸片ABC，90ACB，60B，3BC ，直角边AC在x轴上，B点在 第二象限，( 3A，0)，AB交y轴于E， 将纸片过E点折叠使BE与EA所在的直线上， 得到折痕(EF F 在x轴上） ，再展开还原沿EF剪开得到四边形BCFE，然后把四边形BCFE从E点开始沿射线EA方向 平行移动， 至B点到达A点停止 （记平移后的四边形为 1111) BC F E 在

12、平移过程中， 设平移的距离 1 BBx， 四边形 1111 BC FE与AEF重叠的面积为S （1）求折痕EF的长； （2）平移过程中是否存在点 1 F落在y轴上？若存在，求出x的值；若不存在，说明理由； （3）直接写出S与x的函数关系式及自变量x的取值范围 10如图，在平面直角坐标系xoy中，矩形ABCD的边AB在x轴上，且3AB ，2 3BC ，直线 32 3yx经过点C，交y轴于点G （1）求C，D坐标； （2）已知抛物线顶点32 3yx上，且经过点C，D的抛物线的解析式. （3）将（2）中抛物线沿直线32 3yx平移，平移后的抛物线交y轴于点F，顶点为点E（顶点在y 轴右侧） 平移后是

13、否存在这样的抛物线，使以 EF=EG 的EFG为等腰三角形？若存在，请求出此时抛 物线的解析式；若不存在，请说明理由 参考答案 1.【解答】解：设直线AB的解析式为ykxb，(0,3)A，(3B ，0)， 3 30 b kb ，解得 3 3 k b ， 直线AB的解析式为33yx由题意，知直线33yx绕点A逆时针旋转60后得到直线b， 则直线b经过(0,3)A，( 3，0)，易求直线b的解析式为33yx ，将直线b向上平移 3 个单位后 得直线a，所以直线a的解析式为333yx ，即36yx 2.【解答】a= 2 ，b= 12 ，c= 16 . 3.【解答】解：设(0,2 )Da，则直线CD解

14、析式为22yxa ， ( ,0)C a， :1:2OC OD， 2ODa，OCa， 根据勾股定理可得： 22 5CDOCODa 以CD为直角边的PCD与OCD相似， 当90CDP时，若:1:2PD DCOC OD，则 5 2 PDa， 设P的横坐标是x，则P点纵坐标是 2 3xx， 根据题意得： 2222 22222 5 (32 )() 2 5 ( 5 )()(3 )() 2 xxxaa aaxxxa ， 解得： 1 2 1 2 x a ， 则P的坐标是： 1 ( 2 ， 5) 4 ， 当90CDP时，若:1:2DC PDOC OD，同理可以求得(2,2)P， 当90DCP时，若:1:2PC

15、DCOC OD，则 11 ( 4 P， 11) 16 ， 当90DCP时，若:1:2DC PDOC OD，则 13 ( 5 P， 26) 25 故答案为： 1 ( 2 ， 5) 4 ，(2,2)， 11 ( 4 ， 11) 16 ， 13 ( 5 ， 26) 25 4.【解答】解：设点A的坐标为 4 ( ,) 3 aa， 2 AO BC ， 取OA的中点D， 点B相当于点D向右平移了 9 2 个单位， 点D的坐标为 1 ( 2 a， 2 ) 3 a， B点坐标为 91 ( 22 a， 2 ) 3 a， 点A，B都在反比例函数 k y x 的图象上， 4291 () 3322 aaaa ， 解得

16、3a 或0(0不合题意，舍去） 点A的坐标为(3,4)， 12k 5.【解答】解： （1）设直线OA的解析式为ykx， (2,4)A， 24k，解得2k ， 线段OA所在直线的函数解析式为2yx； （2）顶点M的横坐标为m，且在OA上移动， 2 (02)ymm剟， ( ,2 )M mm， 抛物线的解析式为 2 ()2yxmm， 当2x 时， 22 (2)224(02)ymmmmm剟， 22 24(1)3(02)PBmmmm剟， 当1m 时，PB最短， 当PB最短时，抛物线的解析式为 2 (1)2yx； （3）若二次函数的图象是过点( ,1)Q a a 则方程 2 1(1)2aa 有解 即方程

17、2 340aa有解， 2 ( 3)4 1 470 二次函数的图象不过点Q 6.【解答】解： （1）直线24yx与y轴交于A点，与x轴交于B点， 令0x ，可得4y ，则点A的坐标为(0,4)A， 令0y ，可得2x ，则点B的坐标为( 2,0)， 将(0,4)A，( 2,0)B 代入 2 1 4 yxbxc ， 可得 4 1 042 4 c bc 解得 3 2 4 b c 抛物线 1 C的解析式为： 2 13 4 42 yxx ， 令0y ，则 2 13 40 42 xx， 解得8x ， C点坐标为(8,0)； （2）由（1）知，( 2,0)B ，(8,0)C 设BC的中点为G，则(3,0)G

18、 22 13125 4(3) 4244 yxxx ， 平移后抛物线的解析式为： 2 125 (8) 44 yx ； 7.【解答】解： （1） 设抛物线为 2 (0)yaxbxc a， 将( 1,0)A 、(3,0)B、(0,3)C代入得 0 930 3 abc abc c ， 解得： 1 2 3 a b c 故抛物线解析式为： 2 23yxx ， 22 23(1)4yxxx ， 故顶点坐标为(1,4)； 故答案为： 2 23yxx ，(1,4)； （2） 由 （1） 得， 22 23(1)4yxxx ， 平移后的抛物线为： 22 (1)43(1)1yxnxn ， 平移后的抛物线顶点为(1,1)

19、n， 设直线BC的解析式为：ymxn， 将(3,0)B、(0,3)C代入得 30 3 mn n ， 解得： 1 3 m n ， 直线BC的解析式为3yx ， 当1y 时，2x， 1 12n ， 01n ， 8.【解答】解： （1）如图， 设正方形BEFG的边长为x， 则BEFGBGx， 3AB ，6BC ， 3AGABBGx， / /GFBE， AGFABC， AGGF ABBC ， 即 3 36 xx ， 解得：2x ， 即2BE ； （2）存在满足条件的t， 理由：如图，过点D作DHBC于H， 则2BHAD，3DHAB， 由题意得：BBHEt ，|2|HBt，4ECt， / /EFAB，

20、MECABC， MEEC ABBC ，即 4 36 MEt ， 1 2 2 MEt， 在RtB ME中， 222222 11 2(2)28 24 B MMEB Ettt， 在Rt DHB中， 222222 3(2)413B DDHB Httt ， 过点M作MNDH于N， 则MNHEt， 1 2 2 NHMEt， 11 3(2)1 22 DNDHNHtt， 在Rt DMN中， 2222 5 1 4 DMDNMNtt ， （）若90DB M，则 222 DMBMB D ， 即 222 51 1(28)(413) 44 tttttt ， 解得： 20 7 t ， （）若90B MD ，则 222 B

21、 DBMDM ， 即 222 15 413(28)(1) 44 tttttt ， 解得： 1 317t ， 2 317t （舍去） ， 317t ； （）若90B DM ，则 222 BMB DDM ， 即： 222 15 28(413)(1) 44 tttttt ， 此方程无解， 综上所述，当 20 7 t 或317 时，B DM是直角三角形； （3）如图，当F在CD上时，:EF DHCE CH， 即2:3:4CE， 8 3 CE， 84 62 33 tBBBCB EEC ， 1 2 2 MEt， 1 2 FMt， 当 4 0 3 t剟时， 2 111 224 FMN SSttt ， 如图，

22、当G在AC上时，2t ， 33 tan(4)3 44 DH EKECDCBECtt CH ， 3 21 4 FKEKt， 24 33 NLAD， 4 3 FLt ， 当 4 2 3 t 时， 22 114312 ()(1) 423483 FMNFKL SSSttttt ； 如图，当G在CD上时，:B C CHB G DH， 即:42:3B C， 解得： 8 3 B C， 2 42 3 ECtB C ， 10 3 t ， 111 (6)3 222 B NB Ctt， 1 1 2 GNGBB Nt， 当 10 2 3 t 时， 2 11114335 2112 22223483 FKLGNMF SS

23、Stttttt 梯形 ， 如图，当 10 4 3 t 时， 33 (6) 44 B LB Ct， 33 (4) 44 EKECt， 11 (6) 22 B NB Ct， 11 (4) 22 EMECt， 15 22 MNLKB EKLB EMN SSSSt 梯形梯形梯形 综上所述： 当 4 0 3 t剟时， 2 1 4 St， 当 4 2 3 t 时， 2 12 83 Stt ； 当 10 2 3 t 时， 2 35 2 83 Stt ， 当 10 4 3 t 时， 15 22 St 9.【解答】解： （1）90ACB，60B， 30BAC， ( 3A，0)， 1EO， 60EFO，90EOF

24、， 2 3 sin603 EO EF ， （2）存在，理由如下： 如图 1，作 1 B DBC， 3 3 FO ， 1 3 3 B D，60B 1 1 2 sin603 B D BB ，即 2 3 x ， （3）当02x剟时，即点E到A时经过的面积，如图 2， 3AO ，90ACB，60B， 2AE， 11 BBEEx， 1 2E Ax， 1 3 (2) 3 E Mx， 2 11 11 2 3332 3 ()(2) 223363 SEFE ME Exxxx 当 10 2 3 x 时，S为AEF的面积， 所以 112 32 3 2 2233 SEF AE， 当104 3 x 时，如图 3 90A

25、CB，60B，3BC ， 3 3AC， 3AO ， 3 3 OF ， 35 3 3 33 33 CF， 此时 1 10 3 BB ，即当 11 BC过点F时 10 3 x ， 当 10 3 x 时， 310 () 23 FMx，在RT NMF中， 310 3() 23 NMFMx， NMF的面积为： 11310310 ()() 222323 FM MNxx， 2 2 313103103 357 3 ()() 322323822 AEFNMF SSSxxxx ， 当46x 时，如图 4， 90ACB，60B，3BC ， 6AB， 1 6ABx， 1 1 (6) 2 DBx， 3 (6) 2 AD

26、x， 2 1 111333 39 3 (6)(6) 2222822 SDA DBxxxx， 综上可知S与x的函数关系式为： 2 2 2 32 3 (02) 63 2 310 (2) 33 3 357 3 10 (4) 8223 33 39 3 (46) 822 xxx x S xxx xxx 剟 ， 故答案为： 2 2 2 32 3 (02) 63 2 310 (2) 33 3 357 3 10 (4) 8223 33 39 3 (46) 822 xxx x S xxx xxx 剟 10.【解答】解： （1）令2 3y ，2 332 3x，解得4x ， 则431OA， (4C，2 3)，(1D

27、，2 3)； （2）由二次函数对称性得，顶点横坐标为1 45 22 ， 令 5 2 x ，则 53 32 3 22 y ， 顶点坐标为 5 ( 2 ， 3) 2 ， 设抛物线解析式为 2 53 () 22 ya x，把点(1D，2 3)代入得， 2 3 3 a ， 解析式为 2 2 353 () 322 yx， 即 2 2 310 314 3 333 yxx， （3）设顶点E在直线上运动的横坐标为m，则(E m，32 3)(0)mm 可设解析式为 2 2 3 ()32 3 3 yxmm， 若GEEF时，2 3FGm，则(0F，2 32 3)m， 代入解析式得： 2 2 3 32 32 32 3 3 mmm，解得0m （舍去） ， 3 2 m ， 此时所求的解析式为： 2 2 333 () 322 yx；