中考培优竞赛专题经典讲义 第14讲 数学基本方法之等积法

《中考培优竞赛专题经典讲义 第14讲 数学基本方法之等积法》由会员分享，可在线阅读，更多相关《中考培优竞赛专题经典讲义 第14讲 数学基本方法之等积法（15页珍藏版）》请在七七文库上搜索。

1、第第 1 14 4 讲讲 数学基本方法之等积法数学基本方法之等积法 在解决几何问题时，通常可采用等积法来解决一些问题，即同一个图形采用不同的面积表示方法来建立等 式.等积法也常在证明某些定理时被用到. 【例题讲解】【例题讲解】 例题例题 1 已知：如图，在 RtABC中，BAC90，AB4，AC3，ADBC，求 AD 的长为 DCB A 答案： AD2.4. 例题例题 2、如图，E是边长为 1 的正方形 ABCD 的对角线上一点，且 BEBC，P为 CE上任意一点，PQBC 于点 Q，PRBE 于点 R，则 PQPR 的值为 . R Q P E D CB A 答案： 2 2 . 【解析】连接

2、BP，易知 BEC S BEP S BCP S，所以 1 2 BECM 1 2 BEPR 1 2 BCPQ，由 BC BE，等号两边同时约掉，剩下 CMPRPQ，所以 CM 2 2 BC 2 2 . 连接 BP，过 C作 CMBD， BEC S BEP S BCP S BCPQ 1 2 BEPR 1 2 BC（PQPR） 1 2 BECM 1 2 ， BCBE， PQPRCM， BEBC1，且正方形对角线 BD2BC2， 又BCCD，CMBD， M为 BD中点，又BDC为直角三角形， CM 1 2 BD 2 2 ， 即 PQPR 值是 2 2 M R Q P E D CB A 【对于填空选择题

3、，可用特殊值法！ 】【对于填空选择题，可用特殊值法！ 】 例题例题 3 如图，正方形 ABCD 的边长为 1，点 P为边 BC 上任意一点（可与 B 点或 C 点重合） ，分别过 B、 C、D 作射线 AP 的垂线，垂足分别是B、C、D，则 BBCCDD的最大值为 ，最小值 为 P B C D D C B A 答案：2，2. 【解析】连接 AC、DP， ABCD S正方形111， 由勾股定理得：AC 22 112， AB1， 1AP2， DPC S APC S 1 2 APCC， 1 ABCD S正方形 ABP S ADP S DPC S 1 2 AP（BBCCDD） ， BBCCDD 2 A

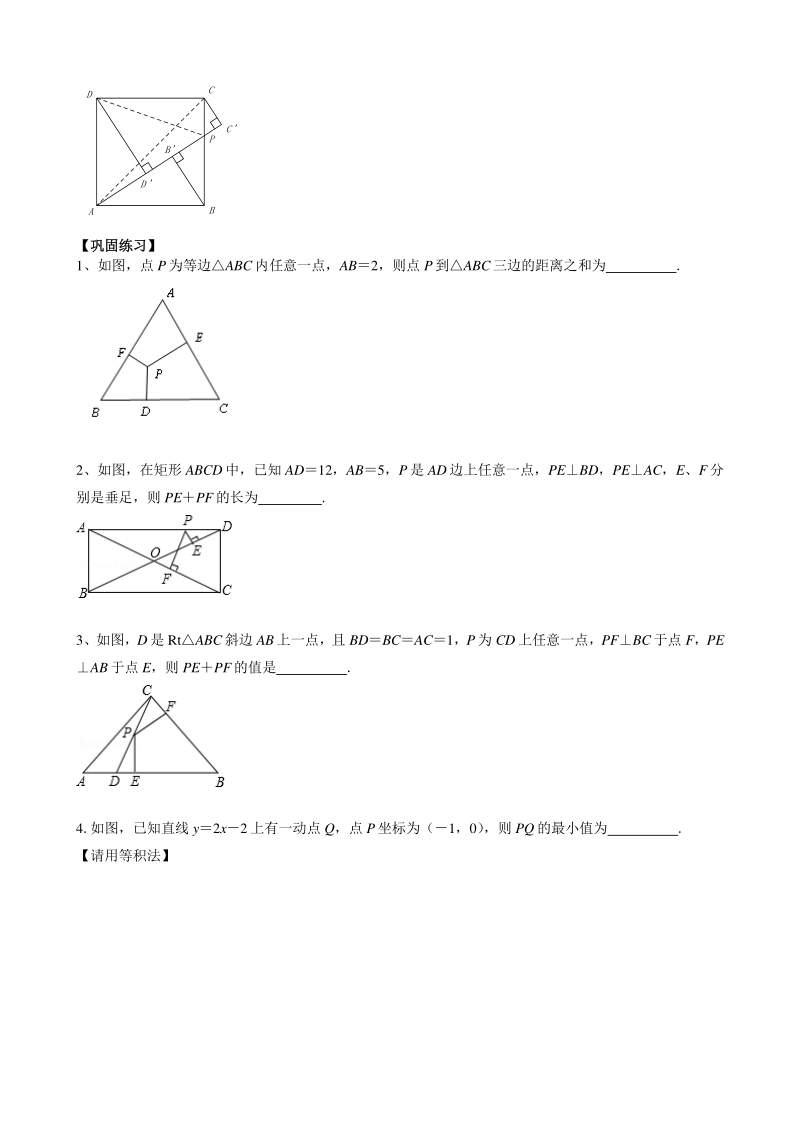
4、P ， 1AP2， 2BBCCDD2， P B C D D C B A 【巩固练习】【巩固练习】 1、如图，点 P 为等边ABC 内任意一点，AB2，则点 P到ABC三边的距离之和为 . 2、如图，在矩形 ABCD中，已知 AD12，AB5，P是 AD边上任意一点，PEBD，PEAC，E、F分 别是垂足，则 PEPF的长为 . 3、如图，D 是 RtABC斜边 AB上一点，且 BDBCAC1，P为 CD上任意一点，PFBC 于点 F，PE AB 于点 E，则 PEPF的值是 . 4.如图，已知直线 y2x2 上有一动点 Q，点 P坐标为（1，0） ，则 PQ的最小值为 . 【请用等积法】 5.

5、如图，在 RtABC中，ABC90，点 D是斜边上的中点，点 P 在 AB上，PEBD于 E，PFAC 于 F，若 AB6，BC3.，则 PEPF . P F E D C B A 6.将两个全等的直角三角形按图 1所示摆放，其中DAB90，求证：abc. 7如图，在ABC中， A90，D 是 AC 上的一点，BDDC，P 是 BC 上的任一点，PEBD，PF AC，E、F为垂足求证：PEPFAB P F E D C B A 8如图，平行四边形ABCD中，AB: BC3:2，DAB60，E在AB上，且 AE: EB1:2，F 是BC的中点，过D分别作 DPAF于P，DQCE 于Q，求证： DPC

6、E DQAF Q P F E D C BA 图 4 图 5 9.在ABC中，AB13，BC14 （1）如图 1，ADBC于点 D，且 BD5，则ABC的面积为 ； （2）在（1）的条件下，如图 2，点 H是线段 AC 上任意一点，分别过点 A，C作直线 BH的垂线，垂足为 E，F，设 BHx，AEm，CFn，请用含 x的代数式表示 mn，并求 mn的最大值和最小值 DCB A H F E DCB A 10 【问题情境】【问题情境】 张老师给爱好学习的小军和小俊提出这样一个问题：如图 1，在ABC 中，ABAC，点 P为边 BC上的任 一点，过点 P 作 PDAB，PEAC，垂足分别为 D、E，

7、过点 C 作 CFAB，垂足为F求证：PDPE CF F E P D CB A F G E P D CB A E F A B C D P 小军的证明思路是：如图 2，连接 AP，由ABP 与ACP 面积之和等于ABC的面积可以证得：PDPE CF 小俊的证明思路是：如图 2，过点 P 作 PGCF，垂足为 G，可以证得：PDGF，PECG，则 PDPE CF 【变式探究】【变式探究】 图 1 图 2 图 1 图 2 图 3 如图 3，当点 P在 BC延长线上时，其余条件不变，求证：PDPECF； 请运用上述解答中所积累的经验和方法完成下列两题： 【结论运用】【结论运用】 如图 4，将矩形 AB

8、CD沿 EF 折叠，使点 D 落在点 B上，点 C 落在点 C 处，点 PP为折痕 EF上的任一点， 过点 P作 PGBE、PHBC，垂足分别为 G、H，若 AD8，CF3，求 PGPH的值； C P H G F E D CB A 【迁移拓展】【迁移拓展】 图 5是一个航模的截面示意图在四边形 ABCD中，E为 AB 边上的一点，EDAD，ECCB，垂足分别 为 D、C，且 ADCEDEBC，AB2 3dm，AD3dm，BD37dmM、N 分别为 AE、BE的中点， 连接 DM、CN，求DEM与CEN的周长之和 NME D C BA 图 5 图 4 参考答案 1.答案：3. 2.答案： 60

9、13 . 3.答案： 2 2 . 【解析】如图所示，过C作CHAB于H，D是Rt ABC斜边AB上一点，且1BDBCAC， 2 2 CH， 112 12 222 BDC SBD CH ， 又 1111 11 2222 BCDBPCBPD SSSBD PEBC PFPEPF ， 2 2 PEPF H P F ED C B A 4.答案： 4 5 5 . 【解析】如图，过点 P 作 PQAB于点 Q，过点 Q作 QCQB，则 y2x2 A（0，2） ，B（1，0） PQBAOB BQ OB PB AB AB 22 OBOA5，PB2，OB1 1 BQ 2 5 BQ 2 5 5 PQ 22 PBBQ

10、 2 2 5 4 5 16 5 4 5 5 . 5.答案： 6 5 5 . 如图作 BMAC于 M，连接 PD MP F E D C B A ABC90，ADDC，AB6，BC3， BDADDC，AC 22 ABBC3 5， 1 2 ABBC 1 2 ACBM， BM 6 5 5 ， ABD S ADP S BDP S， 1 2 ADBM 1 2 ADPF 1 2 BDPE， PEPFBM 6 5 5 MP F E D C B A 6.答案：连接 DB，过点 D作 BC边上的高 DF，则 DFECba ADCB S四边形 ACD S ABC S 1 2 b 1 2 ab 又 ADCB S四边形

11、 ADB S DCB S 1 2 c 1 2 a（ba） 1 2 b 1 2 ab 1 2 c 1 2 a（ba） abc. F E D C B A c b a c b a F c b a c b a E D C B A 请参照上述请参照上述证法，利用图证法，利用图 2证明：证明：abc 【解析】连结 BD，过点 B作 DE边上的高 BF，可得 BFba， ACBED S五边形 ACB S ABE S ADE S 1 2 ab 1 2 b 1 2 ab， 又 ACBED S五边形 ACB S ABD S BDE S 1 2 ab 1 2 c 1 2 a（ba） ， 1 2 ab 1 2 b 1

12、 2 ab 1 2 ab 1 2 c 1 2 a（ba） ， abc. 图 1 图 2 F c b a c b a E D C B A 7.【解析】过 P作 PGAB于 G，交 BD于 O， PFAC，A90， AAGPPFA90， 四边形 AGPF 是矩形， AGPF，PGAC， BDDC， CGPBDBP， OBOP， PGAB，PEBD， BGOPEO90， 在BGO和PEO 中 BGOPEO GOBEOP OBOP BGOPEO， PEBG， ABBGAG， PEPFAB G O P F E D C B A 8.【解析】连接 DE、DF， 根据三角形的面积和平行四边形的面积得： 1 2

13、 DECDFAABCD SSS 平行四边形 ， 即 1 2 AFDF 1 2 CEDQ， AFDPCEDQ， DPCE DQAF . Q P F E D C B A 9.【解析】 （1）在 RtABD中，AB13，BD5， AD 22 ABBD 22 13512. BC14， ABC S 1 2 BCAD 1 2 141284. 故答案为：84 （2） ABC S ABH S BHC S， 1 2 BHAE 1 2 BHCF84 xmxn168. mn 168 x AD12，DC1459， AC 22 ADCD15， mn与 x 成反比， 当 BHAC 时，mn 有最大值 （mn）BHACBH

14、 mnAC15. mn与 x 成反比， 当 BH 值最大时，mn有最小值 当点 H 与点 C 重合时 mn有最小值 mn 168 14 ， mn等于 12. mn的最大值为 15，最小值为 12 10.【解析】 【问题情境】【问题情境】 证明： （小军的方法）连接 AP，如图 PDAB，PEAC，CFAB， 且 ABC S ABP S ACP S， 1 2 ABCF 1 2 ABPD 1 2 ACPE. ABAC， CF PDPE （小俊的方法）过点 P 作 PGCF，垂足为 G，如图 PDAB，CFAB，PGFC， CFDFDPFGP90 四边形 PDFG是矩形 DPFG，DPG90. CG

15、P90 PEAC， CEP90， PGCCEP. BDPDPG90， PGAB. GPCB. ABAC， BACB. GPCECP. 在PGC和CEP 中， PGCCEP GPCECP PCCP PGCCEP. CGPE. CFCGFG PEPD G E P F D CB A 【变式探究】【变式探究】 证明：连接 AP，如图 PDAB，PEAC，CFAB， 且 ABC S ABP S ACP S， 1 2 ABCF 1 2 ABPD 1 2 ACPE. ABAC， CFPDPE. G E F A B C D P 【结论运用】【结论运用】 过点 E作 EQBC，垂足为 Q，如图， 四边形 ABC

16、D是矩形， ADBC，CADC90. AD8，CF3， BFBCCFADCF5. 由折叠可得：DFBF，BEFDEF DF5. C90， DC 22 DFCF 22 53 4. EQBC，CADC90， EQC90CADC. 四边形 EQCD是矩形. EQDC4. ADBC， DEFEFB. BEFDEF， BEFEFB. BEBF. 由问题情境中的结论可得：PGPHEQ PGPH4. PGPH的值为 4. Q C P H G F E D CB A 【迁移拓展】【迁移拓展】 延长 AD、BC 交于点 F，作 BHAF，垂足为 H，如图 ADCEDEBC， AD DE BC EC . EDAD，

17、ECCB， ADEBCE90. ADEBCE. ACBE. FAFB. 由问题情境中的结论可得：EDECBH 设 DHxdm， 则 AHADDH（3x）dm BHAF， BHA90. BHBDDHABAH. AB2 13，AD3，BD37， （37）x（2 13）（3x）. 解得：x1 BHBDDH37136. BH6dm. EDEC6. ADEBCE90， 且 M、N分别为 AE、BE的中点， DMAMEM 1 2 AE，CNBNEN 1 2 BE. DEM 与CEN的周长之和 DEDMEMCNENEC DEAEBEEC DEABEC DEECAB 62 3 DEM 与CEN的周长之和为（62 3）dm. F H NME D C BA