中考培优竞赛专题经典讲义 第10讲最值问题之三角形三边关系

《中考培优竞赛专题经典讲义 第10讲最值问题之三角形三边关系》由会员分享，可在线阅读，更多相关《中考培优竞赛专题经典讲义 第10讲最值问题之三角形三边关系（19页珍藏版）》请在七七文库上搜索。

1、第第 1010 讲讲 最值问题之三角形三边关系最值问题之三角形三边关系 模型讲解模型讲解 问题：在直线 l 上找一点 P，使得PAPB的值最大 解析：连接 AB，并延长与 1 交点即为点 P. 证明：如图，根据ABP三边关系，BP-AP0Q+QP QPQP 所以连接 OP，与圆的交点即为所求点 Q，此时 PQ 最短. 【另外三种情况】 点 P 在圆外，PQ 最长 点 P 在圆内，PQ 最长 点 P 在圆内，PQ 最短 【总结】可见，点与圆的最值问题在本质上仍然是利用了三角形三边关系。 【例题讲解】【例题讲解】 例题例题 1、如图，在矩形 ABCD 中，AB=4，AD=6，E 是 AB 边的中点

2、，F 是线段 BC 边上的动点，将EBF 沿 EF 所在直线折叠得到EBF，连接 BD，则 BD 的最小值是_. 【解析】 如图，根据已知条件，在EBD 中，我们发现，EB为定值 2，ED 根据勾股定理计算可得也为定值 2 10，而 BD 即为要我们求的那条边，所以我们就知道，EBD 就是我们要找的三角形， BDED-EB 当 B在 ED 上时，BD 最小 BD 的最小值为2 10-2 【巩固练习】【巩固练习】 1、如图，在 RtABC 中，ACB=90，AC=BC=2，以 BC 为直径的半圆交 AB 于 D，P 是弧 CD 上的一 个动点，连接 AP，则 AP 的最小值是_. 2、如图，在平

3、面直角坐标系中，已知点 A（1，0） ，B（1-a，0） ，C（1+a，0） （a0） ，点 P 在以 D（4，4） 为圆心，1 为半径的圆上运动，且始终满足BPC=90，则 a 的最大值_. 3、如图，在ABC 中，AB=10，AC=8，BC=6，以边 AB 的中点 O 为圆心，作半圆与 AC 相切，点 P，Q 分别是边 BC 和半圆上的动点，连接 PQ，则 PQ 长的最大值与最小值的和是_. 4、如图，已知直线 y= 3 4 x-3 与 x 轴、y 轴分别交于 A、B 两点，P 是以 C（0，1）为圆心，1 为半径的圆上 一动点，连结 PA、PB.则PAB 面积的最大值是_. 5、如图，在

4、ABC 中，ACB=90，AB=5，BC=3，P 是 AB 边上的动点（不与点 B 重合） ，将BCP 沿 CP 所在的直线翻折，得到BCP，连接 BA，则 BA 长度的最小值是_. 6、如图，在平行四边形 ABCD 中，BCD=30，BC=4，CD=33，M 是 AD 边的中点，N 是 AB 边上的 一动点，将AMN 沿 MN 所在直线翻折得到AMN，连接 AC，则 AC 长度的最小值是_. 7、如图，菱形 ABCD 中，A=60，AB=3，A、B 的半径分别为 2 和 1，P、E、F 分别是边 CD、 A 和B 上的动点，则 PE+PF 的最小值是_. 8、如图，矩形 ABCD 中，AB=

5、2，AD=3，点 E、F 分别为 AD、DC 边上的点，且 EF=2，点 G 为 EF 的中 点，点 P 为 BC 上一动点，则 PA+PG 的最小值为_. 9、如图，边长为 1 的正方形 ABCD 中，以 A 为圆心，1 为半径作BD，将一块直角三角板的直角顶点 P 放置在BD（不包括端点 B、D）上滑动，一条直角边通过顶点 A，另一条直角边与边 BC 相交于点 Q，连 接 PC，则CPQ 周长的最小值为_. 10、问题情境：如图 1，P 是0 外的一点，直线 PO 分别交0 于点 A、B，则 PA 是点 P 到0 上的点的 最短距离. （1）探究：）探究： 如图 2，在0 上任取一点 C（

6、不为点 A、B 重合） ，连接 PC、OC.试证明：PAPC. （2）直接运用：）直接运用：如图 3，在 RtABC 中，ACB=90，AC=BC=2，以 BC 为直径的半圆交 AB 于 D， P 是CD上的一个动点，连接 AP，则 AP 的最小值是_. （3）构造运用：）构造运用：如图 4，在边长为 2 的菱形 ABCD 中，A=60，M 是 AD 边的中点，N 是 AB 边上 一动点，将AMN 沿 MN 所在的直线翻折得到AMN，连接 AC，请求出 AB 长度的最小值. 解：由折叠知 AM=AM，又 M 是 AD 的中点，可得 MA=MA=MD，故点 A在以 AD 为直径的圆上. （请继续

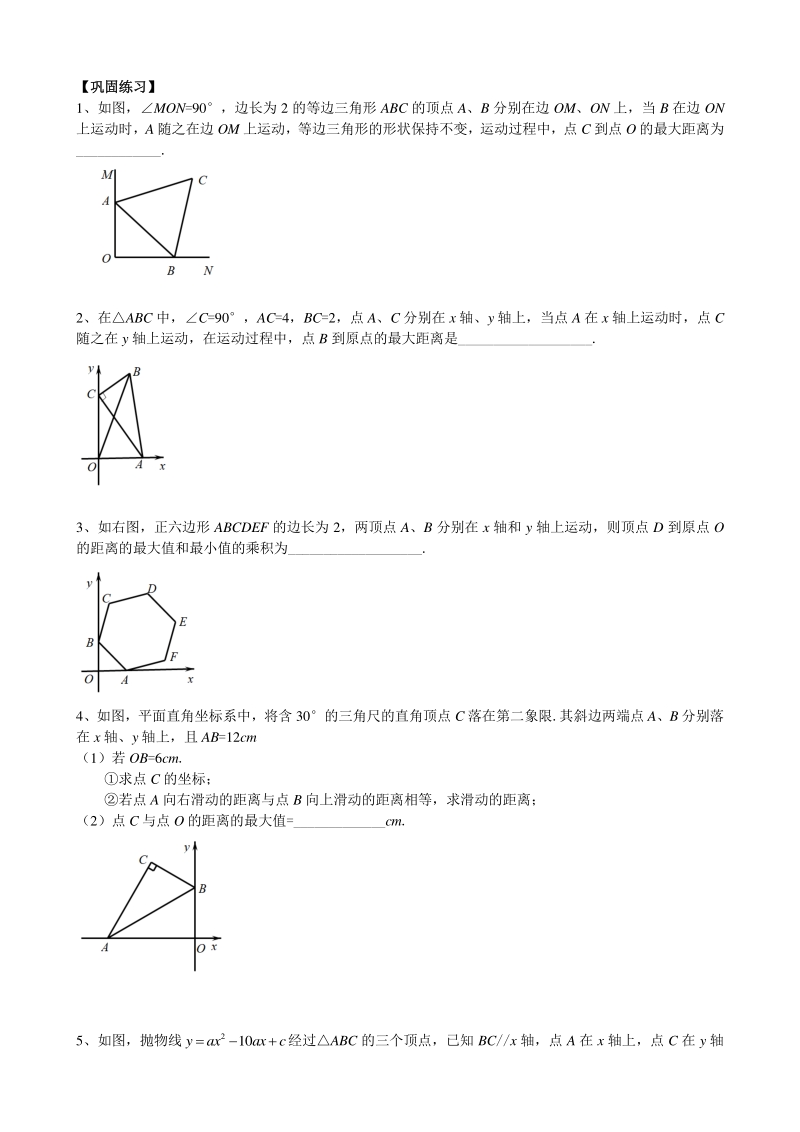
7、完成解题过程） （4）综合应用：）综合应用： 如图 5，E，F 是正方形 ABCD 的边 AD 上两个动点，满足 AE=DF.连接 CF 交 BD 于点 G，连接 BE 交 AG 于点 H. 若正方形的边长为 2，则线段 DH 长度的最小值是_. 如图 6，平面直角坐标系中，分别以点 A（-2，3） ，B（3，4）为圆心，以 1、2 为半径作A、B， M、N 分别是A、B 上的动点，P 为 x 轴上的动点，则 PM+PN 的最小值等于_. 1.解：如图，取 AB 的中点 D，连接 OD、CD， ABC 是等边三角形， CD2， MON90， ODAB21， 由图可知，当点 O、C、D 三点共线

8、时点 C 到点 O 的距离最大， 最大值为+1 故答案为：+1 2.解：如图，取 CA 的中点 D，连接 OD、BD， 则 ODCDAC42， 由勾股定理得，BD2， 当 O、D、B 三点共线时点 B 到原点的距离最大， 所以，点 B 到原点的最大距离是 2+2 故答案为：2+2 3.解：当 O、D、AB 中点共线时，OD 有最大值和最小值， 如图，BD2，BK1， DK，OKBK1， OD 的最大值为：1+， 同理，把图象沿 AB 边翻折 180得最小值为：1+121， 顶点 D 到原点 O 的距离的最大值和最小值的乘积为： （+1） （1）12 故答案为：12 4.解： （1）过点 C 作

9、 y 轴的垂线，垂足为 D，如图 1： 在 RtAOB 中，AB12，OB6，则 BC6， BAO30，ABO60， 又CBA60， CBD60，BCD30， BD3，CD3， 所以点 C 的坐标为（3，9） ； 设点 A 向右滑动的距离为 x，根据题意得点 B 向上滑动的距离也为 x，如图 2： AO12cosBAO12cos306 AO6x，BO6+x，ABAB12 在AO B中，由勾股定理得， （6x）2+（6+x）2122， 解得：x6（1） ， 滑动的距离为 6（1） ； （2）设点 C 的坐标为（x，y） ，过 C 作 CEx 轴，CDy 轴，垂足分别为 E，D，如图 3： 则 O

10、Ex，ODy， ACE+BCE90，DCB+BCE90， ACEDCB， 又AECBDC90， ACEBCD， ，即， yx， OC2x2+y2x2+（x）24x2， 取 AB 中点 D，连接 CD，OD，则 CD 与 OD 之和大于或等于 CO，当且仅当 C，D，O 三点共线时取 等号，此时 COCD+OD6+612， 故答案为：12 5.解： （1）OABC，ACBC 设 OA3k，ACBC5k（k0） OC 当 x0 时，yax210ax+cc C（0，c） ，即 OCc4k k A（，0）B（，c） 抛物线经过点 A、B 解得： 抛物线解析式为：yx2+x+8 （2）如图 2，在 x

11、轴上截取 AEAC，连接 QE ACBC CABCBA CBx 轴 CBABAD CABBAD 在ACQ 与AEQ 中 ACQAEQ（SAS） QCQE |QCQD|QEQD|DE y0 时，x2+x+80，解得：x16，x216 A（6，0） ，D（16，0） AEAC10 DEADAEADAC16（6）1012 0|QCQD|12 1.解：如图 1，取 BC 的中点 E， 连接 AE，交半圆于 P，在半圆上取一点 P，连接 AP，EP， 在AEP 中，AP+EPAE， 即：AP是 AP 的最小值， AE，PE1， AP1； 故答案为：1； 2.解：A（1，0） ，B（1a，0） ，C（1+

12、a，0） （a0） ， AB1（1a）a，CAa+11a， ABAC， BPC90， PAABACa， 如图延长 AD 交D 于 P，此时 AP最大， A（1，0） ，D（4，4） ， AD5， AP5+16， a 的最大值为 6 故答案为 6 3.解：如图，设O 与 AC 相切于点 E，连接 OE，作 OP1BC 垂足为 P1交O 于 Q1， 此时垂线段 OP1最短，P1Q1最小值为 OP1OQ1， AB10，AC8，BC6， AB2AC2+BC2， C90， OP1B90， OP1AC AOOB， P1CP1B， OP1AC4， P1Q1最小值为 OP1OQ11， 如图，当 Q2在 AB

13、边上时，P2 与 B 重合时，P2Q2经过圆心，经过圆心的弦最长， P2Q2最大值5+38， PQ 长的最大值与最小值的和是 9 故答案为：9 4.解：过 C 作 CMAB 于 M，连接 AC，MC 的延长线交C 于 N， 则由三角形面积公式得，ABCMOABC， 5CM16， CM， 圆 C 上点到直线 yx3 的最小距离是 1， PAB 面积的最小值是 5， 故答案是： 5.解：在 RtABC 中，由勾股定理可知：AC4， 由轴对称的性质可知：BCCB3， 当 A、B、C 三点在一条直线上时，BA 有最小值， BAminACBC431 故答案为：1 6.解：如图，连接 MC；过点 M 作

14、MECD， 交 CD 的延长线于点 E； 四边形 ABCD 为平行四边形， ADBC，ADBC4， 点 M 为 AD 的中点，BCD30， DMMA2，MDEBCD30， MEDM1，DE， CECD+DE4，由勾股定理得： CM2ME2+CE2， CM7；由翻折变换的性质得：MAMA2， 显然，当折线 MAC 与线段 MC 重合时， 线段 AC 的长度最短，此时 AC725， 故答案为 5 7.解：作 A 点关于直线 DC 的对称点 A，连接 BD，DA， 可得 AADC，则BAA90，故A30， 则ABA60，ADNADN60， ABAD，BAD60， ABD 是等边三角形， ADB60，

15、 ADB+ADA180， A，D，B 在一条直线上， 由题意可得出：此时 P 与 D 重合，E 点在 AD 上，F 在 BD 上，此时 PE+PF 最小， 菱形 ABCD 中，A60， ABAD，则ABD 是等边三角形， BDABAD3， A、B 的半径分别为 2 和 1， PE1，DF2， PE+PF 的最小值是 3 故答案为：3 8.解：EF2，点 G 为 EF 的中点， DG1， G 是以 D 为圆心，以 1 为半径的圆弧上的点， 作 A 关于 BC 的对称点 A， 连接 AD， 交 BC 于 P， 交以 D 为圆心， 以 1 为半径的圆于 G， 此时 PA+PG 的值最小，最小值为 A

16、G 的长； AB2，AD3， AA4， AD5， AGADDG514； PA+PG 的最小值为 4； 故答案为 4 9.解：CPQ 的周长PQ+QC+CPBQ+QC+CPBC+PC1+PC； 又PCACPA1， CPQ 的周长1+1， 即当点 P 运动至点 P0时，CPQ 的周长最小值是 10.解答： （1）证明：如图 2，在O 上任取一点 C（不为点 A、B） ，连接 PC、OC POPC+OC，POPA+OA，OAOC， PAPC， PA 是点 P 到O 上的点的最短距离； （2）解：连接 AO 与O 相交于点 P，如图 3，由已知定理可知， 此时 AP 最短， ACB90，ACBC2，B

17、C 为直径， POCO1， AO， AP1， 故答案为：1； （3）解：如图 4，由折叠知 AMAM，又 M 是 AD 的中点，可得 MAMAMD， 故点 A在以 AD 为直径的圆上， 由模型可知，当点 A在 BM 上时，AB 长度取得最小值， 边长为 2 的菱形 ABCD 中，A60，M 是 AD 边的中点， BM， 故 AB 的最小值为：1； （4）解：在正方形 ABCD 中，ABADCD，BADCDA，ADGCDG， 在ABE 和DCF 中， ， ABEDCF（SAS） ， 12， 在ADG 和CDG 中， ， ADGCDG（SAS） ， 23， 13， BAH+3BAD90， 1+BAH90， AHB1809090， 取 AB 的中点 O，连接 OH、OD， 则 OHAOAB1， 在 RtAOD 中，OD， 根据三角形的三边关系，OH+DHOD， 当 O、D、H 三点共线时，DH 的长度最小， 最小值ODOH1 故答案为：1； 解：作A 关于 x 轴的对称A，连接 BA分别交A和B 于 M、N，交 x 轴于 P，如图 6， 则此时 PM+PN 最小， 点 A 坐标（2，3） ， 点 A坐标（2，3） ， 点 B（3，4） ， AB， MNABBNAM213， PM+PN 的最小值为3 故答案为：3