中考培优竞赛专题经典讲义 第2讲 垂直平分线

《中考培优竞赛专题经典讲义 第2讲 垂直平分线》由会员分享，可在线阅读，更多相关《中考培优竞赛专题经典讲义 第2讲 垂直平分线（12页珍藏版）》请在七七文库上搜索。

1、第第 2 2 讲讲 垂直平分线垂直平分线 1.垂直平分线性质定理：线段垂直平分线上的点到这条线段两个端点的距离相等. PD 为线段 AB 的垂直平分线，必然需要连接 PA、PB，构造出等腰PAB，进而求解. 逆定理：若 PA=PB，则点 P在 AB的垂直平分线上. 【例题讲解】【例题讲解】 例例题题 1 1、如图，在ABC中，点 D、E、F 分别在 BC、AB、AC 上.BD=CF，BE=CD，DGEF 于点 G，且 EG=FG.求证：AB=AC. 【分析】可知 GD为 EF的垂直平分线，遇见垂直平分线，必然要将垂直平分线上的点与线段两端点连接 【解答】解：连接 DE、DF 如右图所示 ,DG

2、EF EGFG DEDF 在BDE和CFD 中， BDCF BECD DEDF BDECFD BC ABAC. 例题例题 2 2、如图，在 RtABC 中，C=90，点 D 在 BC 上，点 E 在 AB 上，且 DEAC，AE=5，DE=2， DC=3，动点 P 从点 A 出发，沿边 AC以每秒 2 个单位长的速度向终点 C运动，设运动时间为 t秒。 （1）线段 AC 的长= ； （2）在线段 EA上有一点 Q，满足 ED=EQ，连接 DQ、PE，当 PEDQ时，求出 t的值. 【解答】 （1）AC=6； （2）当 PEDQ时，由于 ED=EQ，易证 PE 垂直平分 DQ， 所以连接 PD、

3、PQ，只需使 PD=PQ 即可 可知 AP=2t，所以 PC=6-2t；CD=3，EQ=2，所以 AQ=3， 所以 412 55 AFAQ， 39 55 QFAQ 所以 12 2 5 PFt 在 RtPCD 中，PD 2=32+（6-2t）2； 在 RtPQF 中，PQ 2= 22 129 2 55 t 所以 3 2+（6-2t）2= 22 129 2 55 t ，解得 5 2 t . 【总结】遇见垂直平分线，连接垂直平分线上的点与线段两端点是必然的！ 【最好方法】 当 PEDQ时， 易证 PE平分DEA， 由 【角平分线模型三】 可知， 平行+角平分线=等腰三角形， 所以AEP 为等腰三角形

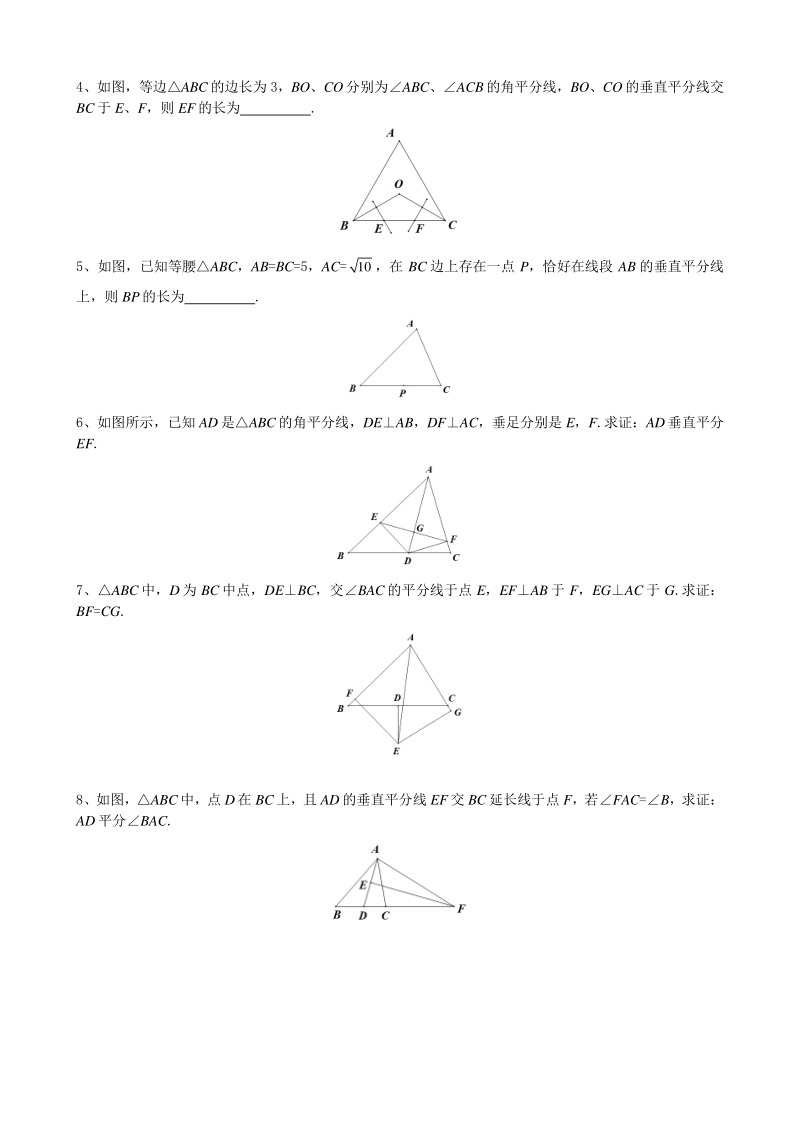
4、，所以 AP=AE=5，即 2t=5，t= 5 2 . 【巩固练习】【巩固练习】 1、三角形三条边的垂直平分线的交点是三角形的（ ） A.重心 B.内心 C.外心 D.中心 2、在AOB的内部有一点 P，点 P与 P1关于 OA对称，点 P与 P2关于 BO对称，则OP1P2是（ ） A.等边三角形 B.等腰三角形 C.直角三角形 D.钝角三角形 当AOB 满足什么条件时，OP1P2是等边三角形？ 3、如图，ABC 中，AB，AC的垂直平分线交 BC于 D、E， （1）若BAC=100，则DAE= ； （2）若BAC=80，则DAE= ； （3）若DAE=10，则BAC= ； （4）若ABC的

5、周长为 20，ADE 的周长为 12，则 AB+AC= ； （5）当 AB=AC，且BAC=120，则ADE为何种特殊三角形？ 4、如图，等边ABC 的边长为 3，BO、CO分别为ABC、ACB的角平分线，BO、CO 的垂直平分线交 BC 于 E、F，则 EF的长为 . 5、如图，已知等腰ABC，AB=BC=5，AC=10，在 BC 边上存在一点 P，恰好在线段 AB 的垂直平分线 上，则 BP的长为 . 6、如图所示，已知 AD 是ABC 的角平分线，DEAB，DFAC，垂足分别是 E，F.求证：AD垂直平分 EF. 7、ABC 中，D 为 BC 中点，DEBC，交BAC 的平分线于点 E，

6、EFAB 于 F，EGAC 于 G.求证： BF=CG. 8、如图，ABC 中，点 D在 BC上，且 AD 的垂直平分线 EF 交 BC 延长线于点 F，若FAC=B，求证： AD 平分BAC. 9、如图，在ABC中，AB=AC，D为三角形内一点，且DBC 为等边三角形. （1）求证：直线 AD垂直平分 BC； （2）以 AB为一边，在 AB 的右侧画等边ABE，连接 DE，试判断以 DA、DB、DE三条线段是否能构成 直角三角形？请说明理由. 10、 已知二次函数 y=ax 2+2ax+c 的图象与 x 轴分别交于 A、 B 两点 （点 A在点 B的左侧） ， 与 y轴交于点 C， 顶点为

7、P，若 C（0，2），BC的垂直平分线过点 A，求这个二次函数的关系式. 11、如图，在平面直角坐标系中，直线 y= 4 3 x+4 与 x 轴交于点 A，与 y 轴交于点 B，点 P 从点 O 出发沿 OA 以每秒 1 个单位长的速度向点 A匀速运动，到达点 A后立刻以原来的速度沿 AO 返回；点 Q从 A出发 沿 AB 以每秒 1 个单位长的速度向点 B 匀速运动，当点 P、Q 运动时，DE 保持垂直平分 PQ，且交 PQ 于 点 D，交折线 QB-BO-OP于点 E.点 P、Q同时出发，当点 Q到达点 B时停止运动，点 P也随之停止，设 点 P、Q 运动的时间为 t秒（t0）. （1）点

8、 Q的坐标是（ ， ）（用含 t的代数式表示）； （2）当 t为何值时，直线 DE 经过点 O. 12、如图 1，在矩形 ABCD中，AB=4，BC=3，点 E是射线 CD上的一个动点，把BCE沿 BE折叠，点 C 的对应点为 F. （1）若点 F刚好落在线段 AD 的垂直平分线上时，求线段 CE 的长； （2）若点 F刚好落在线段 AB的垂直平分线上时，求线段 CE的长； （3）当射线 AF交线段 CD于点 G时，请直接写出 CG 的最大值 . 13、如图，二次函数的图象与 x 轴相交于点 A（-3，0）、B（-1，0），与 y轴相交于点 C（0，3），点 P 是该图象上的动点，点 Q的坐标

9、为（4，0）. （1）求该二次函数的表达式； （2）当 OP/CQ时，求点 P 的坐标； （3）点 M，N分别在线段 AQ、CQ上，点 M 以每秒 3 个单位长度的速度从点 A 向点 Q运动，同时，点 N 以每秒 1 个单位长度的速度从点 C 向点 Q 运动，当点 M，N 中有一点到达 Q点时，两点同时停止运动.设 运动时间为 t秒，当直线 PQ垂直平分线段 MN时，请求出此时 t的值及点 P的坐标. 14、已知抛物线 y=ax 2+bx+c（a0）与 x轴交于点 A（8，0）和 B（一 12，0），与 y轴交于点 C（0，6）. （1）求该抛物线的解析式； （2）点 D在线段 AB 上且 A

10、D=AC，若动点 M 从 A出发沿线段 AB 以每秒 1 个单位长度的速度匀速运动， 同时另一动点 N以某一速度从 B出发沿线段 BC匀速运动，问是否存在某一时刻 t（秒），使线段 MN被直 线 CD垂直平分？若存在，请求出此时的时间 t和点 N 的运动速度；若不存在，请说明理由； 参考答案参考答案 1. 答案：B 2. 答案：B；AOB=30 3. 答案：（1）20；（2）20；（3）95；（4）8；（5）等边三角形. 4. 答案：1 5. 答案： 25 8 6. 证明：AD是ABC的角平分线，DEAB，DFAC，DE=DF 在 RtADE 和 RtADF中，AD=AD，DE=DF， RtA

11、DERADF(HL)， AEAF，又 DEDF， AD 垂直平分 EF(到线段两端点的距离相等的点一定在线段的垂直平分线上) 7. 证明：如图，连接 BE、BC， EDBC，D 为 BC 中点 BE= EC EFAB，EGAG，且 AB 平分FAG FE=EG 在BFE和 RtCGE 中，BE=CE，EF=EG， RtBFERtCGE(HL)， BF=CG. 8. 证明：EF是 AD的垂直平分线， AF=DF EAFEDF， EAFFAC+CAD，EDFBAD+B， 又FACB BADCAD， 即 AD平分BAC. 9. 答案：(1)DBC为等边三角形，DB=DC，D 在 BC的垂直平分线上

12、ABAC，A在 BC的垂直平分线上， 直线 AD 垂直平分 BC； (2)以 DA，DB，DE 三条线段能构成直角三角形； 理由:连接 CE， ABDABE-DBE=60-DBE=DBC-DBE=EBC， 在EBC和ABD中，AB=EB，ABDEBC，DB=CB， EBCABD（SAS）， BCEADB，ADCE. 在ADB和ADC 中，AD=AD，AB=AC，DB=DC， ADBADC（SSS）， ADBADC， ADB 1 2 (360-BCD）150 BCEBDA150， DCEBCE-BCD=150-60=90 CEDA，DCDB， 以 DA，DB，DE三条线段能构成直角三角形. 10

13、. 解：BC 的垂直平分线过点 A，ABAC, 二次函数 y=ax 2+2ax+c 的对称轴为2 1 2 a x a ， 设2ABACm，则1,1AOmBOm， 0,2C，2CO 在 RtAOC 中， 222 AOCOAC,即 22 2 122mm，解得1m 或 5 3 ， 当1m 时，0,0 ,2,0 ,0,2ABC（舍去）； 当 5 3 m 时， 82 ,0 ,0 ,0,2 33 ABC ,此时二次函数解析式为 2 99 2 84 yxx . 11. 答案：（1） 34 3, 55 tt ； （2）四边形 QBED 能成为直角梯形。 当 0t3 时，AQOPt，3APt， 如图 2，当 D

14、EQB时，DEPQ，PQQB，四边形 QBED 是直角梯形. 此时AQP90. 由APQABO得 AQAP AOAB . 3 35 tt .解得 9 8 t ； 如图 3，当 PQBO时，DEPQ，DEBO，四边形 QBED 是直角梯形. 此时APQ90. 由AQPABO，得 AQAP ABAO . 即 3 53 tt ，解得 15 8 t ； 当 3t5 时，AQt，APt-3， 如图 2，当 DBQB时，DEPQ，PQQB，四边形 QBED 是直角梯形。 此时AQP90. 由APQABO，得 AQAP AOAB . 3 35 tt . 解得 9 2 t （舍去）； 如图 3，当 PQBO时

15、，DEPQ，DEBO，四边形 QBED 是直角梯形。 此时APQ90。 由AQPABO，得 AQAP ABAO . 即 3 53 tt .解得 15 5 2 t (舍去)； 综上所述:t 9 8 或15 8 ； (3)当 t 5 2 或 45 14 时，DB 经过点 O. 理由:如图 4，当 DE 经过点 O时， DB 垂直平分 PQ，EP=EQ=t, 由于 P与 Q 运动的时间和速度相同， AQEQEPt， AEQEAQ， AEQ+BEQ90，EAQ+EBQ90, BEQEBQ，BQ=BQ,EQ=AQ=BQ= 1 2 AB， 5 2 t ； 如图 5，当 P从 A 向 O运动时，过点 Q作

16、QFOB于 F， EP6-t，EQEP6-t， AQt, BQ=5-t, 3 sin 5 OA ABO AB ， 4 cos 5 OB ABO AB ， 33 53 55 FQtt， 44 54 55 BFtt， 4 4 5 EFBFt, 222 EFFQEQ，即 22 234 36 55 ttt ， 解得: 45 14 t . 当 DE经过点 O时，t 5 2 或 45 14 . 12. 解：（1）如图，MN 是线段 AD的中垂线，作 FHCD 于 H. 在 RtBFH中，3 BCBF， 2 3 BM， 222 CHBMBF 3 2 3 CHFM， 设xEFCE，在 RtEFH 中，因为 2

17、22 HEFHEF， 2 x 22 )- 2 33 2 3 x（）（， 3x，即3CE. （2）如图，MN 是线段 AB 的中垂线，设 EF=CE=x， 在 RtBFM 中，因为BMF90，BM2，BF=BC=3， 5- 22 BMBFMF， MN=BC=3 FN=5-3，xEN-2， 在 RtEFN中， 222 NEFNEF， 2 2 2 -25-3xx， 2 53-9 x. （3）如图，欲求 CG的最大值，只要求出 DG的最小值即可， DGADtanGAD，所以GAD 最小时，DG的值最小， BFBC，BF 是定值， 当 BFAG时，BAF的值最大，即DAG的值最小， 当 BFAG 时，易

18、知点 B与点 G共点， 设 CGGFx， 在 RtABF中，AFB90，AB4，BF=BC=3. 222 43 AF,即 AF=7. 在 RtABF中， 222 AGDGAD,即 222 )7()-43xx（，7-4x. CG的最大值为 4-7. 13. 解：（1）设抛物线的解析式为:yax 2+bx+c， 抛物线经过点 C(0，3)， C3 把 A(-3，0)、B(-1，0)代入 yax 2+bx+3 中 9a-3b+3=0，a-b+3=0， 解得 a=1，b=4. 抛物线的解析式为:yx 2+4x+3 （2）设 CQ的直线方程为 ykx+b，将 C(0，3)和 Q(4，0)带入解得 CQ的

19、直线方程为y-3 4 3 x， OPCQ， 直线 OP的方程为 y-x 4 3 ， 联立y-3 4 3 x和 y-x 4 3 ，解得 1 x- 4 3 ， 2 x-4， P的坐标为（- 4 3 ， 16 9 ）、（-4，3）； （3）过点作 ND轴于点 D，则 NDOC， 直线 PQ 能够垂直平分线段 MN，则有 QMQN，且 PQMN，PQ平分AQC. 由 QMQN，得:7-3t5-t，解得 t=1. 设 P(x，x 2+4x+3)，若直线 PQMN，则:过 P作直线 PEx 轴，垂足为 E，则PEQMDN， ND MD EQ PE , 5 12 5 4 -4 34 2 x xx , 6 1

20、0913- x, P( 18 10937 , 6 109-13- )或（ 18 109-37 , 6 10913- ）. 14. 解：（1）抛物线 yax 2+bx+c(a0)与 x轴交于点 A(8，0)和 B(-12，0)， 可设抛物线的解析式为 y=a(x-8)(x+12), 又抛物线过点 C(0，6)，6-96a，解得 a- 16 1 ， 抛物线的解析式为 y=- 16 1 (x-8)(x+12)=- 2 16 1 x - 6 4 1 x ， 即该抛物线的解析式为 y=- 2 16 1 x - 6 4 1 x . （2）A(8,0),C(0,6),AC=1068 22 , AD=AC=1

21、0，点 D 的坐标是(-2，0) B(-12,0),BD= AD. 若 CD垂直平分 MN，则 DNDM，NDCMDCACD， DNAC， BN=CN DN是ABC的中位线，DN=5 2 AC , AM=t=5, 而 BN5VN53，点 N 的运动速度是 5 53 ； （3）SPCASPCB， A、B到 PC 的距离相等， PCAB P、C 关于抛物线 y- 2 16 1 x - 6 4 1 x的对称轴 x-2 对称， C(0,6), P(-4,6) tanPBQ 2 1 ，tanCBA 2 1 12 6 OB OC ， PBQCBA， PBQ-CBQCBA-CBQ，即PBQCBQ 作 PGBC于 G，QHAB于 H. 5 54 56 64 BC OCPC PG , 5 58 ) 5 54 (-4- 2222 PGPCCG ， 5 522 5 58 -56-CGBCBG ， tanPBC 11 2 5 522 5 54 BG PG . 设点 Q的坐标为(x，- 2 16 1 x - 6 4 1 x ） tanQBAtanPBC， 11 2 12 6 4 1 - 16 1 - 2 x xx , 解得 11 56 x 或-12（舍去） 故点 Q的坐标是( 121 376 11 56， ）.