备战2020高考物理专题14《机械振动与机械波光电磁波与相对论》

《备战2020高考物理专题14《机械振动与机械波光电磁波与相对论》》由会员分享，可在线阅读，更多相关《备战2020高考物理专题14《机械振动与机械波光电磁波与相对论》（20页珍藏版）》请在七七文库上搜索。

1、 1 / 20 备战 2020 高考物理最全知识点分专题归纳总结（选修 3-4） 专题 14机械振动与机械波 光 电磁波与相对论 第一节第一节 机械振动机械振动( (实验： 探究单摆的运动、 用单摆测定重力加速度实验： 探究单摆的运动、 用单摆测定重力加速度) ) 【基本概念、规律】【基本概念、规律】 一、简谐运动 1概念：质点的位移与时间的关系遵从正弦函数的规律，即它的振动图象(xt 图象) 是一条正弦曲线的振动 2平衡位置：物体在振动过程中回复力为零的位置 3回复力 (1)定义：使物体返回到平衡位置的力 (2)方向：时刻指向平衡位置 (3)来源：振动物体所受的沿振动方向的合力 4简谐运动的

2、表达式 (1)动力学表达式：Fkx，其中“”表示回复力与位移的方向相反 (2)运动学表达式： xAsin (t)， 其中 A 代表振幅， 2f 表示简谐运动的快慢， (t )代表简谐运动的相位， 叫做初相 5描述简谐运动的物理量 定义 意义 振幅 振动质点离开平衡位置的最大距离 描述振动的强弱和能量 周期 振动物体完成一次全振动所需时间 描述振动的快慢，两者互为倒数：T1 f 频率 振动物体单位时间内完成全振动的 次数 相位 t 描述质点在各个时刻所处的不同状态 二、单摆 1定义：在细线的一端拴一个小球，另一端固定在悬点上，如果细线的伸缩和质量都 不计，球的直径比线的长度短得多，这样的装置叫做

3、单摆 2视为简谐运动的条件：5 . 3回复力：FG2Gsin mg l x. 4周期公式：T2 l g. 5单摆的等时性：单摆的振动周期取决于摆长 l 和重力加速度 g，与振幅和振子(小球) 2 / 20 质量都没有关系 三、受迫振动及共振 1受迫振动：系统在驱动力作用下的振动做受迫振动的物体，它的周期(或频率)等 于驱动力周期(或频率)，而与物体的固有周期(或频率)无关 2共振：做受迫振动的物体，它的固有频率与驱动力的频率越接近，其振幅就越大， 当二者相等时，振幅达到最大，这就是共振现象共振曲线如图所示 【重要考点归纳】【重要考点归纳】 考点一考点一 简谐运动的五个特征简谐运动的五个特征 1

4、动力学特征 Fkx，“”表示回复力的方向与位移方向相反，k 是比例系数，不一定是弹簧的劲 度系数 2运动学特征 简谐运动的加速度与物体偏离平衡位置的位移成正比而方向相反， 为变加速运动， 远离 平衡位置时 x、F、a、Ep均增大，v、Ek均减小，靠近平衡位置时则相反 3运动的周期性特征 相隔 T 或 nT 的两个时刻振子处于同一位置且振动状态相同 4对称性特征 (1)相隔T 2或 2n1 2 T(n 为正整数)的两个时刻，振子位置关于平衡位置对称，位移、 速度、加速度大小相等，方向相反 (2)如图所示， 振子经过关于平衡位置 O 对称的两点 P、 P(OPOP) 时，速度的大小、动能、势能相等

5、，相对于平衡位置的位移大小相等 (3)振子由 P 到 O 所用时间等于由 O 到 P所用时间，即 tPOtOP. (4)振子往复过程中通过同一段路程(如 OP 段)所用时间相等，即 tOPtPO. 5能量特征 振动的能量包括动能 Ek和势能 Ep，简谐运动过程中，系统动能与势能相互转化，系统 的机械能守恒 3 / 20 6.(1)由于简谐运动具有周期性、 往复性、 对称性， 因此涉及简谐运动时， 往往出现多解 分 析此类问题时，特别应注意，物体在某一位置时，位移是确定的，而速度不确定，时间也存 在周期性关系 (2)相隔(2n1)T 2的两个时刻振子的位置关于平衡位置对称，位移、速度、加速度等大

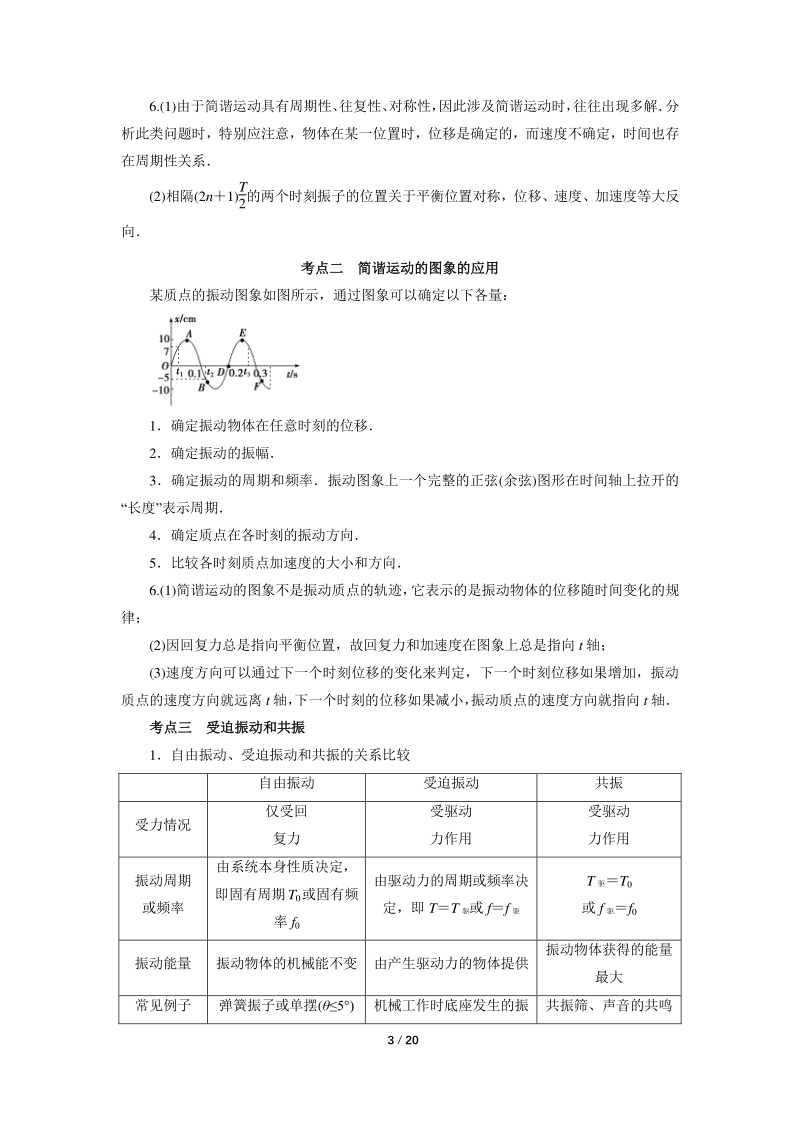
6、反 向 考点二考点二 简谐运动的图象的应用简谐运动的图象的应用 某质点的振动图象如图所示，通过图象可以确定以下各量： 1确定振动物体在任意时刻的位移 2确定振动的振幅 3确定振动的周期和频率振动图象上一个完整的正弦(余弦)图形在时间轴上拉开的 “长度”表示周期 4确定质点在各时刻的振动方向 5比较各时刻质点加速度的大小和方向 6.(1)简谐运动的图象不是振动质点的轨迹， 它表示的是振动物体的位移随时间变化的规 律； (2)因回复力总是指向平衡位置，故回复力和加速度在图象上总是指向 t 轴； (3)速度方向可以通过下一个时刻位移的变化来判定，下一个时刻位移如果增加，振动 质点的速度方向就远离 t

7、 轴， 下一个时刻的位移如果减小， 振动质点的速度方向就指向 t 轴 考点三考点三 受迫振动和共振受迫振动和共振 1自由振动、受迫振动和共振的关系比较 自由振动 受迫振动 共振 受力情况 仅受回 复力 受驱动 力作用 受驱动 力作用 振动周期 或频率 由系统本身性质决定， 即固有周期T0或固有频 率 f0 由驱动力的周期或频率决 定，即 TT驱或 ff驱 T驱T0 或 f驱f0 振动能量 振动物体的机械能不变 由产生驱动力的物体提供 振动物体获得的能量 最大 常见例子 弹簧振子或单摆(5) 机械工作时底座发生的振共振筛、声音的共鸣 4 / 20 动 等 2.对共振的理解 (1)共振曲线：如图所

8、示，横坐标为驱动力频率 f，纵坐标为振幅 A.它直观地反映了驱动 力频率对某振动系统受迫振动振幅的影响，由图可知，f 与 f0越接近，振幅 A 越大；当 ff0 时，振幅 A 最大 (2)受迫振动中系统能量的转化：受迫振动系统机械能不守恒，系统与外界时刻进行能 量交换 3.(1)无论发生共振与否，受迫振动的频率都等于驱动力的频率，但只有发生共振现象时 振幅才能达到最大. (2)受迫振动系统中的能量转化不再只有系统内部动能和势能的转化，还有驱动力对系 统做正功补偿系统因克服阻力而损失的机械能 考点四考点四 实验：用单摆测定重力加速度实验：用单摆测定重力加速度 1实验原理 由单摆的周期公式 T2

9、l g，可得出 g 42 T2 l，测出单摆的摆长 l 和振动周期 T，就可 求出当地的重力加速度 g. 2实验器材 单摆、游标卡尺、毫米刻度尺、停表 3实验步骤 (1)做单摆： 取约 1 m 长的细丝线穿过带中心孔的小钢球， 并打一个比小孔大一些的结， 然后把线的另一端用铁夹固定在铁架台上，让摆球自然下垂，如图所示 (2)测摆长：用毫米刻度尺量出摆线长 L(精确到毫米)，用游标卡尺测出小球直径 D，则 单摆的摆长 lLD 2. (3)测周期：将单摆从平衡位置拉开一个角度(小于 5 )，然后释放小球，记下单摆摆动 3050 次的总时间，算出平均每摆动一次的时间，即为单摆的振动周期 5 / 20

10、 (4)改变摆长，重做几次实验 4数据处理 (1)公式法：g4 2l T2 . (2)图象法：画 lT2图象 g42k，k l T2 l T2. 5注意事项 (1)悬线顶端不能晃动，需用夹子夹住，保证悬点固定 (2)单摆必须在同一平面内振动，且摆角小于 10 . (3)选择在摆球摆到平衡位置处时开始计时，并数准全振动的次数 (4)小球自然下垂时，用毫米刻度尺量出悬线长 L，用游标卡尺测量小球的直径，然后算 出摆球的半径 r，则摆长 lLr. (5)选用一米左右的细线 【思想方法与技巧】【思想方法与技巧】 单摆模型的应用单摆模型的应用 (1)单摆模型指符合单摆规律的模型，须满足以下三个条件：圆弧

11、运动；小角度往 复运动；回复力满足 Fkx. (2)处理方法：首先确认符合单摆模型的条件，即小球沿光滑圆弧运动，小球受重力、 轨道支持力，此支持力类似单摆中的摆线拉力，此装置可称为“类单摆”；然后寻找等效摆长 l 及等效加速度 g；最后利用公式 T2 l g或简谐运动规律分析求解问题 (3)须注意单摆模型做简谐运动时具有往复性，解题时要审清题意，防止漏解或多解 第二节第二节 机械波机械波 【基本概念、规律】【基本概念、规律】 一、机械波 1形成条件 (1)有发生机械振动的波源 (2)有传播介质，如空气、水等 2传播特点 6 / 20 (1)传播振动形式、传递能量、传递信息 (2)质点不随波迁移

12、 3分类 机械波 横波：振动方向与传播方向垂直. 纵波：振动方向与传播方向在同一直线上. 二、描述机械波的物理量 1波长 ：在波动中振动相位总是相同的两个相邻质点间的距离用“”表示 2频率 f：在波动中，介质中各质点的振动频率都是相同的，都等于波源的振动频率 3波速 v、波长 和频率 f、周期 T 的关系 公式：v Tf 机械波的速度大小由介质决定，与机械波的频率无关 三、机械波的图象 1图象：在平面直角坐标系中，用横坐标表示介质中各质点的平衡位置，用纵坐标表 示某一时刻各质点偏离平衡位置的位移， 连接各位移矢量的末端， 得出的曲线即为波的图象， 简谐波的图象是正弦(或余弦)曲线 2物理意义：

13、某一时刻介质中各质点相对平衡位置的位移 四、波的衍射和干涉 1波的衍射定义：波可以绕过障碍物继续传播的现象 2发生明显衍射的条件：只有缝、孔的宽度或障碍物的尺寸跟波长相差不多，或者小 于波长时，才会发生明显的衍射现象 3波的叠加原理：几列波相遇时能保持各自的运动状态，继续传播，在它们重叠的区 域里， 介质的质点同时参与这几列波引起的振动， 质点的位移等于这几列波单独传播时引起 的位移的矢量和 4波的干涉 (1)定义：频率相同的两列波叠加时，某些区域的振动加强、某些区域的振动减弱，这 种现象叫波的干涉 (2)条件：两列波的频率相同 5干涉和衍射是波特有的现象，波同时还可以发生反射、折射 五、多普

14、勒效应 由于波源与观察者互相靠近或者互相远离时， 接收到的波的频率与波源频率不相等的现 象 7 / 20 【重要考点归纳】【重要考点归纳】 考点一考点一 波动图象与波速公式的应用波动图象与波速公式的应用 1波的图象反映了在某时刻介质中的质点离开平衡位置的位移情况，图象的横轴表示 各质点的平衡位置，纵轴表示该时刻各质点的位移，如图 图象的应用：(1)直接读取振幅 A 和波长 ，以及该时刻各质点的位移 (2)确定某时刻各质点加速度的方向，并能比较其大小 (3)结合波的传播方向可确定各质点的振动方向或由各质点的振动方向确定波的传播方 向 2波速与波长、周期、频率的关系为：v Tf. 3.波的传播方向

15、与质点的振动方向的互判方法 内容 图象 上下 坡法 沿波的传播方向，上坡时质点向下振动，下 坡时质点向上振动 同侧法 波形图上某点表示传播方向和振动方向的箭 头在图线同侧 微平 移法 将波形图沿传播方向进行微小平移，再由 x 轴上某一位置的两波形曲线上的点来判定 考点二考点二 振动图象与波动图象的综合应用振动图象与波动图象的综合应用 振动图象 波动图象 研究对象 一振动质点 沿波传播方向的所有质点 研究内容 一质点的位移随时间的变化规 律 某时刻所有质点的空间分布规律 图象 物理意义 表示同一质点在各时刻的位移 表示某时刻各质点的位移 8 / 20 图象信息 (1)质点振动周期 (2)质点振幅

16、 (3)某一质点在各时刻的位移 (4)各时刻速度、加速度的方向 (1)波长、振幅 (2)任意一质点在该时刻的位移 (3)任意一质点在该时刻的加速度 方向 (4)传播方向、振动方向的互判 图象变化 随时间推移，图象延续，但已 有形状不变 随时间推移，波形沿传播方向平 移 一完整曲 线占横坐 标的距离 表示一个周期 表示一个波长 1.解决振动图象与波动图象的综合问题的注意点 (1)分清振动图象与波动图象 (2)找准波动图象对应的时刻 (3)找准振动图象描述的质点 考点三考点三 波的干涉、衍射、多普勒效应波的干涉、衍射、多普勒效应 1波的干涉中振动加强点和减弱点的判断 某质点的振动是加强还是减弱，取

17、决于该点到两相干波源的距离之差 r. (1)当两波源振动步调一致时 若 rn(n0,1,2，)，则振动加强； 若 r(2n1) 2(n0,1,2，)，则振动减弱 (2)当两波源振动步调相反时 若 r(2n1) 2(n0,1,2，)，则振动加强； 若 rn(n0,1,2，)，则振动减弱 2 波的衍射现象是指波能绕过障碍物继续传播的现象， 产生明显衍射现象的条件是缝、 孔的宽度或障碍物的尺寸跟波长相差不大或者小于波长 3多普勒效应的成因分析 (1)接收频率： 观察者接收到的频率等于观察者在单位时间内接收到的完全波的个数 当 波以速度 v 通过观察者时，时间 t 内通过的完全波的个数为 Nvt ，因

18、而单位时间内通过观 察者的完全波的个数，即接收频率 (2)当波源与观察者相互靠近时，观察者接收到的频率变大，当波源与观察者相互远离 时，观察者接收到的频率变小 9 / 20 【思想方法与技巧】【思想方法与技巧】 波的多解问题波的多解问题的处理方法的处理方法 1造成波动问题多解的主要因素有 (1)周期性 时间周期性：时间间隔 t 与周期 T 的关系不明确； 空间周期性：波传播距离 x 与波长 的关系不明确 (2)双向性 传播方向双向性：波的传播方向不确定； 振动方向双向性：质点振动方向不确定 2解决波的多解问题的思路 (1)首先要考虑波传播的“双向性”， 例如， nT1 4T 时刻向右传播的波形

19、和 nT 3 4T 时刻向 左传播的波形相同 (2)其次要考虑波的周期性， 若已知一段时间， 就要找出与周期的关系， 写成 tnTt， t1019 10 11 贯穿本领 最强 工业探伤、 医用治疗 特别提醒：(1)波长不同的电磁波，表现出不同的特性，其中波长较长的无线电波和 红外线等，易发生干涉、衍射现象；波长较短的紫外线、X 射线、 射线等，穿透能力较强 (2)电磁波谱中， 相邻两波段的电磁波的波长并没有很明显的界线， 如紫外线和 X 射线、 19 / 20 X 射线和 射线都有重叠，但它们产生的机理不同 考点三考点三 狭义相对论的简单应用狭义相对论的简单应用 1速度变换公式：u uv 1u

20、v c2 . 若 uvc 时，uc，从而证明了光速是速度的极限，也反证了光速不变原理 2相对论质量：m m0 1 v c 2. 从上式可以看出，当物体(一般是粒子)的速度很大时，其运动时的质量明显大于静止时 的质量 3质能方程：Emc2. 含义：反映物体质量和能量之间的关系 由此会有两种能量表达：静止时的能量和运动时的能量；两能量之差就是物体的动能 Ek，即 EkEE0. 4时间间隔的相对性：t 1 v c 2. 含义：运动的时钟变慢，一切物理、生理过程变慢 5长度的相对性：ll01 v c 2. 含义：在运动方向上的长度变小，在垂直运动方向上的长度不变 6.狭义相对论问题的求解技巧 (1)解决“同时”的相对性问题，可从三个方面入手： 令观察者静止，判断被观察者因相对运动而引起的位置变化 结合光速不变原理，分析光传播到两个事件所用的时间 光先传播到的事件先发生，光后传播到的事件后发生 (2)“动尺缩短”是沿运动方向上的长度比其相对静止时测量的长度要短一些，在垂直于 运动方向上的长度没有变化 (3)“动钟变慢”是两个不同惯性系进行时间比较的结果，也是相对的，即两个惯性系中 的观察者都发现对方的钟变慢了 20 / 20