安徽省淮南市2020届高三第二次模拟考试数学试题（理科）含答案解析

上传人：星星

文档编号：140445

上传时间：2020-05-28

格式：DOC

页数：31

大小：422.42KB

《安徽省淮南市2020届高三第二次模拟考试数学试题（理科）含答案解析》由会员分享，可在线阅读，更多相关《安徽省淮南市2020届高三第二次模拟考试数学试题（理科）含答案解析（31页珍藏版）》请在七七文库上搜索。

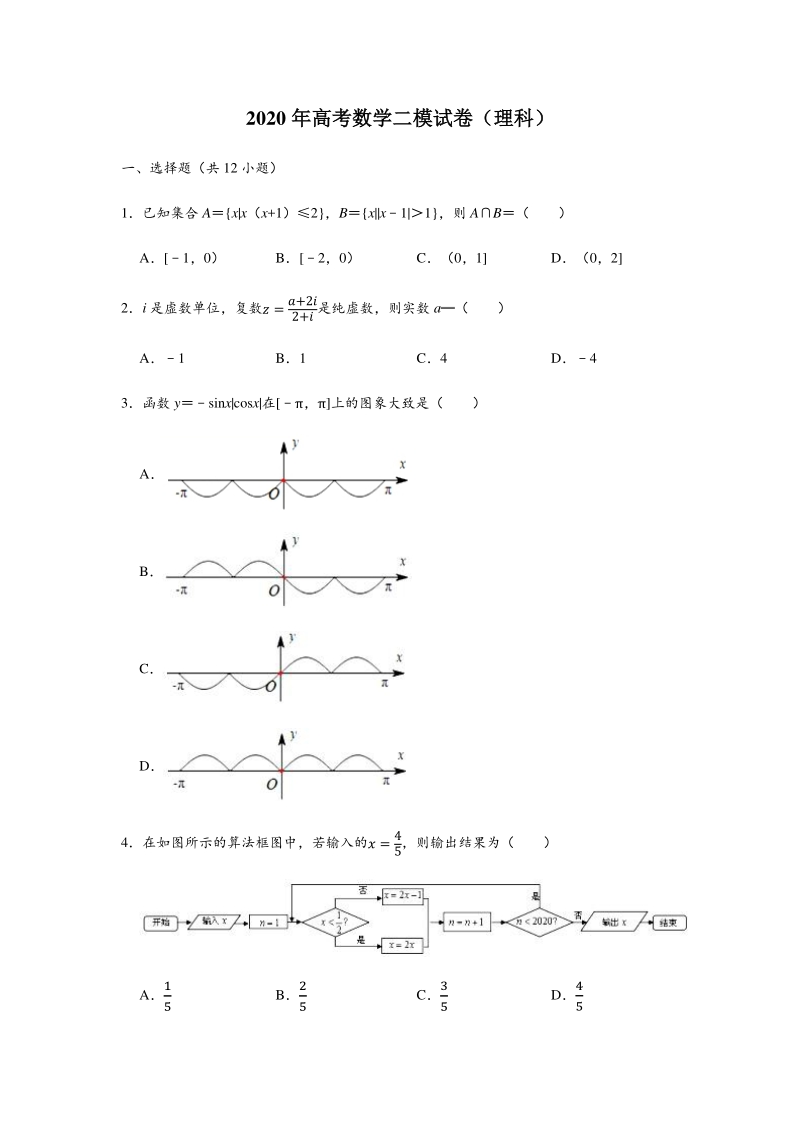
1、2020 年高考数学二模试卷（理科）年高考数学二模试卷（理科）一、选择题（共 12 小题） 1已知集合 Ax|x（x+1）2，Bx|x1|1，则 AB（） A1，0） B2，0） C（0，1 D（0，2 2i 是虚数单位，复数是纯虚数，则实数 a（） A1 B1 C4 D4 3函数 ysinx|cosx|在，上的图象大致是（） A B C D 4在如图所示的算法框图中，若输入的，则输出结果为（） A B C D 5设公差不为 0 的等差数列an的前 n 项和为 Sn若 S17S18，则在 a18，S35，a17a19，S19 S16这四个值中，恒等于 0 的个数是（） A1 B

2、2 C3 D4 6为了得到正弦函数 ysinx 的图象，可将函数的图象向右平移 m 个单位长度，或向左平移 n 个单位长度（m0，n0），则|mn|的最小值是（） A B C D 7如图，网格纸上的小正方形的边长均为 1，粗线画的是一个几何体的三视图，则该几何体的体积是（） A B2 C3 D 8设，，，则（） Aabc Bcba Cbac Dcab 9有四位同学参加校园文化活动，活动共有四个项目，每人限报其中一项已知甲同学报的项目其他同学不报，则 4 位同学所报选项各不相同的概率等于（） A B C D 10在平行四边形 ABCD 中，AB2AD ，E 是 BC 的中点

3、，F 点在边 CD 上，且 CF 2FD，若，则DAB（） A30 B60 C120 D150 11双曲线 C：的右支上一点 P 在第一象限，F1，F2分别为双曲线 C 的左、右焦点，I 为PF1F2的内心，若内切圆 I 的半径为 1，直线 IF1，IF2的斜率分别为 k1，k2，则 k1+k2的值等于（） A B C D 12 定义在 R 上函数 f （x）满足，且当 x0，1）时，f （x）1|2x1|则使得在m，+）上恒成立的 m 的最小值是（） A B C D 二、填空题（本大题共 4 小题，每小题 5 分，共 20 分，将每题的正确答案填在题中的横线上） 13

4、已知公比不为 1 的等比数列an，且 a32a7 ， a 6+2a43a5，则数列的通项公式 an 14在（a+x）（1+x）5展开式中，x 的偶数次幂项的系数之和为 8，则 a 15过抛物线 y24x 焦点 F 的直线交抛物线于点 A、B，交准线于点 P，交 y 轴于点 Q，若，则弦长|AB| 16九章算术卷第五商功中描述几何体“阳马”为“底面为矩形，一棱垂直于底面的四棱锥”现有阳马 SABCD，SA平面 ABCD，AB1，AD3，SA ，BC 上有一点 E，使截面 SDE 的周长最短，则 SE 与 CD 所成角的余弦值等于三、解答题：（本大题满分 60 分.解答应写出文字说明

5、、证明过程或演算步骤.） 17 在ABC中，三内角A， B， C对应的边分别为a， b， c，若B为锐角，且sinA+2sinB cos A （）求 C；（）已知 a2，，求ABC 的面积 18如图，在三棱柱 ABCA1B1C1中，ACBC1CB90，A1AC60，D，E 分别为 A1A 和 B1C1的中点，且 AA1ACBC （）求证：A1E平面 BC1D；（）求平面 BC1D 与平面 ABC 所成锐二面角的余弦值 19已知椭圆 C：的离心率是，原点到直线的距离等于，又知点 Q（0，3）（）求椭圆 C 的标准方程；（）若椭圆 C 上总存在两个点 A、B 关于直线 y

6、x+m 对称，且 3 28，求实数 m 的取值范围 20为了提高生产线的运行效率，工厂对生产线的设备进行了技术改造为了对比技术改造后的效果，采集了生产线的技术改造前后各 20 次连续正常运行的时间长度（单位：天）数据，并绘制了如茎叶图：（）（1）设所采集的 40 个连续正常运行时间的中位数 m，并将连续正常运行时间超过 m 和不超过 m 的次数填入下面的列联表：超过 m 不超过 m 改造前 a b 改造后 c d （2）根据（1）中的列联表，能否有 99%的把握认为生产线技术改造前后的连续正常运行时间有差异？附：K2 ， P（K2k） 0.050 0.010 0.001 k 3

7、.841 6.635 10.828 （）工厂的生产线的运行需要进行维护，工厂对生产线的生产维护费用包括正常维护费、保障维护费两种对生产线设定维护周期为 T 天（即从开工运行到第 kT 天（kN*）进行维护生产线在一个生产周期内设置几个维护周期，每个维护周期相互独立在一个维护周期内，若生产线能连续运行，则不会产生保障维护费；若生产线不能连续运行，则产生保障维护费经测算，正常维护费为 0.5 万元/次；保障维护费第一次为 0.2 万元/ 周期，此后每增加一次则保障维护费增加 0.2 万元现制定生产线一个生产周期（以 120 天计）内的维护方案：T30，k1，2，3，4 以生产线在技术

8、改造后一个维护周期内能连续正常运行的频率作为概率，求一个生产周期内生产维护费的分布列及期望值 21已知函数，（）若 f（x）为 R 上的增函数，求 a 的取值范围；（）若 a0，x1x2，且 f（x1）+f（x2）4，证明：f（x1+x2）2 请考生在第 22、23 题中任选一题作答，如果多做，则按所做的第一题记分作答时请写清题号选修 4-4：坐标系与参数方程 22在平面直角坐标系 xOy 中，曲线 C1的参数方程为（其中为参数），以原点 O 为极点，以 x 轴非负半轴为极轴建立极坐标系，曲线 C2的极坐标方程为 +4cos 0 （）求曲线 C1的普通方程与曲线 C2的直角

9、坐标方程；（）设点 A，B 分别是曲线 C1，C2上两动点且AOB ，求AOB 面积的最大值选修 4-5：不等式选讲 23已知函数 f（x）|xm|+|x |（其中实数 m0）（）当 m1，解不等式 f（x）3；（）求证：f（x） 2 参考答案一、选择题（本大题共 12 小题，每小题 5 分，共 60 分.在每小题给出的四个选项中，只有一项是符合题目要求的，请把正确答案的代号填在题后的括号内） 1已知集合 Ax|x（x+1）2，Bx|x1|1，则 AB（） A1，0） B2，0） C（0，1 D（0，2 【分析】求出集合 A，B，由此能求出 AB 解：Ax|x（x+1）2x|2x

11、cosx|0，排除选项 C 解：函数 ysinx|cosx|在，上是奇函数，其图象关于原点对称，所以排除选项 A，D；当 0x 时，sinx0，所以 ysinx|cosx|0，排除选项 C 故选：B 【点评】本题主要考查了三角函数的图象与性质的应用问题，是基础题 4在如图所示的算法框图中，若输入的，则输出结果为（） A B C D 【分析】模拟程序的运行过程，得出 x 的值呈现以 4 为周期的特点，由此求得 n2020 时输出结果解：模拟程序的运行过程，如下； x ，n1； x ，n2； x ，n3； x ，n4； x ，n5；所以 x 的值呈现以 4 为周期的特点，当 n202

12、0 时，输出结果与 n4 时结果相同，为故选：B 【点评】本题考查了程序框图的运行问题，模拟程序的运行过程是解题的常用方法 5设公差不为 0 的等差数列an的前 n 项和为 Sn若 S17S18，则在 a18，S35，a17a19，S19 S16这四个值中，恒等于 0 的个数是（） A1 B2 C3 D4 【分析】设an的首项为 a1，公差为 d，由 S17S18，即，得 a117d，可得：an，Sn，即可判断出结论解：设an的首项为 a1，公差为 d，由 S17S18，即，得 a117d， an（n18）d， Sn d，所以 a180，S350 a17a19dd2d

13、， S19S16 d d0 故选：C 【点评】本题考查了等差数列的通项公式与求和公式、方程的解法，考查了推理能力与计算能力，属于中档题 6为了得到正弦函数 ysinx 的图象，可将函数的图象向右平移 m 个单位长度，或向左平移 n 个单位长度（m0，n0），则|mn|的最小值是（） A B C D 【分析】直接利用三角函数的图象的平移变换的应用求出结果解：将函数的图象向右平移个单位长度，得到 ysinx 的图象，即 m ，将函数的图象向左平移 2 个单位长度，得到 ysinx 的图象，即 n2，所以|mn|的最小值为故选：B 【点评】本题考查的知识要点：三角函数关系

14、式的恒等变换，函数的关系式的平移变换的应用，主要考查学生的运算能力和转换能力及思维能力，属于基础题型 7如图，网格纸上的小正方形的边长均为 1，粗线画的是一个几何体的三视图，则该几何体的体积是（） A B2 C3 D 【分析】首先把三视图转换为直观图，进一步求出几何体的体积解：根据几何体的三视图转换为直观图为：该几何体为四棱锥体如图所示：所以：V 故选：C 【点评】本题考查的知识要点：三视图和直观图形之间的转换，几何体的体积公式的应用，主要考查学生的运算能力和转换能力及思维能力，属于基础题型 8设，，，则（） Aabc Bcba Cbac Dcab 【分析】利用换底公式可

15、得出，，，容易得出 0log32log34log35，从而可得出 a， b，c 的大小关系解：，，； 0log32log34log35；； abc 故选：A 【点评】考查对数的运算性质，以及对数的换底公式，对数函数的单调性 9有四位同学参加校园文化活动，活动共有四个项目，每人限报其中一项已知甲同学报的项目其他同学不报，则 4 位同学所报选项各不相同的概率等于（） A B C D 【分析】基本事件总数 n 108，4 位同学所报选项各不相同包含的基本事件个数 m 24，由此能求出 4 位同学所报选项各不相同的概率解：有四位同学参加校园文化活动，活动共有四个项目，每人限

16、报其中一项基本事件总数 n 108， 4 位同学所报选项各不相同包含的基本事件个数 m 24， 4 位同学所报选项各不相同的概率 P 故选：C 【点评】本题考查概率的求法，考查古典概型、排列组合等基础知识，考查运算求解能力，是基础题 10在平行四边形 ABCD 中，AB2AD ，E 是 BC 的中点，F 点在边 CD 上，且 CF 2FD，若，则DAB（） A30 B60 C120 D150 【分析】根据所给的图形，把已知向量用矩形的边所在的向量来表示，做出要用的向量的模长，表示出要求得向量的数量积，代入相关数据即可解：如图，结合条件可得，，则（）（） 2 2 2 2

17、，又因为 AB2AD ，即有 AD ，所以 2 cosDAB （2 ） 2 （） 2 ，解得 cosDAB ，所以DAB120，故选：C 【点评】本题考查平面向量的数量积的运算，两个向量的加减法的法则，以及其几何意义，解题的关键是把要用的向量表示成已知向量的和的形式，属于中档题目 11双曲线 C：的右支上一点 P 在第一象限，F1，F2分别为双曲线 C 的左、右焦点，I 为PF1F2的内心，若内切圆 I 的半径为 1，直线 IF1，IF2的斜率分别为 k1，k2，则 k1+k2的值等于（） A B C D 【分析】首先推出 I 的横坐标为 a，由双曲线的方程可得 a，

18、 b， c，求得内心 I 的坐标（3， 1），再由直线的斜率公式，计算可得所求值解：如图所示：可设 F1（c，0）、F2（c，0），设内切圆与 x 轴的切点是点 H， PF1、PF2分别与内切圆的切点分别为 M、N，由双曲线的定义可得|PF1|PF2|2a，由圆的切线长定理知，|PM|PN|，故|MF1|NF2|2a，即|HF1|HF2|2a，设内切圆的圆心横坐标为 x，则点 H 的横坐标为 x，故（x+c）（cx）2a，解得 xa 由双曲线 C：的 a3，b4，c5，由题意可得 I 的纵坐标为 1，即 I（3，1），又 F1（5，0），F2（5，0），可得 k

19、1+k2 ，故选：B 【点评】本题考查双曲线的定义和方程、性质，考查三角形的内切圆的性质，同时考查直线的斜率公式的运用，属于中档题 12 定义在 R 上函数 f （x）满足，且当 x0，1）时，f （x）1|2x1|则使得在m，+）上恒成立的 m 的最小值是（） A B C D 【分析】根据条件一步步转化到 x+33，4）时，x+22，3），f（x+3） f（x+2） | x |0，，画出图象，即可求解结论解：解：x0，1）时，f（x）1|2x1|0，1； x+11，2）时，x0，1），f（x+1） f（x） |x |0，， x+22，3）时，x+11，2），f（x+2）

20、f（x+1） | x |0，， x+33，4）时，x+22，3），f（x+3） f（x+2） | x |0，，令 f（x+3） | x | x 或者 x ；故 x+3 或 x+3 ，所以 m 的最小值为 m ，故选：D 【点评】本题主要考查抽象函数解析式的求解，分段函数，数形结合思想，属于中档题目二、填空题（本大题共 4 小题，每小题 5 分，共 20 分，将每题的正确答案填在题中的横线上） 13 已知公比不为 1的等比数列an，且 a32a7 ， a 6+2a43a5，则数列的通项公式an 2 n+1 【分析】利用等比数列通面公式列出方程组，求出 a14，q2，由此能求

21、出数列的通项公式解：公比不为 1 的等比数列an，且 a32a7，a6+2a43a5，，解得 a14，q2，数列的通项公式 an42n12n+1 故答案为：2n+1 【点评】本题考查数列的通项公式的求法，考查等差数列、等比数列的性质等基础知识，考查运算求解能力，是基础题 14在（a+x）（1+x）5展开式中，x 的偶数次幂项的系数之和为 8，则 a 【分析】给展开式中的 x 分别赋值 1，1，可得两个等式，两式相加，再除以 2 得到答案解：设（a+x）（1+x）5a0+a1x+a2x2+a5x5+a6x6；令 x1，则 a0+a1+a2+a5+a6f（1）32（a+1）

22、，令 x1，则 a0a1+a2a5+a6f（1）0 +得，2（a0+a2+a4+a6）32（a+1），即 2832（a+1），求得 a 故答案为：【点评】本题考查解决展开式的系数和问题时，一般先设出展开式，再用赋值法代入特殊值，相加或相减，属于基础题 15过抛物线 y24x 焦点 F 的直线交抛物线于点 A、B，交准线于点 P，交 y 轴于点 Q，若，则弦长|AB| 【分析】设直线 AB 的方程为 yk（x1），A（x1，y1），B（x2，y2），将其与抛物线的方程联立，写出两根之和，然后分别把 x1 和 x0 代入 yk（x1）可得点 P 和 Q 的坐标，由于，借助平面向量的线性

23、坐标运算可解得，再将其代入到抛物线方程即可求得 k 的值，最后利用抛物线的定义求得焦点弦|AB|的长度解：设直线 AB 的方程为 yk（x1），A（x1，y1），B（x2，y2），联立得 k2x2（2k2+4）x+k2 0，，把 x1 代入 yk（x1）得 y2k，P（1，2k），把 x0 代入 yk（x1）得 yk，Q（0，k），，（1，k）（x21，y2），解得，点 B 在抛物线上，，，而，由抛物线的定义可知，|AB| 故答案为：【点评】本题考查抛物线的定义、直线与抛物线的位置关系，还涉及平面向量的线性坐标运算，考查学生的分析能力和运算能力，属于基础题

24、16九章算术卷第五商功中描述几何体“阳马”为“底面为矩形，一棱垂直于底面的四棱锥”现有阳马 SABCD，SA平面 ABCD，AB1，AD3，SA ，BC 上有一点 E，使截面 SDE 的周长最短，则 SE 与 CD 所成角的余弦值等于【分析】通过底面展开转化为平面图形，容易找到最小值点 E，然后利用平移法作出异面直线所成的角，不难求解解：将平面 ABCD 沿 BC 折至 ABCD，使 SBC 与 ABCD共面，连接 SD交 BC 于 E，连接 ED，此时SDE 周长最短，作 EFCD 交 AD 于 F，则SEF（或其补角）即为所求角，在 RtSAB 中，求得 SB2，

25、由得 BE2，在 RtSBE 中，求得 SE ，在 RtSFE 中，cosSEF ，故 SE 与 CD 所成角的余弦值等于故答案为：【点评】此题考查了侧面展开找最值，异面直线所成角，线面垂直等，难度适中三、解答题：（本大题满分 60 分.解答应写出文字说明、证明过程或演算步骤.） 17 在ABC中，三内角A， B， C对应的边分别为a， b， c，若B为锐角，且sinA+2sinB cos A （）求 C；（）已知 a2，，求ABC 的面积【分析】（）利用三角函数恒等变换的应用化简已知等式可得 sinBsin（ A），结合 B 为锐角，可求 B+A ，即可求解 C

26、的值；（）利用平面向量数量积的运算结合 a2，可得 ccosB4，又根据正弦定理及已知可求 cosB sinB ，联立可求 csinB2 ，进而根据三角形的面积公式即可计算得解解：（）sinA+2sinB cosA， sinB cosA sinA，可得 sinBsin（ A）， B A，或 B+（ A）B A， B 为锐角， B A，即 B+A ， C （），可得 cacos（B）8，可得 cacosB8， a2，可得：ccosB4，又根据正弦定理，及 A B，C a2，可得：，解得 csin（ B），可得 cosB sinB ，将代入，可得 2 csinB ，可得

27、csinB2 ， SABC acsinB 2 【点评】本题主要考查了三角函数恒等变换的应用，平面向量数量积的运算，正弦定理，三角形的面积公式在解三角形中的综合应用，考查了计算能力和转化思想，属于中档题 18如图，在三棱柱 ABCA1B1C1中，ACBC1CB90，A1AC60，D，E 分别为 A1A 和 B1C1的中点，且 AA1ACBC （）求证：A1E平面 BC1D；（）求平面 BC1D 与平面 ABC 所成锐二面角的余弦值【分析】（）先根据，可知四边形 A1DFE 为平行四边形，由此 A1EDF，进而得证；（）先证明 A1O平面 ABC，由此可以 O 为坐标原点

28、，射线 OA，OA1分别为 x 轴和 z 轴的正半轴，以平行于 BC 的直线为 y 轴，建立空间直角坐标系，求出平面 BC1D 与平面 ABC 的法向量，再利用向量的夹角公式得解解：（）如图 1，取线段 BC1的中点 F，连接 EF，DF， E 为 B1C1的中点，，又 D 为 AA1的中点，，，四边形 A1DFE 为平行四边形， A1EDF，又 DF 在平面 BC1D 内，A1E 不在平面 BC1D 内， A1E平面 BC1D；（）作 A1OAC 于点 O，由A1AC60，得AA1O30，，即 O 为 AC 的中点， ACBCC1B90， BCCA，BCCC1，又 CAC

29、C1C， BC平面 A1ACC1，从而有 BCA1O，又 A1OCA，CABCC， A1O平面 ABC，故可以点 O 为坐标原点，射线 OA，OA1分别为 x 轴和 z 轴的正半轴，以平行于 BC 的直线为 y 轴，建立空间直角坐标系，如图 2，令AA1ACBC2a，则，，，，，，，，，，，，，，，，，，，，，设平面 BC1D 的一个法向量为，，，则，可取，，，又平面 ABC 的一个法向量为，，，设平面 BC1D 与平面 ABC 所成锐二面角为，则，平面 BC1D 与平面 ABC 所成锐二面角的余弦值为【点评】

30、本题考查线面平行的判定以及利用空间向量求解二面角问题，考查逻辑推理能力及运算求解能力，属于中档题 19已知椭圆 C：的离心率是，原点到直线的距离等于，又知点 Q（0，3）（）求椭圆 C 的标准方程；（）若椭圆 C 上总存在两个点 A、B 关于直线 yx+m 对称，且 3 28，求实数 m 的取值范围【分析】（）由椭圆的离心率及原点到直线的距离及 a，b，c 之间的关系求出 a，b 的值，进而求出椭圆的方程；（）由题意设直线 AB 的方程与椭圆联立求出两根之和及两根之积，及判别式大于 0，可得参数的范围，进而求出 AB 中点的坐标，而中点在直线 yx+m 上，代入可得参数

31、的关系，再求以，再由题意可得 m 的范围解：（）由题意可得：，c2a2b2，且，解得：a24，b22，所以椭圆的方程为： 1；（）由题意设直线 AB 的方程为：yx+n，联立，整理可得：3x 24nx+2 （n22）0，由（4n）2432（n22）0 可得 n26，设 A（x1，x1+n），B（x2，x2+n），则 x1+x2 ，x1x2 ，又设 AB 的中点 M（x0，x0+n），则 x0 ，x0+n ，由于点 M 在直线 yx+m 上，所以 m，可得 n3m，代入 n26，可得 9m2 6，解得，因为（x1，x1+n3），（x2，x2+n3），所以 2

32、x1x2（n3）（x1+2）+（n3） 2 （n3） 2 ，由 3 28，得 3n 26n+1928，解得1n3，所以13m3，即1 ，由可得，所以实数 m 的取值范围为（，）【点评】本题考查求椭圆的标准方程，及直线与椭圆的综合，和数量积的应用，属于中档题 20为了提高生产线的运行效率，工厂对生产线的设备进行了技术改造为了对比技术改造后的效果，采集了生产线的技术改造前后各 20 次连续正常运行的时间长度（单位：天）数据，并绘制了如茎叶图：（）（1）设所采集的 40 个连续正常运行时间的中位数 m，并将连续正常运行时间超过 m 和不超过 m 的次数填入下面的列联表：超

33、过 m 不超过 m 改造前 a b 改造后 c d （2）根据（1）中的列联表，能否有 99%的把握认为生产线技术改造前后的连续正常运行时间有差异？附：K2 ， P（K2k） 0.050 0.010 0.001 k 3.841 6.635 10.828 （）工厂的生产线的运行需要进行维护，工厂对生产线的生产维护费用包括正常维护费、保障维护费两种对生产线设定维护周期为 T 天（即从开工运行到第 kT 天（k一、选择题*）进行维护生产线在一个生产周期内设置几个维护周期，每个维护周期相互独立在一个维护周期内，若生产线能连续运行，则不会产生保障维护费；若生产线不能连续运行，则产生保障维护费

34、经测算，正常维护费为 0.5 万元/次；保障维护费第一次为 0.2 万元/周期，此后每增加一次则保障维护费增加 0.2 万元现制定生产线一个生产周期（以 120 天计）内的维护方案：T30，k1，2，3，4 以生产线在技术改造后一个维护周期内能连续正常运行的频率作为概率，求一个生产周期内生产维护费的分布列及期望值【分析】（）（1）由茎叶图里面的数据得到中位数 m，列出表格如下图，（2）根据（1）的二维联表求出 K2判断即可；（II）120 天的一个生产周期内有 4 个维护周期，一个维护周期为 30 天，一个维护周期内，以生产线在技术改造后一个维护周期内能连续正常运行的频率作为概率

35、，得 p ，设一个生产周期内需要次维护，B（4，），故一个生产周期内保障维护 X 次的生产维护费为（0.12+0.1+2）万元，设一个生产周期内的生产维护费为 X 万元，则 X 可能取值为 2，2.2，2.6，3.2，4，写出分布列，求出数学期望即可解：（I）（1）由茎叶图的数据可得中位数 m ，根据茎叶图可得：a5，b15，c15，d5，超过 m 不超过 m 改造前 5 15 改造后 15 5 （2）根据（1）中的列联表， K2 ，有 99%的把握认为生产线技术改造前后的连续正常运行时间有差异；（II）120 天的一个生产周期内有 4 个维护周期，一个维护周期为

36、 30 天，一个维护周期内，以生产线在技术改造后一个维护周期内能连续正常运行的频率作为概率，得 p ，设一个生产周期内需要次维护，B（4，），正常维护费为 0.542 万元，保障维护费为首项为 0.2，公差为 0.2 的等差数列，共次维护需要的保障费为万元，故一个生产周期内保障维护 X 次的生产维护费为（0.12+0.1+2）万元，设一个生产周期内的生产维护费为 X 万元，则 X 可能取值为 2，2.2，2.6，3.2，4，则，，，，，则 X 的分布列为： X 2 2.2 2.6 3.2 4 P 故 E（X）2 2.2 万元，【点评】本题主要考查离散型随机变

37、量的分布列和数学期望，同时考查了茎叶图求中位数等，考查数学运算能力和实际应用能力，中档题 21已知函数，（）若 f（x）为 R 上的增函数，求 a 的取值范围；（）若 a0，x1x2，且 f（x1）+f（x2）4，证明：f（x1+x2）2 【分析】（）依题意，exx+a0 恒成立，即 exxa 恒成立，设 F（x）exx，利用导数求出函数 F（x）的最小值即可；（）设函数 h（x）f（x）+f（x），x0，利用导数可知 h（x）在（，0）上为减函数，则 h（x1）f（x1）+f（x1）h（0）4，进而得 f（x2）4f（x1）f （x1），再结合函数 f（x）的单调性即得证【解

38、答】（）解：f（x）exx+a，若 f（x）在 R 上为增函数，则 exx+a0 恒成立，即 exxa 恒成立，设 F（x）exx，则 F（x）ex1，当 x（，0）时，F（x）0，当 x（0，+）时，F（x）0， F（x）在（，0）上单调递减，在（0，+）上单调递增， F（x）F（0）1，故a1，实数 a 的取值范围为1，+）；（）证明：若 a0，由（）知 f（x）在 R 上单调递增，由于 f（0）2，已知 x1 x2，f（x1）+f（x2）4，不妨设 x10x2，设函数 h（x） f（x）+f （x），x0，则 ex+exx2+2，则 h（x）exex2x，设（x）h（x

39、），则（x）ex+ex20，由于 x0，故 h（x）在（，0）上为增函数， h（x）h（0）0， h（x）在（，0）上为减函数， h（x1）f（x1）+f（x1）h（0）4， f（x2）4f（x1）f（x1），而 f（x）在 R 上为增函数， x2x1，故 x1+x20，从而 f（x1+x2）02，即 f（x 1+x2）2 【点评】本题考查利用导数研究函数的单调性，考查不等式的证明，考查推理论证能力及运算求解能力，属于中档题请考生在第 22、23 题中任选一题作答，如果多做，则按所做的第一题记分作答时请写清题号选修 4-4：坐标系与参数方程 22在平面直角坐标系 xOy 中，曲线

40、C1的参数方程为（其中为参数），以原点 O 为极点，以 x 轴非负半轴为极轴建立极坐标系，曲线 C2的极坐标方程为 +4cos 0 （）求曲线 C1的普通方程与曲线 C2的直角坐标方程；（）设点 A，B 分别是曲线 C1，C2上两动点且AOB ，求AOB 面积的最大值【分析】（）直接利用转换关系，把参数方程极坐标方程和直角坐标方程之间进行转换（）利用极径的应用和三角形面积公式的应用求出结果解：（）曲线 C1的参数方程为（其中为参数），转换为直角坐标方程为（x3）2+y29 曲线 C2的极坐标方程为 +4cos0，转换为直角坐标方程为 x2+y2+4x0 （）由（）得：

41、曲线 C1的极坐标方程为 6cos，曲线 C2的极坐标方程为 4cos，设 A（1，），B（，），所以，当时，AOB 面积的最大值为 6 【点评】本题考查的知识要点：参数方程极坐标方程和直角坐标方程之间的转换，三角形面积公式的应用，三角函数关系式的恒等变换，正弦型函数的性质的应用，主要考查学生的运算能力和转换能力及思维能力，属于基础题型选修 4-5：不等式选讲 23已知函数 f（x）|xm|+|x |（其中实数 m0）（）当 m1，解不等式 f（x）3；（）求证：f（x） 2 【分析】（）可得 f（x）|x1|+|x |，由零点分区间和绝对值的意义，去绝对值，解不等式，求并集，可得所求解集；（）可结合绝对值不等式的性质和基本不等式，化简即可得证解：（）当 m1 时，f（x）|x1|+|x |，则 f（x）3 等价为或或，解得 1x 或 x1 或 x ，所以原不等式的解集为，；（）证明：由函数 f（x）|xm|+|x |（其中实数 m0），可得 f（x） |xm|+|x | |xmx | m m m 2 2，当且仅当 m1 时，上式等号成立于是原不等式成立【点评】本题考查绝对值不等式的解法，注意运用分类讨论思想，考查不等式的证明，注意运用绝对值不等式的性质和基本不等式，考查化简运算能力和推理能力，属于中档题