云南省玉溪市2019-2020学年普通高中毕业生第二次教学质量检测数学试卷（文科）含答案解析

《云南省玉溪市2019-2020学年普通高中毕业生第二次教学质量检测数学试卷（文科）含答案解析》由会员分享，可在线阅读，更多相关《云南省玉溪市2019-2020学年普通高中毕业生第二次教学质量检测数学试卷（文科）含答案解析（26页珍藏版）》请在七七文库上搜索。

1、2020 年云南省玉溪市高考数学二模试卷（文科）年云南省玉溪市高考数学二模试卷（文科） 一、选择题（共 12 小题）. 1已知集合 A2，0，2，4，Bx|log2x2，则 AB（ ） A 2，4 B2，2 C0，2，4 D2，0，2，4 2复平面内表示复数 z（1+i）（2+i）的点位于（ ） A第一象限 B第二象限 C第三象限 D第四象限 3sin25cos20cosl55sin20（ ） A B C D 4从数字 1，2，3，4，5 中任意取出两个不同数字，至少有一个是偶数的概率为（ ） A B C D 5直线 ax+y10 与圆 x2+y24x4y0 交于 A，B 两点，若|AB|4，

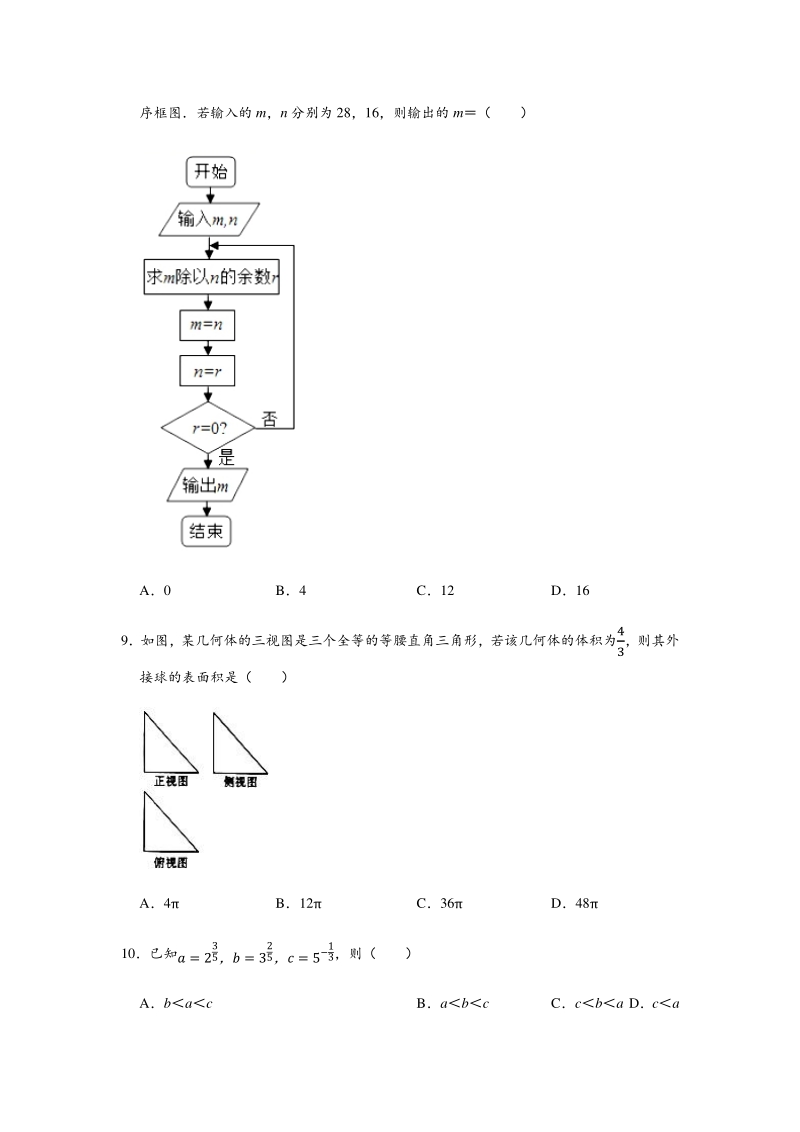
2、则 a（ ） A B C D 6若等差数列an的前 15 项和 S1530，则 2a5a6a10+a14（ ） A2 B3 C4 D5 7 设 ， ， 为三个不同的平面， m， n 是两条不同的直线， 则下列命题为假命题的是 （ ） A若 m，n，mn，则 B若 ，n，m，mn，则 m C若 m，m，则 D若 ，则 8如图，该程序框图的算法思路源于“辗转相除法”，又名“欧几里德算法”，执行该程 序框图若输入的 m，n 分别为 28，16，则输出的 m（ ） A0 B4 C12 D16 9如图，某几何体的三视图是三个全等的等腰直角三角形，若该几何体的体积为 ，则其外 接球的表面积是（ ） A4

3、B12 C36 D48 10已知 ， ， ，则（ ） Abac Babc Ccba D ca b 11已知双曲线 C： ， ， ，点 A 为双曲线 C 上一点， 且在第一象限，点 O 为坐标原点，F1，F2分别是双曲线 C 的左、右焦点，若|AO|c，且 AOF1 ，则双曲线 C 的离心率为（ ） A B C2 D 1 12设函数 ，已知方程 f（x）a（a 为常数）在0， 上恰有 三个根，分别为 x1，x2，x3（x1x2x3），下述四个结论： 当 a0 时， 的取值范围是 ， ）； 当 a0 时，f（x）在0， 上恰有 2 个极小值点和 1 个极大值点； 当 a0 时，f（x）在0， 上单

4、调递增； 当 2 时，a 的取值范围为 ，1），且 其中正确的结论个数为（ ） A1 B2 C3 D4 二、填空题（本大题共 4 小题，每小题 5 分，共 20 分将答案填在答题卡相应位置上） 13已知向量 （2，l）， （l，x），若| | |，则 x 14甲、乙、丙三位同学一起去向老师询问数学学科学业水平考试成绩，老师说：你们三人 中有 2 位优秀，1 位良好，我现在给甲看乙的成绩，乙看丙的成绩看后甲对大家说：我 还是不知道我的成绩乙听后对大家说：看完丙的成绩，我并不知道自己的成绩，但是 听甲这么说，现在知道了丙听甲和乙的话后说：听你们这么说，虽然我没看任何人的成 绩，但是我已经知道我的成

5、绩了，根据以上信息，判断成绩获得“优秀”的两名同学 是 15ABC 的内角 A，B，C 的对边分别为 a，b，c若 sinA ，b2+c26+a2，则ABC 的面积为 16已知 f（x）是定义域为 R 的奇函数，f（x）是 f（x）的导函数，f（1）0，当 x 0 时，xf（x）3f（x）0，则使得 f（x）0 成立的 x 的取值范围是 三、 解答题 （本大题共 5 小题， 共 70 分解答应写出必要的文字说明， 证明过程或演算步骤） 17在等比数列an中，a16，a212a3 （l）求an的通项公式； （2）记 Sn为an的前 n 项和，若 Sm66，求 m 18如图，长方体 ABCDA1B

6、1C1D1的侧面 A1ADD1是正方形 （1）证明：A1D平面 ABD1； （2）若 AD2，AB4，求点 B 到平面 ACD1的距离 19某商场为提高服务质量，随机调查了 60 名男顾客和 80 名女顾客，每位顾客均对该商场 的服务给出满意或 不满意的评价，得到下面不完整的列联表： 满意 不满意 合计 男顾客 50 女顾客 50 合计 （1）根据已知条件将列联表补充完整； （2）能否有 99%的把握认为男、女顾客对该商场服务的评价有差异？ 附：K2 P（K2k） 0.050 0.010 0.001 k 3.841 6.635 10.828 20如图，在平面直角坐标系中，已知点 F（2，0），

7、直线 l：x4，过动点 P 作 PH l 于点 H， HPF 的平分线交 x 轴于点 M， 且|PH| |MF|， 记动点 P 的轨迹为曲线 C （1）求曲线 C 的方程； （2）过点 N（0，2）作两条直线，分别交曲线 C 于 A，B 两点（异于 N 点）当直 线 NA，NB 的斜率之和为 2 时，直线 AB 是否恒过定点？若是，求出定点的坐标；若不 是，请说明理由 21已知函数 f（x）x1alnx （1）讨论 f（x）的单调性； （2）证明： ， 选考题请考生在第 22、23 两题中任选一题作答，并用 2B 铅笔在答题卡上把所选题目的题 号涂黑注意所做题目的题号必须与所涂题目的题号一致，

8、在答题卡选答区域指定位置答 题 如果多做， 则桉所做的第一题计分 选修 4-4： 坐标系与参数方程 （本小题满分 10 分） 22已知曲线 C： （ 为参数），设曲线 C 经过伸缩变换 ， 得到曲线 C， 以直角坐标中的原点 O 为极点，x 轴的正半轴为极轴建立极坐标系 （1）求曲线 C的极坐标方程； （2）若 A，B 是曲线 C上的两个动点，且 OAOB，求|OA|2+|OB|2的最小值， 选修 4-5：不等式选讲（本小题满分 0 分） 23已知函数 f（x）|x+2|+|x2|，M 为方程 f（x）4 的解集 （l）求 M； （2）证明：当 a，b M，|2a+2b|4+ab| 参考答案

9、一、选择题（本大题共 12 小题，每小题 5 分，共 60 分在每小题给出的四个选项中，只有 一项是符合题目要求的） 1已知集合 A2，0，2，4，Bx|log2x2，则 AB（ ） A 2，4 B2，2 C0，2，4 D2，0，2，4 【分析】可以求出集合 B，然后进行交集的运算即可 解：A2，0，2，4，Bx|0x4， AB2，4 故选：A 【点评】本题考查了列举法、描述法的定义，对数函数的定义域和单调性，交集的运算， 考查了计算能力，属于基础题 2复平面内表示复数 z（1+i）（2+i）的点位于（ ） A第一象限 B第二象限 C第三象限 D第四象限 【分析】利用复数的运算法则、几何意义即

10、可得出 解：z（1+i）（2+i）3i 的点（3，1）位于第三象限 故选：C 【点评】本题考查了复数的运算法则、几何意义，考查了推理能力与计算能力，属于基 础题 3sin25cos20cosl55sin20（ ） A B C D 【分析】根据诱导公式与两角和的正弦公式，计算即可 解：sin25cos20cosl55sin20sin25cos20+cos25sin20 sin（25+20） sin45 故选：B 【点评】本题考查了诱导公式与两角和的正弦公式应用问题，是基础题 4从数字 1，2，3，4，5 中任意取出两个不同数字，至少有一个是偶数的概率为（ ） A B C D 【分析】利用组合数公

11、式求出从数字 1，2，3，4，5 中任意取出两个不同数字和至少有 一个是偶数的选法，相比即可 解：从数字 1，2，3，4，5 中任意取出两个不同数字，有 C 10 种，两数都是奇数时 有 C 3 则至少有一个是偶数的概率为 P ， 故选：A 【点评】本题考查组合数公式，对立事件，属于基础题 5直线 ax+y10 与圆 x2+y24x4y0 交于 A，B 两点，若|AB|4，则 a（ ） A B C D 【分析】化圆的方程为标准方程，求出圆心坐标与半径，再求出圆心到直线的距离，利 用垂径定理列式求 a 值 解：由圆 x2+y24x4y0，得（x2）2+（y2）28， 则圆心坐标为（2，2），半径

12、为 圆心到直线 ax+y10 的距离 d ， |AB|4， ，解得 a 故选：D 【点评】本题考查直线与圆位置关系的应用，训练了利用垂径定理求弦长，是中档题 6若等差数列an的前 15 项和 S1530，则 2a5a6a10+a14（ ） A2 B3 C4 D5 【分析】利用等差数列的通项公式求和公式即可得出 解：S153015a8，解得 a82 2a5a6a4， a4+a14a10+a8 则 2a5a6a10+a14a82 故选：A 【点评】本题考查了等差数列的通项公式求和公式，考查了推理能力与计算能力，属于 基础题 7 设 ， ， 为三个不同的平面， m， n 是两条不同的直线， 则下列命

13、题为假命题的是 （ ） A若 m，n，mn，则 B若 ，n，m，mn，则 m C若 m，m，则 D若 ，则 【分析】根据空间中的直线与直线、直线与平面、以及平面与平面的位置关系，判断选 项中的命题是否正确即可 解：对于 A，由 m，n，且 mn，得出 ，所以 A 正确； 对于 B，由 ，n，m，mn，根据面面垂直的性质定理得出 m，所以 B 正确； 对于 C，由 m，m，根据面面垂直的判定定理得出 ，所以 C 正确； 对于 D，若 ，则 与 可能相交，也可能平行，所以 D 错误 故选：D 【点评】本题主要考查了空间中的垂直关系应用问题，也考查了推理与判断能力，是基 础题 8如图，该程序框图的算

14、法思路源于“辗转相除法”，又名“欧几里德算法”，执行该程 序框图若输入的 m，n 分别为 28，16，则输出的 m（ ） A0 B4 C12 D16 【分析】由已知中的程序语句可知：该程序的功能是利用循环结构计算并输出变量 m 的 值，模拟程序的运行过程，分析循环中各变量值的变化情况，可得答案 解：若输入的 m，n 分别为 28，16， 第一次循环：m16，n12，r12 第二次循环：m12，n4，r4 第三次循环：m4，n0，r0 结束循环，此时 m4 故选：B 【点评】本题考查了程序框图的应用问题，解题时应模拟程序框图的运行过程，以便得 出正确的结论，是基础题 9如图，某几何体的三视图是三

15、个全等的等腰直角三角形，若该几何体的体积为 ，则其外 接球的表面积是（ ） A4 B12 C36 D48 【分析】先由题设条件找出该几何体的直观图，把它镶嵌在正方体中，正方体的体对角 线就为该外接球的直径，计算出半径，解决其表面积问题 解：可以把题设中的几何体三棱锥 PABC 镶嵌在如右图所示的正方体中： 设正方体的棱长为 a，又 V三棱锥PABC a 2a ，解得：a2 正方体的体对角线就为该外接球的直径， 2R2 ，解得 R ，外接球的表面积为 4R212 故选：B 【点评】本题主要考查利用镶嵌法求几何体的外接球问题，属于基础题 10已知 ， ， ，则（ ） Abac Babc Ccba

16、D ca b 【分析】利用指数函数的性质求解 解： ， ， ba1， ，0c1， cab， 故选：D 【点评】本题主要考查了指数函数的性质，是基础题 11已知双曲线 C： ， ， ，点 A 为双曲线 C 上一点， 且在第一象限，点 O 为坐标原点，F1，F2分别是双曲线 C 的左、右焦点，若|AO|c，且 AOF1 ，则双曲线 C 的离心率为（ ） A B C2 D 1 【分析】 分别在AOF1和AOF2中， 通过简单的平面几何计算可求得|AF1|和|AF2|的长， 然后结合双曲线的定义，即可求得离心率 解：由题意可知，F1（c，0），F2（c，0）， 在AOF1中，|AO|c|OF1|，且A

17、OF1 ，|AF1| ， 在AOF2中，|AO|c|OF2|，且AOF2 ，|AF2|c， 由双曲线的定义可知，|AF1|AF2|2a，即 c2a， 离心率 故选：D 【点评】本题考查双曲线的定义、离心率，考查学生的运算能力，属于基础题 12设函数 ，已知方程 f（x）a（a 为常数）在0， 上恰有 三个根，分别为 x1，x2，x3（x1x2x3），下述四个结论： 当 a0 时， 的取值范围是 ， ）； 当 a0 时，f（x）在0， 上恰有 2 个极小值点和 1 个极大值点； 当 a0 时，f（x）在0， 上单调递增； 当 2 时，a 的取值范围为 ，1），且 其中正确的结论个数为（ ） A1

18、 B2 C3 D4 【分析】由 0x ，得 ，再由题意可得 3 4， 解不等式组即可求得 的范围判断； 作出函数 的图象的大致形状，由图判断错误； 当 x 0， 时， ，结合 的范围可得 ， 0， ， 则 f（x）在0， 上单调递增，故正确； 当 2 时， 2x ， 画出函数的大致图象， 由对称性可得 ， ， 即 ，故正确 解：当 0x 时， ， 此时 f（x）恰有 3 个零点，则 3 4， 解得 ，故正确： 作出函数 的图象的大致形状如图， 其中 m n 由图可知，f（x）在0， 上恰有 2 个极大值点和 1 个极小值点，故错误； 当 x 0， 时， ， ， ， 0， ，则 f（x）在0，

19、上单调递增，故正确； 当 2 时，2x ， 画出函数的大致图象： 由图可知，a 的取值范围为 ，1）， ， ， ，故正确 正确命题的个数为 3 故选：C 【点评】本题考查命题的真假判断与应用，考查 yAsin（x+）型函数的图象与性质， 考查数形结合的解题思想方法，是中档题 二、填空题（本大题共 4 小题，每小题 5 分，共 20 分将答案填在答题卡相应位置上） 13已知向量 （2，l）， （l，x），若| | |，则 x 2 【分析】本题先计算出向量 的坐标以及| |关于 x 的表达式，同理可计算出向量 的坐标以及| |关于 x 的表达式， 然后根据已知条件| | |， 代入进行计 算可得

20、x 的值 解：由题意，可知 （3，x1），则| | ， 同理， （1，1x），则| | ， | | |， ， 即 x22x+10x2+2x+2， 解得 x2 故答案为：2 【点评】本题主要考查向量的运算及模的计算考查了转化思想，定义法，逻辑思维能 力和数学运算能力本题属基础题 14甲、乙、丙三位同学一起去向老师询问数学学科学业水平考试成绩，老师说：你们三人 中有 2 位优秀，1 位良好，我现在给甲看乙的成绩，乙看丙的成绩看后甲对大家说：我 还是不知道我的成绩乙听后对大家说：看完丙的成绩，我并不知道自己的成绩，但是 听甲这么说，现在知道了丙听甲和乙的话后说：听你们这么说，虽然我没看任何人的成 绩

21、，但是我已经知道我的成绩了，根据以上信息，判断成绩获得“优秀”的两名同学是 乙和丙 【分析】根据甲和乙看完成绩之后都不知道自己成绩说明他们看到的都是优秀即可进行 判断 解：因为 3 人中有 2 个优秀，故甲和乙看到的成绩均是优秀，即乙是优秀，丙也是优秀， 故答案为：乙和丙 【点评】本题考查合情推理的应用，考查学生的推理能力，属于基础题 15ABC 的内角 A，B，C 的对边分别为 a，b，c若 sinA ，b2+c26+a2，则ABC 的面积为 【分析】先利用余弦定理求得 cosA ，由 sinA 的值求出 cosA，得到 bc 的值，从而利 用三角形面积公式求出ABC 的面积 解：由余弦定理

22、得：cosA 0， 又sinA ，cosA ， bc6， SABC ， 故答案为： 【点评】本题主要考查了余弦定理，以及三角形面积公式，是中档题 16已知 f（x）是定义域为 R 的奇函数，f（x）是 f（x）的导函数，f（1）0，当 x 0 时，xf（x）3f（x）0，则使得 f（x）0 成立的 x 的取值范围是 （， 1）（0，1） 【分析】首先利用当 x0 时，xf（x）3f（x）0，构造函数 ；f（x）是 定义域为 R 的奇函数，则函数 为偶函数，图象关于 y 轴对称，而且 g（1） f（1）0g（1），于是只需求出 x0 的单调性画图大致图象，在利用偶函数画 出 y 轴左边图象，即可

23、解决不等式 解：当 x0 时，令 ，则， 又当 x0 时，xf（x）3f（x）0， x0 时，g（x）0， g（x）在（0，+）上为减函数， 又f（x）是定义域为 R 的奇函数，则 x0 时， 为偶函数，且 g（1） f（1）0g（1）， 当 0x1 时， 0；当 x1 时， 0，则此时 f（x）0 成立 的 x 的取值范围是（0，1）； 当1x0 时， 0；当 x1 时， 0，则此时 f（x）0 成 立的 x 的取值范围是（，1）； 综上，f（x）0 成立的 x 的取值范围是（，1）（0，1） 【点评】本题主要突破点在于能利用题目条件构造出新的函数（一般条件为含有导数的 两个函数相减的这类整

24、体， 很大可能为某个分式函数的导数一部分， 再根据题目去构造） ， 考查了学生的构造法思想，以及函数性质的综合运用属于中档较难题目 三、 解答题 （本大题共 5 小题， 共 70 分解答应写出必要的文字说明， 证明过程或演算步骤） 17在等比数列an中，a16，a212a3 （l）求an的通项公式； （2）记 Sn为an的前 n 项和，若 Sm66，求 m 【分析】（1）设等比数列an的公比为 q，则 6q126q2，解得 q2 或 q1，由此 能求出 an （2）若 an6（2）n1，则 Sn 21（2） n，由 S m66，得 21 （2）m66，求出 m5；若 an6，q1，则an是常数

25、列，Sm6m66，求出 m 11由此能求出 m 的值 解：（1）设等比数列an的公比为 q， a16，a212a3 6q126q2，解得 q2 或 q1， 或 an6 （2）若 an6（2）n1， 则 Sn 21（2） n， 由 Sm66，得 21（2）m66，解得 m5 若 an6，q1，则an是常数列， Sm6m66，解得 m11 综上，m 的值为 5 或 11 【点评】 本题考查等比数列的通项公式、 项数的求法， 考查等比数列的性质等基础知识， 考查运算求解能力，是中档题 18如图，长方体 ABCDA1B1C1D1的侧面 A1ADD1是正方形 （1）证明：A1D平面 ABD1； （2）若

26、 AD2，AB4，求点 B 到平面 ACD1的距离 【分析】（1）在长方体 ABCDA1B1C1D1中，可知 ABA1D，再由四边形 A1ADD1 是正 方形，得 A1DAD1，利用直线与平面垂直的判定可得 A1D平面 ABD1； （2）设点 B 到平面 ACD1 的距离为 d，分别求出三角形 ABC 与三角形 ACD1 的面积， 再由 列式求解点 B 到平面 ACD1的距离 【解答】（1）证明：在长方体 ABCDA1B1C1D1中，AB平面 ADD1A1，A1D平面 ADD1A1， ABA1D， 四边形 A1ADD1 是正方形，A1DAD1， 又 ABAD1A， A1D平面 ABD1 （2）

27、解：设点 B 到平面 ACD1 的距离为 d， 由题意， ， 在长方体 ABCDA1B1C1D1中，D1D平面 ABCD，且 D1D2， ， 在ACD1中， ， ， ， ，得 d 点 B 到平面 ACD1的距离为 【点评】本题考查直线与平面垂直的判定，考查空间想象能力与思维能力，训练了利用 等体积法求点到平面的距离，是中档题 19某商场为提高服务质量，随机调查了 60 名男顾客和 80 名女顾客，每位顾客均对该商场 的服务给出满意或 不满意的评价，得到下面不完整的列联表： 满意 不满意 合计 男顾客 50 女顾客 50 合计 （1）根据已知条件将列联表补充完整； （2）能否有 99%的把握认为

28、男、女顾客对该商场服务的评价有差异？ 附：K2 P（K2k） 0.050 0.010 0.001 k 3.841 6.635 10.828 【分析】（1）根据已知条件即可把列联表补充完整； （2）计算 K 的观测值 K2，对照题目中的表格，得出统计结论 解：（1）列联表如下：不满意的评价，得到下面不完整的列联表： 满意 不满意 合计 男顾客 50 10 60 女顾客 50 30 80 合计 100 40 140 （2）K 的观测值：K2 7.292； 由于 7.2926.635， 有 99%的把握认为男、女顾客对该商场服务的评价有差异 【点评】本题考查了独立性检验的应用问题，也考查了计算能力的

29、应用问题，是基础题 目 20如图，在平面直角坐标系中，已知点 F（2，0），直线 l：x4，过动点 P 作 PH l 于点 H， HPF 的平分线交 x 轴于点 M， 且|PH| |MF|， 记动点 P 的轨迹为曲线 C （1）求曲线 C 的方程； （2）过点 N（0，2）作两条直线，分别交曲线 C 于 A，B 两点（异于 N 点）当直 线 NA，NB 的斜率之和为 2 时，直线 AB 是否恒过定点？若是，求出定点的坐标；若不 是，请说明理由 【分析】（1）设 P 的坐标，由题意可得 PHFM，所以HPMFMP，可得 ，即 ，整理可得 P 的轨迹方程； （2）分直线 AB 的斜率存在和不存在两

30、种情况讨论，当斜率存在时，设直线方程与椭圆 联立，求出两根之和及两根之积，求出直线 NA，NB 的斜率之和，由题意可得参数的关 系，代入直线方程可得直线 AB 恒过定点当直线的斜率不存在时，也成立 解：（1）设 P（x，y），由已知 PHFM，所以HPMFMP， 因为HPMFPM，所以FMPFPM，所以|MF|PF| 所以 ，即 ， 化简可得： 1， 所以曲线 C 的方程为： 1（y0） （2）当直线 AB 的斜率存在时，设其方程为：ykx+m（k0，m2），设 A（x1，y1）， B（x2，y2），联立直线与椭圆的方程 ，整理可得（1+2k 2）x2+4kmx+2m28 0，由0，x1+x2

31、 ，x 1x2 ， 由已知 kNA+kNB2，得 2， 整理可得 2（k1）x1x2+（m2）（x1+x2）0， 2（k1） （m2） 0，整理可得（m2） （4k2m4）0， 因为 m2，所以 m2k2， 所以直线 AB 的方程为：ykx+2k2k（x+2）2， 所以直线 AB 过定点（2，2）， 当直线 AB 的斜率不存在时，设方程为 xn，且 A（n，y1），B（n，y2）， 其中 y1y2， 由已知 kNA+kNB2，可得 2， 所以 n2， 所以直线 AB 的方程为 x2 此时直线 AB 也过定点（2，2）， 综上所述，直线 AB 恒过定点（2，2） 【点评】本题考查求椭圆的方程，及

32、直线与椭圆的综合和求证直线恒过定点的方法，属 于中档题 21已知函数 f（x）x1alnx （1）讨论 f（x）的单调性； （2）证明： ， 【分析】（1）f（x）x1alnxx （0，+）f（x）1 对 a 分类讨 论即可得出函数的单调性 （2）当 a1 时，f（x）x1lnx由（1）可得：f（x）f（1）0，可得 lnxx 1，当且仅当 x1 时，等号成立令 xn（n 一、选择题*，n2），可得 lnnn1于 是 进而证明结论 解：（1）f（x）x1alnxx （0，+） f（x）1 a0 时，f（x）0，函数 f（x）在（0，+）上单调递增 a0 时，令 f（x）0，解得 xa令 f（x

33、）0，解得 0xa 可得：函数 f（x）在（0，a）上单调递减，在（a，+）上单调递增 综上可得：a0 时，函数 f（x）在（0，+）上单调递增 a0 时，函数 f（x）在（0，a）上单调递减，在（a，+）上单调递增 （2）证明：当 a1 时，f（x）x1lnx 由（1）可得：f（x）f（1）0，lnxx1，当且仅当 x1 时，等号成立 令 xn（n N*，n2），lnnn1 （n N *，n2） 【点评】本题考查了利用导数研究函数的单调性极值与最值、方程与不等式的解法、分 类讨论方法、等价转化方法，考查了推理能力与计算能力，属于难题 选考题请考生在第 22、23 两题中任选一题作答，并用 2

34、B 铅笔在答题卡上把所选题目的题 号涂黑注意所做题目的题号必须与所涂题目的题号一致，在答题卡选答区域指定位置答 题 如果多做， 则桉所做的第一题计分 选修 4-4： 坐标系与参数方程 （本小题满分 10 分） 22已知曲线 C： （ 为参数），设曲线 C 经过伸缩变换 ， 得到曲线 C， 以直角坐标中的原点 O 为极点，x 轴的正半轴为极轴建立极坐标系 （1）求曲线 C的极坐标方程； （2）若 A，B 是曲线 C上的两个动点，且 OAOB，求|OA|2+|OB|2的最小值， 【分析】（1）直接利用参数方程极坐标方程和直角坐标方程之间的转换和伸缩变换的应 用求出结果 （2） 利用极径的应用和三角

35、函数关系式的恒等变换及正弦型函数的性质的应用求出结果 解：（1）曲线 C： （ 为参数），转换为直角坐标方程为 x 2+y24，曲线 C 经过伸缩变换 ， 得到曲线 C为 ，根据 转换为极坐标方 程为 （2）设 A（1，）B（ ， ）， 所以|OA|2+|OB|2 ， ， 当 sin21 时，|OA|2+|OB|2的最小值为 【点评】本题考查的知识要点：参数方程极坐标方程和直角坐标方程之间的转换，极径 的应用，三角函数关系式的恒等变换，正弦型函数的性质的应用，主要考查学生的运算 能力和转换能力及思维能力，属于基础题型 选修 4-5：不等式选讲（本小题满分 0 分） 23已知函数 f（x）|x+

36、2|+|x2|，M 为方程 f（x）4 的解集 （l）求 M； （2）证明：当 a，b M，|2a+2b|4+ab| 【分析】（1）由绝对值不等式的性质，可得所求解集 M； （2）运用分析法证明，结合两边平方和因式分解，以及不等式的性质，即可得证 解：（1）由 f（x）|x+2|+|x2|x+2x+2|4， 当且仅当（x+2）（x2）0 即2x2 时，等号成立， 则方程 f（x）4 的解集为 Mx|2x2； （2）证明：要证|2a+2b|4+ab|，只要证（2a+2b）2（4+ab）2， 即证 4a2+8ab+4b216+8ab+a2b2，即证 4a216+4b2a2b20， 即证（a24）（4b2）0， 因为 a，b M， 所以 a24，b24， 从而（a24）（4b2）0， 故原不等式成立 【点评】本题考查绝对值不等式的性质，注意函数方程的关系，考查不等式的证明，注 意运用分析法证明，考查化简运算能力和推理能力，属于中档题