2020年浙江省中考数学分类汇编专题12 锐角三角函数（含解析）

《2020年浙江省中考数学分类汇编专题12 锐角三角函数（含解析）》由会员分享，可在线阅读，更多相关《2020年浙江省中考数学分类汇编专题12 锐角三角函数（含解析）（12页珍藏版）》请在七七文库上搜索。

1、 2020 年浙江省中考数学分类汇编专题年浙江省中考数学分类汇编专题 12 锐角三角函数锐角三角函数 一、单选题一、单选题 1.如图，菱形 OABC 的顶点 A，B，C 在O 上，过点 B 作O 的切线交 OA 的延长线于点 D。若 O 的半径为 1，则 BD 的长为( ) 【来源：21cnj*y.co*m】 A. 1 B. 2 C. D. 2.如图，在离铁塔 150 米的 A 处，用测倾仪测得塔顶的仰角为 ，测倾仪高 AD 为 1.5 米，则铁塔 的高 BC 为( ) 【出处：21 教育名师】 A. (1.5+150tan) 米 B. (1.5+ )米 C. (1.5+150sin)米 D.

2、 (1.5+ ) 米【版权所有：21 教育】 3.已知二次函数 y=x ，当 axb 时 myn，则下列说法正确的是( ) A. 当 n-m=1 时，b-a 有最小值 B. 当 n-m=1 时，b-a 有最大值 C. 当 b-a=1 时，n-m 无最小值 D. 当 b-a=1 时，n-m 有最大值 4.如图，在 ABC 中，C=90 ，设A，B，C 所对的边分别为 a，b，c，则( )。 A. c=bsinB B. b=csinB C. a=btanB D. b=ctanB 二、填空题二、填空题 5.如图，已知边长为 2 的等边三角形 ABC 中，分别以点 A，C 为圆心，m 为半径作弧，两弧

3、交于 点 D，连结 BD。若 BD 的长为 2 ，则 m 的值为_。 2-1-c-n-j-y 6.如图是小明画的卡通图形，每个正六边形的边长都相等，相邻两正六边形的边重合，点 A，B， C 均为正六边形的顶点，AB 与地面 BC 所成的锐角为 ，则 tan 的值是_. 三、综合题三、综合题 7.人字折叠梯完全打开后如图 1 所示，B，C 是折叠梯的两个着地点，D 是折叠梯最高级踏板的固 定点. 图 2 是它的示意图，AB=AC，BD=140cm，BAC=40 ，求点 D 离地面的高度 DE. （结果精确到 0. 1cm；参考数据 sin700. 94，cos700. 34，sin200. 34

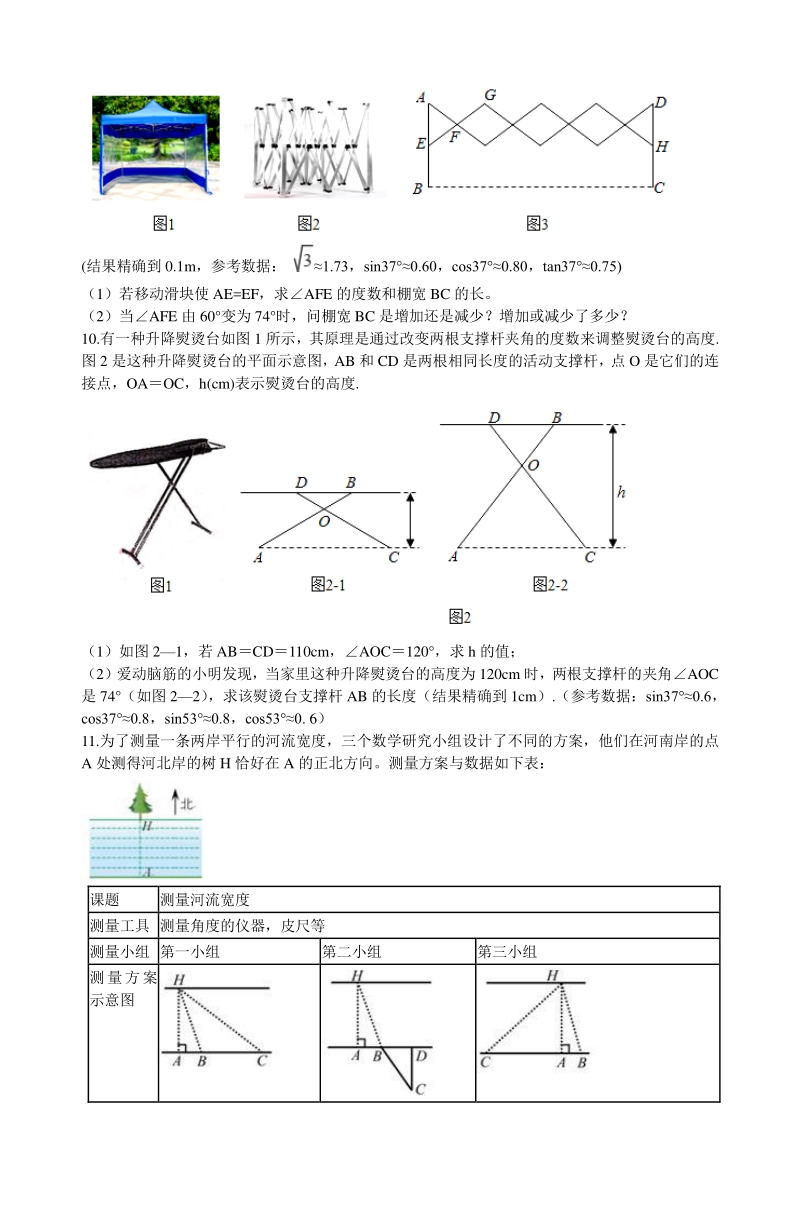
4、，cos200. 94） 8.如图，C，D 为O 上两点，且在直径 AB 两侧，连结 CD 交 AB 于点 E，G 是 上一点， ADC=G。 （1）求证：1=2。 （2） 点 C 关于 DG 的对称点为 F， 连结 CF.当点 F 落在直径 AB 上时， CF=10， tan1= ， 求O 的半径。 21*cnjy*com 9.如图 1 为搭建在地面上的遮阳棚，图 2、图 3 是遮阳棚支架的示意图。遮阳棚支架由相同的菱形 和相同的等腰三角形构成，滑块 E，H 可分别沿等长的立柱 AB，DC 上下移动，AF=EF=FG=1m。 (结果精确到 0.1m，参考数据： 1.73，sin370.60，

5、cos370.80，tan370.75) （1）若移动滑块使 AE=EF，求AFE 的度数和棚宽 BC 的长。 （2）当AFE 由 60 变为 74 时，问棚宽 BC 是增加还是减少？增加或减少了多少？ 10.有一种升降熨烫台如图 1 所示，其原理是通过改变两根支撑杆夹角的度数来调整熨烫台的高度. 图 2 是这种升降熨烫台的平面示意图，AB 和 CD 是两根相同长度的活动支撑杆，点 O 是它们的连 接点，OAOC，h(cm)表示熨烫台的高度. （1）如图 21，若 ABCD110cm，AOC120 ，求 h 的值； （2）爱动脑筋的小明发现，当家里这种升降熨烫台的高度为 120cm 时，两根支

6、撑杆的夹角AOC 是 74 （如图 22） ，求该熨烫台支撑杆 AB 的长度（结果精确到 1cm）.（参考数据：sin370.6， cos370.8，sin530.8，cos530. 6） www-2-1-cnjy-com 11.为了测量一条两岸平行的河流宽度，三个数学研究小组设计了不同的方案，他们在河南岸的点 A 处测得河北岸的树 H 恰好在 A 的正北方向。测量方案与数据如下表： 课题 测量河流宽度 测量工具 测量角度的仪器，皮尺等 测量小组 第一小组 第二小组 第三小组 测量方案 示意图 说明 点 B， C 在点 A 的正东方 向 点 B，D 在点 A 的正东 方向 点 B 在点 A 的

7、正东方向， 点 C 在点 A 的正西方向 测量数据 BC=60m， ABH=70 ， ACH=35 BD=20m， ABH=70 ， BCD=35 BC=101m， ABH=70 ， ACH=35 (参考数据：sin700.94，sin350.57，tan702.75，tan350.70)21*cnjy*com （1）哪个小组的数据无法计算出河宽？ （2）请选择其中一个方案及其数据求出河宽(精确到 0.1m)。 12.图1是一种三角车位锁， 其主体部分是由两条长度相等的钢条组成.当位于顶端的小挂锁打开时， 钢条可放入底盒中(底盒固定在地面下)，此时汽车可以进入车位；当车位锁上锁后，钢条按图 1

8、 的 方式立在地面上，以阻止底盘高度低于车位锁高度的汽车进入车位.图 2 是其示意图，经测量，钢 条 AB=AC=50cm， . 【来源：21世纪教育网】 （1）求车位锁的底盒长 BC. （2）若一辆汽车的底盘高度为 30cm，当车位锁上锁时，问这辆汽车能否进入该车位? (参考数据： ， ， ) 答案解析部分答案解析部分 一、单选题 1.答案: D 解：连接 ， 四边形 是菱形， ， ， ， ， 是 的切线， ， ， ， 故答案为： 【分析】连接 OB，利用菱形的性质可证得AOB=60 ，利用切线的性质，可证得DBO=90 ，再 利用解直角三角形求出 BD 的长。21 教育网 2.答案: A

9、解：过点 作 ， 为垂足，如图所示： 则四边形 为矩形， ， ， 在 中， ， ， ， 故答案为： 【分析】过点 A 作 AEBC 于点 E，易证四边形 CEAD 是矩形，就可求出 CE 的长，再利用解直 角三角形求出 BE 的长，然后根据 BC=CE+BE，代入计算可求解。 3.答案: B 解：当 ba1 时，如图 1， 过点 B 作 BCAD 于 C， BCD90 ， ADEBED90 ， ADDBCDBED90 ， 四边形 BCDE 是矩形， BCDEba1，CDBEm， ACADCDnm， 在 Rt ACB 中，tanABCnm， 点 A，B 在抛物线 yx2上， 0ABC90 ， t

10、anABC0， nm0， 即 nm 无最大值，有最小值，最小值为 0，故选项 C，D 都错误； 当 nm1 时，如图 2， 过点 N 作 NHMQ 于 H， 同的方法得，NHPQba，HQPNm， MHMQHQnm1， 在 Rt MHQ 中，tanMNH， 点 M，N 在抛物线 yx2上， m0， 当 m0 时，n1， 点 N（0，0） ，M（1，1） ， NH1， 此时，MNH45 ， 45MNH90 ， tanMNH1， 1ba1， ba 无最小值，有最大值，最大值为 1，故选项 A 错误； 故答案为：B 【分析】当 ba1 时，先判断出四边形 BCDE 是矩形，得出 BCDEba1，CD

11、BEm， 进而得出 ACnm，即 tannm，再判断出 0ABC90 ，即可得出 nm 的范围；当 nm 1 时，同的方法得出 NHPQba，HQPNm，进而得出 MHnm1，而 tanMHN 的值，再判断出 45MNH90 ，即可得出结论。 4.答案: B 解：C=90 sinB= ，tanB= b=csinB，b=atanB 故答案为：B 【分析】利用锐角三角函数的定义，分别对各选项进行计算，可得结果。 二、填空题 5.答案: 2 或 解：由作图知，点 在 的垂直平分线上， 是等边三角形， 点 在 的垂直平分线上， 垂直平分 ， 设垂足为 ， ， ， 当点 、 在 的两侧时，如图， ， ，

12、 ， ； 当点 、 在 的同侧时，如图， ， ， ， ， 综上所述， 的值为 2 或 ， 故答案为：2 或 【分析】根据作图可知点 D 和点 B 在 AC 的垂直平分线上，利用垂直平分线的性质及等边三角形 的性质，利用解直角三角形求出 BE 的长，再分情况讨论：当点 D，B 在 AC 的两侧时；当点 B， D 在 AB 的同侧时，分别求出 m 的值即可。21 教育名师原创作品 6.答案: 【解答】如图，过作 ADBC，过点 B 作 BHAD 垂足为 H，A=， 设正六边形的边长为 a，BH=6 2a=12a，AED=120 ，AE=AD=a， 在等腰三角形 ADE 中，ADE=EAD=30 ，

13、 AD=a，AH=a+a+a=a, tan=tanA=. 故答案为：. 【分析】如图，过作 ADBC，过点 B 作 BHAD 垂足为 H，可得A=，设正六边形的边长为 a，根据正六边形的性质及卡通图形，可得 BH=12a，ADE=EAD=30 ，AE=AD=a，从而求出 AD=a，从而可得 AH=a，由 tan=tanA=即可求出结论. 三、综合题 7.答案: 解：过点 A 作 AFBC 于点 F，则 AFDE， BDEBAF， ABAC，BAC40 ， BDEBAF20 ， DEBDcos201400.94131.6（cm） 答：点 D 离地面的高度 DE 约为 131.6cm 【分析】 过

14、点A作AFBC于点F， 根据等腰三角形的三线合一性质得BAF的度数， 进而得BDE 的度数，再解直角三角形得结果21 cn jy com 8.答案: （1）证明：ADC=G， AB 为O 的直径， ， 即 1=2。 （2）解：连结 DF ，AB 为O 的直径， ABCD， CE=DE， FD=FC=10 点 C，F 关于 GD 对称， DC=DF=10，DE=5 tan1= EB=DE tan1=2 1=2， tan2= ，AE= AB=AE+EB= ，O 的半径为 【分析】 （1）利用圆周角定理可证得弧 AC=弧 AD，再利用 AB 是圆的直径，去证明弧 CB=弧 BD， 然后根据等弧所对的

15、圆周角相等可证得结论。 （2）连接 DF，利用垂径定理可证得 CE=DE，ABCD，就可求出 DF，DE 的长，再利用解直角 三角形求出 EB，AE 的长，然后根据 AB=AE+EB，就可求出 AB 的长，即可得到圆的半径。 9.答案: （1）解： ， 是等边三角形， ， 连接 并延长交 于 ， 则 ， 是等边三角形， ， ， ， ； （2）解： ， ， ， ， ， ， 答：当 由 变为 时，棚宽 是减少了，减少了 【分析】 （1）由题意可知AEF 是等边三角形，利用等边三角形的性质，可证得AFE 的度数， 连接 MF 并延长交 AE 于点 K，可得 FM=2FK，可得到 AK 的长，再利用勾

16、股定理求出 FK 的长， 从而可求出 FM 的长，然后求出 BC 的长。 （2）利用已知求出AFK 的度数，利用解直角三角形求出 KF，FM 的长，再求出 BC 的长，然 后求差即可。www.21-cn- 10.答案: （1）解:过点 B 作 BEAC 于点 E，如图 2-1 OA=OC，AOC=120 ，OAC=OCA= =30 h=BE=AB sin30 =110 =55 （2）解:过点 B 作 BEAC 于点 E，如图 2-2， OA=OC，AOC=74 ，OAC=OCA= =53 AB=BEsin 531200.8=150(cm)。 即该熨烫台支撑杆 AB 的长度约为 150cm。 【

17、分析】 （1）过点 B 作 BEAC 于点 E，利用等腰三角形的性质及三角形内角和定理求出OAC 和OCA 的度数，再利用解直角三角形求出 BE 的长。 （2） 过点B作 BEAC于点 E， 利用等腰三角形的性质及三角形内角和定理求出OAC和OCA 的度数，然后利用解直角三角形求出 AB 的长。21 世纪教育网版权所有 11.答案: （1）答：第 2 小组的数据无法计算出河宽； （2）解：选第一小组的数据 ABH=ACH+BHC 70 =35 +BHC BHC=35 BHC=BCH HB=BC=60 在 Rt ABH 中， . 答：河宽为 56.4m. 2 1 c n j y 【分析】 （1）

18、根据表中的数据和图形可得答案。 （2）利用三角形内角和定理求出BHC，BCH 的度数，再利用解直角三角形求出 AH 的长。 12.答案: （1）解：过点 A 作 AHBC 于点 H， AB=AC， BH=HC， 在 Rt ABH 中，B=47 ，AB=50， BH=ABcosB=50cos 47500.68=34， BC=2BH=68cm （2）解：在 Rt ABH 中， AH=ABsinB=50sin47500.73=36.5(cm) ， 36.530， 当车位锁上锁时，这辆汽车不能进入该车位 【分析】 （1） 过点 A 作 AHBC 于点 H， 根据等腰三角形的性质可知 BH=HC，再利用三角函 数知识求出 BH，则 BC 长可求； （2）利用三角形函数知识求出 AH，由于汽车底盘低于车位锁底边 BC 上的高 AH，可知上锁时， 这辆汽车不能进入该车位.21世纪*教育网