2020年浙江省中考数学分类汇编专题09 圆（含解析）

《2020年浙江省中考数学分类汇编专题09 圆（含解析）》由会员分享，可在线阅读，更多相关《2020年浙江省中考数学分类汇编专题09 圆（含解析）（16页珍藏版）》请在七七文库上搜索。

1、 2020 年浙江省中考数学分类汇编专题年浙江省中考数学分类汇编专题 09 圆圆 一、单选题一、单选题 1.如图，点 A，B，C，D，E 均在O 上，BAC=15 ，CED=30 ，则BOD 的度数为（ ） A. 45 B. 60 C. 75 D. 90 2.如图，已知四边形 ABCD 内接于O，ABC70 ，则ADC 的度数是（ ） A. 70 B. 110 C. 130 D. 140 3.如图，已知 OT 是 Rt ABO 斜边 AB 上的高线，AOBO，以 O 为圆心，OT 为半径的圆交 OA 于点 C，过点 C 作O 的切线 CD，交 AB 于点 D，则下列结论中错误的是（ ） A.

2、DCDT B. AD DT C. BDBO D. 2OC5AC 4.如图，在等腰 ABC 中， AB=AC=2 ，BC=8， 按下列步骤作图： 以点 A 为圆心，适当的长度为半径作弧，分别交 AB，AC 于点 E，F，再分别以点 E，F 为圆心， 大于 EF 的长为半径作弧相交于点 H，作射线 AH；分别以点 A，B 为圆心，大于 AB 的 长为半径作弧相交于点 M，N，作直线 MN，交射线 AH 于点 0；以点为圆心，线段 OA 长为半 径作圆。则O 的半径为( ) A. 2 B. 10 C. 4 D. 5 5.如图，已知 BC 是O 的直径，半径 OABC，点 D 在劣弧 AC 上(不与点

3、 A，点 C 重合)，BD 与 OA 交于点 E，设AED=，AOD=，则( ) 2 1 c n j y A. 3+=180 B. 2+=180 C. 3-=90 D. 2-=90 6.如图，O 是等边 ABC 的内切圆，分别切 AB，BC，AC 于点 E，F，D，P 是 上一点，则 EPF 的度数是（ ） 【版权所有：21 教育】 A. 65 B. 60 C. 58 D. 50 二、填空题二、填空题 7.如图，在 ABC 中，D 是边 BC 上的一点，以 AD 为直径的O 交 AC 于点 E，连接 DE. 若O 与 BC 相切，ADE=55 ，则C 的度数为_ . 8.若扇形的圆心角为 45

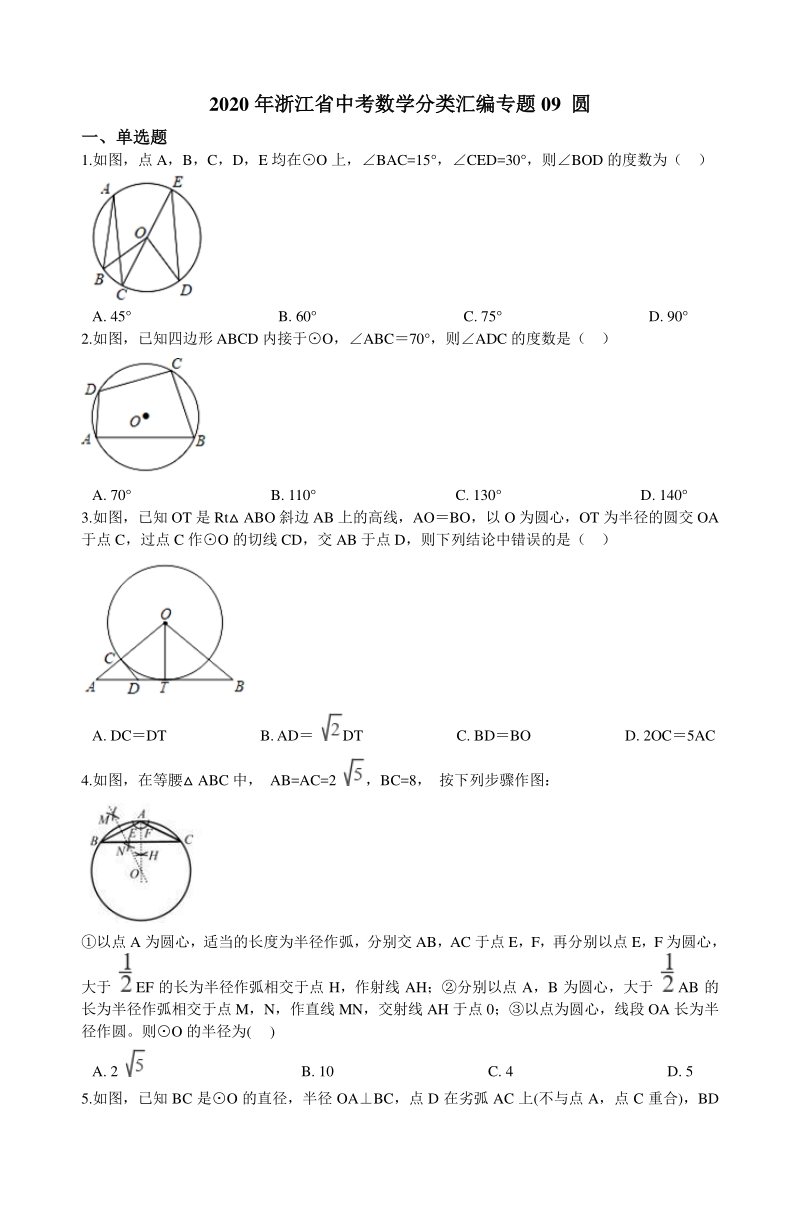
4、 ，半径为 3，则该扇形的弧长为_。 9.如图，已知 AB 是半圆 O 的直径，弦 CDAB，CD8，AB10，则 CD 与 AB 之间的距离是 _. 10.如图，在半径为 的圆形纸片中，剪一个圆心角为 90 的最大扇形(阴影部分)，则这个扇形的 面积为_；若将此扇形围成一个无底的圆锥(不计接头)，则圆锥底面半径为_ 。 11.如图，已知 AB 是O 的直径，BC 与O 相切于点 B，连接 AC，OC，若 sinBAC= ，则 tanBOC=_。 12.如图， O 的半径 OA=2， B 是O 上的动点(不与点 A 重合)， 过点 B 作O 的切线 BC， BC=OA， 连结 OC，AC.当

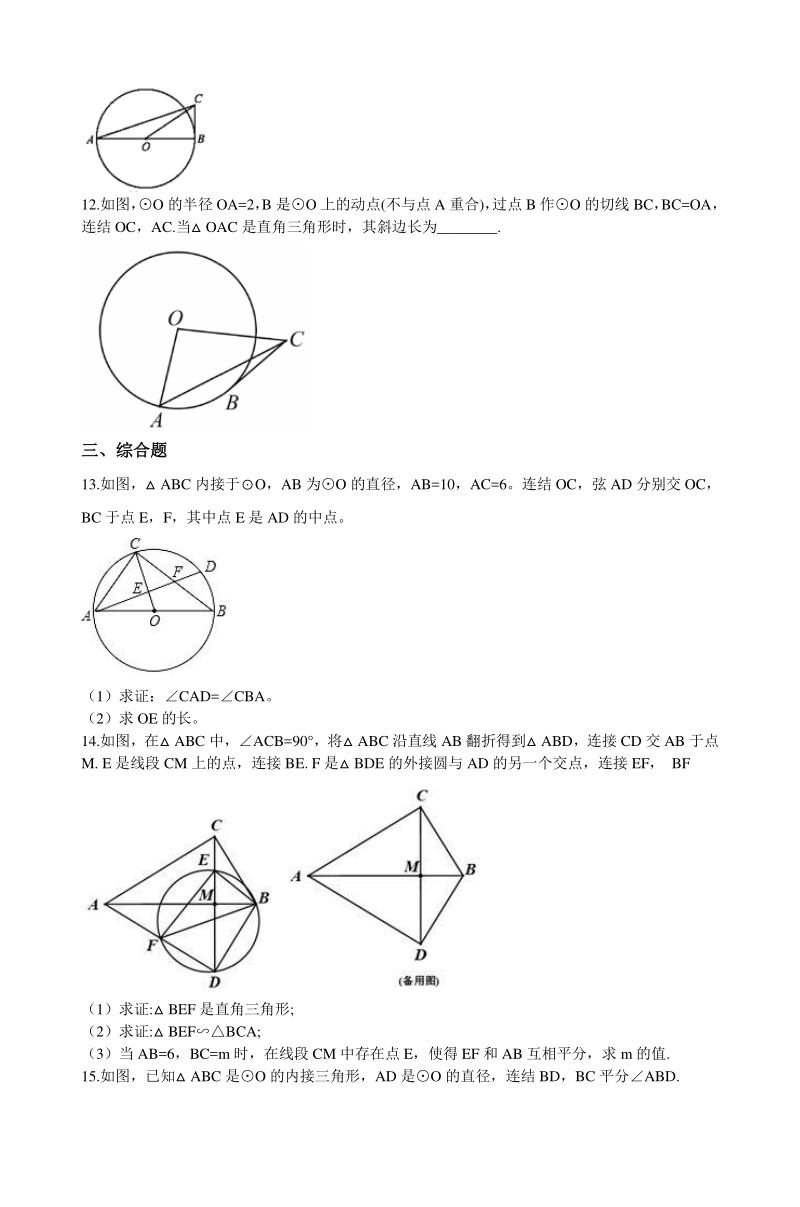
5、OAC 是直角三角形时，其斜边长为_. 三、综合题三、综合题 13.如图， ABC 内接于O，AB 为O 的直径，AB=10，AC=6。连结 OC，弦 AD 分别交 OC， BC 于点 E，F，其中点 E 是 AD 的中点。 【来源：21世纪教育网】 （1）求证：CAD=CBA。 （2）求 OE 的长。 14.如图，在 ABC 中，ACB=90 ，将 ABC 沿直线 AB 翻折得到 ABD，连接 CD 交 AB 于点 M. E 是线段 CM 上的点，连接 BE. F 是 BDE 的外接圆与 AD 的另一个交点，连接 EF， BF （1）求证: BEF 是直角三角形; （2）求证: BEFBCA

6、; （3）当 AB=6，BC=m 时，在线段 CM 中存在点 E，使得 EF 和 AB 互相平分，求 m 的值. 15.如图，已知 ABC 是O 的内接三角形，AD 是O 的直径，连结 BD，BC 平分ABD. （1）求证：CADABC； （2）若 AD6，求 的长. 16.已知：如图，在 OAB 中，OA=OB，O 与 AB 相切于点 C。求证：AC=BC。 小明同学的证明过程如下框： 证明：连结 OC OA=OB，A=B 又OC=OC， OACOBC， AC=BC 小明的证法是否正确？若正确，请在框内打“”；若错误，请写出你的证明过程。 17.如图， 的半径 OA=2，OCAB 于点 C，

7、AOC60 . （1）求弦 AB 的长. （2）求 的长. 18.如图，已知 AC，BD 为O 的两条直径，连接 AB，BC，OEAB 于点 E，点 F 是半径 OC 的 中点，连接 EF. 21*cnjy*com （1）设O 的半径为 1，若BAC=30 ，求线段 EF 的长。 （2）连接 BF，DF 求证：PE=PF 若 DF=EF，求BAC 的度数。 答案解析部分答案解析部分 一、单选题 1.【答案】 D 解：连接 ， ， ， ， 故答案为：D 【分析】连接 BE，利用同弧所对的圆周角相等，可求出BEC 的度数，从而可求出BED 的度 数，然后利用圆周角定理求出BOD 的度数。21 教育

8、名师原创作品 2.【答案】 B 解： 四边形 内接于 ， ， ， 故答案为：B. 【分析】利用圆内接四边形的对角互补，就可求出ADC 的度数。 3.【答案】 D 解：如图，连接 . 是半径， ， 是 的切线， 是 的切线， ， 正确， ， ， ， 是切线， ， ， ， ， ， 正确， ， ， ， ， ， ， ， ， ， ， ， ， 正确， 故答案为：D. 【分析】连接 OD，利用切线的判定定理可证得 DT 是圆的切线，再利用切线长定理可对 A 作出 判断；再证明 ADC 是等腰直角三角形，利用解直角三角形可得到 AD 和 CD 的数量关系，可对 B 作出判断；再证明 DOCDOT，利用全等三角

9、形的性质，可证得DOC=DOT，然后求出 BOD 和CDB 的度数，就可推出 BD=BO，可对 C 作出判断；从而可得到错误的选项。 4.【答案】 D 解：设 AO 与 BC 交于点 L，连接 OC AOBC 在 Rt ALC 中， , 设圆的半径为 r，则 OL=r-2 在 Rt OCL 中，OC2=OL2+CL2, r2=（r-2）2+42 解之：r=5. 故答案为：D 【分析】 设 AO 与 BC 交于点 L，连接 OC，利用垂径定理求出 CL 的长，再利用勾股定理求出 AL 的长，设圆的半径为 r，则 OL=r-2，利用勾股定理建立关于 r 的方程，解方程求出 r 的值。 5.【答案】

10、 D 解：如图，连接 AB 则DBA= DOA= 且DEA=DBA+OAB= OA=OB，BOA=90 ，即OAB=45 = +45 化简后得 2-=90 即 D 选项为正确选项 故答案为：D 【分析】利用一条弧所对的圆周角等于圆心角的一半，可得到DBA= ，利用三角形的外角 的性质，可证得DBA+OAB=，再证明OAB=45 ，继而可得到 和 之间的关系式。 6.【答案】 B 解：连接 OE，OF， 点 EF 分别是切点，OEB=OFB=90 ， ABC 是等边三角形，B=60 ， EOF=360 -OEB-OFB-B=120 ， P=EOF=60 . 故答案为：B. 【分析】连接 OE，O

11、F，根据切线的性质可得OEB=OFB=90 ，利用等边三角形的性质可得 B=60 ， 根据四边形内角和等于 360 ， 可求出EOF 的度数， 根据圆周角定理可得P=EOF， 据此求出结论.21*cnjy*com 二、填空题 7.【答案】 55 解：AD 为O 的直径， AED90 ， ADE+DAE90 ； O 与 BC 相切， ADC90 ， C+DAE90 ， CADE， ADE55 ， C55 故答案为：55 【分析】由直径所对的圆周角为直角得AED90 ，由切线的性质可得ADC90 ，然后由同 角的余角相等可得CADE55 21 教育网 8.【答案】 解：根据弧长公式： ， 故答案为

12、： 【分析】利用弧长公式：， 代入计算可求解。 9.【答案】 3 解：过点 作 于 ，连接 ，如图， 则 ， 在 中， ， 所以 与 之间的距离是 3. 故答案为 3. 【分析】过点 O 作 OHCD 于点 H，连接 OC，利用垂径定理求出 CH 的长，再利用勾股定理求 出 OH 的长。21 cn jy com 10.【答案】 ； 解：如图，连接 AB C=90 ，AC=BC AB 是直径 AB=， 在 Rt ACB 中， AC=ABsin45 =2 S 扇形 ACB=； 设扇形 ACB 的弧长为 l 解之：l=， 设底面圆的半径为 r 解之： 故答案为：. 【分析】连接 AB，利用圆周角定理

13、可证得 AB 的直径，同时可求出 AB 的长，再利用直角三角 形求出 AC 的长，利用扇形的面积公式求出扇形 ACB 的面积；设扇形 ACB 的弧长为 l，利用扇形 的面积公式求出弧长 l，然后根据圆锥展开图的扇形的弧长等于底面圆的周长，即可求出圆锥的底 面圆的半径。 11.【答案】 解：BC 与O 相切于点 B CBA=90 sinBAC= 设 BC=X，AC=3x AB= AO=OB= AB= x tanBOC= 故答案为： 【分析】利用切线的性质，可知CBA=90 ，再利用锐角三角函数的定义设 BC=X，AC=3x，利用 勾股定理用含 x 的代数式表示出 AB，OB 的长，然后就可求出

14、tanBOC 的值。 12.【答案】 2 或 2 解：如图，连接 OB， OA=OB，OA=BC， BC=OC=2， BC 为切线， OBBC， OC=， 当 AC 为斜边， AOC=90 ， AC=， 当 OC 为斜边， OC=2. 故答案为： 2 或 2 . 【分析】连接 OB，利用切线的性质，结合同圆的半径相等，利用勾股定理求出 OC 的长，然后 在 AOC 中，分别设 OC 和 AC 为斜边求值即可.21世纪*教育网 三、综合题 13.【答案】 （1）证明：AEDE，OC 是半径， ， CAD=CBA （2）解：AB 为O 的直径， ACB=90 AEDE， OCAD， AEC=90

15、. AEC=ACB 又CAD=CBA， ACEBAC， ， CE=3.6 又OC= AB=5， OEOCEC53.61.4 【分析】 （1）利用垂径定理以及圆周角定理解决问题即可 （2）证明 AECBCA ， 推出 ，求出 EC 即可解决问题21 世纪教育网版权所有 14.【答案】 （1）解：EFB=EDB，EBF=EDF EFB+EBF=EDB+EDF=90 FEB=90 ， BEF 为直角三角形 （2）解：BCBD， BDCBCD， EFBEDB， EFBBCD， ACAD，BCBD， ABCD， AMC90 ， BCD+ACDACD+CAB90 ， BCDCAB， BFECAB， ACB

16、FEB90 ， BEFBCA （3）解：设 EF 交 AB 于 J连接 AE EF 与 AB 互相平分， 四边形 AFBE 是平行四边形， EFAFEB90 ，即 EFAD， BDAD， EFBD， AJJB， AFDF， FJ BD ， EFm， ABCCBM， BC：MBAB：BC， BM ， BEJBME， BE：BMBJ：BE， BE ， BEFBCA， ， 即 ， 解得 m （负根已经舍弃） 【分析】（1） 想办法证明BEF90 即可解决问题 （也可以利用圆内接四边形的性质直接证明） （2） 根据两角对应相等两三角形相似证明 （3）证明四边形 AFBE 是平行四边形，推出 FJ BD

17、 ，EFm，由 ABCCBM，可得 BM ，由 BEJ BME，可得 BE ，由 BEFBCA，推出 ，由此构建方程求解即可www-2-1-cnjy-com 15.【答案】 （1）证明BC 平分ABD， DBC=ABC CAD=DBC CAD=ABC （2）解CAD=ABC， AD 是O 的直径，AD=6， 【分析】 （1）利用角平分线的定义可得到DBC=ABC，再利用同弧所对的圆周角相等，可得到 CAD=DBC，据此可证得结论。 （2）利用CAD=ABC，可证得弧 CD 和半圆的关系，根据圆的直径可得到圆的半径长，然后 就可求出弧 CD 的长。2-1-c-n-j-y 16.【答案】 小明的证

18、法错误. 证明：连接 OC， AB 是圆 O 的切线， OCAB， OA=OB， AC=BC. 【来源：21cnj*y.co*m】 【分析】分析小明同学的证明过程可知有两边对应相等的两三角形不一定全等，由此可作出判断； 利用切线的性质，可证得 OCAB，再利用等腰三角形的三线合一的性质，可证得结论。 17.【答案】 （1）解：在 Rt AOC 中，AOC60 ， ACAO sinAOC =2sin60 ， OCAB， AB2AC2 （2）解：OA= OB=2，OCAB， AOB2AOC120 . . 的长是 . 【分析】 （1）在 Rt AOC 中， 由 ACAO sinAOC，可求出 AC=

19、， 根据垂径定理可得 AB 2AC2 ； （2） 根据等腰三角形的性质可得AOB2AOC120 ，直接利用弧长公式即可求出结论. 18.【答案】 （1）解：OEAB，BAC=30 ， E 为 AB 中点，AE=， AB=2AE=， AC 为直径，半径为 1， ABC=90 ， BAC=30 ， BC=AC， OB=OC=AC OB=BC=OC， OBC 为等边三角形， OF=CF， BFOC， EF=AB= （2）解：证明：取 OB 中点 M，连接 ME，MF 【出处：21 教育名师】 OF=CF，OM=BM MF BC 由(1)可得 AE=BE，AO=OC OE BC MF OE 四边形 O

20、EM F 为平行四边形 PE=PF 延长 FM 交 AB 于点 N 则 FNBC BCBE FNBE OEBC OEFNBC EN=NB 即 FN 垂直平分 BE BF=EF BO=DO FOBD AOB=90 OA=OB BAC=45 【分析】 （1）利用垂径定理及直角三角形的性质，就看求出 AE 的长，即可求出 AB 的长，利用圆 周角定理可证得ABC=90 ，利用直角三角形的性质及等边三角形的判定，可证得 OBC 为等边 三角形，利用等边三角形的性质，然后求出 EF 的长。 （2）易证 MF 是 OBC 的中位线，利用已知易证 MF 和 BC 的数量关系和位置关系，再证明 OE 和 BC 的数量关系和位置关系，由此可证得 MF 平行且等于 OE，由此可以推出 OEMF 是平行 四边形，利用平行四边形的性质，可证得结论；延长 FM 交 AB 于点 N，利用已知易证 OEFNBC， 利用平行线分线段成比例定理可证得 EN=NB， 利用线段垂直平分线的判定和性质， 可证得 BF=EF，然后证明 AOB 是等腰直角三角形，由此可求出BAC 的度数。www.21-cn-