河北省衡水中学2020年高考数学一模试卷（文科）含答案解析

《河北省衡水中学2020年高考数学一模试卷（文科）含答案解析》由会员分享，可在线阅读，更多相关《河北省衡水中学2020年高考数学一模试卷（文科）含答案解析（30页珍藏版）》请在七七文库上搜索。

1、河北省衡水中学河北省衡水中学 2020 年年高考数学一模试卷（文科）高考数学一模试卷（文科）(解析版解析版) 一、选择题（每小题一、选择题（每小题 5 分，共分，共 60 分，下列每小题所给选项只有一项符合题意，请将正确答分，下列每小题所给选项只有一项符合题意，请将正确答 案的序号填涂在答题卡上）案的序号填涂在答题卡上） 1设集合 Mx|x2x，Nx|lgx0，则 MN（ ） A0，1 B （0，1 C0，1） D （，1 2已知，其中 x，y 是实数，i 是虚数单位，则 x+yi 的共轭复数为（ ） A1+2i B12i C2+i D2i 3已知点 M 在角 q 终边关于 yx 对称的曲线上

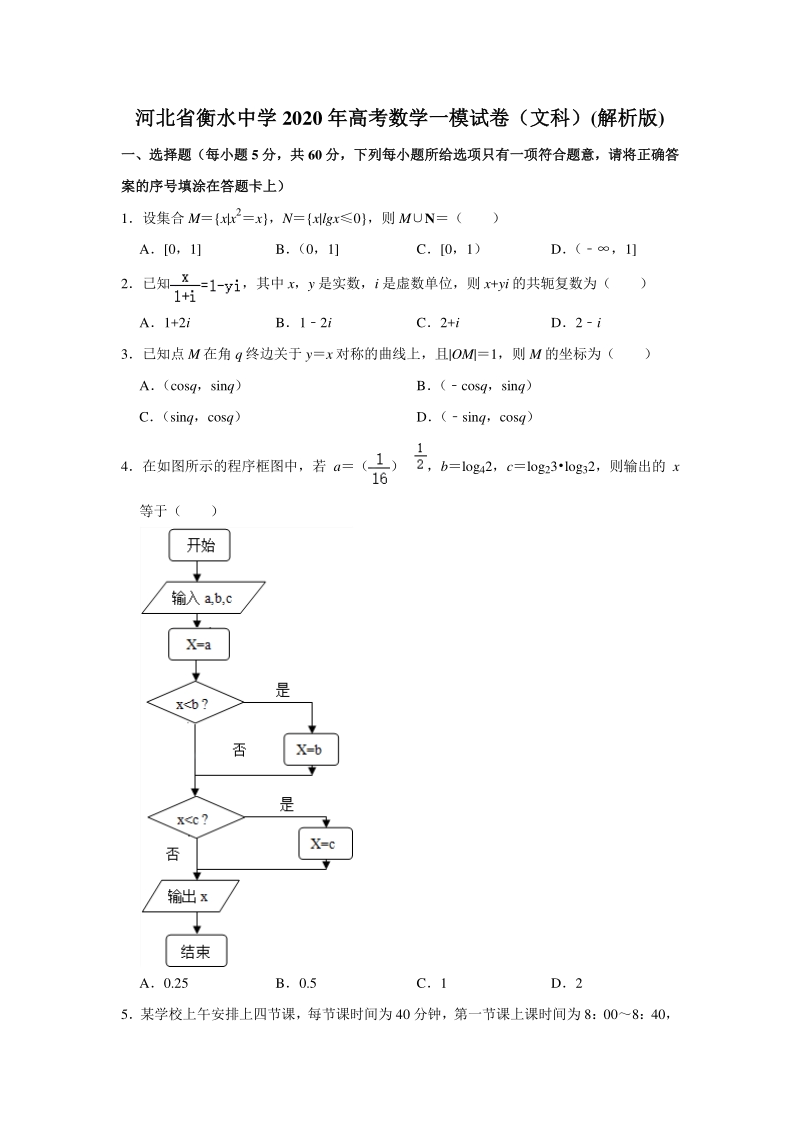
2、，且|OM|1，则 M 的坐标为（ ） A （cosq，sinq） B （cosq，sinq） C （sinq，cosq） D （sinq，cosq） 4在如图所示的程序框图中，若 a（），blog42，clog23log32，则输出的 x 等于（ ） A0.25 B0.5 C1 D2 5某学校上午安排上四节课，每节课时间为 40 分钟，第一节课上课时间为 8：008：40， 课间休息 10 分钟某学生因故迟到，若他在 9：1010：00 之间到达教室，则他听第二 节课的时间不少于 10 分钟的概率为（ ） A B C D 6设 a1，a2，anR，n3若 p：a1，a2，an成等比数列；q：

3、 （a12+a22+an12） （a22+a32+an2）（a1a2+a2a3+an1an）2，则（ ） Ap 是 q 的充分条件，但不是 q 的必要条件 Bp 是 q 的必要条件，但不是 q 的充分条件 Cp 是 q 的充分必要条件 Dp 既不是 q 的充分条件，也不是 q 的必要条件 7在某地区某高传染性病毒流行期间，为了建立指标显示校情已受控制，以便向该地区居 众显示可以过正常生活，有公共卫生专家建议的指标是“连续 7 天每天新增感染人数不 超过 5 人” ，根据连续 7 天的新增病例数计算，下列各项选项中，一定符合上述指标的是 （ ） 平均数 3； 标准差 s2； 平均数 3；且标准差

4、 s2； 平均数 3；且极差小于或等于 2； 众数等于 1 且极差小于或等于 4 A B C D 8如图，圆锥顶点为 P，底面圆心为 O，过轴 PO 的截面 PAB，C 为 PA 中点，PA4， PO6，则从点 C 经圆锥侧面到点 B 的最短距离为（ ） A2 B2 C6 D2 9小明在如图 1 所示的跑道上匀速跑步，他从点 A 出发，沿箭头方向经过点 B 跑到点 C， 共用时 30s， 他的教练选择了一个固定的位置观察小明跑步的过程， 设小明跑步的时间为 t（s） ，他与教练间的距离为 y（m） ，表示 y 与 t 的函数关系的图象大致如图 2 所示，则 这个固定位置可能是图 1 中的（ ）

5、 A点 M B点 N C点 P D点 Q 10已知抛物线 y22px（p0）的焦点为 F，准线 l 与 x 轴交于点 A，点 P 在抛物线上， 点 P 到准线 l 的距离为 d，点 O 关于准线 1 的对称点为点 B，BP 交 y 轴于点 M，若|BP| a|BM|，|OM|d则实数 a 的值是（ ） A B2 C D 11如图所示是一款热卖的小方凳，其正、侧视图如图所示，如果凳脚是由底面为正方形的 直棱柱经过切割后得到，当正方形边长为 2cm 时，则切面的面积为（ ） A B C D 12 设函数 f （x） ， 若曲线 ysinx+上存在点 （x0， y0） 使得 f （f （y0） ）

6、y0成立，则实数 a 的取值范围为（ ） A0，e2e+1 B0，e2+e1 C0，e2e1 D0，e2+e+1 二、填空题（共二、填空题（共 20 分把答案填在答题纸的横线上）分把答案填在答题纸的横线上） 13 在平面直角坐标系中， 若 x， y 满足约束条件， 则 z3x+2y 的最大值为 14某食品的保鲜时间 y（单位：小时）与储藏温度 x（单位：）满足函数关系 yekx+b （e2.718为自然对数的底数， k、 b 为常数） 若该食品在 0的保鲜时间是 192 小时， 在 22的保鲜时间是 48 小时，则该食品在 33的保鲜时间是 小时 15在平面直角坐标系 xOy 中，以 C（1，

7、1）为圆心的圆与 x 轴和 y 轴分别相切于 A，B 两 点，点 M，N 分别在线段 OA，OB 上，若 MN 与圆 C 相切，则|MN|的最小值为 16已知 O 为ABC 的外心，且 A，+2m，则 m 三、解答题（本大题共三、解答题（本大题共 5 小题，小题，1721 题每题题每题 12 分，分，22、23 选做一题选做一题 10 分，共分，共 70 分，分， 解答应写出证明过程或演算步骤，写在答题纸的相应位置）解答应写出证明过程或演算步骤，写在答题纸的相应位置） 17 （12 分）已知数列an的前 n 项和为 Sn，且 （1）若数列an+t是等比数列，求 t 的取值； （2）求数列an的

8、通项公式； （3）记，求数列bn的前 n 项和 Tn 18 （12 分）如图，四棱锥 PABCD 的底面 ABCD 为平行四边形，E，F 分别为 CD，PB 的中点 （1）求证：EF平面 PAD （2）在线段 PC 上是否存在一点 Q 使得 A，E，Q，F 四点共面？若存在，求出的值； 若不存在，请说明理由 19 （12 分）为提倡节能减排，同时减轻居民负担，广州市积极推进“一户一表”工程非 一户一表用户电费采用“合表电价”收费标准：0.65 元/度 “一户一表”用户电费采用 阶梯电价收取，其 11 月到次年 4 月起执行非夏季标准如下： 第一档 第二档 第三档 每户每月用电量（单位： 度）

9、0，200 （200，400 （400，+） 电价（单位：元/度） 0.61 0.66 0.91 例如： 某用户 11 月用电 410 度， 采用合表电价收费标准， 应交电费 4100.65266.5 元， 若采用阶梯电价收费标准，应交电费 2000.61+（400200）0.66+（410400）0.91 263.1 元 为调查阶梯电价是否能取到“减轻居民负担”的效果，随机调查了该市 100 户的 11 月用 电量，工作人员已经将 90 户的月用电量填在下面的频率分布表中，最后 10 户的月用电 量（单位：度）为：88、268、370、140、440、420、520、320、230、380

10、组别 月用电量 频数统计 频数 频率 0，100 （100，200 （200，300 （300，400 （400，500 （500，600 合计 （1）在答题卡中完成频率分布表，并绘制频率分布直方图； （2）根据已有信息，试估计全市住户 11 月的平均用电量（同一组数据用该区间的中点 值作代表） ； （3）设某用户 11 月用电量为 x 度（xN） ，按照合表电价收费标准应交 y1元，按照阶梯 电价收费标准应交 y2元，请用 x 表示 y1和 y1，并求当 y2y1时，x 的最大值，同时根据 频率分布直方图估计“阶梯电价”能否给不低于 75%的用户带来实惠？ 20 （12 分）已知椭圆 E：+

11、1（ab0）的一个焦点为 F1（，0） ，而且过点 H（，） （1）求椭圆 E 的方程； （2）设椭圆 E 的上下顶点分别为 A1，A2，P 是椭圆上异于 A1，A2的任一点，直线 PA1， PA2分别交 x 轴于点 N，M，若直线 OT 与过点 M，N 的圆 G 相切，切点为 T证明：线 段 OT 的长为定值，并求出该定值 21 （12 分）已知函数 f（x）4xx4，xR （）求 f（x）的单调区间； （） 设曲线 yf （x） 与 x 轴正半轴的交点为 P， 曲线在点 P 处的切线方程为 yg （x） ， 求证：对于任意的实数 x，都有 f（x）g（x） ； （）若方程 f（x）a（a

12、为实数）有两个实数根 x1，x2，且 x1x2，求证：x2x1 + 二选一： （本小题满分二选一： （本小题满分 10 分）请考生在分）请考生在 22、23 两题中任选一题作答，并在相应题号前的方两题中任选一题作答，并在相应题号前的方 框中涂黑框中涂黑选修选修 4-4：坐标系与参数方程：坐标系与参数方程（10 分）分） 22 （10 分）在平面直角坐标系 xoy 中，曲线 C1：（ 为参数） ，在以平面直角 坐标系的原点为极点、x 轴的正半轴为极轴，且与平面直角坐标系 xoy 取相同单位长度的 极坐标系中，曲线 C2： （1）求曲线 C1的普通方程以及曲线 C2的平面直角坐标方程； （2）若曲

13、线 C1上恰好存在三个不同的点到曲线 C2的距离相等，求这三个点的极坐标 选修选修 45：不等式选讲：不等式选讲（10 分）分） 23若 a0，b0，且 （1）求的最小值； （2）是否存在 a，b，使得的值为？并说明理由 2020 年河北省衡水中学高考数学一模试卷（文科）年河北省衡水中学高考数学一模试卷（文科） 参考答案与试题解析参考答案与试题解析 一、选择题（每小题一、选择题（每小题 5 分，共分，共 60 分，下列每小题所给选项只有一项符合题意，请将正确答分，下列每小题所给选项只有一项符合题意，请将正确答 案的序号填涂在答题卡上）案的序号填涂在答题卡上） 1设集合 Mx|x2x，Nx|lg

14、x0，则 MN（ ） A0，1 B （0，1 C0，1） D （，1 【分析】 求解一元二次方程化简 M， 求解对数不等式化简 N， 然后利用并集运算得答案 【解答】解：由 Mx|x2x0，1， Nx|lgx0（0，1， 得 MN0，1（0，10，1 故选：A 【点评】本题考查了并集及其运算，考查了对数不等式的解法，是基础题 2已知，其中 x，y 是实数，i 是虚数单位，则 x+yi 的共轭复数为（ ） A1+2i B12i C2+i D2i 【分析】由已知得出 x（1+i） （1yi） ，由复数相等的概念求出 x，y 确定出 x+yi，再得 出共轭复数 【解答】解：由已知，x（1+i） （1

15、yi） ，计算 x1+y+（1y）i 根据复数相等的概念，解得， x+yi2+i，其共轭复数为 2i 故选：D 【点评】本题考查复数的基本运算，复数相等、共轭复数的概念属于基础题 3已知点 M 在角 q 终边关于 yx 对称的曲线上，且|OM|1，则 M 的坐标为（ ） A （cosq，sinq） B （cosq，sinq） C （sinq，cosq） D （sinq，cosq） 【分析】由题意利用任意角的三角函数的定义，两点关于直线 yx 对称的特点，得出结 论 【解答】解：由题意可得点 M 的横坐标为 sinq，纵坐标为 cosq， 故选：C 【点评】本题主要考查任意角的三角函数的定义，两

16、点关于直线 yx 对称的特点，属于 基础题 4在如图所示的程序框图中，若 a（），blog42，clog23log32，则输出的 x 等于（ ） A0.25 B0.5 C1 D2 【分析】由程序框图知：算法的功能是求 a，b，c 三个数中的最大数，根据对数函数的 性质比较出 a、b、c 的大小关系即可 【解答】解：由程序框图知：算法的功能是求 a，b，c 三个数中的最大数， 由于：a（）；blog42；clog23log321， 可得：abc， 则输出 x 的值是 1 故选：C 【点评】本题考查了选择结构的程序框图，以及对数函数的性质的应用，根据框图的流 程判断算法的功能是解答此类问题的关键

17、5某学校上午安排上四节课，每节课时间为 40 分钟，第一节课上课时间为 8：008：40， 课间休息 10 分钟某学生因故迟到，若他在 9：1010：00 之间到达教室，则他听第二 节课的时间不少于 10 分钟的概率为（ ） A B C D 【分析】由题意，此学生在 9：1010：00 之间随机到达教室，区间长度为 50，他听第 二节课的时间不少于 10 分钟， 则他在 9： 109： 20 之间随机到达教室， 区间长度为 10， 即可求出概率 【解答】解：他在 9：1010：00 之间随机到达教室，区间长度为 50，他听第二节课的 时间不少于 10 分钟，则他在 9：109：20 之间随机到

18、达教室，区间长度为 10， 他在 9：1010：00 之间随机到达教室，则他听第二节课的时间不少于 10 分钟的概率 是， 故选：A 【点评】本题主要考查几何概型中的长度类型，解决的关键是找到问题的分界点，分清 是长度，面积，还是体积类型，再应用概率公式求解 6设 a1，a2，anR，n3若 p：a1，a2，an成等比数列；q： （a12+a22+an12） （a22+a32+an2）（a1a2+a2a3+an1an）2，则（ ） Ap 是 q 的充分条件，但不是 q 的必要条件 Bp 是 q 的必要条件，但不是 q 的充分条件 Cp 是 q 的充分必要条件 Dp 既不是 q 的充分条件，也不

19、是 q 的必要条件 【分析】 运用柯西不等式， 可得： （a12+a22+an12） （a22+a32+an2） （a1a2+a2a3+ +an1an）2，讨论等号成立的条件，结合等比数列的定义和充分必要条件的定义，即可得 到 【解答】解：由 a1，a2，anR，n3 运用柯西不等式，可得： （a12+a22+an12） （a22+a32+an2）（a1a2+a2a3+an1an）2， 若 a1，a2，an成等比数列，即有， 则（a12+a22+an12） （a22+a32+an2）（a1a2+a2a3+an1an）2， 即由 p 推得 q， 但由 q 推不到 p，比如 a1a2a3an0，则

20、 a1，a2，an不成等比数列 故 p 是 q 的充分不必要条件 故选：A 【点评】本题考查充分必要条件的判断，同时考查等比数列的定义，注意运用定义法和 柯西不等式解题是关键 7在某地区某高传染性病毒流行期间，为了建立指标显示校情已受控制，以便向该地区居 众显示可以过正常生活，有公共卫生专家建议的指标是“连续 7 天每天新增感染人数不 超过 5 人” ，根据连续 7 天的新增病例数计算，下列各项选项中，一定符合上述指标的是 （ ） 平均数 3； 标准差 s2； 平均数 3；且标准差 s2； 平均数 3；且极差小于或等于 2； 众数等于 1 且极差小于或等于 4 A B C D 【分析】对举反例

21、判断，对于分情况讨论，对于结合题意判断即可 【解答】解：错，举反例：0，0，0，0，2，6，6，其平均数 23，但不符合题意， 错，举反例：6，6，6，6，6，6，6，其标准差 s02，但不符合题意， 错，举反例：0，0，0，0，0，1，6，平均数 13，且标准差 s2；但不符合题意， 对，若极差小于 2，显然符合条件， 若极差小于等于 2，有可能（1）0，1，2； （2）1，2，3； （3）2，3，4； （4）3，4，5； （5）4，5，6 在平均数 3 的条件下，只有（1） （2） （3）成立，符合条件 对，在众数等于 1 且极差小于等于 4 时，最大数不超过 5，符合条件 故选：D 【点

22、评】本题考查了平均数，极差，方差等基本知识，考查分类讨论思想，是一道常规 题 8如图，圆锥顶点为 P，底面圆心为 O，过轴 PO 的截面 PAB，C 为 PA 中点，PA4， PO6，则从点 C 经圆锥侧面到点 B 的最短距离为（ ） A2 B2 C6 D2 【分析】由题意画出图形，得到圆锥沿母线剪开再展开的图形，由勾股定理求解 【解答】解：如图， 沿圆锥母线 PA 剪开再展开， PA4，PO6，OA， 则圆锥底面周长为，展开后所得扇形为半圆， B 到 B处，则从点 C 经圆锥侧面到点 B 的最短距离为 故选：A 【点评】本题考查旋转体表面上的最短距离问题，考查弧长公式的应用，是基础题 9小明

23、在如图 1 所示的跑道上匀速跑步，他从点 A 出发，沿箭头方向经过点 B 跑到点 C， 共用时 30s， 他的教练选择了一个固定的位置观察小明跑步的过程， 设小明跑步的时间为 t（s） ，他与教练间的距离为 y（m） ，表示 y 与 t 的函数关系的图象大致如图 2 所示，则 这个固定位置可能是图 1 中的（ ） A点 M B点 N C点 P D点 Q 【分析】分别假设这个位置在点 M、N、P、Q，然后结合函数图象进行判断利用排除 法即可得出答案 【解答】解：A、假设这个位置在点 M，则从 A 至 B 这段时间，y 不随时间的变化改变， 与函数图象不符，故本选项错误； B、假设这个位置在点 N

24、，则从 A 至 C 这段时间，A 点与 C 点对应 y 的大小应该相同， 与函数图象不符，故本选项错误； C、假设这个位置在点 P，则由函数图象可得，从 A 到 C 的过程中，会有一个时刻，教 练到小明的距离等于经过 30 秒时教练到小明的距离，而点 P 不符合这个条件，故本选项 错误； D、经判断点 Q 符合函数图象，故本选项正确； 故选：D 【点评】 此题考查了动点问题的函数图象， 解答本题要注意依次判断各点位置的可能性， 点 P 的位置不好排除，同学们要注意仔细观察 10已知抛物线 y22px（p0）的焦点为 F，准线 l 与 x 轴交于点 A，点 P 在抛物线上， 点 P 到准线 l

25、的距离为 d，点 O 关于准线 1 的对称点为点 B，BP 交 y 轴于点 M，若|BP| a|BM|，|OM|d则实数 a 的值是（ ） A B2 C D 【分析】由抛物线的性质可得|OF|OA|AB|，再由题意可得，进而 可得 a 的值 【解答】解：由抛物线的性质得|PF|d，因为|OM|d，|OM|PF|， 因为 B，O 关于准线对称，设准线与 x 轴的交点为 A， 所以|OF|OA|AB|， 所以，而MBOFBP 所以， 即|BP|BM|， 所以 a， 故选：D 【点评】本题考查抛物线的性质，及对应边成比例的性质，属于中档题 11如图所示是一款热卖的小方凳，其正、侧视图如图所示，如果凳

26、脚是由底面为正方形的 直棱柱经过切割后得到，当正方形边长为 2cm 时，则切面的面积为（ ） A B C D 【分析】 由正、 侧视图得当凳脚所在直线为 PC 时， 过 P 作 PA底面 ABCD， 四边形 ABCD 为正方形，设边长为 a，则PDAPBA60，设PCA，则 为 PC 与底面所 成角，推导出 sin，凳脚的切面为菱形 PMEN，PCA，由此能求出切面的面 积 【解答】解：如图 1，由正、侧视图得： 当凳脚所在直线为 PC 时，过 P 作 PA底面 ABCD， 四边形 ABCD 为正方形，设边长为 a，则PDAPBA60， 设PCA，则 为 PC 与底面所成角，PA， AC，PC

27、，sin， 如图 2，凳脚的切面为菱形 PMEN，PCA， sin， 由题意知 EC2，EP， 切面的面积为 S菱形PMEN（cm2） 故选：A 【点评】 本题考查切面面积的求法， 考查棱柱的三视图等基础知识， 考查运算求解能力， 是中档题 12 设函数 f （x） ， 若曲线 ysinx+上存在点 （x0， y0） 使得 f （f （y0） ） y0成立，则实数 a 的取值范围为（ ） A0，e2e+1 B0，e2+e1 C0，e2e1 D0，e2+e+1 【分析】利用函数 f（x）的单调性可以证明 f（y0）y0令函数 f（x）x，化为 ax2 lnxx令 h（x）x2lnxx，利用导数研

28、究其单调性即可得出 【解答】解：1sinx1， 当 sinx1 时，ysinx+取得最大值 y+e， 当 sinx1 时，ysinx+取得最小值 y+1， 即函数 ysinx+的取值范围为1，e， 若 ysinx+上存在点（x0，y0）使得 f（f（y0） ）y0成立， 则 y01，e且 f（y0）y0 若下面证明 f（y0）y0 假设 f（y0）cy0，则 f（f（y0） ）f（c）f（y0）cy0，不满足 f（f（y0） ）y0 同理假设 f（y0）cy0，则不满足 f（f（y0） ）y0 综上可得：f（y0）y0y01，e 函数 f（x），的定义域为（0，+） ， 等价为x，在（0，e上

29、有解 即平方得 lnx+x+ax2， 则 ax2lnxx， 设 h（x）x2lnxx，则 h（x）2x1， 由 h（x）0 得 1xe，此时函数单调递增， 由 h（x）0 得 0 x1，此时函数单调递减， 即当 x1 时，函数取得极小值，即 h（1）1ln110， 当 xe 时，h（e）e2lneee2e1， 则 0h（x）e2e1 则 0ae2e1 故选：C 【点评】本题考查了函数单调性的应用、利用导数研究函数的单调性，考查了推理能力 与计算能力，属于难题 二、填空题（共二、填空题（共 20 分把答案填在答题纸的横线上）分把答案填在答题纸的横线上） 13 在平面直角坐标系中， 若 x， y

30、满足约束条件， 则 z3x+2y 的最大值为 8 【分析】作出不等式组对应的平面区域，利用目标函数的几何意义，进行求最值即可 【解答】解：作出 x，y 满足约束条件对于的平面区域如图： 由 z3x+2y，则 yx+ 平移直线 yx+，由图象可知当直线 yx+， 经过点 A 时，直线 yx+的截距最大，此时 z 最大， 由，解得 A（2，1） ， 此时 zmax32+218， 故答案为：8 【点评】本题主要考查线性规划的应用，利用 z 的几何意义，利用数形结合是解决本题 的关键 14某食品的保鲜时间 y（单位：小时）与储藏温度 x（单位：）满足函数关系 yekx+b （e2.718为自然对数的底

31、数， k、 b 为常数） 若该食品在 0的保鲜时间是 192 小时， 在 22的保鲜时间是 48 小时，则该食品在 33的保鲜时间是 24 小时 【分析】由题意可得，x0 时，y192；x22 时，y48代入函数 yekx+b，解方程， 可得 k，b，再由 x33，代入即可得到结论 【解答】解：由题意可得，x0 时，y192；x22 时，y48 代入函数 yekx+b， 可得 eb192，e22k+b48， 即有 e11k，eb192， 则当 x33 时，ye33k+b19224 故答案为：24 【点评】本题考查函数的解析式的求法和运用，考查运算能力，属于中档题 15在平面直角坐标系 xOy

32、中，以 C（1，1）为圆心的圆与 x 轴和 y 轴分别相切于 A，B 两 点， 点 M， N 分别在线段 OA， OB 上， 若 MN 与圆 C 相切， 则|MN|的最小值为 22 【分析】由题意，根据圆的对称性，可得当 OCMN 时，|MN|取最小值 【解答】解：在平面直角坐标系 xOy 中，以 C（1，1）为圆心的圆与 x 轴和 y 轴分别 相切于 A，B 两点， 点 M，N 分别在线段 OA，OB 上，MN 与圆 C 相切， 根据圆的对称性，当 OCMN 时，|MN|取最小值， 如图，|OC|， |MN|的最小值为 2（）22 故答案为：22 【点评】本题考查线段长的最小值的求法，考查直

33、线、圆等基础知识，考查运算求解能 力，考查函数与方程思想，是中档题 16已知 O 为ABC 的外心，且 A，+2m，则 m 【分析】先将等式左右两边同时乘以，得：+2m 2，再 利用由正弦定理得：sinCcosB+cosCsinBm 然后利用两角的和差公式求解 【解答】解：+2m 等式两边同时乘 得：+2m 2 又 2AO 2+24 m 由正弦定理得： + 又 AsinA sinCcosB+cosCsinBm msin（B+C）sinA 故应填 【点评】本题考查了向量的数量积，正弦定理及两角的和差公式，属难度较大的题 三、解答题（本大题共三、解答题（本大题共 5 小题，小题，1721 题每题题

34、每题 12 分，分，22、23 选做一题选做一题 10 分，共分，共 70 分，分， 解答应写出证明过程或演算步骤，写在答题纸的相应位置）解答应写出证明过程或演算步骤，写在答题纸的相应位置） 17 （12 分）已知数列an的前 n 项和为 Sn，且 （1）若数列an+t是等比数列，求 t 的取值； （2）求数列an的通项公式； （3）记，求数列bn的前 n 项和 Tn 【分析】 （1）直接利用数列的等比中项求出 t 的值 （2）利用等比数列的定义求出数列的通项公式 （3）利用裂项相消法求出数列的和 【解答】解： （1）由，得 a11， 当 n1 时，anSnSn12ann2an1+（n1） ，

35、即 an2an1+1， 所以 a23，a37， 依题意， （3+t）2（1+t）（7+t） ， 解得 t1 （2）有（2）知 an2an1+1， 所以 an+12（an1+1） ，又因为 a1+12， 所以数列an+1是以 2 为首项，2 为公比的等比数列， 所以， 所以 （3）由（2）知， 则 【点评】本题考查的知识要点：数列的通项公式的应用及数列的通项公式的求法，裂项 相消法在数列求和中的应用 18 （12 分）如图，四棱锥 PABCD 的底面 ABCD 为平行四边形，E，F 分别为 CD，PB 的中点 （1）求证：EF平面 PAD （2）在线段 PC 上是否存在一点 Q 使得 A，E，Q

36、，F 四点共面？若存在，求出的值； 若不存在，请说明理由 【分析】 （1）取 PA 的中点 M，连接 MD，MF，证明四边形 DEFM 为平行四边形，可得 EFDM，由直线与平面平行的判定可得 EF平面 PAD； （2）取 AB 的中点 H，连接 PH 交 AF 于 G，在 PC 上取点 Q，使 PQ：QC2：1，连接 GQ，HC，则 A，E，Q，F 四点共面，然后证明即可 【解答】解： （1）证明：如图，取 PA 的中点 M，连接 MD，MF， F，M 分别为 PB，PA 的中点，FMAB，FMAB， 又四边形 ABCD 是平行四边形，ABCD，ABCD， E 为 CD 的中点，DEAB，D

37、EAB DEFM，DEFM，则四边形 DEFM 为平行四边形， EFDM EF平面 PAD，DM平面 PAD， EF平面 PAD； （2）存在点 Q 符合题目条件，且此时 PQ：QC2：1 取 AB 的中点 H，连接 PH 交 AF 于 G，在 PC 上取点 Q，使 PQ：QC2：1， 连接 GQ，HC，则 A，E，Q，F 四点共面 证明如下：在平行四边形 ABCD 中，E，H 分别为 CD，AB 的中点， CHAE，又 F 是 PB 的中点， G 是PAB 的重心，且 PG：GH2：1 又 PQ：QC2：1，GQHC， CHAE，GQAE， GQ 与 AE 确定一个平面 ，而 F直线 AG，

38、 F，则 A，E，Q，F 四点共面 故在线段 PC 上存在一点 Q，使得 A，E，Q，F 四点共面 【点评】本题考查直线与平面平行的判定，平面的基本性质，考查空间想象能力与思维 能力，是中档题 19 （12 分）为提倡节能减排，同时减轻居民负担，广州市积极推进“一户一表”工程非 一户一表用户电费采用“合表电价”收费标准：0.65 元/度 “一户一表”用户电费采用 阶梯电价收取，其 11 月到次年 4 月起执行非夏季标准如下： 第一档 第二档 第三档 每户每月用电量（单位： 度） 0，200 （200，400 （400，+） 电价（单位：元/度） 0.61 0.66 0.91 例如： 某用户 1

39、1 月用电 410 度， 采用合表电价收费标准， 应交电费 4100.65266.5 元， 若采用阶梯电价收费标准，应交电费 2000.61+（400200）0.66+（410400）0.91 263.1 元 为调查阶梯电价是否能取到“减轻居民负担”的效果，随机调查了该市 100 户的 11 月用 电量，工作人员已经将 90 户的月用电量填在下面的频率分布表中，最后 10 户的月用电 量（单位：度）为：88、268、370、140、440、420、520、320、230、380 组别 月用电量 频数统计 频数 频率 0，100 （100，200 （200，300 （300，400 （400，5

40、00 （500，600 合计 （1）在答题卡中完成频率分布表，并绘制频率分布直方图； （2）根据已有信息，试估计全市住户 11 月的平均用电量（同一组数据用该区间的中点 值作代表） ； （3）设某用户 11 月用电量为 x 度（xN） ，按照合表电价收费标准应交 y1元，按照阶梯 电价收费标准应交 y2元，请用 x 表示 y1和 y1，并求当 y2y1时，x 的最大值，同时根据 频率分布直方图估计“阶梯电价”能否给不低于 75%的用户带来实惠？ 【分析】 （1）完成频率分布表，作出频率分布直方图 （2）由频率分布直方图能求出该 100 户用户 11 月的平均用电量，由此能估计全市住户 11 月

41、的平均用电量 （3） 求出 y10.65x， y2， 由 y2y1， 解得 x423.1，从而 x 的最大值为 423根据频率分布直方图，能估计“阶梯电 价”能给不低于 75%的用户带来实惠 【解答】解： （1）频率分布表如下： 组别 月用电量 频数 频率 0，100 4 0.04 （100，200 12 0.12 （200，300 24 0.24 （300，400 30 0.3 （400，500 26 0.26 （500，600 4 0.04 合计 100 1 频率分布直方图如下： （2）该 100 户用户 11 月的平均用电量： 度 所以估计全市住户 11 月的平均用电量为 324 度 （

42、3）y10.65x， y2， 由 y2y1，得或或， 解得 x423.1， xN，x 的最大值为 423 根据频率分布直方图，x423 时的频率为： 0.04+0.12+0.24+0.3+230.260.75980.75， 故估计“阶梯电价”能给不低于 75%的用户带来实惠 【点评】本题考查频率分布表、频率分布直方图的应用，考查平均数、概率的求法，考 查运算求解能力，考查数形结合思想，是中档题 20 （12 分）已知椭圆 E：+1（ab0）的一个焦点为 F1（，0） ，而且过点 H（，） （1）求椭圆 E 的方程； （2）设椭圆 E 的上下顶点分别为 A1，A2，P 是椭圆上异于 A1，A2的

43、任一点，直线 PA1， PA2分别交 x 轴于点 N，M，若直线 OT 与过点 M，N 的圆 G 相切，切点为 T证明：线 段 OT 的长为定值，并求出该定值 【分析】（） 解法一： 根据椭圆 E：的一个交点为， 过点，可得 a2b23，联立即可求得椭圆 E 的方程； 解法二：椭圆的两个焦点分别为，利用椭圆的定义，可求 椭圆 E 的方程； （）解法一：由（）可知 A1（0，1） ，A2（0，1） ，设 P（x0，y0） ，求出， 同 设圆G的圆心为，利用 ，即可 得到线段 OT 的长度； 解法二： 由 （） 可知 A1（0， 1） ， A2（0， 1） ， 设 P （x0， y0） ， 求出，

44、 可得，由切割线定理可得线段 OT 的长度 【解答】 （）解法一：由题意，椭圆 E：的一个交点为 ， a2b23， 椭圆过点 ， 解得 a24，b21， 所以椭圆 E 的方程为（4 分） 解法二：椭圆的两个焦点分别为， 由椭圆的定义可得，所以 a2，b21， 所以椭圆 E 的方程为（4 分） （）解法一：由（）可知 A1（0，1） ，A2（0，1） ，设 P（x0，y0） ， 直线 PA1：，令 y0，得； 直线 PA2：，令 y0，得； 设圆 G 的圆心为， 则 r2， ， 而，所以，所以， 所以|OT|2，即线段 OT 的长度为定值 2（14 分） 解法二：由（）可知 A1（0，1） ，A

45、2（0，1） ，设 P（x0，y0） ， 直线 PA1：，令 y0，得； 直线 PA2：，令 y0，得； 则，而，所以， 所以，由切割线定理得 OT2|OM|ON|4 所以|OT|2，即线段 OT 的长度为定值 2（14 分） 【点评】本题考查椭圆的标准方程，考查圆与椭圆为综合，考查线段长的求解，认真审 题，挖掘隐含是关键 21 （12 分）已知函数 f（x）4xx4，xR （）求 f（x）的单调区间； （） 设曲线 yf （x） 与 x 轴正半轴的交点为 P， 曲线在点 P 处的切线方程为 yg （x） ， 求证：对于任意的实数 x，都有 f（x）g（x） ； （）若方程 f（x）a（a 为

46、实数）有两个实数根 x1，x2，且 x1x2，求证：x2x1 + 【分析】 （）求出原函数的导函数，得到导函数的零点，由零点对定义域分段，根据导 函数在各区间段内的符号得到原函数的单调性； （）设出点 p 的坐标，利用导数求出切线方程 g（x）f（x0） （xx0） ，构造辅助函 数 F（x）f（x）g（x） ，利用导数得到对于任意实数 x， 有 F（x）F（x0）0，即对任意实数 x，都有 f（x）g（x） ； （）由（）知，求出方程 g（x）a 的根， 由 g（x）在（，+）上单调递减，得到 x2x2 同理得到 x1x1，则可证得 【解答】 （）解：由 f（x）4xx4，可得 f（x）44

47、x3 当 f（x）0，即 x1 时，函数 f（x）单调递增； 当 f（x）0，即 x1 时，函数 f（x）单调递减 f（x）的单调递增区间为（，1） ，单调递减区间为（1，+） （）证明：设点 p 的坐标为（x0，0） ，则，f（x0）12， 曲线 yf（x）在点 P 处的切线方程为 yf（x0） （xx0） ，即 g（x）f（x0） （x x0） ， 令函数 F（x）f（x）g（x） ，即 F（x）f（x）f（x0） （xx0） ， 则 F（x）f（x）f（x0） F（x0）0，当 x（，x0）时，F（x）0；当 x（x0，+）时，F（x） 0， F（x）在（，x0）上单调递增，在（x0，+

48、）上单调递减， 对于任意实数 x，F（x）F（x0）0，即对任意实数 x，都有 f（x）g（x） ； （）证明：由（）知，设方程 g（x）a 的根为 x2，可得 g（x）在（，+）上单调递减，又由（）知 g（x2）f（x2）ag（x2） ， 因此 x2x2 类似地，设曲线 yf（x）在原点处的切线方程为 yh（x） ，可得 h（x）4x， 对于任意的 x（，+） ，有 f（x）h（x）x40，即 f（x）h（x） 设方程 h（x）a 的根为 x1，可得， h（x）4x 在（，+）上单调递增，且 h（x1）af（x1）h（x1） ， 因此 x1x1， 由此可得 【点评】本小题主要考查导数的运算、导