 考点24 解直角三角形备战2020年中考数学一轮复习考点导练案
考点24 解直角三角形备战2020年中考数学一轮复习考点导练案
《考点24 解直角三角形备战2020年中考数学一轮复习考点导练案》由会员分享,可在线阅读,更多相关《考点24 解直角三角形备战2020年中考数学一轮复习考点导练案(28页珍藏版)》请在七七文库上搜索。
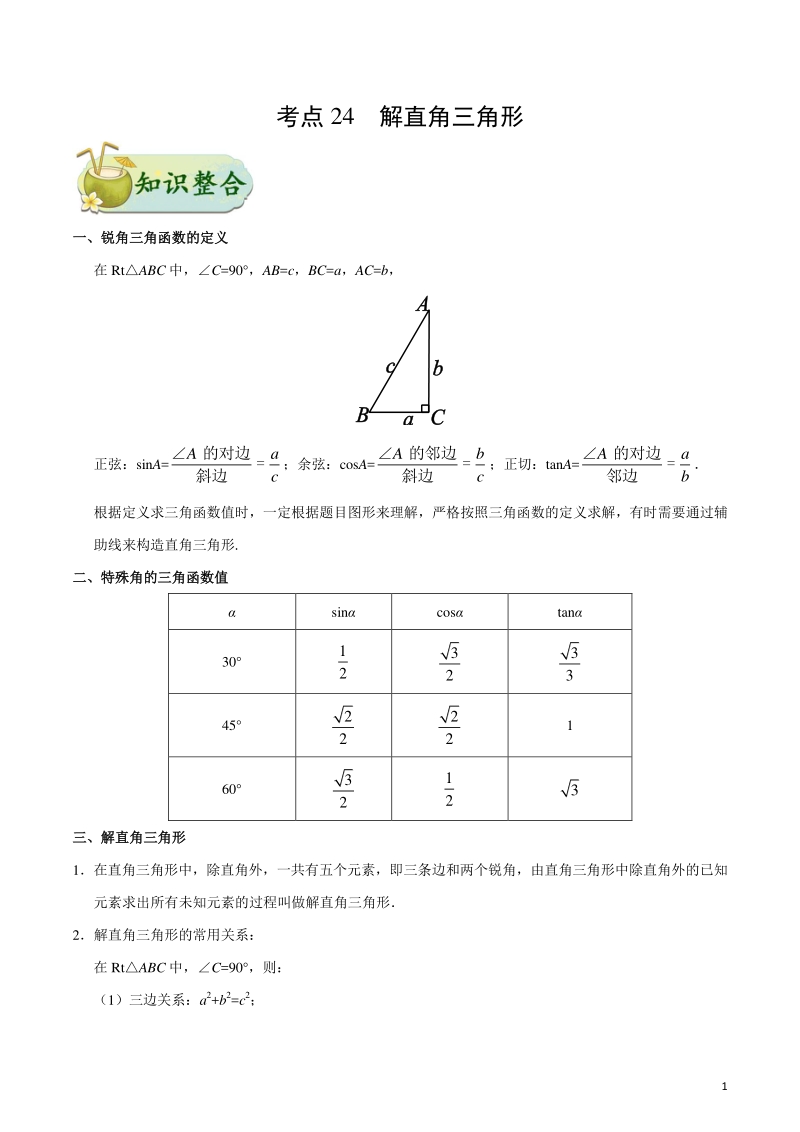
1、 1 考点 24 解直角三角形 一、一、锐角三角函数的定义锐角三角函数的定义 在 RtABC 中,C=90 ,AB=c,BC=a,AC=b, 正弦:sinA= 的对边 = 斜边 Aa c ;余弦:cosA= 的邻边 = 斜边 Ab c ;正切:tanA= 的对边 = 邻边 Aa b 根据定义求三角函数值时,一定根据题目图形来理解,严格按照三角函数的定义求解,有时需要通过辅 助线来构造直角三角形. 二、二、特殊角的三角函数值特殊角的三角函数值 sin cos tan 30 1 2 3 2 3 3 45 2 2 2 2 1 60 3 2 1 2 3 三、三、解直角三角形解直角三角形 1在直角三角形
2、中,除直角外,一共有五个元素,即三条边和两个锐角,由直角三角形中除直角外的已知 元素求出所有未知元素的过程叫做解直角三角形 2解直角三角形的常用关系: 在 RtABC 中,C=90 ,则: (1)三边关系:a2+b2=c2; 2 (2)两锐角关系:A+B=90 ; (3)边与角关系:sinA=cosB= a c ,cosA=sinB= b c ,tanA= a b ; (4)sin2A+cos2A=1 3科学选择解直角三角形的方法口诀: 已知斜边求直边,正弦、余弦很方便; 已知直边求直边,理所当然用正切; 已知两边求一边,勾股定理最方便; 已知两边求一角,函数关系要记牢; 已知锐角求锐角,互余
3、关系不能少; 已知直边求斜边,用除还需正余弦. 四、四、解直角三角形的应用解直角三角形的应用 1仰角和俯角 仰角:在视线与水平线所成的角中,视线在水平线上方的角叫做仰角 俯角:在视线与水平线所成的角中,视线在水平线下方的角叫做俯角 2坡度和坡角 坡度:坡面的铅直高度 h 和水平宽度 l 的比叫做坡面的坡度(或坡比) ,记作 i= h l 坡角:坡面与水平面的夹角叫做坡角,记作 ,i=tan 坡度越大, 角越大,坡面越陡 3方向角(或方位角) 指北或指南方向线与目标方向线所成的小于 90 的水平角叫做方向角 4解直角三角形中“双直角三角形”的基本模型: 3 解题方法:这两种模型种都有一条公共的直
4、角边,解题时,往往通过这条边为中介在两个三角形中依次 求边,或通过公共边相等,列方程求解. 5解直角三角形实际应用的一般步骤 (1)弄清题中名词、术语,根据题意画出图形,建立数学模型; (2)将条件转化为几何图形中的边、角或它们之间的关系,把实际问题转化为解直角三角形问题; (3)选择合适的边角关系式,使运算简便、准确; (4)得出数学问题的答案并检验答案是否符合实际意义,从而得到问题的解 考向一 求三角函数的值 (1)分清直角三角形中的斜边与直角边. (2)正确地表示出直角三角形的三边长,常设某条直角边长为 k(有时也可设为 1) ,在求三角函数值的过 程中约去 k (3)正确应用勾股定理求
5、第三边长 (4)应用锐角三角函数定义,求出三角函数值 典例典例 1 2sin45的值为 A 2 2 B 3 C 2 D1 【答案】C 【解析】把 sin45 = 2 2 代入原式得:原式=2 2 2 = 2故选 C 4 1如图,在ABC 中,C=90若 AB=3,BC=2,则 sinA 的值为 A 2 3 B 5 3 C 2 5 5 D 5 2 考向二 利用特殊角的三角函数值求值 锐角三角函数值与三角形三边的长短无关,只与锐角的大小有关. 典例典例 2 已知A 为锐角,且 sinA= 3 2 ,那么A 等于 A15 B30 C45 D60 【答案】D 【解析】sinA= 3 2 ,A=60故选
6、 D 2已知 是锐角,sin=cos60,则 等于 A30 B45 C60 D不能确定 考向三 解直角三角形的应用 解此类题的一般方法: (1)构造直角三角形; (2)理清直角三角形的边角关系; (3)利用特殊角的三角函 数值解答问题. 5 典例典例 3 某山的山顶 B 处有一个观光塔,已知该山的山坡面与水平面的夹角BDC 为 30 ,山高 BC 为 100 米,点 E 距山脚 D 处 150 米,在点 E 处测得观光塔顶端 A 的仰角为 60 ,则观光塔 AB 的高度是 A50 米 B100 米 C125 米 D150 米 【答案】A 【解析】如图,作 EFAC 于 F,EGDC 于 G,在
7、 RtDEG 中,EG= 1 2 DE=75, BF=BC-CF=BC-CE=100-75=25,EF= tantan30 BFBF BEF =25 3, AEF=60 , A=30 , AF= 25 3 tan3 3 EF A =75, AB=AF-BF=50(米),故观光塔 AB 的高度为 50 米, 故选 A 3如图,某湖心岛上有一亭子A,在亭子A的正东方向上的湖边有一棵树B,在这个湖心岛的湖边C处 测得亭子A在北偏西45方向上, 测得树B在北偏东36方向上, 又测得B、C之间的距离等于200米, 求A、B之间的距离(结果精确到1米) 6 (参考数据: 21.414 ,sin360.58
8、8,cos360.809,tan360.727,cot361.376) 1如图,在ABC 中,若C=90,则 AsinA= a c BsinA= b c CcosA= a b DcosA= b a 2计算 1 2 sin45cos60 2 的值为 A 1 13 2 B 1 13 2 C 1 4 D 3 4 3在RtABC中,90C, 53B ,若BCm,则AB的长为 A cos53 m Bcos53m Csin53m Dtan53m 4在 RtABC 中,C=90 , 1 3 ACAB,则 cosA 等于 7 A 2 2 3 B 1 3 C2 2 D 2 4 5菱形 ABCD 的对角线 AC=
9、10cm,BD=6cm,那么 tan 2 B 为 A 5 3 B 5 4 C 5 34 D 3 34 6如图是边长为 1 的小正方形组成的网格图,其中点 A,B,C 均为格点,则 sinBAC 为 A 2 2 B 5 5 C 10 5 D 10 10 7在 RtABC 中,C=90 ,若 AB=10,sinA= 3 5 ,则斜边上的高等于 A5 B4.8 C4.6 D4 8如图,在边长为 1 的小正方形组成的网格中,ABC 的三个顶点均在格点上,则 tanABC 的值为 A 3 5 B 3 4 C 10 5 D1 9如图,某水库堤坝横截面迎水坡AB的坡度是1:3,堤坝高为40m,则迎水坡面的是
10、 A80m B 80 3m C 40m D 40 3m 10如图,一艘海轮位于灯塔 P 的北偏东 55 方向,距离灯塔为 2 海里的点 A 处如果海轮沿正南方向航行 到灯塔的正东位置 B 处,海轮航行的距离 AB 长是 8 A2 海里 B2sin55海里 C2cos55海里 D2tan55海里 11钓鱼是一项特别锻炼心性的运动,如图,小南在江边垂钓,河堤 AB 的坡度为 12.4,AB 长为 3.9 米, 钓竿 AC 与水平线的夹角是 60 ,其长为 4.5 米,若钓竿 AC 与钓鱼线 CD 的夹角也是 60 ,则浮漂 D 与 河堤下端 B 之间的距离约为(参考数据:31.732) A1.73
11、2 米 B1.754 米 C1.766 米 D1.823 米 12如图,在 RtABC 中,C=90 ,BC=12,tanA= 12 5 ,则 sinB=_ 13在ABC 中,AB=2 5,AC=5,tanB= 1 2 ,则 BC 的长度为_ 14已知相邻的两根电线杆AB与CD高度相同,且相距50mBC 小王为测量电线杆的高度,在两根 电线杆之间某一处E架起测角仪,如图所示,分别测得两根电线杆顶端的仰角为45、23,已知测 角仪EF高1.5m,则电线杆的高度约为_m (精确到0.1m,参考数据:sin230.39, cos230.92,tan230.43) 9 15已知:如图,在菱形 ABCD
12、 中,AEBC,垂足为 E,对角线 BD=8,tanCBD= 1 2 (1)求边 AB 的长; (2)求 cosBAE 的值 16如图是小强洗漱时的侧面示意图,洗漱台(矩形 ABCD)靠墙摆放,高 AD=80cm,宽 AB=48cm,小强的 身高为 166cm,其中下半身 FG=100cm,洗漱时下半身与地面成 80 角(FGK=80 ),身体前倾成 125 角(EFG=125 ),脚与洗漱台的距离 GC=15cm(点 D,C,G,K 在同一直线上) (1)此时小强的头部点 E 与地面 DK 的距离是多少? (2)小强希望他的头部 E 恰好在洗漱盆 AB 的中点 O 的正上方,他应向前或后退多
13、少? (sin800.98,cos800.17,21.41,结果精确到 0.1cm) 10 1(2019天津)60sin2的值等于 A1 B 2 C3 D2 2(2019怀化)已知 为锐角,且 sin= 1 2 ,则= A30 B45 C60 D90 3(2019宜昌)如图,在 5 4 的正方形网格中,每个小正方形的边长都是 1,ABC 的顶点都在这些小 正方形的顶点上,则 sinBAC 的值为 A 4 3 B 3 4 C 3 5 D 4 5 4(2019广州)如图,有一斜坡 AB,坡顶 B 离地面的高度 BC 为 30 m,斜坡的倾斜角是BAC,若 tanBAC= 2 5 ,则此斜坡的水平距
14、离 AC 为 A75 m B50 m C30 m D12 m 5(2019苏州)如图,小亮为了测量校园里教学楼AB的高度,将测角仪CD竖直放置在与教学楼水平距 离为18 3m的地面上,若测角仪的高度为1.5 m,测得教学楼的顶部A处的仰角为30o,则教学楼的高 度是 11 30 C D A B A55.5m B54m C19.5m D18m 6(2019广西)小菁同学在数学实践活动课中测量路灯的高度如图,已知她的目高 AB 为 1.5 米,她先 站在 A 处看路灯顶端 O 的仰角为 35,再往前走 3 米站在 C 处,看路灯顶端 O 的仰角为 65,则路灯 顶端 O 到地面的距离约为(已知 s
15、in350.6,cos350.8,tan350.7,sin650.9,cos65 0.4,tan652.1) A3.2 米 B3.9 米 C4.7 米 D5.4 米 7 (2019杭州)如图,一块矩形木板 ABCD 斜靠在墙边(OCOB,点 A,B,C,D,O 在同一平面内), 已知 AB=a,AD=b,BCO=x,则点 A 到 OC 的距离等于 Aasinx+bsinx Bacosx+bcosx Casinx+bcosx Dacosx+bsinx 8(2019甘肃)在ABC 中,C=90,tanA= 3 3 ,则 cosB=_ 9(2019杭州)在直角三角形 ABC 中,若 2AB=AC,则
16、 cosC=_ 10(2019天津)如图,海面上一艘船由西向东航行,在 A 处测得正东方向上一座灯塔的最高点 C 的仰角 为 31,再向东继续航行 30m 到达 B 处,测得该灯塔的最高点 C 的仰角为 45,根据测得的数据, 12 计算这座灯塔的高度 CD(结果取整数)参考数据:sin310.52,cos310.86,tan310.60 11(2019深圳)如图所示,某施工队要测量隧道长度 BC,AD=600 米,ADBC,施工队站在点 D 处看 向 B,测得仰角为 45,再由 D 走到 E 处测量,DEAC,ED=500 米,测得仰角为 53,求隧道 BC 长(sin53 4 5 ,cos
17、53 3 5 ,tan53 4 3 ) 13 12(2019河南)数学兴趣小组到黄河风景名胜区测量炎帝塑像(塑像中高者)的高度如图所示,炎帝 塑像 DE 在高 55m 的小山 EC 上,在 A 处测得塑像底部 E 的仰角为 34,再沿 AC 方向前进 21m 到达 B 处,测得塑像顶部 D 的仰角为 60,求炎帝塑像 DE 的高度 (精确到 1m参考数据:sin340.56,cos34=0.83,tan340.67,31.73) 13(2019甘肃)为了保证人们上下楼的安全,楼梯踏步的宽度和高度都要加以限制中小学楼梯宽度的 范围是 260mm300mm 含(300mm),高度的范围是 120m
18、m150mm(含 150mm)如图是某中学 的楼梯扶手的截面示意图, 测量结果如下: AB, CD 分别垂直平分踏步 EF, GH, 各踏步互相平行, AB=CD, AC=900mm,ACD=65,试问该中学楼梯踏步的宽度和高度是否符合规定(结果精确到 1mm,参 考数据:sin650.906,cos650.423) 14 14(2019江西)图 1 是一台实物投影仪,图 2 是它的示意图,折线 BAO 表示固定支架,AO 垂直水 平桌面 OE 于点 O,点 B 为旋转点,BC 可转动,当 BC 绕点 B 顺时针旋转时,投影探头 CD 始终垂直 于水平桌面 OE,经测量:AO=6.8cm,CD


- 配套讲稿:
如PPT文件的首页显示word图标,表示该PPT已包含配套word讲稿。双击word图标可打开word文档。
- 特殊限制:
部分文档作品中含有的国旗、国徽等图片,仅作为作品整体效果示例展示,禁止商用。设计者仅对作品中独创性部分享有著作权。
- 关 键 词:
- 考点24 解直角三角形 备战2020年中考数学一轮复习考点导练案 考点 24 直角三角形 备战 2020 年中 数学 一轮 复习 导练案
 七七文库所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
七七文库所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。



 浙公网安备33030202001339号
浙公网安备33030202001339号
链接地址:https://www.77wenku.com/p-164984.html