2020年中考数学第一轮复习知识点20二次函数几何方面的应用

《2020年中考数学第一轮复习知识点20二次函数几何方面的应用》由会员分享，可在线阅读，更多相关《2020年中考数学第一轮复习知识点20二次函数几何方面的应用（155页珍藏版）》请在七七文库上搜索。

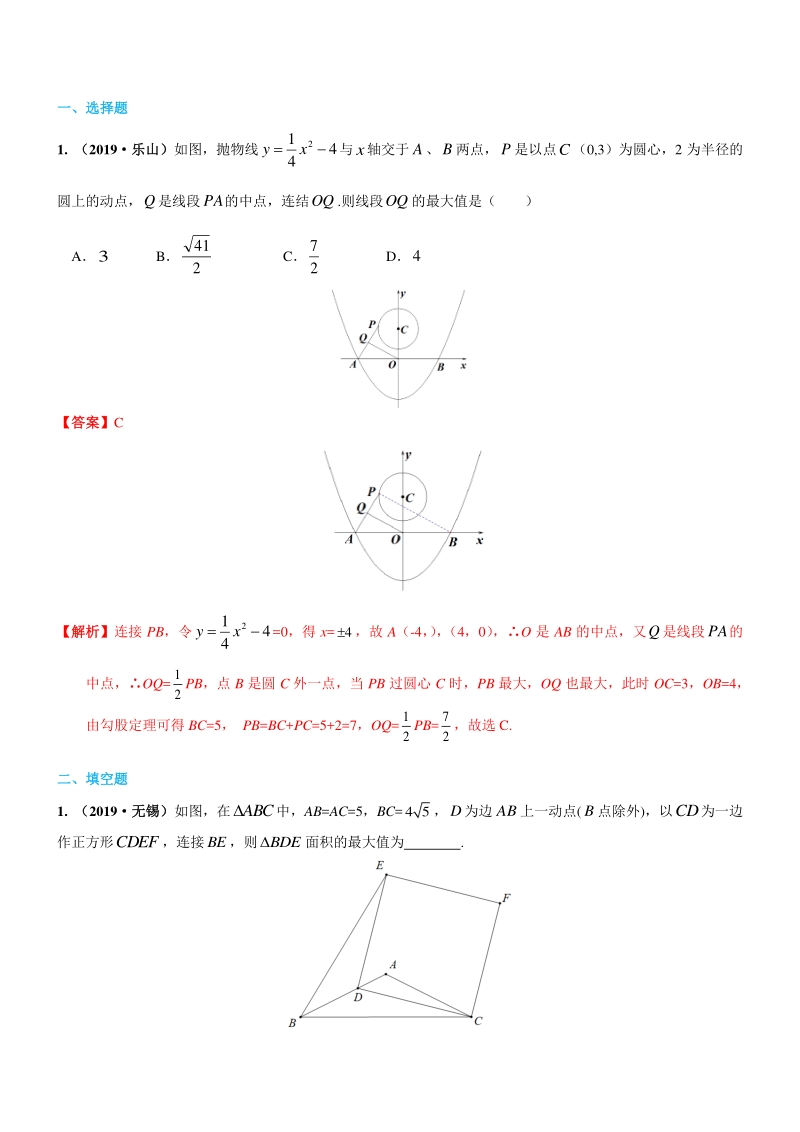
1、 一、选择题一、选择题 1. （2019乐山）乐山）如图，抛物线4 4 1 2 xy与x轴交于A、B两点，P是以点C（0,3）为圆心，2 为半径的 圆上的动点，Q是线段PA的中点，连结OQ.则线段OQ的最大值是（ ） A3 B 2 41 C 2 7 D4 【答案】【答案】C 【解【解析析】连接 PB，令4 4 1 2 xy=0，得 x=4，故 A（-4， ） ， （4，0） ，O 是 AB 的中点，又Q是线段PA的 中点，OQ= 1 2 PB，点 B 是圆 C 外一点，当 PB 过圆心 C 时，PB 最大，OQ 也最大，此时 OC=3，OB=4， 由勾股定理可得 BC=5， PB=BC+PC=

2、5+2=7，OQ= 1 2 PB= 7 2 ，故选 C. 二、填空题二、填空题 1. （2019无锡）无锡）如图，在ABC中，AB=AC=5，BC=4 5，D为边AB上一动点(B点除外)，以CD为一边 作正方形CDEF，连接BE，则BDE面积的最大值为 . 【答案】8 【解【解析析】过 D 作 DGBC 于 G，过 A 作 ANBC 于 N，过 E 作 EHHG 于 H，延长 ED 交 BC 于 M.易证EHD DGC，可设 DG=HE=x，AB=AC=5，BC=4 5，ANBC，BN= 1 2 BC=25，AN= 22 5ABBN， GBC，ANBC，DGAN，2 BGBN DGAN ，BG

3、=2x，CG=HD=45- 2x；易证HEDGMD，于 是 HEHD GMGD ， 4 52xx GMx ，即 MG 2 4 52 x x ，所以 SBDE = 1 2 BMHD= 1 2 （2x 2 4 52 x x ）（4 5- 2x）= 2 5 4 5 2 xx= 2 54 5 8 25 x ，当 x= 4 5 5 时，SBDE的最大值为 8. 2. (2019 台州台州)如图,直线 l1l2l3,A,B,C 分别为直线 l1,l2,l3上的动点,连接 AB,BC,AC,线段 AC 交直线 l2于点 D. 设直线 l1,l2之间的距离为 m,直线 l2,l3之间的距离为 n,若ABC90

4、,BD4,且 2 3 m n ,则 m+n 的最大值为 _. 【答案】【答案】 25 3 【解【解析析】 过点 B 作 BEl1于点 E,作 BFl3于点 F,过点 A 作 ANl2于点 N,过点 C 作 CMl2于点 M,设 AEx,CF y,则 BNx,BMy,BD4,DMy4,DN4x,ABC90,且AEBBFC90,CMD AND 90 ,易 得AEB BFC, CMD AND, AEBE BFCF , 即 xm ny ,mn xy, ANDN CMDM , 即 42 = 43 mx ny ,y10 3 2 x, 2 = 3 m n ,n 3 2 m,m+n 5 2 m,mnxyx(1

5、0 3 2 x) 3 2 x2+10 x 3 2 m2,当 x 10 3 时,mn 取得最大值为 50 3 , 3 2 m2 50 3 ,m最大 10 3 ,m+n 5 2 m 25 3 . 3. （2019凉山凉山）如图，正方形 ABCD 中，AB=12, AE = 4 1 AB，点 P 在 BC 上运动 （不与 B、C 重合） ，过点 P 作 PQEP，交 CD 于点 Q，则 CQ 的最大值为 . 【答案】4 【解析】在正方形 ABCD 中，AB=12, AE = 4 1 AB=3，BC=AB=12，BE=9，设 BP=x，则 CP=12-x.PQEP， EPQ=B=C=90，BEP+BP

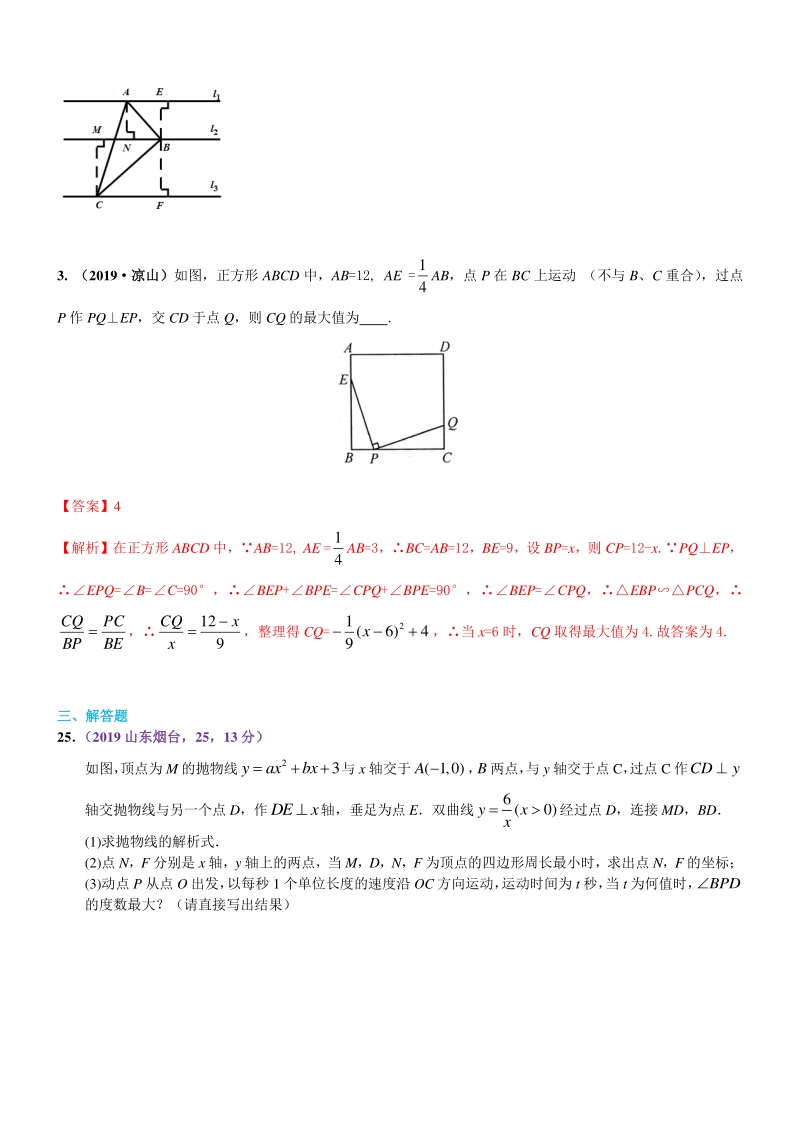
6、E=CPQ+BPE=90，BEP=CPQ，EBPPCQ， BE PC BP CQ ， 9 12x x CQ ，整理得 CQ=4)6( 9 1 2 x，当 x=6 时，CQ 取得最大值为 4.故答案为 4. 三、解答题三、解答题 25 （2019 山东烟台，山东烟台，25，13 分）分） 如图， 顶点为 M 的抛物线 2 3yaxbx与 x 轴交于( 1,0)A ，B两点， 与 y 轴交于点 C， 过点 C 作CDy 轴交抛物线与另一个点 D，作DEx轴，垂足为点 E双曲线 6 (0)yx x 经过点 D，连接 MD，BD (1)求抛物线的解析式 (2)点 N，F 分别是 x 轴，y 轴上的两点

7、，当 M，D，N，F 为顶点的四边形周长最小时，求出点 N，F 的坐标； (3)动点 P 从点 O 出发， 以每秒 1 个单位长度的速度沿 OC 方向运动， 运动时间为 t 秒， 当 t 为何值时，BPD 的度数最大？（请直接写出结果） 【解题过程】【解题过程】 （1）当）当0 x时时 2 0033yab 所以所以3OC ，( 0 , 3)C， 因为因为CDy轴，DEx轴，COEO， 所以四边形所以四边形 OEDC 为矩形，为矩形， 又因为双曲线又因为双曲线 6 (0 )yx x 经过点经过点 D， 所以所以6 OEDC S 矩形 , 所以所以2 O E D C S CD OC 矩形 , 所以

8、所以( 2, 3)D 将点将点( 1, 0 )A 、( 2, 3)D代入抛物线代入抛物线 2 3ya xb x得得 30 4233 ab ab 解得解得 1 2 a b 所以抛物线的表达式为所以抛物线的表达式为 2 23yxx （2）解：）解：作点作点 D 关于关于 x 轴的对称点轴的对称点H，作点，作点 M 关于关于 y 轴的对称点轴的对称点I，如图（，如图（1） 由图形轴对称的性质可知由图形轴对称的性质可知FMFI，NDNH， 所以四边形所以四边形 MDNF 的周长的周长MDDNFNFMMDNHFNFI， 因为因为MD是定值，所以当是定值，所以当NHFNFI最小时，四边形最小时，四边形 M

9、DNF 的周长最小，的周长最小， 因为两点之间线段最短，所以当因为两点之间线段最短，所以当 I、F、N、H 在同一条直线上时在同一条直线上时NHFNFI最小最小 所以当所以当 I、F、N、H 在同一条直线上时，四边形在同一条直线上时，四边形 MDNF 的周长最小，的周长最小， 连接连接HI，交，交 x 轴于点轴于点 N，交，交 y 轴于点轴于点 F， 因为抛物线的表达式为因为抛物线的表达式为 2 23yxx ，所以点，所以点 M 的坐标为的坐标为(1,4)， 由轴对称的性质可得，由轴对称的性质可得，( 1, 4 )I ，( 2 ,3)H， 设直线设直线 HI 的表达式为的表达式为ymxn， 所

10、以所以 4 23 mn mn ， 解得解得 7 3 5 3 m n ， 所以直线所以直线 HI 的表达式为的表达式为 75 33 yx ， 当当0 x时，时， 5 3 y ， 当当0y 时，时， 75 0 33 x ，所以，所以 5 7 x ， 所以所以 5 (0, ) 3 F， 5 ( ,0) 7 N， 所以当所以当 M，D，N，F 为顶点的四边形周长最小时，为顶点的四边形周长最小时， 5 (0, ) 3 F， 5 ( ,0) 7 N （3）解：本题的答案为）解：本题的答案为92 15 第 25 题答图（1） 解题分析：如图（解题分析：如图（2） ，当两点） ，当两点 A、B 距离是定值，直

11、线距离是定值，直线 CD 是一条固定的直线，点是一条固定的直线，点 P 在直线在直线 CD 上移动，由下图可以看出只有当过上移动，由下图可以看出只有当过 A、B 的圆与直线的圆与直线 CD 相切时相切时APB最大最大 所以可作所以可作T过点过点 B、D，且与直线，且与直线 OC 相切，切点为相切，切点为 P，此时，此时BPD的度数最大，的度数最大， 由已知，可得由已知，可得OPt， (0, )Pt 因为直线因为直线 OC 与与T相切，相切， 所以所以TPOC， 所以直线所以直线 PT 的解析式为的解析式为yt 因为抛物线的表达式为因为抛物线的表达式为 2 23yxx ， 所以点所以点 B 的坐

12、标为的坐标为(3,0)， 因为点因为点 B(3,0)、点、点(2,3)D 可以求得直线可以求得直线 BD 的垂直平分线的解析式为的垂直平分线的解析式为 12 33 yx 联立联立yt与与 12 33 yx，得，得32xt，yt 直线直线 PT 与与直线直线 BD 的交点即为点的交点即为点 M，所以，所以(32, )Mtt 因为因为MBMC,可得可得 22 32(323)(0)ttt 解得解得92 15t 或或92 15t （舍去）（舍去） 所以当所以当92 15t 时时，BPD的度数最大的度数最大 27 （2019 江苏盐城卷，江苏盐城卷，27，14）如图所示，二次函数 2 (1)2yk x的

13、图象与一次函数2ykxk的图象交 于A,B两点，点B在点A的右侧，直线AB分别于x轴、y轴交于C、D两点，且0k . （1）求A,B两点横坐标； （2）若OAB 是以OA为腰的等腰三角形，求k的值； （3）二次函数图象的对称轴与x轴交于点E,是否存在实数k，使得2ODCBEC ，若存在，求出k的值；若 第 25 题答图（2） 第 25 题答图（3） 不存在，说明理由. 【解题过程】【解题过程】 （1）A、B 是与的交点 ， ， 点在点的右侧 ， 点横坐标是 ，点横坐标. （2）由（1）可知和 由两点间距离公式可得： OAB 是以为腰的等腰三角形 分为两种情况：或 当时即 当时即 或 综上所述，

14、或或. （3）存在，或 【提示】由（1）可知和.根据题意分为两种情况：点在点左侧，点在点右侧. 当点在点左侧时 y x D C B A O 2 (1)2yk x2ykxk 2 (1)2 2 yk x ykxk 2 (1)2= (1)2k xk x(1)(2)0k xx 1 1x 2 2x 1 1 =1 2 x y 2 2 =2 2+ x yk BA (1,2)A(2,2+k)B A1B2 (1,2)A(2,2+k)B (0,0)O 22 = 5,4(2) ,1OAOBkABk OA =OA AB=OA OB =OA AB 2 5=1k 2 4k 2k 0k 2k =OA OB 2 54(2)k

15、 2 (2)1k 1k 3k 1k 2k 3k 3k 47 3 k (1,2)A(2,2+k)B BCBC BC2+k00k-2 如图 1，过点作轴于点，作的垂直平分线交轴于点，连接 设=m ，由（1）可知和. 在 RtBFH 中，由得 ， 当点在点右侧时 如图，过点作轴于点，作的垂直平分线交轴于点，连接 由（1）可知和. 设 在 RtBMN 中，由得 BBHxHBExFBF =BF EF2BFHBEC =BF EF (1,2)A(2,2+k)B(1,0)E(2,0)H 1EH 1FHm 222 =BHFHBF 222 (2)(1)kmm 2 45 2 kk m 2 43 =1 2 kk FH

16、m 2 42 tan 43 BHk BFH FHkk 2ODCBEC =ODCBFHtantanODCBFH 2 (1,1)C k 2 =1OC k =2ODk 2 1 1 tan 2 OC k ODC ODkk 2 142 43 k kkk 3k 0k 3k 图图1 x y FH D C B A O E BC2+k0k-2 BBMxMBExNBN =BN EN2BNMBEC (1,2)A(2,2+k)B(1,0)E(2,0)M 1EM =nBN EN1MNn 222 BNMNBM 222 (2)(1)nkn 2 45 2 kk n 2 43 MN=1 2 kk n =(2)BMk 2 42

17、tan +4 +3 BMk BNM MNkk ， 综上所述，或. 23 （2019 江西省，江西省，23，12 分）分）特例感知特例感知 (1)如图如图 1， 对于抛物线， 对于抛物线1 2 1 xxy，12 2 2 xxy，13 2 3 xxy下列结论正确的序号是下列结论正确的序号是 ； 抛物线抛物线 1 y， 2 y， 3 y都经过点都经过点 C(0，1)； 抛物线抛物线 2 y， 3 y的对称轴由抛物线的对称轴由抛物线 1 y的对称轴依次向左平移的对称轴依次向左平移 2 1 个单位得到；个单位得到； 抛物线抛物线 1 y， 2 y， 3 y与直线与直线 y=1 的交点中，相邻两点之间的距

18、离相等的交点中，相邻两点之间的距离相等. 形成概念形成概念 (2)把满足把满足1 2 nxxyn（n 为正整数）的抛物线称为“系列平移抛物线”为正整数）的抛物线称为“系列平移抛物线”. 2ODCBEC =ODCBNMtantanODCBNM 2 (1,1)C k 2 =1OC k =2ODk 2 1 1 tan 2 OC k ODC ODkk 2 142 +4 +3 k kkk 2 3830kk 47 3 k 2k 47 3 k 图图2 y x N M D C B A OE 3k 47 3 k 知识应用知识应用 在在(2)中，如图中，如图 2. “系列平移抛物线”的顶点依次为“系列平移抛物线”

19、的顶点依次为 1 P， 2 P， 3 P， n P，用含，用含 n 的代数式表示顶点的代数式表示顶点 n P的坐标，并写出该顶的坐标，并写出该顶 点纵坐标点纵坐标 y 与横坐标与横坐标 x 之间的关系式；之间的关系式； “系列平移抛物线”存在“系列整数点“系列平移抛物线”存在“系列整数点(横、纵坐标均为整数的点横、纵坐标均为整数的点)” ：” ： 1 C， 2 C， 3 C， n C，其横坐标分别，其横坐标分别 为为-k-1，-k-2，-k-3，-k-n(k 为正整数为正整数)，判断相邻两点之间的距离是否都相等，若相等，直接写出相邻两点，判断相邻两点之间的距离是否都相等，若相等，直接写出相邻两

20、点 之间的距离；若不相等，说明理由；之间的距离；若不相等，说明理由； 在中， 直线在中， 直线 y=1 分别交 “系列平移抛物线” 于点分别交 “系列平移抛物线” 于点 1 A， 2 A， 3 A， ， ， n A， 连接， 连接 nnA C， 11nn AC， 判断， 判断 nnA C， 11nn AC是否平行？并说明理由是否平行？并说明理由. 【解题过程】解：【解题过程】解： （1）对于抛物线）对于抛物线1 2 1 xxy，12 2 2 xxy，13 2 3 xxy来说，来说， 抛物线抛物线 1 y， 2 y， 3 y都经过点都经过点 C(0，1)，正确；，正确； 抛物线抛物线 1 y，

21、2 y， 3 y的对称轴分别为：的对称轴分别为： 2 1 ) 1(2 1 1 x，1 ) 1(2 2 2 x， 2 3 ) 1(2 3 3 x的的 抛物线抛物线 2 y， 3 y的对称轴由抛物线的对称轴由抛物线 1 y的对称轴依次向左平移的对称轴依次向左平移 2 1 个单位得到，正确；个单位得到，正确； 抛物线抛物线 1 y， 2 y， 3 y与直线与直线 y=1 的另一个交点的横坐标分别为：的另一个交点的横坐标分别为：-1、-2、-3， 抛物线抛物线 1 y， 2 y， 3 y与直线与直线 y=1 的交点中，相邻两点之间的距离相等的交点中，相邻两点之间的距离相等.正确正确. 答案：答案： （

22、2）由由1 2 nxxyn可知，可知，顶点坐标为顶点坐标为 n P（ 2 n ， 4 4 2 n ） ，） ， 该顶点纵坐标该顶点纵坐标 y 与横坐标与横坐标 x 之间的关系式之间的关系式为为1 4 4)2( 4 4 2 22 x xn y； 当当横坐标分别为横坐标分别为-k-1，-k-2，-k-3，-k-n(k 为正整数为正整数)，对应的纵坐标为：对应的纵坐标为：1 2 kk，12 2 kk， 13 2 kk，1 2 nkk， 1 C 2 C 2222 )12() 1()2() 1(kkkkkk 2222 ) 121()21(kkkkkk 2 1 k， 2 C 3 C 2222 )13()

23、12()3()2(kkkkkk 2222 ) 1312()32(kkkkkk 2 1 k， ， 1n C n C 2222 )1( 1) 1()()1(nkkknknknk 2222 11) 1()1(nkkknknknk 2 1 k， 相邻两点的距离相等，且距离为：相邻两点的距离相等，且距离为： 2 1 k. 将将 y=1 代入代入1 2 nxxyn可得可得11 2 nxx，x=-n（0 舍去） ，舍去） ， 点点 1 A（-1，1） ，） ， 2 A（-2，1） ，） ， 3 A（-3，1） ，） ， n A（-n，1）. 当当横坐标分别为横坐标分别为-k-1，-k-2，-k-3，-k-n

24、(k 为正整数为正整数)，对应的纵坐标为：对应的纵坐标为：1 2 kk，12 2 kk， 13 2 kk，1 2 nkk， 点点 1 C（-k-1，1 2 kk） ，） ， 2 C（-k-2，12 2 kk） ，） ， 3 C（-k-3，13 2 kk） ， ，） ， ， n C（-k-n，1 2 nkk） . 设设 nnA C， 11nn AC的解析式分别为：的解析式分别为：y=px+q，y=mx+n， 则则 1)( 1 2 nkkqpnk qnp ， 1) 1()1( 1) 1( 2 knknmnk nmn ， 解得解得 p=k+n，m=k+n-1， pm nnA C， 11nn AC不平

25、行不平行. 23 （2019山西）山西）综合与探究 如图,抛物线 yax2+bx+6 经过点 A（2,0）,B(4,0)两点,与 y 轴交于点 C.点 D 是抛物线上一个动点,设点 D 的横 坐标为 m(1m4).连接 AC,BC,DB,DC. (1)求抛物线的函数表达式; (2)当BCD 的面积等于AOC 的面积的 3 4 时,求 m 的值; (3)在(2)的条件下,若点M是x轴上一动点,点N是抛物线上一动点,试判断是否存在这样的点M,使得以点B,D,M,N 为顶点的四边形是平行四边形.若存在,请直接写出点 M 的坐标;若不存在,请说明理由. 第 23 题图 【解题过程】【解题过程】(1)抛

26、物线 yax2+bx+6 经过点 A（2,0）,B(4,0)两点, 4260 16460 ab ab ,解之,得: 3 4 3 2 a b ,抛 物线的函数表达式为: 2 33 6 42 yxx ; (2)作直线 DEx 轴于点 E,交 BC 于点 G,作 CFDE,垂足为点 F,点 A 的坐标为(2,0),OA2,由 x0,得 y 6,点 C 的坐标为(0,6),OC6,SAOC 1 2 OAOC6,SBCD 3 4 SAOC 9 2 .设直线 BC 的函数表达式为 y kx+n,由B,C两点的坐标得: 40 6 kn n ,解之,得: 3 2 6 k n ,直线BC的函数表达式为:y 3

27、2 x+6.点G的坐标 为(m, 3 2 m+6),DG 2 33 6 42 mm( 3 2 m+6) 2 3 3 4 mm.点 B 的坐标为(4,0),OB4,SBCDS CDG+SBDG 2 3 6 4 mm. 2 3 6 4 mm 9 2 ,解之,得 m13,m21,m 的值为 3. 第 23 题答图 (3)存在点 M,其坐标为:M1(8,0),M2(0,0),M3(14,0),M4(14,0). 25 （2019常德常德）如图11，已知二次函数图象的顶点坐标为A（1，4），与坐标轴交于B、C、D三点，且B点的 坐标为（1，0） （1）求二次函数的解析式； （2） 在二次函数图象位于x轴

28、上方部分有两个动点M、 N， 且点N在点M的左侧， 过M、 N作x轴的垂线交x轴于点G、 H两点，当四边形MNHG为矩形时，求该矩形周长的最大值； （3） 当矩形MNHG的周长最大时， 能否在二次函数图象上找到一点P， 使PNC的面积是矩形MNHG面积的 9 16 ， 若存在，求出该点的横坐标，若不存在，请说明理由 【解题过程】【解题过程】 （1）设抛物线的解析式为 y 2 14a x ，把 B（1，0）代入解析式得：4a40，解得 a 1，y 2 14x 2 23xx； （2）四边形 MNHG 为矩形，MNx 轴，设 MGNHn，把 y n 代入 y 2 23xx， 即 n 2 23xx，

29、2 23xxn0， 由根与系数关系得 MN xx2，M N xx n3， 2 MN xx 2 + MN xx4 MN xx， 2 MN xx44（n3）164n，MN 2 MN xx 24n，设矩形 MNHG 周长为 C，则 C2（MNMG）2（24nn）44n2n，令4n t， 则 n4 2 t， C2 2 t4t82 2 110t ， 20， t1 时， 周长有最大值， 最大值为 10； （3）在（2）的条件下，当矩形周长最大时 t1，4n1，n3，MN24n2，D（0，3） ，此 时 N 与 D 重合， MNHG S236， PNC S 9 16 MNHG S 27 8 ， 又当 y0

30、时 0 2 23xx， 解得 1 x 1， 2 x3，C（3，0） ，D（0，3） ，直线 CD 的解析式为 yx+3，过 P 做 y 轴的平行线，交 直线 CD 于点 Q， 设 P 横坐标为 m， 则 P （m， 2 23mm） ， Q （m， 3m ） ， PQ （ 2 23mm） （3m ），当 P 在 Q 的上方时，PQ 2 3mm， PNC S 1 2 PQOC 27 8 ， 2 3mm 9 4 ， 解得 m 3 2 ； 当 P 在 Q 的下方时， PQ 2 3mm， 即 2 3mm 9 4 ， 解得 1 33 2 2 m ， 2 3+3 2 2 m （舍去） ； P 横坐标为 3

31、2 或 33 2 2 x x y y 备用图图11 C A D B BH N G D A M C O O 25 （2019衡阳衡阳）如图，二次函数 yx2bxc 的图象与 x 轴交于点 A（1，0）和点 B（3，0），与 y 轴交 于点 N，以 AB 为边在 x 轴上方作正方形 ABCD，点 P 是 x 轴上一动点，连接 CP，过点 P 作 CP 的垂线与 y 轴交 于点 E. （1）求该抛物线的函数关系表达式； （2）当点 P 在线段 OB（点 P 不与 O、B 重合）上运动至何处时，线段 OE 的长有最大值？并求出这个最大值； （3）在第四象限的抛物线上任取一点 M，连接 MN、MB，请问

32、：MBN 的面积是否存在最大值？若存在，求 出此时点 M 的坐标；若不存在，请说明理由. 解：（1）把 A（1，0），B（3，0）代入 yx2bxc，得 01, 093, bc bc 解得 2, 3. b c 该抛物线的函数表达式为 yx22 x3； （2）CPEB，OPEBCP90 ，OPEOEP90 ，OEPBPC，tanOEPtan BPC OP OE BC PB 设 OEy，OPx， y x 4 3x 整理，得 y 1 4 x2x 1 4 （x 3 2 ）2 9 16 当 OP 3 2 时，OE 有最大值，最大值为 9 16 ，此时点 P 在（ 3 2 ，0）处. （3）过点 M 作

33、MFx 轴交 BN 于点 F， N（0，3），B（3，0），直线的解析式为 y3 m. 设 M（m, m22 m3）,则 MFm23m， x y P (N) (H) 备用图 C M A D G Q B P O x y E CD N BAOP M MBN 的面积 1 2 OB MF 3 2 ( m23m) 3 2 ( m 3 2 ) 2 27 8 . 点 M 的坐标为（ 3 2 ， 27 8 ）时，MBN 的面积存在最大值. 24 （2019武汉，24，12 分）分）已知抛物线 C1：y（x1）24 和 C2：yx2 （1） 如何将抛物线 C1平移得到抛物线 C2？ （2） 如图 1，抛物线 C

34、1与 x 轴正半轴交于点 A，直线 4 3 yxb 经过点 A，交抛物线 C1于另一点 B请你在线段 AB 上取点 P，过点 P 作直线 PQy 轴交抛物线 C1于点 Q，连接 AQ 若 APAQ，求点 P 的横坐标 若 PAPQ，直接写出点 P 的横坐标 （3） 如图 2，MNE 的顶点 M、N 在抛物线 C2上，点 M 在点 N 右边，两条直线 ME、NE 与抛物线 C2均有唯一公 共点，ME、NE 均与 y 轴不平行若MNE 的面积为 2，设 M、N 两点的横坐标分别为 m、n，求 m 与 n 的数量关系 【解题过程】【解题过程】 （1）先向左平移1个单位，在向上平移4个单位 （2）kA

35、B 4 3 和A（3，0）易求AB：y 4 4 3 x APAQ，PQAOPAOQAO AQ：y 4 4 3 x 联立 2 4 4 3 33 yx yxx 得 2 3-10 +3=0 xx 1 3 Q x 设P（t， 4 -+4 3 x）则Q（t， 2-2 +3 tt）易求：PQ 2 2 +7 3 tt，PA 5 3 3 t PAPQ x y F E CD N BA OP M 2 3760tt 2 3 Q x （3）设 ME： 2 1 ykxmm 联立 2 1 2 ykxmm yx 则 22 11 0 xk xk mm 22 11 44kk mm 2 11 202kmkm即 2 2MEymxm

36、： 同理： 2 2NEynxn： 2222 , 2 111 ()2 22222 mn Emn mnmn nmnmmnmnnmnnmmnm 化简得： 3 3 () ()4 2 mn mn 3 ()82mnmn即 25 （2019黄冈黄冈）如图在平面直角坐标系 xOy 中，已知 A(2，2)，B(2，0)，C(0，2)，D(2，0)四点，动 点 M 以每秒2个单位长度的速度沿 BCD 运动(M 不与点 B、点 D 重合)，设运动时间为 t(秒). (1)求经过 A、C、D 三点的抛物线的解析式； (2)点 P 在(1)中的抛物线上，当 M 为 BC 的中点时，若 PAMPBM，求点 P 的坐标；

37、(3)当 M 在 CD 上运动时，如图.过点 M 作 MFx 轴，垂足为 F，MEAB，垂足为 E.设矩形 MEBF 与 BCD 重叠部分的面积为 S，求 S 与 t 的函数关系式，并求出 S 的最大值； (4)点 Q 为 x 轴上一点，直线 AQ 与直线 BC 交于点 H，与 y 轴交于点 K.是否存在点 Q，使得 HOK 为等腰三角 形?若存在，直接写出符合条件的所有 Q 点的坐标；若不存在，请说明理由. 【解题过程】【解题过程】 28 （2019陇南陇南）如图，抛物线 yax2+bx+4 交 x 轴于 A（3，0） ，B（4，0）两点，与 y 轴交于点 C，连接 AC，BC点 P 是第一

38、象限内抛物线上的一个动点，点 P 的横坐标为 m （1）求此抛物线的表达式； （2） 过点 P 作 PMx 轴， 垂足为点 M， PM 交 BC 于点 Q 试探究点 P 在运动过程中， 是否存在这样的点 Q， 使得以 A，C，Q 为顶点的三角形是等腰三角形若存在，请求出此时点 Q 的坐标，若不存在，请说明理由； （3）过点 P 作 PNBC，垂足为点 N请用含 m 的代数式表示线段 PN 的长，并求出当 m 为何值时 PN 有最 大值，最大值是多少？ 解： （1）由二次函数交点式表达式得：ya（x+3） （x4）a（x2x12）= ax2ax12a， 抛物线 yax2+bx+4， 12a4，解

39、得：a， 抛物线的表达式为 yx2+x+4； （2）存在，理由： 点 A、B、C 的坐标分别为（3，0） 、 （4，0） 、 （0，4） ， 则 AC5，AB7，BC4，OABOBA45， 将点 B、C 的坐标代入一次函数表达式：ykx+b 并解得：yx+4， 同理可得直线 AC 的表达式为：yx+4， 设直线 AC 的中点为 P（，4） ，过点 P 与 CA 垂直直线的表达式中的 k 值为， 同理可得过点 P 与直线 AC 垂直直线的表达式为：yx+， 当 ACAQ 时，如图 1， 则 ACAQ5， 设：QMMBn，则 AM7n， 由勾股定理得： （7n）2+n225，解得：n3 或 4（舍

40、去 4） ， 故点 Q（1，3） ； 当 ACCQ 时，如图 1， CQ5，则 BQBCCQ45， 则 QMMB， 故点 Q（，） ； 当 CQAQ 时， 联立并解得：x（舍去） ； 故点 Q 的坐标为：Q（1，3）或（，） ； （3）设点 P（m，m2+m+4） ，则点 Q（m，m+4） ， OBOC，ABCOCB45PQN， PNPQsinPQN（m2+m+4+m4）m2+m， 0，PN 有最大值， 当 m时，PN 的最大值为： 1. （2019湖州）如图 1，在平面直角坐标系 xOy 中，四边形 OABC 是矩形，点 A，C 分别在 x 轴和 y 轴的正半 轴上，连结 AC，OA3，ta

41、nOAC 3 3 ，D 是 BC 的中点 （1）求 OC 的长及点 D 的坐标； （2）如图 2，M 是线段 OC 上的点，OM 2 3 OC，点 P 是线段 OM 上的一个动点，经过 P，D，B 三点的 抛物线交 x 轴的正半轴于点 E，连结 DE 交 AB 于点 F 将DBF 沿 DE 所在的直线翻折，若点 B 恰好落在 AC 上，求此时 BF 的长和点 E 的坐标； 以线段 DF 为边，在 DF 所在的直线的右上方作等边DFG，当动点 P 从点 O 运动到点 M 时，点 G 也随之运动，请直接写出 点 G 的运动路径的长 【思路分析】【思路分析】 （1）RtAOC 中，由正切三角函数，可

42、求 OC 的长；再由矩形的性质及线段中点的定义锁定点 D y x DC B AO F E P M y x D C B A O 的坐标（2） 由翻折可知 DB DB DC， 从而DCADBC30 通过解直角三角形得到 FAFB 3 2 ， 在 RtAEF 中， AEAFtanAFE 3 2 3 3 2 ， 从而求得点 E 的坐标 按一找点 G 的运动起点与终点， 从而找到点 G 的路径，二求该路径的长即可锁定答案如答图 2 和答图 3，表示动点 P 从点 O 运动到点 M 时， 点 G 也随之运动时的起点、与终点的位置，G 点的路径是一条线段 【解题过程】【解题过程】 （1） 在 RtAOC 中

43、， 由 tanOAC 3 3 OC OA ， OA3， 得 OCOAtanOAC3 3 3 3 四边形 OABC 是矩形，点 D 为 BC 的中点， D( 3 2 ，3) （2）如答图 1，易知OACACB30 而由折叠可知 DB DB DC，从而DCADBC30 BDFBDF30 DFBAFE60 RtDBF 中，易求 BF 3 2 AFABBF 3 2 RtAEF 中，AEAFtanAFE 3 2 3 3 2 OE 9 2 ，E( 9 2 ，0) 综上，BF 的长为 3 2 ，点 E 的坐标为 E( 9 2 ，0) 3 6 【知识点】【知识点】矩形性质；解直角三角形；翻折（轴对称） ；等腰

44、三角形；等边三角形；二次函数；动态问题；数形 结合思想；探究性问题；压轴题；原创题 2. （2019天津）在平面直角坐标系中，O 为原点，点 A(6，0),点 B 在 y 轴的正半轴上，ABO=30 ，矩形 CODE 的顶点 D,E,C 分别在 OA,AB,OB 上，OD=2. （1）如图，求点 E 的坐标； （2）将矩形 CODE 沿 x 轴向右平移，得到矩形 CODE,点 C,O,D,E 的对应点分别为 C,O,D,E,设 OO=t, 矩形 CODE与ABO 重叠部分的面积为 S 如图，当矩形 CODE与ABO 重叠部分为五边形时，CE,ED分别与 AB 相交于点 M,F，试用含有 t 的

45、式子表示 S，并直接写出 t 的取值范围； 当35 3S 时，求 t 的取值范围（直接写出结果即可） 【思路分析】(1)由题意知 OA=6，OD=2，AD=4，由矩形 CODE 得 DEBO，AED=ABO=30 ， DE=tan60 AD=4 3，所以点 E 的坐标为（2，4 3） （2）由平移得，OC=DE=4 3,OD=CE=2，ME=OO=t，根据 EDBO，得EFM=OBA=30 ,Rt 第 24 题答图 3 M P G F E DC B A O y x 第 24 题答图 2 G F E P M D C B A O y x 第 24 题答图 1 MEF 中，EF=3t， SMEF=

46、2 113 3 222 ME FEttt；S矩形CODE=4 3 28 3C O O D ; S=S矩形CODE-SMEF= 2 3 t +8 3 2 ，因为重叠部分是五边形，所以 t 的取值范围是 0t2； 当 S=3时， 2 3 t +8 3 2 =3， 此时 t=142， 所以重叠部分不是五边形； 当 S=5 3时， 2 3 t +8 3 2 =5 3，此时 t=62，所以重叠部分不是五边形；当 2t4 时，重叠部分是四边形如图所示，当 4t6 时， 重叠部分是三角形如图所示. 当 2t4 时, 11 ()( 3(6)3(4) 23(102t) 22 SMOFDO Dtt 当 4t6 时, 2 113 (6t)3(6)(6) 222 SO A O Mtt 所以，当 S=3时，3(102t)= 3S ，此时 t=4.5,不在 2t4 范围内； 当 S=5 3时3(102t)=5 3S ，此时 t=2.5； 当 S=3时， 2 3 =(6) = 3 2 St，此时 t=6- 2， 综上所述，t