2020-2021学年人教版八年级数学下册《第十七章 勾股定理》复习题（含答案解析）

《2020-2021学年人教版八年级数学下册《第十七章 勾股定理》复习题（含答案解析）》由会员分享，可在线阅读，更多相关《2020-2021学年人教版八年级数学下册《第十七章 勾股定理》复习题（含答案解析）（38页珍藏版）》请在七七文库上搜索。

1、第十七章第十七章 勾股定理勾股定理 复习题复习题 一选择题（共一选择题（共 18 小题）小题） 1如图，将两个完全相同的 RtACB 和 RtACB拼在一起，其中点 A与点 B 重合，点 C在边 AB 上， 连接 BC，若ABCABC30，ACAC2，则 BC 的长为（ ） A2 B4 C2 D4 2如图，RtABC 中，ACB90，AB5，AC3，把 RtABC 沿直线 BC 向右平移 3 个单位长度得 到ABC，则四边形 ABCA的面积是（ ） A15 B18 C20 D22 3 九章算术是我国古代数学的经典著作，书中有一个“折竹抵地”问题： “今有竹高丈，末折抵地，问 折者高几何？“意思

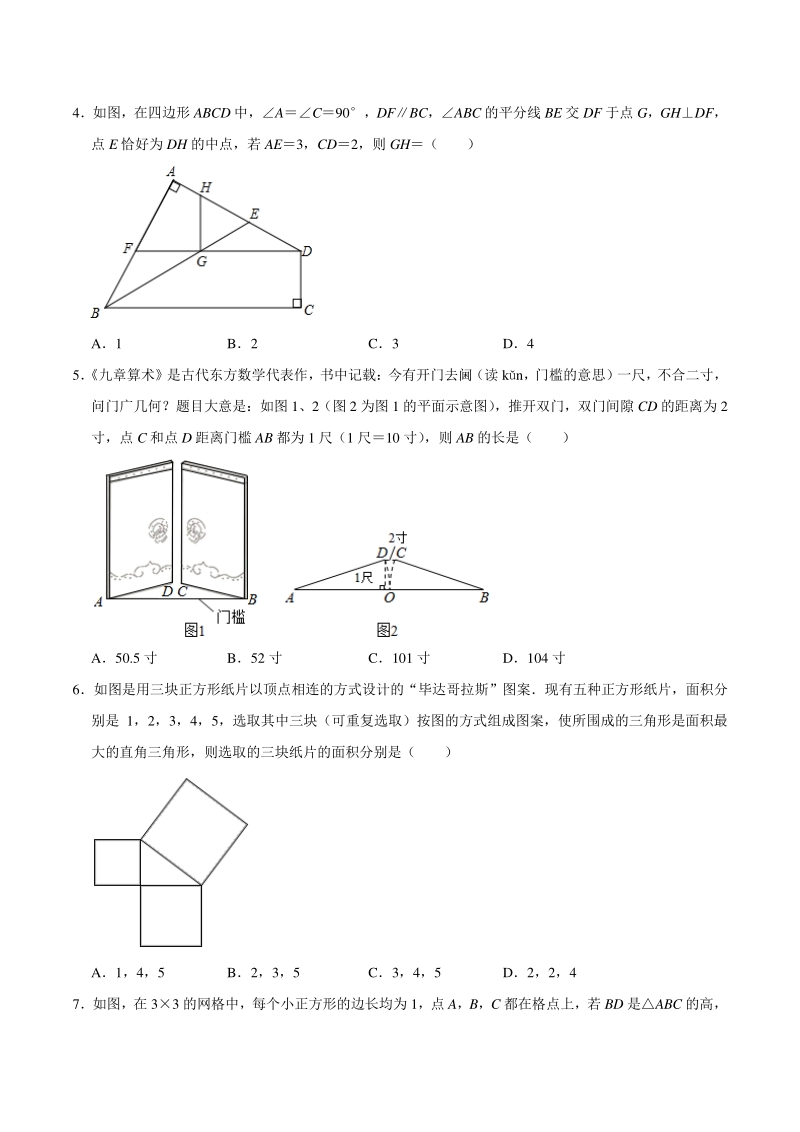
2、是：一根竹子，原来高一丈（一丈为十尺） ，虫伤有病，一阵风将竹子折断，其竹梢 恰好抵地，抵地处离原竹子根部三尺远，问：原处还有多高的竹子？（ ） A4 尺 B4.55 尺 C5 尺 D5.55 尺 4如图，在四边形 ABCD 中，AC90，DFBC，ABC 的平分线 BE 交 DF 于点 G，GHDF， 点 E 恰好为 DH 的中点，若 AE3，CD2，则 GH（ ） A1 B2 C3 D4 5 九章算术是古代东方数学代表作，书中记载：今有开门去阃（读 kn，门槛的意思）一尺，不合二寸， 问门广几何？题目大意是：如图 1、2（图 2 为图 1 的平面示意图） ，推开双门，双门间隙 CD 的距离

3、为 2 寸，点 C 和点 D 距离门槛 AB 都为 1 尺（1 尺10 寸） ，则 AB 的长是（ ） A50.5 寸 B52 寸 C101 寸 D104 寸 6如图是用三块正方形纸片以顶点相连的方式设计的“毕达哥拉斯”图案现有五种正方形纸片，面积分 别是 1，2，3，4，5，选取其中三块（可重复选取）按图的方式组成图案，使所围成的三角形是面积最 大的直角三角形，则选取的三块纸片的面积分别是（ ） A1，4，5 B2，3，5 C3，4，5 D2，2，4 7如图，在 33 的网格中，每个小正方形的边长均为 1，点 A，B，C 都在格点上，若 BD 是ABC 的高， 则 BD 的长为（ ） A B

4、 C D 8如图，从笔直的公路 l 旁一点 P 出发，向西走 6km 到达 l；从 P 出发向北走 6km 也到达 l下列说法错误 的是（ ） A从点 P 向北偏西 45走 3km 到达 l B公路 l 的走向是南偏西 45 C公路 l 的走向是北偏东 45 D从点 P 向北走 3km 后，再向西走 3km 到达 l 9如图，四个全等的直角三角形拼成“赵爽弦图” ，得到正方形 ABCD 与正方形 EFGH连接 EG，BD 相 交于点 O、BD 与 HC 相交于点 P若 GOGP，则的值是（ ） A1+ B2+ C5 D 10如图，在正方形网格（每个小正方形的边长都是 1）中，若将ABC 沿 A

5、D 的方向平移 AD 长，得 DEF（B、C 的对应点分别为 E、F） ，则 BE 长为（ ） A1 B2 C D3 11如图，点 E 在正方形 ABCD 的边 AB 上，若 EB1，EC2，那么正方形 ABCD 的面积为（ ） A B3 C D5 12如图，在四边形 ABCD 中，ADBC，D90，AD4，BC3分别以点 A，C 为圆心，大于AC 长为半径作弧，两弧交于点 E，作射线 BE 交 AD 于点 F，交 AC 于点 O若点 O 是 AC 的中点，则 CD 的长为（ ） A2 B4 C3 D 13下列四组数据中，不能作为直角三角形的三边长的是（ ） A6，8，10 B10，15，20

6、 C5，12，13 D7，24，25 14勾股定理是人类最伟大的科学发现之一，在我国古算书周髀算经中早有记载如图，以直角三角 形的各边为边分别向外作正三角形， 再把较小的两张正三角形纸片按图的方式放置在最大正三角形内 若 知道图中阴影部分的面积，则一定能求出（ ） A直角三角形的面积 B最大正三角形的面积 C较小两个正三角形重叠部分的面积 D最大正三角形与直角三角形的面积和 15在算法统宗中有一道“荡秋千”的问题： “平地秋千未起，踏板一尺离地送行二步与人齐，五尺 人高曾记仕女佳人争蹴，终朝笑语欢嬉良工高士素好奇，算出索长有几 ”此问题可理解为：如图， 有一架秋千， 当它静止时， 踏板离地距离

7、 AB 长度为 1 尺 将它往前水平推送 10 尺时， 即 AC10 尺， 则此时秋千的踏板离地距离 AD 就和身高 5 尺的人一样高若运动过程中秋千的绳索始终拉得很直， 则绳索 OA 长为（ ） A13.5 尺 B14 尺 C14.5 尺 D15 尺 16如图，某公园内的一块草坪是长方形 ABCD，已知 AB8m，BC6m，公园管理处为了方便群众，沿 AC 修了一条近道，一个人从 A 到 C 走 ABC 比直接走 AC 多走了（ ） A2 米 B4 米 C6 米 D8 米 17下列条件中，不能判断ABC（a、b、c 为三边，A、B、C 为三内角）为直角三角形的是（ ） Aa21，b22，c2

8、3 Ba：b：c3：4：5 CA+BC DA：B：C3：4：5 二填空题（共二填空题（共 10 小题）小题） 18如图，四边形 ABCD 中，ABCD，ABC60，ADBCCD4，点 M 是四边形 ABCD 内的一个 动点，满足AMD90，则点 M 到直线 BC 的距离的最小值为 19对角线互相垂直的四边形叫做“垂美”四边形，现有如图所示的“垂美”四边形 ABCD，对角线 AC、 BD 交于点 O若 AD2，BC4，则 AB2+CD2 20如图 1，四个全等的直角三角形围成一个大正方形，中间是个小正方形，这个图形是我国汉代赵爽在注 解周髀算经时给出的，人们称它为“赵爽弦图” 在此图形中连接四条

9、线段得到如图 2 的图案，记阴 影部分的面积为 S1，空白部分的面积为 S2，大正方形的边长为 m，小正方形的边长为 n，若 S1S2，则 的值为 21 九章算术是中国传统数学的重要著作之一，奠定了中国传统数学的基本框架如图所示是其中记载 的一道“折竹”问题： “今有竹高一丈，末折抵地，去根三尺，问折者高几何？”题意是：一根竹子原高 1 丈（1 丈10 尺） ，中部有一处折断，竹梢触地面处离竹根 3 尺，试问折断处离地面多高？答：折断处 离地面 尺高 22 如图， 在ABC 中， 已知 AB2， ADBC， 垂足为 D， BD2CD 若 E 是 AD 的中点， 则 EC 23如图，ABC 中，

10、点 E 在边 AC 上，EBEA，A2CBE，CD 垂直于 BE 的延长线于点 D，BD8， AC11，则边 BC 的长为 24在 RtABC 中，C90，若 ABAC2，BC8，则 AB 的长是 25如图，已知边长为 2 的等边三角形 ABC 中，分别以点 A，C 为圆心，m 为半径作弧，两弧交于点 D， 连接 BD若 BD 的长为 2，则 m 的值为 26勘测队按实际需要构建了平面直角坐标系，并标示了 A，B，C 三地的坐标，数据如图（单位：km） 笔 直铁路经过 A，B 两地 （1）A，B 间的距离为 km； （2）计划修一条从 C 到铁路 AB 的最短公路 l，并在 l 上建一个维修站

11、 D，使 D 到 A，C 的距离相等， 则 C，D 间的距离为 km 27如图，AB 与 CD 相交于点 O，ABCD，AOC60，ACD+ABD210，则线段 AB，AC，BD 之间的等量关系式为 三解答题（共三解答题（共 5 小题）小题） 28阅读与思考 如图是小宇同学的数学日记，请仔细阅读，并完成相应的任务 年月日星期日 没有直角尺也能作出直角 今天，我在书店一本书上看到下面材料：木工师傅有一块如图所示的四边形木板，他已经在木板上画出 一条裁割线 AB，现根据木板的情况，要过 AB 上的一点 C，作出 AB 的垂线，用锯子进行裁割，然而手头 没有直角尺，怎么办呢？ 办法一：如图，可利用一

12、把有刻度的直尺在 AB 上量出 CD30cm，然后分别以 D，C 为圆心，以 50cm 与 40cm 为半径画圆弧，两弧相交于点 E，作直线 CE，则DCE 必为 90 办法二：如图，可以取一根笔直的木棒，用铅笔在木棒上点出 M，N 两点，然后把木棒斜放在木板上， 使点 M 与点 C 重合，用铅笔在木板上将点 N 对应的位置标记为点 Q，保持点 N 不动，将木棒绕点 N 旋转， 使点 M 落在 AB 上，在木板上将点 M 对应的位置标记为点 R然后将 RQ 延长，在延长线上截取线段 QS MN，得到点 S，作直线 SC，则RCS90 我有如下思考：以上两种办法依据的是什么数学原理呢？我还有什么

13、办法不用直角尺也能作出垂线 呢？ 任务： （1）填空： “办法一”依据的一个数学定理是 ； （2）根据“办法二”的操作过程，证明RCS90； （3）尺规作图：请在图的木板上，过点 C 作出 AB 的垂线（在木板上保留作图痕迹，不写作法） ； 说明你的作法所依据的数学定理或基本事实（写出一个即可） 29在ABC 中，ABc，BCa，ACb如图 1，若C90时，根据勾股定理有 a2+b2c2 （1）如图 2，当ABC 为锐角三角形时，类比勾股定理，判断 a2+b2与 c2的大小关系，并证明； （2）如图 3，当ABC 为钝角三角形时，类比勾股定理，判断 a2+b2与 c2的大小关系，并证明； （3

14、）如图 4，一块四边形的试验田 ABCD，已知B90，AB80 米，BC60 米，CD90 米，AD 110 米，求这块试验田的面积 30如图，在离水面高度为 5 米的岸上，有人用绳子拉船靠岸，开始时拉紧的绳子 BC 的长为 13 米，此人 把绳子收紧 4 米后船移动到点 D 的位置（即绳子 CD 的长为 9 米） ，问船向岸边移动了多少米？（结果 保留根号） 31如图所示，某住宅小区在相邻两楼之间修建一个上方是半圆，下方是长方形的仿古通道，已知长方形 的长 AB4 米，宽 BC2.6 米现有一辆卡车装满家具后，高 4 米，宽 2 米，请问这辆送家具的卡车能 否通过这个通道？（参考数据：1.7

15、） 32如图，把一块直角三角形（ABC，ACB90）土地划出一个三角形（ADC）后，测得 CD3 米，AD4 米，BC12 米，AB13 米 （1）求证：ADC90； （2）求图中阴影部分土地的面积 第十七章第十七章 勾股定理勾股定理 复习题复习题 参考答案与试题解析参考答案与试题解析 一选择题（共一选择题（共 18 小题）小题） 1如图，将两个完全相同的 RtACB 和 RtACB拼在一起，其中点 A与点 B 重合，点 C在边 AB 上， 连接 BC，若ABCABC30，ACAC2，则 BC 的长为（ ） A2 B4 C2 D4 【分析】 根据直角三角形的性质求出 AB4， AB4， 根据勾

16、股定理求出 BC， 再根据勾股定理计算， 得到答案 【解答】解：ACBACB90，ABCABC30，ACAC4， AB4，AB4， BC2， RtACBRtACB， BACA， CBB90， BC2， 故选：A 【点评】本题考查的是勾股定理、全等三角形的性质、含 30的直角三角形的性质，如果直角三角形的 两条直角边长分别是 a，b，斜边长为 c，那么 a2+b2c2 2如图，RtABC 中，ACB90，AB5，AC3，把 RtABC 沿直线 BC 向右平移 3 个单位长度得 到ABC，则四边形 ABCA的面积是（ ） A15 B18 C20 D22 【分析】 根据平移的性质得到 AACC3，

17、AABC， 由勾股定理得到 BC4， 根据梯形的面积公式即可得到结论 【解答】解：把 RtABC 沿直线 BC 向右平移 3 个单位长度得到ABC， AACC3，AABC， 在 RtABC 中， AB5，AC3， BC4， AABC， 四边形 ABCA是梯形， 四边形 ABCA的面积（AA+BC） AC（3+4+3）315， 故选：A 【点评】本题考查了勾股定理，梯形的面积，平移的性质等知识点的应用，主要考查学生综合运用性质 进行计算的能力，题目比较典型，但难度不大 3 九章算术是我国古代数学的经典著作，书中有一个“折竹抵地”问题： “今有竹高丈，末折抵地，问 折者高几何？“意思是：一根竹子，

18、原来高一丈（一丈为十尺） ，虫伤有病，一阵风将竹子折断，其竹梢 恰好抵地，抵地处离原竹子根部三尺远，问：原处还有多高的竹子？（ ） A4 尺 B4.55 尺 C5 尺 D5.55 尺 【分析】竹子折断后刚好构成一直角三角形，设竹子折断处离地面 x 尺，则斜边为（10 x）尺利用勾 股定理解题即可 【解答】解：设竹子折断处离地面 x 尺，则斜边为（10 x）尺， 根据勾股定理得：x2+32（10 x）2 解得：x4.55 答：原处还有 4.55 尺高的竹子 故选：B 【点评】此题考查了勾股定理的应用，解题的关键是利用题目信息构造直角三角形，从而运用勾股定理 解题 4如图，在四边形 ABCD 中，

19、AC90，DFBC，ABC 的平分线 BE 交 DF 于点 G，GHDF， 点 E 恰好为 DH 的中点，若 AE3，CD2，则 GH（ ） A1 B2 C3 D4 【分析】过 E 作 EMBC，交 FD 于点 N，可得 ENGD，得到 EN 与 GH 平行，再由 E 为 HD 中点，得 到 HG2EN，同时得到四边形 NMCD 为矩形，再由角平分线定理得到 AEME，进而求出 EN 的长，得 到 HG 的长 【解答】解：过 E 作 EMBC，交 FD 于点 N， DFBC， ENDF， ENHG， DENDHG，ENDHGD， ENDHGD， ， E 为 HD 中点， ， ，即 HG2EN，

20、 DNMNMCC90， 四边形 NMCD 为矩形， MNDC2， BE 平分ABC，EAAB，EMBC， EMAE3， ENEMMN321， 则 HG2EN2 故选：B 【点评】此题考查了勾股定理，矩形的判定与性质，角平分线定理，以及平行线分线段成比例，熟练掌 握定理及性质是解本题的关键 5 九章算术是古代东方数学代表作，书中记载：今有开门去阃（读 kn，门槛的意思）一尺，不合二寸， 问门广几何？题目大意是：如图 1、2（图 2 为图 1 的平面示意图） ，推开双门，双门间隙 CD 的距离为 2 寸，点 C 和点 D 距离门槛 AB 都为 1 尺（1 尺10 寸） ，则 AB 的长是（ ） A

21、50.5 寸 B52 寸 C101 寸 D104 寸 【分析】取 AB 的中点 O，过 D 作 DEAB 于 E，根据勾股定理解答即可得到结论 【解答】解：取 AB 的中点 O，过 D 作 DEAB 于 E，如图 2 所示： 由题意得：OAOBADBC， 设 OAOBADBCr 寸， 则 AB2r，DE10，OECD1，AEr1， 在 RtADE 中， AE2+DE2AD2，即（r1）2+102r2， 解得：r50.5， 2r101（寸） ， AB101 寸， 故选：C 【点评】本题考查了勾股定理的应用，弄懂题意，构建直角三角形是解题的关键 6如图是用三块正方形纸片以顶点相连的方式设计的“毕达

22、哥拉斯”图案现有五种正方形纸片，面积分 别是 1，2，3，4，5，选取其中三块（可重复选取）按图的方式组成图案，使所围成的三角形是面积最 大的直角三角形，则选取的三块纸片的面积分别是（ ） A1，4，5 B2，3，5 C3，4，5 D2，2，4 【分析】根据题意可知，三块正方形的面积中，两个较小的面积之和等于最大的面积，再根据三角形的 面积，分别计算出各个选项中围成的直角三角形的面积，比较大小，即可解答本题 【解答】解：当选取的三块纸片的面积分别是 1，4，5 时，围成的直角三角形的面积是， 当选取的三块纸片的面积分别是 2，3，5 时，围成的直角三角形的面积是； 当选取的三块纸片的面积分别是

23、 3，4，5 时，围成的三角形不是直角三角形； 当选取的三块纸片的面积分别是 2，2，4 时，围成的直角三角形的面积是， ， 所围成的三角形是面积最大的直角三角形，则选取的三块纸片的面积分别是 2，3，5， 故选：B 【点评】本题考查勾股定理的逆定理，解答本题的关键是明确题意，利用勾股定理的逆定理解答 7如图，在 33 的网格中，每个小正方形的边长均为 1，点 A，B，C 都在格点上，若 BD 是ABC 的高， 则 BD 的长为（ ） A B C D 【分析】根据勾股定理计算 AC 的长，利用面积差可得三角形 ABC 的面积，由三角形的面积公式即可得 到结论 【解答】解：由勾股定理得：AC，

24、SABC333.5， ， ， BD， 故选：D 【点评】本题考查了勾股定理，三角形的面积的计算，掌握勾股定理是解题的关键 8如图，从笔直的公路 l 旁一点 P 出发，向西走 6km 到达 l；从 P 出发向北走 6km 也到达 l下列说法错误 的是（ ） A从点 P 向北偏西 45走 3km 到达 l B公路 l 的走向是南偏西 45 C公路 l 的走向是北偏东 45 D从点 P 向北走 3km 后，再向西走 3km 到达 l 【分析】先作出图形，根据勾股定理和等腰直角三角形的性质即可求解 【解答】解：如图， 由题意可得PAB 是腰长 6km 的等腰直角三角形， 则 AB6km， 如图所示，过

25、 P 点作 AB 的垂线 PC， 则 PC3km， 则从点 P 向北偏西 45走 3km 到达 l，选项 A 错误； 则公路 l 的走向是南偏西 45或北偏东 45，选项 B，C 正确； 则从点 P 向北走 3km 后到达 BP 中点 D， 此时 CD 为PAB 的中位线， 故 CDAP3， 故再向西走 3km 到达 l，选项 D 正确 故选：A 【点评】本题考查的是勾股定理的应用，关键是从题中抽象出勾股定理这一数学模型，画出准确的示意 图领会数形结合的思想的应用 9如图，四个全等的直角三角形拼成“赵爽弦图” ，得到正方形 ABCD 与正方形 EFGH连接 EG，BD 相 交于点 O、BD 与

26、 HC 相交于点 P若 GOGP，则的值是（ ） A1+ B2+ C5 D 【分析】证明BPGBCG（ASA） ，得出 PGCG设 OGPGCGx，则 EG2x，FGx， 由勾股定理得出 BC2（4+2）x2，则可得出答案 【解答】解：四边形 EFGH 为正方形， EGH45，FGH90， OGGP， GOPOPG67.5， PBG22.5， 又DBC45， GBC22.5， PBGGBC， BGPBGC90，BGBG， BPGBCG（ASA） ， PGCG 设 OGPGCGx， O 为 EG，BD 的交点， EG2x，FGx， 四个全等的直角三角形拼成“赵爽弦图” ， BFCGx， BGx+

27、x， BC2BG2+CG2， 故选：B 【点评】本题考查了正方形的性质，全等三角形的判定与性质，勾股定理，直角三角形的性质等知识， 熟练掌握勾股定理的应用是解题的关键 10如图，在正方形网格（每个小正方形的边长都是 1）中，若将ABC 沿 AD 的方向平移 AD 长，得 DEF（B、C 的对应点分别为 E、F） ，则 BE 长为（ ） A1 B2 C D3 【分析】直接根据题意画出平移后的三角形进而利用勾股定理得出 BE 的长 【解答】解：如图所示：BE 故选：C 【点评】此题主要考查了勾股定理以及坐标与图形的变化，正确得出对应点位置是解题关键 11如图，点 E 在正方形 ABCD 的边 AB

28、 上，若 EB1，EC2，那么正方形 ABCD 的面积为（ ） A B3 C D5 【分析】先根据正方形的性质得出B90，然后在 RtBCE 中，利用勾股定理得出 BC2，即可得出 正方形的面积 【解答】解：四边形 ABCD 是正方形， B90， BC2EC2EB222123， 正方形 ABCD 的面积BC23 故选：B 【点评】本题考查了勾股定理：在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的 平方即如果直角三角形的两条直角边长分别是 a，b，斜边长为 c，那么 a2+b2c2也考查了正方形的 性质 12如图，在四边形 ABCD 中，ADBC，D90，AD4，BC3分别以点

29、A，C 为圆心，大于AC 长为半径作弧，两弧交于点 E，作射线 BE 交 AD 于点 F，交 AC 于点 O若点 O 是 AC 的中点，则 CD 的长为（ ） A2 B4 C3 D 【分析】连接 FC，根据基本作图，可得 OE 垂直平分 AC，由垂直平分线的性质得出 AFFC再根据 ASA 证明FOABOC，那么 AFBC3，等量代换得到 FCAF3，利用线段的和差关系求出 FD ADAF1然后在直角FDC 中利用勾股定理求出 CD 的长 【解答】解：如图，连接 FC，则 AFFC ADBC， FAOBCO 在FOA 与BOC 中， ， FOABOC（ASA） ， AFBC3， FCAF3，F

30、DADAF431 在FDC 中，D90， CD2+DF2FC2， CD2+1232， CD2 故选：A 【点评】本题考查了作图基本作图，勾股定理，线段垂直平分线的判定与性质，全等三角形的判定与 性质，难度适中求出 CF 与 DF 是解题的关键 13下列四组数据中，不能作为直角三角形的三边长的是（ ） A6，8，10 B10，15，20 C5，12，13 D7，24，25 【分析】先求出两小边的平方和，再求出最长边的平方，看看是否相等即可 【解答】解：A62+82102， 以 6，8，10 为边能组成直角三角形，故本选项不符合题意； B102+152202， 以 10，15，20 为边不能组成直

31、角三角形，故本选项符合题意； C52+122132， 以 5，12，13 为边能组成直角三角形，故本选项不符合题意； D72+242252， 以 7，24，25 为边能组成直角三角形，故本选项不符合题意； 故选：B 【点评】本题考查了勾股定理的逆定理，注意：如果一个三角形的两边 a、b 的平方和等于第三边 c 的平 方，那么这个三角形是直角三角形 14勾股定理是人类最伟大的科学发现之一，在我国古算书周髀算经中早有记载如图，以直角三角 形的各边为边分别向外作正三角形， 再把较小的两张正三角形纸片按图的方式放置在最大正三角形内 若 知道图中阴影部分的面积，则一定能求出（ ） A直角三角形的面积 B

32、最大正三角形的面积 C较小两个正三角形重叠部分的面积 D最大正三角形与直角三角形的面积和 【分析】 设三个正三角形面积分别为 S1， S2， S3， （不妨设 S1S2S3） ， 由勾股定理可得 S1S2+S3， 由面积和差关系可求解 【解答】解：设三个正三角形面积分别为 S1，S2，S3， （不妨设 S1S2S3） ，两个小正三角形的重叠部 分的面积为 S4， S1S2+S3， S阴影S1（S2+S3S4）S1S2S3+S4S4， 故选：C 【点评】本题考查的是勾股定理，如果直角三角形的两条直角边长分别是 a，b，斜边长为 c，那么 a2+b2 c2 15在算法统宗中有一道“荡秋千”的问题：

33、 “平地秋千未起，踏板一尺离地送行二步与人齐，五尺 人高曾记仕女佳人争蹴，终朝笑语欢嬉良工高士素好奇，算出索长有几 ”此问题可理解为：如图， 有一架秋千， 当它静止时， 踏板离地距离 AB 长度为 1 尺 将它往前水平推送 10 尺时， 即 AC10 尺， 则此时秋千的踏板离地距离 AD 就和身高 5 尺的人一样高若运动过程中秋千的绳索始终拉得很直， 则绳索 OA 长为（ ） A13.5 尺 B14 尺 C14.5 尺 D15 尺 【分析】设绳索有 x 尺长，根据勾股定理列方程即可得到结论 【解答】解：设绳索有 x 尺长，则 102+（x+15）2x2， 解得：x14.5 故绳索长 14.5

34、尺 故选：C 【点评】本题考查勾股定理的应用，理解题意能力，关键是能构造出直角三角形，用勾股定理来解 16如图，某公园内的一块草坪是长方形 ABCD，已知 AB8m，BC6m，公园管理处为了方便群众，沿 AC 修了一条近道，一个人从 A 到 C 走 ABC 比直接走 AC 多走了（ ） A2 米 B4 米 C6 米 D8 米 【分析】根据勾股定理可得答案 【解答】解：由勾股定理，得 捷径 AC10（m） ， 多走了 8+6104（m） 故选：B 【点评】本题考查了勾股定理，利用勾股定理得出捷径的长是解题关键 17下列条件中，不能判断ABC（a、b、c 为三边，A、B、C 为三内角）为直角三角形

35、的是（ ） Aa21，b22，c23 Ba：b：c3：4：5 CA+BC DA：B：C3：4：5 【分析】 根据勾股定理的逆定理和三角形内角和， 可以判断各个选项中的条件是否可以构成直角三角形， 从而可以解答本题 【解答】解：当 a21，b22，c23 时， 则 a2+b2c2， 即ABC 是直角三角形，故选项 A 不符合题意； 当 a：b：c3：4：5 时，设 a3x，b4x，c5x， 则 a2+b2（3x）2+（4x）2（5x）2c2， 即ABC 是直角三角形，故选项 B 不符合题意； 当A+BC 时，则C90， 即ABC 是直角三角形，故选项 C 不符合题意； 当A：B：C3：4：5 时

36、，则最大的C18075， 即ABC 不是直角三角形，故选项 D 符合题意； 故选：D 【点评】本题考查勾股定理的逆定理、三角形内角和，解答本题的关键是明确题意，利用勾股定理的逆 定理解答 二填空题（共二填空题（共 10 小题）小题） 18如图，四边形 ABCD 中，ABCD，ABC60，ADBCCD4，点 M 是四边形 ABCD 内的一个 动点，满足AMD90，则点 M 到直线 BC 的距离的最小值为 32 【分析】 取 AD 的中点 O， 连接 OM， 过点 M 作 MEBC 交 BC 的延长线于 E， 过点 O 作 OFBC 于 F， 交 CD 于 G，则 OM+MEOF求出 OM，OF

37、即可解决问题 【解答】解：取 AD 的中点 O，连接 OM，过点 M 作 MEBC 交 BC 的延长线于 E，过点 O 作 OFBC 于 F，交 CD 于 G，则 OM+MEOF AMD90，AD4，OAOD， OMAD2， ABCD， GCFB60， DGOCGF30， ADBC， DABB60， ADCBCD120， DOG30DGO， DGDO2， CD4， CG2， OG2，GF，OF3， MEOFOM32， 当 O，M，E 共线时，ME 的值最小，最小值为 32 【点评】本题考查解直角三角形，垂线段最短，直角三角形斜边中线的性质等知识，解题的关键是学会 用转化的思想思考问题，属于中考

38、常考题型 19对角线互相垂直的四边形叫做“垂美”四边形，现有如图所示的“垂美”四边形 ABCD，对角线 AC、 BD 交于点 O若 AD2，BC4，则 AB2+CD2 20 【分析】根据垂直的定义和勾股定理解答即可 【解答】解：ACBD， AODAOBBOCCOD90， 由勾股定理得，AB2+CD2AO2+BO2+CO2+DO2， AD2+BC2AO2+DO2+BO2+CO2， AB2+CD2AD2+BC2， AD2，BC4， AB2+CD222+4220 故答案为：20 【点评】本题考查的是垂直的定义，勾股定理的应用，正确理解“垂美”四边形的定义、灵活运用勾股 定理是解题的关键 20如图 1

39、，四个全等的直角三角形围成一个大正方形，中间是个小正方形，这个图形是我国汉代赵爽在注 解周髀算经时给出的，人们称它为“赵爽弦图” 在此图形中连接四条线段得到如图 2 的图案，记阴 影部分的面积为 S1，空白部分的面积为 S2，大正方形的边长为 m，小正方形的边长为 n，若 S1S2，则 的值为 【分析】可设图 2 阴影直角三角形另一条直角边为 x，根据 S1S2，可得 2x2m2，则 xm，再根 据勾股定理得到关于 m，n 的方程，可求的值 【解答】解：设图 2 中阴影直角三角形另一条直角边为 x，依题意有 4x2m2， 解得 xm， 由勾股定理得（m）2+（n+m）2m2， m22mn2n2

40、0， 解得 m1（1）n（舍去） ，m2（1+）n， 则的值为 故答案为： 【点评】本题考查了勾股定理的证明，根据正方形的面积公式和三角形形的面积公式得出它们之间的关 系是解题的关键 21 九章算术是中国传统数学的重要著作之一，奠定了中国传统数学的基本框架如图所示是其中记载 的一道“折竹”问题： “今有竹高一丈，末折抵地，去根三尺，问折者高几何？”题意是：一根竹子原高 1 丈（1 丈10 尺） ，中部有一处折断，竹梢触地面处离竹根 3 尺，试问折断处离地面多高？答：折断处 离地面 4.55 尺高 【分析】根据题意结合勾股定理得出折断处离地面的高度即可 【解答】解：设折断处离地面 x 尺， 根据

41、题意可得：x2+32（10 x）2， 解得：x4.55 答：折断处离地面 4.55 尺 故答案为：4.55 【点评】此题主要考查了勾股定理的应用，根据题意正确应用勾股定理是解题关键 22如图，在ABC 中，已知 AB2，ADBC，垂足为 D，BD2CD若 E 是 AD 的中点，则 EC 1 【分析】设 AEEDx，CDy，根据勾股定理即可求出答案 【解答】解：设 AEEDx，CDy， BD2y， ADBC， ADBADC90， 在 RtABD 中， AB24x2+4y2， x2+y21， 在 RtCDE 中， EC2x2+y21 EC0 EC1 另解：依据 ADBC，BD2CD，E 是 AD

42、的中点， 即可得判定CDEBDA， 且相似比为 1：2， ， 即 CE1 故答案为：1 【点评】本题考查勾股定理，解题的关键是熟练运用勾股定理，本题属于基础题型 23如图，ABC 中，点 E 在边 AC 上，EBEA，A2CBE，CD 垂直于 BE 的延长线于点 D，BD8， AC11，则边 BC 的长为 4 【分析】延长 BD 到 F，使得 DFBD，根据等腰三角形的性质与判定，勾股定理即可求出答案 【解答】解：延长 BD 到 F，使得 DFBD， CDBF， BCF 是等腰三角形， BCCF， 过点 C 作 CHAB，交 BF 于点 H ABDCHD2CBD2F， HFHC， CHAB，

43、ABECHE，BAEECH， EHCE， EAEB， ACBH， BD8，AC11， DHBHBDACBD3， HFHC835， 在 RtCDH， 由勾股定理可知：CD4， 在 RtBCD 中， BC4， 故答案为：4 【点评】本题考查勾股定理，解题的关键是熟练运用等腰三角形的性质与判定，本题属于中等题型 24在 RtABC 中，C90，若 ABAC2，BC8，则 AB 的长是 17 【分析】在 RtABC 中，根据勾股定理列出方程即可求解 【解答】解：在 RtABC 中，C90，ABAC2，BC8， AC2+BC2AB2， 即（AB2）2+82AB2， 解得 AB17 故答案为：17 【点评

44、】 本题考查了勾股定理， 解答的关键是熟练掌握勾股定理的定义及其在直角三角形中的表示形式 25如图，已知边长为 2 的等边三角形 ABC 中，分别以点 A，C 为圆心，m 为半径作弧，两弧交于点 D， 连接 BD若 BD 的长为 2，则 m 的值为 2 或 2 【分析】由作图知，点 D 在 AC 的垂直平分线上，得到点 B 在 AC 的垂直平分线上，求得 BD 垂直平分 AC，设垂足为 E，得到 BE，当点 D、B 在 AC 的两侧时，如图，当点 D、B 在 AC 的同侧时，如图， 解直角三角形即可得到结论 【解答】解：由作图知，点 D 在 AC 的垂直平分线上， ABC 是等边三角形， 点

45、B 在 AC 的垂直平分线上， BD 垂直平分 AC， 设垂足为 E， ACAB2， BE， 当点 D、B 在 AC 的两侧时，如图， BD2， BEDE， ADAB2， m2； 当点 D、B 在 AC 的同侧时，如图， BD2， DE3， AD2， m2， 综上所述，m 的值为 2 或 2， 故答案为：2 或 2 【点评】本题考查了勾股定理，等边三角形的性质，线段垂直平分线的性质正确的作出图形是解题的 关键 26勘测队按实际需要构建了平面直角坐标系，并标示了 A，B，C 三地的坐标，数据如图（单位：km） 笔 直铁路经过 A，B 两地 （1）A，B 间的距离为 20 km； （2）计划修一条

46、从 C 到铁路 AB 的最短公路 l，并在 l 上建一个维修站 D，使 D 到 A，C 的距离相等， 则 C，D 间的距离为 13 km 【分析】 （1）由垂线段最短以及根据两点的纵坐标相同即可求出 AB 的长度； （2）根据 A、B、C 三点的坐标可求出 CE 与 AE 的长度，设 CDx，根据勾股定理即可求出 x 的值 【解答】解： （1）由 A、B 两点的纵坐标相同可知：ABx 轴， AB12（8）20； （2）过点 C 作 lAB 于点 E，连接 AC，作 AC 的垂直平分线交直线 l 于点 D， 由（1）可知：CE1（17）18， AE12， 设 CDx， ADCDx， 由勾股定理可

47、知：x2（18x）2+122， 解得：x13， CD13， 故答案为： （1）20； （2）13； 【点评】本题考查勾股定理，解题的关键是根据 A、B、C 三点的坐标求出相关线段的长度，本题属于中 等题型 27如图，AB 与 CD 相交于点 O，ABCD，AOC60，ACD+ABD210，则线段 AB，AC，BD 之间的等量关系式为 AB2AC2+BD2 【分析】过点 A 作 AECD，截取 AECD，连接 BE、DE，则四边形 ACDE 是平行四边形，得出 DE AC，ACDAED，证明ABE 为等边三角形得出 BEAB，求得BDE360（AED+ABD） EAB90，由勾股定理得出 BE2DE2+BD2，即可得出结果 【解答】解：过点 A 作 AECD，截取 AECD，连接 BE、DE，如图所示： 则四边形 ACDE 是平行四边形， DEAC，ACDAED， AOC60，ABCD， EAB60，CDAEAB， ABE 为等边三角形， BEAB， ACD+ABD210， AED+ABD210， BDE360（AED+ABD）EAB3602106090， BE2DE2+BD2， AB2AC2+BD2； 故答案为：AB2AC2+BD2 【点评】本题考查了勾股定理、平行四边形的判定与性质、等边三角形的判定与性质、平行线的性质、 四边形内角和等知识，熟练掌握平行四边形的性质