2021届上海市普陀区高考数学调研试卷（含答案解析）

《2021届上海市普陀区高考数学调研试卷（含答案解析）》由会员分享，可在线阅读，更多相关《2021届上海市普陀区高考数学调研试卷（含答案解析）（16页珍藏版）》请在七七文库上搜索。

1、2021 年上海市普陀区高考数学调研试卷（年上海市普陀区高考数学调研试卷（3 月份）月份） 一、填空题（一、填空题（60 分）分） 1已知集合 U2，1，0，1，2，3，A1，0，1，B1，2，则U（AB） 2已知 sinx，x（，），则 cos（x） 3已知一个关于 x，y 的二元线性方程组的增广矩阵是，则 x+y 4已知复数 z（i 为虚数单位）， 表示 z 的共轭复数，则 z 5已知直线 l 的参数方程是（x，yR），则直线 l 的倾斜角的大小为 6高三某位同学参加物理、化学、政治科目的等级考，已知这位同学在物理、化学、政治科目考试中得 A+ 概率分别为， 这三门科目考试成绩互不影响，

2、则这位考生至少得 2 个 A+的概率为 7在某次数学测验中，6 位学生的成绩如下：78，85，a，82，69，80，他们得平均成绩为 80，他们成绩 的中位数为 8下面是某算法的程序框图，则程序运行后输出的结果为 9已知圆锥的底面半径为 1，母线长为 3，则该圆锥内半径最大的球的表面积为 10已知实数 m1，实数 x、y 满足不等式组，若目标函数 zx+my 的最大值等于 10，则 m 11设 Pn（xn，yn）是直线 3x+y（nN*）与圆 x2+y25 在第四象限的交点，则极限 12已知向量 ， 的夹角为锐角，且满足| |、| |，若对任意的（x，y）（x，y）|x +y |1， xy0，

3、都有|x+y|1 成立，则 的最小值为 二、选择题（满分二、选择题（满分 20 分）分） 13如图，一个空间几何体的主视图、左视图、俯视图均为全等的等腰直角三角形，如果直角三角形的直 角边长都为 1，那么这个几何体的体积是（ ） A B C D1 14 点 O 是三角形 ABC 所在平面内的一点， 满足， 则点 O 是三角形 ABC 的 （ ） A内心 B外心 C重心 D垂心 15 著名的波那契列an： 1， 1， 2， 3， 5， 8， ， 满足 a1a21， an+2an+1+an（nN*） ， 那么 1+a3+a5+a7+a9+ +a2021是斐波那契数列中的（ ） A第 2020 项

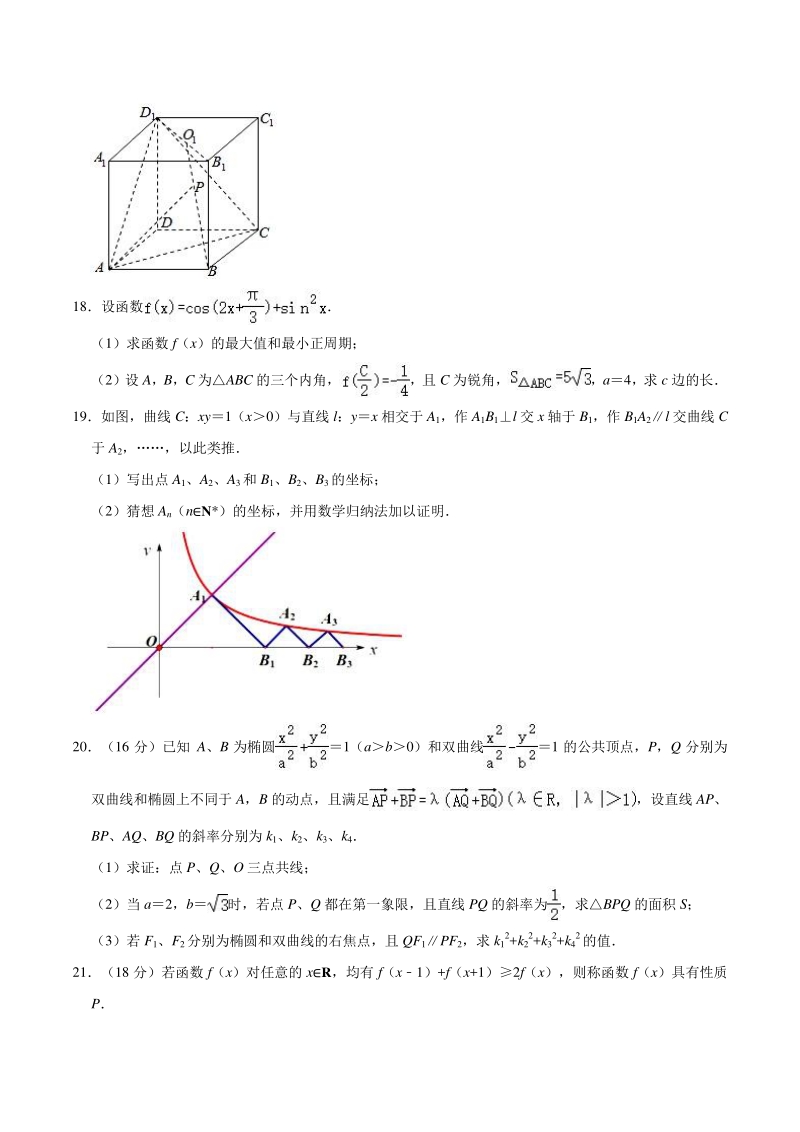
4、B第 2021 项 C第 2022 项 D第 2023 项 16已知 xR，符号表示不超过 x 的最大整数，若函数 f（x）a（x0）有且仅有 4 个零点，则实 数 a 的取值范围是（ ） A B C D 三、解答题（满分三、解答题（满分 76 分）分） 17如图，在直四棱柱 ABCDA1B1C1D1中，底面 ABCD 为菱形，AC4，BD2，且侧棱 AA13其中 O1为 A1C1与 B1D1的交点 （1）求点 B1到平面 D1AC 的距离； （2）在线段 BO1上，是否存在一个点 P，使得直线 AP 与 CD1垂直？若存在，求出线段 BP 的长；若不 存在，请说明理由 18设函数 （1）求函

5、数 f（x）的最大值和最小正周期； （2）设 A，B，C 为ABC 的三个内角，且 C 为锐角，a4，求 c 边的长 19如图，曲线 C：xy1（x0）与直线 l：yx 相交于 A1，作 A1B1l 交 x 轴于 B1，作 B1A2l 交曲线 C 于 A2，以此类推 （1）写出点 A1、A2、A3和 B1、B2、B3的坐标； （2）猜想 An（nN*）的坐标，并用数学归纳法加以证明 20（16 分）已知 A、B 为椭圆1（ab0）和双曲线1 的公共顶点，P，Q 分别为 双曲线和椭圆上不同于 A，B 的动点，且满足，设直线 AP、 BP、AQ、BQ 的斜率分别为 k1、k2、k3、k4 （1）求

6、证：点 P、Q、O 三点共线； （2）当 a2，b时，若点 P、Q 都在第一象限，且直线 PQ 的斜率为，求BPQ 的面积 S； （3）若 F1、F2分别为椭圆和双曲线的右焦点，且 QF1PF2，求 k12+k22+k32+k42的值 21（18 分）若函数 f（x）对任意的 xR，均有 f（x1）+f（x+1）2f（x），则称函数 f（x）具有性质 P （1）判断下面两个函数是否具有性质 P，并说明理由； y3x；yx3； （2）若函数 g（x），试判断 g（x）是否具有性质 P，并说明理由； （3）若函数 f（x）具有性质 P，且 f（0）f（n）0（n2，nN*）求证：对任意 1kn1，

7、kN*， 均有 f（k）0 参考答案参考答案 一、填空题（本大题满分一、填空题（本大题满分 60 分）本大题共有分）本大题共有 12 小题要求直接将结果填写在答题纸对应的空格中，小题要求直接将结果填写在答题纸对应的空格中，1-6 每个每个 空格填对得空格填对得 4 分，分，7-12 每个空格填对得每个空格填对得 6 分填错或不填在正确的位置一律得零分）分填错或不填在正确的位置一律得零分） 1已知集合 U2，1，0，1，2，3，A1，0，1，B1，2，则U（AB） 2，3 解：U2，1，0，1，2，3，A1，0，1，B1，2， AB1，0，1，2，U（AB）2，3 故答案为：2，3 2已知 si

8、nx，x（，），则 cos（x） 解：因为 sinx，x（，）， 可得 cosx， 所以 cos（x）cosx 故答案为： 3已知一个关于 x，y 的二元线性方程组的增广矩阵是，则 x+y 6 【解答】解由二元线性方程组的增广矩阵， 可得到二元线性方程组的表达式， 解得， 所以 x+y6 故答案为 6 4已知复数 z（i 为虚数单位）， 表示 z 的共轭复数，则 z 1 解：z， z 故答案为：1 5已知直线 l 的参数方程是（x，yR），则直线 l 的倾斜角的大小为 110 解：直线 l 的参数方程是（x，yR）， 转换为标准式为（t 为参数）， 所以直线的倾斜角为 110， 故答案为：11

9、0 6高三某位同学参加物理、化学、政治科目的等级考，已知这位同学在物理、化学、政治科目考试中得 A+ 概率分别为， 这三门科目考试成绩互不影响， 则这位考生至少得2个A+的概率为 解：设这位同学在物理、化学、政治科目考试中得 A+的事件分别为 A，B，C， 则 P（A），P（B），P（C）， 这位考生至少得 2 个 A+的概率为： P（AB ）+P（A C）+P（）+P（ABC） P（A）P（B）P（ ）+P（A）P（ ）P（C）+P（ ）P（B）P（C）+P（A）P（B）P（C） +（1） 故答案为： 7在某次数学测验中，6 位学生的成绩如下：78，85，a，82，69，80，他们得平均成绩

10、为 80，他们成绩 的中位数为 81 解：因为 6 位学生的成绩如下：78，85，a，82，69，80，他们得平均成绩为 80， 所以 78+85+a+82+69+80680，解得 a86， 则将 6 位学生的成绩从小到大排列为：69，78，80，82，85，86， 所以他们成绩的中位数为 故答案为：81 8下面是某算法的程序框图，则程序运行后输出的结果为 14 解：由程序框图知：第一次循环 n1，S1+10； 第二次循环 n2，S0+1+23； 第三次循环 n3，S31+35； 第四次循环 n4，S5+1+410； 第五次循环 n5，S101+514， 满足条件 S13，跳出循环，输出 S

11、的值为 14 故答案为：14 9已知圆锥的底面半径为 1，母线长为 3，则该圆锥内半径最大的球的表面积为 2 解：设内切球的半径为 r，则利用轴截面，根据等面积可得2（3+3+2）r， r， 该圆锥内切球的表面积为 4r22， 故答案为：2 10已知实数 m1，实数 x、y 满足不等式组，若目标函数 zx+my 的最大值等于 10，则 m 2 解：由约束条件作出可行域如图内的整数点（含边界线上的整数点）， 联立，解得 A（3，3）， B（，）， 化目标函数 zx+my 为 yx+z， 由图可知，当直线 yx+z 过 B 时，直线在 y 轴上的截距最大，但 B 不是整数点， 因为：0 x3，0y

12、， 故当 y4，x2 时，z 有最大值为 2+4m10， 即 m2 故答案为：2 11设 Pn（xn，yn）是直线 3x+y（nN*）与圆 x2+y25 在第四象限的交点，则极限 解：当 n+时，1， 直线 3x+y（nN*）与圆 x2+y25 在第四象限的交点无限靠近 A（1，2）， 而可看作点 Pn（xn，yn）与 A（1，2）连线的斜率， 其值会无限接近圆 x2+y25 在点 A（1，1）处的切线的斜率， 其斜率为 kOA2， 故答案为： 12已知向量 ， 的夹角为锐角，且满足| |、| |，若对任意的（x，y）（x，y）|x +y |1， xy0，都有|x+y|1 成立，则 的最小值为

13、 解：因为|x|1，且| | 、| |， 则|x|2x 1（x+y）2恒成立， 所以1恒成立， 只需，又 1， 当且仅当 18x22y2时取等号，此时 1 的最大值为， 所以，即的最小值为， 故答案为： 二、选择题（本大题满分二、选择题（本大题满分 20 分）本大题共有分）本大题共有 4 题，每题有且只有一个结论是正确的，必须把正确结论的代题，每题有且只有一个结论是正确的，必须把正确结论的代 号涂在答题纸相应的位置上每题选对得号涂在答题纸相应的位置上每题选对得 5 分，不选、选错或选出的代号超过一个一律得零分分，不选、选错或选出的代号超过一个一律得零分. 13如图，一个空间几何体的主视图、左视

14、图、俯视图均为全等的等腰直角三角形，如果直角三角形的直 角边长都为 1，那么这个几何体的体积是（ ） A B C D1 解：根据三视图，可知该几何体是三棱锥，可由正方体截得， 为正方体中的三棱锥 PABC，正方体棱长为 1 几何体的体积为： 故选：C 14 点 O 是三角形 ABC 所在平面内的一点， 满足， 则点 O 是三角形 ABC 的 （ ） A内心 B外心 C重心 D垂心 解：，（）0 ， 0，可得 因此，点 O 在 AC 边上的高 BE 上， 同理可得：O 点在 BC 边上的高 AF 和 AB 边上的高 CD 上 点 O 是ABC 三条高线的交点 因此，点 O 是ABC 的垂心 故选

15、：D 15 著名的波那契列an： 1， 1， 2， 3， 5， 8， ， 满足 a1a21， an+2an+1+an（nN*） ， 那么 1+a3+a5+a7+a9+ +a2021是斐波那契数列中的（ ） A第 2020 项 B第 2021 项 C第 2022 项 D第 2023 项 解：因为 a1a21， 所以 1+a3+a5+a7+a9+a2021 a2+a3+a5+a7+a9+a2021 a4+a5+a7+a9+a2021 a6+a7+a9+a2021 a2020+a2021 a2022， 故选：C 16已知 xR，符号表示不超过 x 的最大整数，若函数 f（x）a（x0）有且仅有 4

16、个零点，则实 数 a 的取值范围是（ ） A B C D 解：由 f（x）a0 得a， 设 g（x）， 则当 0 x1，x0，此时 g（x）0， 当 1x2，x1，此时 g（x），此时 g（x）1， 当 2x3，x2，此时 g（x），此时 g（x）1， 当 3x4，x3，此时 g（x），此时 g（x）1， 当 4x5，x4，此时 g（x），此时 g（x）1， 当 5x6，x5，此时 g（x），此时 g（x）1， 当 6x7，x6，此时 g（x），此时 g（x）1， 作出函数 g（x）的图象， 要使 f（x）a 有且仅有 4 个零点， 即函数 g（x）a 有且仅有 4 个零点， 则由图象可知 a

17、或a， 故选：B 三、 解答题 （本大题满分三、 解答题 （本大题满分 76 分） 本大题共有题解答下列各题必须在答题纸规定的方框内写出必要的步骤。 ）分） 本大题共有题解答下列各题必须在答题纸规定的方框内写出必要的步骤。 ） 17如图，在直四棱柱 ABCDA1B1C1D1中，底面 ABCD 为菱形，AC4，BD2，且侧棱 AA13其中 O1为 A1C1与 B1D1的交点 （1）求点 B1到平面 D1AC 的距离； （2）在线段 BO1上，是否存在一个点 P，使得直线 AP 与 CD1垂直？若存在，求出线段 BP 的长；若不 存在，请说明理由 【解答】（本题满分 14 分） 本题共 2 个小题

18、，每小题 解：（1）由于菱形的对角线互相垂直平分， 故以 AC 与 BD 的交点 O 为原点，以射线 OA、OB、OO1分别为 x、y、z 轴，建立空间直角坐标系 由已知条件，相关点的坐标为 A（2，0，0），B（0，1，0），C（2，0，0），O1（0，0，3），B1（0， 1，3），D1（0，1，3） 设平面 D1AC 的法向量为 ， 由， 得， 令 z1，则 因， 故点 B1到平面 D1AC 的距离为 （2）设， 则由， 得 又， 故当时， 于是，在线段 BO1上存在点 P，使得 APCD1；此时 18设函数 （1）求函数 f（x）的最大值和最小正周期； （2）设 A，B，C 为ABC

19、的三个内角，且 C 为锐角，a4，求 c 边的长 解：（1）+ 所以； 当时， （2）由得，； 所以，C 为锐角，故； ，所以 b5 所以：c2a2+b22abcosC 21 故 19如图，曲线 C：xy1（x0）与直线 l：yx 相交于 A1，作 A1B1l 交 x 轴于 B1，作 B1A2l 交曲线 C 于 A2，以此类推 （1）写出点 A1、A2、A3和 B1、B2、B3的坐标； （2）猜想 An（nN*）的坐标，并用数学归纳法加以证明 解：（1）根据题意，由，求得 A1（1，1）， 由，求得 B1（2，0）， 由，求得 A2（+1，1）， 由，求得 B2（2，0）， 由，求得 A3（+

20、，）， 由，求得 B3（2，0） （2）由（1）猜想 An（nN*）的坐标为 An（+， ）， 设 An（xn，yn），An1（xn1，yn1），则直线的方程为 yyn 1x+xn1， 令 y0，解得 Bn1（yn1+xn1，0）， 因为直线 AnBn1的斜率为 1，即 1， 所以 yn+yn1xnxn1，整理得 +xnxn1； 用数学归纳法证明 An的坐标如下： 当 n1 时，验证成立； 当 nk 时，假设成立，即 Ak（+，）， 由递推关系得+xk+1（+）， 解得 xk+1+ ； 综上知，An（+， ） 20（16 分）已知 A、B 为椭圆1（ab0）和双曲线1 的公共顶点，P，Q 分别

21、为 双曲线和椭圆上不同于 A，B 的动点，且满足，设直线 AP、 BP、AQ、BQ 的斜率分别为 k1、k2、k3、k4 （1）求证：点 P、Q、O 三点共线； （2）当 a2，b时，若点 P、Q 都在第一象限，且直线 PQ 的斜率为，求BPQ 的面积 S； （3）若 F1、F2分别为椭圆和双曲线的右焦点，且 QF1PF2，求 k12+k22+k32+k42的值 解： （1）证明：因为 A，B 为椭圆与双曲线的公共点，P，Q 分别为双曲线和椭圆上不同于 A，B 的动点， 又因为+（+）， 所以 22，即 ， 所以点 P，Q，O 三点共线 （2）设 P（x1，y1），Q（x2，y2）， 直线 P

22、Q 的方程为 yx， 联立，解得 x，y， 所以 P（，）， 同理，解得 x，y， 解得 Q（，）， 则|PQ|3， 又因为 a2，b， 联立，解得 B（2，0）， 所以点 B 到直线 PQ 的距离 d， 则 Sd|PQ| （3）因为， 所以， 则， 因为 QF1PF2， 所以|OF1|OF2|， 所以 2， 所以， 所以（k1+k2）24 4， 同理（k3+k4）24， 而 k1k2 ， 又 x12a2+ y 1 2， 所以 k1k2， 同理 k1k4， 所以 k12+k22+k32+k428 21（18 分）若函数 f（x）对任意的 xR，均有 f（x1）+f（x+1）2f（x），则称函数

23、 f（x）具有性质 P （1）判断下面两个函数是否具有性质 P，并说明理由； y3x；yx3； （2）若函数 g（x），试判断 g（x）是否具有性质 P，并说明理由； （3）若函数 f（x）具有性质 P，且 f（0）f（n）0（n2，nN*）求证：对任意 1kn1，kN*， 均有 f（k）0 解：（1）f（x1）+f（x+1）2f（x）3x1+3x+123x3x（）0，故具有性质 P； 不具有性质 P，如 x1 时，f（x1）+f（x+1）f（2）+f（0）8，而 2f（1）2，不 满足不等式， （2）1当 x 为有理数时，具有性质 P，理由如下： f（x1）+f（x+1）2f（x）（x1）2

24、+（x+1）22x2n（x1+x+12x）20， 2当 x 为无理数时，具有性质 P，理由如下： f（x1）+f（x+1）2f（x）（x1）2+（x+1）22x220， 综上可知 g（x）具有性质 P （3）证明：假设 f（x）为 f（1），f（2），f（n1）中第一个大于 0 的值，则 f（k）f（k1） 0， 因为函数 f（x）具有性质 P，所以 f（n+1）f（n）f（n）f（n1）， 所以 f（n+1）f（n）f（n）f（n1）f（k）f（k1）o， 所以 f（n）f（n）f（n1）+f（n1f（n2）+f（1）0， 与 f（n）0 矛盾，所以假设错误，原命题正确， 即对于任意的 1kn1，kN*，均有 f（k）0