电工技能培训专题-电路分析基础-瞬态电路的分析

《电工技能培训专题-电路分析基础-瞬态电路的分析》由会员分享，可在线阅读，更多相关《电工技能培训专题-电路分析基础-瞬态电路的分析（105页珍藏版）》请在七七文库上搜索。

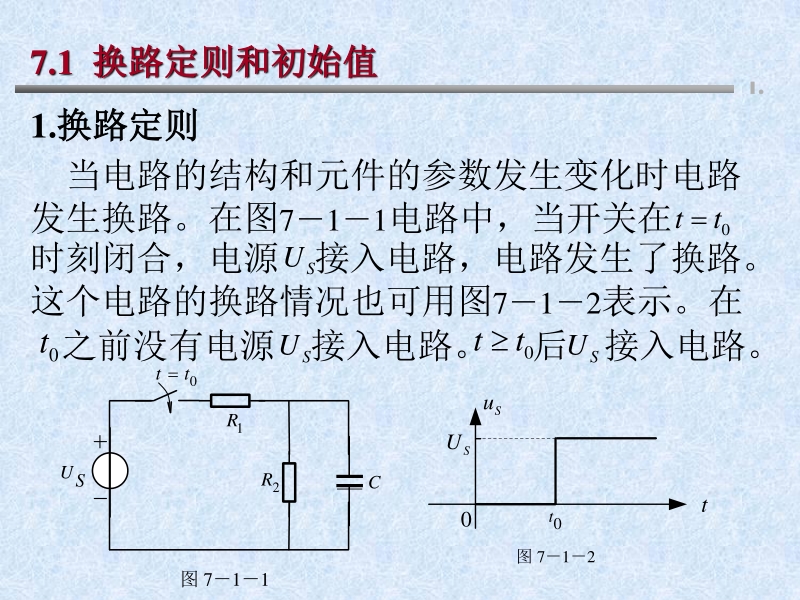
1、 7.1 换路定则和初始值换路定则和初始值 7.2 一阶电路的零输入响应一阶电路的零输入响应 7.3 一阶电路的零状态响应一阶电路的零状态响应 第七章第七章 瞬态电路的分析瞬态电路的分析 7.5 求解一阶电路的三要素公式求解一阶电路的三要素公式 7.4 一阶电路的全响应一阶电路的全响应 7.6 微分电路与积分电路微分电路与积分电路 7.7二阶电路的零输入响应二阶电路的零输入响应 7. 8 二阶电路的零状态响应二阶电路的零状态响应 1.1. 1.换路定则换路定则 7.1 换路定则和初始值换路定则和初始值 当电路的结构和元件的参数发生变化时电路 发生换路。在图711电路中，当开关在 0 tt 时刻

2、闭合，电源 接入电路，电路发生了换路。 这个电路的换路情况也可用图712表示。在 S U 之前没有电源 接入电路。 后 接入电路。 0 t S U 0 tt S U 图 711 0 tt 1 R 2 R C U S 0 t S u 0 t 图 712 S U 1.1. 7.1 换路定则换路定则 若电路在 时刻换路，换路前瞬间为 ，换 路后瞬间为 ，电容电压和电感电流换路时保 持不变即 0t 0 0 )0()0( cc uu (0 )(0 ) LL ii （7-1-1） 或者用电路的电荷和电感的磁链表示 (0 )(0 ) cc qq (0 )(0 ) LL （7-1-2） 式711和式712称为

3、换路定则。 1.1. 7.1 换路定则换路定则 换路定则表明 电容电流为有限值时，电容上的电荷和 电压在换路瞬间是连续的而不突变。 电感电压为有限值时，电感中的磁链和 电流在换路瞬间是连续的而不突变。 )0()0( cc uu (0 )(0 ) LL ii 1.1. 2、电路的初始值计算、电路的初始值计算 电路在 时刻发生换路，换路前储能元件 电容电压 、电感电流 称为初始状态。 0t (0 ) C u (0 ) L i (0 ) L i (0 ) C u (0 ) R i (0 ) L u 和各阶导数的值如 dt di)0( 、 等，称为初始 dt du)0( 值或初始条件。初始值通过换路前

4、瞬间 (0 ) C u (0 ) L i 、 值和换路定则来求得。 初始状态初始状态 换路后瞬间各电量值如 、 、 、 初始值初始值 1.1. 2、电路的初始值计算、电路的初始值计算 （1）先求出 (0 ) C u 、 值。 (0 ) L i （2）利用换路定则求出 、 的值， (0 ) L i (0 ) C u (0 )(0 ) ll ii (0 )(0 ) cc uu ， 。 （3）画出 时刻的等效电路， 用电流源 0t (0 ) L i 替代， 用电压源替代，求出待求的 (0 ) C u (0 ) L i (0 ) C u 、 、 、 等值。 (0 ) R i (0 ) L u 1.1.

5、 例例711电路的初始值计算电路的初始值计算 电路如图713（a）所示,开关闭合之 前电路已处于稳定状态，开关在 时刻闭合， 求 、 和 。 0t (0 ) C u (0 )i (0 ) R u 0t R u US C u i (a) (0 ) R u US (0 )i (b) (0 ) C u 图 713 1.1. 例例711 解：解： 0t 开关打开，电路处于稳定状态， (0 )0V C u 时根据换路定则 0t (0 )(0 )0V CC uu 0t 时的等效电路如图713（b）所示 (0 )0Ai (0 ) S R uU 0t R u US C u i (a) (0 ) R u US

6、(0 )i (b) (0 ) C u 图 713 1.1. 例例712 电路如图（a）所示，电路处于稳态，当 时开关打开，求开关打开瞬间 0t (0 ) R i (0 ) C i (0 ) L i (0 ) L u (0 ) L di dt 、 、 、 和 的值。 1.1. 例例712 解：解： 0t 时开关闭合，电路已处于稳态，等效 电路如图（b）所示，求 和 (0 ) L i (0 ) c u 15 (0 )5V 2 13 C u 55 (0 )A 2 13 L i 据换路定则 5 (0 )(0 )A 3 LL ii 5 (0 )(0 )V 3 cc uu 1.1. 例例712 当 时开关

7、打开，等效电路如图（c）所示 0t 5 (0 )(0 )A 3 CL ii (0 )(0 )(0 )0A RCL iii (0 )(0 )(0 ) 3(0 ) 1 LCCL uuii 55 ( 5)5V 33 0 (0 )(0 )5 A 1 S 5 LLL t didiu dtdtL 1.1. 7.2 一阶电路的零输入响应一阶电路的零输入响应 含有一个独立的动态元件的电路，描述这 样电路的方程是一阶微分方程，该电路称为一 阶电路。 含有一个电容元件或一个电感元件的电路 都是一阶电路。 没有外加电源，由电容和电感元件储存的 能量激励电路产生的响应称为零输入响应。 1.1. 721 RC电路的零输

8、入的响应电路的零输入的响应 图示电路，已知电容在开关闭合前已储存 有电荷，开关在 时刻闭合，电容电压 0t 0 (0 ) C uU ，可以推测电路的工作过程。 0 (0 )(0 ) CC uuU 随后电容储存的电荷通过电阻 放电。 t 电容放电结束，此时 ( )0, ( )0,( )0 CR uiu 换路时 换路瞬间电容电压保持不变， 1.1. 当开关闭合后 0t ，由KVL可得 ( )( ) CR utu t ( ) ( )( ), ( ) c R du t utRi t i tC dt 又 ，代入上式可得 ( ) ( )0 C C dut RCut dt （721） 721 RC电路的零输

9、入的响应电路的零输入的响应 分析电容通过电阻的 放电规律 1.1. 用经典法解微分方程，首先确定初始值 0 (0 )(0 ) CC uuU 齐次微分方程的通解 ( ) st c u tAe （722） 将式（722）代入（721）可得 0 stst RCSAeAe 得到特征方程 10RCS 721 RC电路的零输入的响应电路的零输入的响应 1.1. 将特征根 1 S RC 代入式（722）得方程的通解 ( ) t RC C utAe 在用初始值确定待定系数A 0 0 (0 ) C uAeU 0 AU 0 ( ) t RC C utU e ( )(0 ) t cc u tUe 或写成 （723）

10、 721 RC电路的零输入的响应电路的零输入的响应 1.1. 其中 RC 称为电路的时间常数 电路中的电流 0 ( ) t c RC duU i tCe dtR 或写成 ( )(0 ) t i tie （724） 由式（723），（724）可归纳出求解 一阶电路零输入响应的公式 ( )(0 ) t y tye 721 RC电路的零输入的响应电路的零输入的响应 1.1. 721 RC电路的零输入的响应电路的零输入的响应 为 后任一瞬时电路的响应； (0 )y 0t 为 时刻的响应值； ( )y t0t 为一阶电路的时间常数。 ( )(0 ) t y tye 1.1. 721 RC电路的零输入的响

11、应电路的零输入的响应 从曲线的整个时序看出电路经历了三个工作状 态， 电路处于原稳态 ； t 0 0 U 0 U R ( ) C ti( ) C tu ( ) C tu ( ) C ti 图 732 0t 0 (0 ), (0 )0 cc uU i 0t 电路进入瞬态（过度过程）， 0 0 ( ),( ) tt CC U utU eite R ；当 时，电路达到新稳态 t ( )0, ( )0 cc ui 电路响应 ( ) C ut 和 的波形 ( ) C i t 1.1. 722 RL电路的零输入响应电路的零输入响应 在RL电路中，没有外部激励源作用只是由 电感初始储能 引起的响应，称为RL

12、电路的 零输入响应。图（a)所示电路，开关打开之前 电路处于稳定状态 时开关打开，等 效电路如图 (b)所示，根据换路定则 (0 ) L i 0 (0 ),0 L iI t 1.1. 722 RL电路的零输入响应电路的零输入响应 由KVL得 代入上式得一阶齐次微分方程 又 0 (0 )(0 ) LL iiI ( )( ) RL utu t ( ), ( ) L RL di utiRutL dt ( )0 L L diR i t dtL 特征方程 0 R S L 1.1. 722 RL电路的零输入响应电路的零输入响应 特征根 R S L 微分方程齐次解 st L iAe 0 (0 ) R L L

13、 iAeA 0 (0 ) L AiI 0 ( ) R t L L i tI e ( )(0 ) t LL i tie L R 由初始条件确定A 所以 或表示为 （7-2-1） 其中时间系数 1.1. 722 RL电路的零输入响应电路的零输入响应 式（7-2-1）符合一阶电路的零输入响应公式 ( )(0 ) t y tye 电感电压和电阻电压分别为 0 ( ) ( ) t L L di t u tLRI e dt 0 ( )( ) t RL utRi tRI e ( ),( ),( ) LRL i t u t u t 曲线如图所示。 1.1. 722 RL电路的零输入响应电路的零输入响应 的瞬态

14、曲线都以指数衰减规律 变化。 ( ),( ),( ) LRL i t u tu t 1.1. 723 一阶电路的时间常数一阶电路的时间常数 在解微分方程时求出的特征根 1 S S ，称为 电路的固有频率或自然频率。 RC R的单位用欧姆，C的单位用法拉，的单位为秒。 L GL R 称为时间常数。 其中L单位用亨利，R单位用欧姆， 的单位为秒。 在RL单路中， 与 都是电路的 固有参数，反映了电路的特性。 在RC回路中 1.1. 723 一阶电路的时间常数一阶电路的时间常数 值的大小决定了指数函数 的衰减速度， t e 越大，衰减越慢， 越小，衰减越快。图 给出了三种不同时间常数下 的变化曲线。

15、 c u 1.1. 723 一阶电路的时间常数一阶电路的时间常数 RC 越大说明 R或C越大。从物理概念上 讲，如C一定，电阻R愈大，则放电电流的起始 值就愈小，放电所需时间长，放电速度慢；如 ， R一定，则放电电流的起始值一定，C愈大，电 容起始储存的电荷愈多，放电需要的时间就愈 长。 t 从理论上讲当 时按指数规律变化的电量 衰减到零，电路的放电结束，瞬态持续的时间 是0，实际中取 5），电量已衰减到起 (4t 始值的 1.8% 0.7%，认为放电完毕，瞬态结束。 1.1. 723 一阶电路的时间常数一阶电路的时间常数 零输入响应 0 ( )() t y ty te ，当 时 ， t 1

16、0 ( ) 0.368 () y e y t ， 即当电量下降到初始值的 36.8% 时，时间t对应的值是 ，如图726所示，如 果作t=0 时曲线的切线，切线与t 轴的交点在 t 处。所以可由电路响应曲线用作图方法求 出时间常数 。 1.1. 73 一阶电路的零状态响应一阶电路的零状态响应 电路的初始状态为零由外加激励引起的 响应称为零状态响应。 731 RC电路的零状态响应电路的零状态响应 732 RL电路的零状态响应电路的零状态响应 1.1. 731 RC电路的零状态响应电路的零状态响应 在图中电容的初始储能为零 ，开关 在t=0时闭合， 时 ，此刻 (0 )0 c u 0t (0 )(

17、0 )0 cc uu 电容相当于短路，随后电源给电容充电,分析 0t 时的电路,列写KVL方程 S U ( ) C tu R 0t ( ) C it C sRC uuu 1.1. 731 RC电路的零状态响应电路的零状态响应 元件的约束关系 ( ) ( ), ( ) c CRC du t itCuRit dt 代入上式，得 ( ) ( ) c cS du t RCu tU dt 整理后，得 ( )1 ( ) cS C du tU ut dtRCRC （731） 1.1. 731 RC电路的零状态响应电路的零状态响应 式（731）是非齐次一阶微分方程，方程 的解包括非齐次方程的特解 和齐次方程的

18、 ( ) cp ut 解 即 ( ) ch ut ( )( )( ) cchcp u tutut 齐次方程的解 ( ) t RC ch utAe 方程的特解与激励同形式 , cp uBB 为常数 1.1. 731 RC电路的零状态响应电路的零状态响应 代入原方程，得 S BU cpS uU 原方程（7-3-1）的通解 ( )( )( ) cchcp u tutut t RC S AeU 再用初始值确定待定系数A 0 (0 )0 cS uAeU S AU 方程的解 ( ) t RC cSS u tU eU (1) t RC S Ue （732） 1.1. 731 RC电路的零状态响应电路的零状态

19、响应 回路电流 ( ) ( )(1) t C RC cS dutd i tCCUe dtdt t S RC U e R ( ) c u t ( ) c i t 和 的曲线如图所示，在 时C充电， 0t 从0开始指数上升， ( ) c u tt ( ) cS uU 时， 达到稳态。 ( ) c i t S U R 从 开始指数下降， t 时 ( )0 c i 。 1.1. 732 RL电路的零状态响应电路的零状态响应 图示电路 , 时合上开关,电源 接入电路,分析电路的过度过程如下.： (0 )0 L i 0t 当 时 0t (0 )(0 ) LL ii 1.1. 732 RL电路的零状态响应电

20、路的零状态响应 ( ) ( ) L LS di t LRi tU dt 时由KVL可列写出微分方程 0t (733) 方程解 1 ( )( ) LLtLp iitit (734) 齐次解 ( ) R t L Lh itAe （735） 1.1. 732 RL电路的零状态响应电路的零状态响应 特解 LP iB 代入方程式（733），得 S U B R S LP U i R 代入式（734）得 1 ( )( ) LLtLp iitit R t S L U Ae R 1.1. 732 RL电路的零状态响应电路的零状态响应 由初始条件可求得 S U A R ( ) R t SS L L UU i te

21、 RR 原方程的解 (1) R t S L U e R （736） ( ) ( ) R t c L LS di t u tLU e dt 1.1. 732 RL电路的零状态响应电路的零状态响应 零状态的响应曲线如图所示， 和 ( ) L i t ( ) L u t 按指数规律变化。 电流初始值 随着电源给电感充电 (0 )0 L i ( ) L i t 指数上升， ( ) L u t 指数下降，当 t 时，过度过程结束，电路达到新的稳态， 电感等效成短路， ( ) S L U i R ( )0 L u ， 。 1.1. 732 RL电路的零状态响应电路的零状态响应 由式（732）和（736）可

22、以总结出，求 解一阶电路零状态响应 和 的公式 ( ) C ut( ) L i t ( )( )(1) t y tye ( )y t为 后，任一瞬时电容电压 或电感电 0t ( ) C ut 流 ( ) L i t； ( )y t 为 时刻的电容电压 或电感电流 ( ) C ut ( ) L i t 的终值； 为一阶电路的时间常数。 1.1. 74 一阶电路的全响应一阶电路的全响应 一阶电路换路后由外部激励和初始储能共 同作用引起的响应， 称为一阶电路的全响应。 图示电路，电路初始储能 0 (0 ), 0 c uUt 时开关闭合，分析 0t 的情况。 初始值 C u R 0t S U 0 (0

23、 )(0 ) cc uuU 列写电路的微分方程 ( ) ( ) c cS du t RCu tU dt （741） 1.1. 74 一阶电路的全响应一阶电路的全响应 解这个初始值不为零的非齐次微分方程， 可得电路的全响应为齐次解+特解 即 ( )( )( ) cchcp u tutut 特解 ( ) cp utB 代入式（741） S BU cpS uU 齐次解 ( ) t RC ch utAe 全解 ( ) t RC cS u tAeU 1.1. 74 一阶电路的全响应一阶电路的全响应 代入初始条件确定A 0 (0 ) cS uA UU 0S AUU 电路的全响应 0 ( )() t RC

24、cSS u tUUeU （742） 响应曲线如图所示 1.1. 74 一阶电路的全响应一阶电路的全响应 0 () t RC S UUe S U 加激励同形式。 全响应自由响应强迫响应 自由响应 0 () t RC S UUe ，当 时，该响应分量 为零，所以也叫瞬态响应。当激励为直流或正弦 周期信号时，与激励同形式的强迫响应叫稳定响 应。因此 t 全响应瞬态响应稳态响应 是强迫响应，是由外加激励引起的，与外 是自由响应，描述电路的瞬态程； 1.1. 将全响应重新组合为 0 ( )(1) tt RCRC cS u tU eUe （743） 其中 是电路的零输入响应， 0 t RC U e (1)

25、 t RC S Ue 是零状态响应，响应曲线 如图所示。 全响应零输入响应零状态响应 74 一阶电路的全响应一阶电路的全响应 所以 1.1. 74 一阶电路的全响应一阶电路的全响应 用电路图可描述如下： 1.1. 74 一阶电路的全响应一阶电路的全响应 例例741 图示电路，当 0t 时电路已处于 稳态， 0t 时 打开， 合上， 1 K 2 K 求 时 0t ( ) L i t 和 ， 并画出波形图。 ( )u t 1.1. 74 一阶电路的全响应一阶电路的全响应 解：解： 0t 1 K 2 K 时， 闭合 打开，电路已处于稳态 105 (0 )A 63 L i 时 打开 闭合 0t 1 K

26、 2 K 5 (0 )(0 )A 3 1 =S 4 LL ii L R 电路的响应是全响应 全响应=零输入响应+零状态响应 1.1. 74 一阶电路的全响应一阶电路的全响应 先求零输入响应 4 5 ( )(0 )A 3 t t LziL itiee 再求零状态响应 ( )2A L i 4 ( )( )(1)2(1)A t t LzsL itiee 444 51 ( )2(1)2A 33 ttt LLziLzs i tiieee 4 ( )44 ( )V 3 t L di t u tLe dt 1.1. 75 求解一阶电路的三要素公式求解一阶电路的三要素公式 恒定激励下求解一阶电路的三要素公式为

27、 ( )( ) (0 )( ) t y tyyye (751) 式中 ( )y t 0t 是一阶电路 后的任意时刻的任意响应； (0 )y 是 的初始值，求法见72节； ( )y t ( )y 是 的终值，将电路中电容开路，电 感短路算出的响应值； ( )y t 1.1. 75 求解一阶电路的三要素公式求解一阶电路的三要素公式 是时间常数， RC电路中 i RC，RL电路 , ii i L G LR R 是从储能元件两端看进去的戴维 南等效电阻。 (0 )y ( )y 、 、 是公式中的三要素。 1.1. 75 求解一阶电路的三要素公式求解一阶电路的三要素公式 例例 751 电路如图751所示

28、， 0t 时开关闭 合，开关闭合之前电路已处于稳态，求 0t 时 ( ), ( ) L i t i t 。 1.1. 75 求解一阶电路的三要素公式求解一阶电路的三要素公式 解：解：电路的激励是直流，属于恒定激励，可以 用三要素公式求解 （1）求初始值 0t 时 (0 )0A L i 由换路定则可得 (0 )(0 )0A LL ii 由 时电路可求出 0t 12 (0 )2A 42 L i 1.1. 75 求解一阶电路的三要素公式求解一阶电路的三要素公式 （2）求终值 t 时L等效为短路 12 ( )6A 2 L i ( )0Ai （3）求时间常数 由电感L两端看进去的戴维南等效电阻 2 44

29、 243 R 3 S 4 L R 1.1. 75 求解一阶电路的三要素公式求解一阶电路的三要素公式 （4）代入三要素公式求得 ( )( ) (0 )( ) t LLLL i tiiie 4 3 66A 0 t et ( )( ) (0 )( ) t i tiiie 4 3 2A 0 t et 和 的变化曲线如图所示 ( ) L i t( )i t 1.1. 75 求解一阶电路的三要素公式求解一阶电路的三要素公式 例例752 图（a）所示电路， 0t 时电路处 于稳态， 0t 时开关闭合，求 0t 时的 ( ) c u t和 ( ) c i t 。 解：解：（1）求初值 0t 时， (0 ) 5

30、V c u 据换路定则可求得 (0 )(0 )5V cc uu 时开关合上，由 0t 1 (0 )A 4 C i 图b求出 1.1. 75 求解一阶电路的三要素公式求解一阶电路的三要素公式 （2）求终值 t 时，C可视为开路 ( )105 c ui 又 520105iii 1 A 5 i 代入上式 ( )253V c u ( )0A c i 1.1. 75 求解一阶电路的三要素公式求解一阶电路的三要素公式 （3）求 值 由电路求出 0 1020()5iiii 0 5 4 ii 0 10ui 0 0 10 8 5 4 i ui R i i 8 216S i RC 1.1. 75 求解一阶电路的三

31、要素公式求解一阶电路的三要素公式 （4）代入三要素公式得出 ( )( )(0 )( ) t cccc u tuuue 16 32V 0 t et ( )( ) (0 )( t cccc i tiiie 16 1 A 0 4 t et 16 ( )1 ( )A 0 4 t c c du t i tCet dt 或者 1.1. 75 求解一阶电路的三要素公式求解一阶电路的三要素公式 和 变化曲线如图所示 ( ) c u t( ) c i t 1.1. 76 RC， RL微分电路与积分电路微分电路与积分电路 微分和积分电路是脉冲电路中经常 使用的电路，顾名思义，电路因能实 现微分运算和积分运算而得名

32、，RC， RL微分积分电路是一阶电路的瞬态分 析的实际应用电路。 1.1. 761 RC，RL微分电路微分电路 一一 、RC微分电路微分电路 分析图示电路，列写KVL方程 12 ( )( )( ) c u tu tu t 2 11 ( )( )( ) tt c u ti t dtu t dt CRC 1.1. RC微分电路微分电路 若RC取值非常非常小 22 1 ( )( ) t u t dtu t RC 与之相比可忽略 则 2( ) u t 21 1 ( )( ) t u t dtu t RC 1 2 ( ) ( ) du t u tRC dt 于是有 上式表明，输出电压近似输入电压的微分，

33、 故称该电路为微分电路。 1.1. RC微分电路微分电路 1.1. R微分电路微分电路 输出 为矩形脉冲，讨论各响应电压的情况 如下： 1( ) u t 当 时 0t (0 )0 c u 0t 当 时 (0 )(0 )0 cc uu 12 ( ), ( )u tEu tE ( ) C ut E 0 t （b） E 0 t （c） E E 0 T t 1( ) u t （a） 图 772 2( ) u t 1.1. R微分电路微分电路 当 时 0tT ( )(1) t RC C utEe 2( ) t RC u tEe 由于 取值非常非常小， RC T 电容充电速度很快。 当 时 T 1( )u

34、 TE ()(1) T RC C uTEeE 2( )0 T RC u TEe ( ) C ut E 0 t （b） E 0 t （c） E E 0 T t 1( ) u t （a） 图 772 2( ) u t 1.1. R微分电路微分电路 1( )0u T () C uTE 2( )u TE 当 时 tT 1( ) 0u t ( ) t T RC C utEe 2( ) t T RC u tEe 从输入、输出 电压波形可以看出：微分电路起到了波形 变换作用，将输入的矩形脉冲变换成输出 的一对尖脉冲。 1.1. RL微分电路微分电路 RL微分电路电路，请读者自行完成分 析过程。 1.1. 7

35、62 RC、RL积分电路积分电路 图所示的电路在时间常数 远大于输入脉 冲宽度T时，为积分电路。 本节以RC积分电路为例进行分析。 列写图(a)电路的KVL方程 1.1. RC积分电路积分电路 12 ( )( )( ) R u tutu t 2 12 ( ) ( ) du t uRCu t dt 当RC取值非常非常大， 上式近似为 2 1 ( )du t uRC dt 两边对t积分并整理为 21 1 ( )uu t dt RC 输出电压 近似输入电压 的积分，故称为积 分电路。 2 u 1 u 1.1. 当输入矩形脉冲时，讨论各响应的情况如下： 当 时， 当 时， 当 时， 0t 12 ( )

36、0, (0 )0, ( )0 R u tuut 0t 122 ( ), (0 )(0 )0, (0 ) R u tEuuuE 0tT 1( ) u t 给电容C充电， 2( ) (1) t RC u tEe 12 ( )( )( ) R utu tu t t RC e 由于 ，所以指数函数变化速度很慢，其 波形如图所示。 T RC积分电路积分电路 1.1. RC积分电路积分电路 当 时， tT 22 ()()(1) T RC u Tu TEe 1( )0u T 2 ()()(1) T RC R u Tu TEe 当 时，电容放电， 指数下降 tT 2( ) u t 2( ) (1) Tt T

37、RCRC u tEee ( )(1) Tt T RCRC R utEee 1.1. RC积分电路积分电路 从输入、输出电压 波形可以看出：积分 电路起到了波形变换 作用，将输入的矩形 脉冲变换成输出的近 似三角脉冲。 1.1. 77 二阶电路的零输入响应二阶电路的零输入响应 RLC串联电路，设开关闭合前电容有初始储能 00 (0 ), (0 ) cc uU iI （设 ）。 0 0I 0t 时开关闭合，此时以后电容将通过电阻 和电感放电直至放电结束。以下分析电容的放电 规律。 1.1. 77 二阶电路的零输入响应二阶电路的零输入响应 0t 时根据KVL可得 ( )( )( )0 CLR utu

38、 tu t 因 ( )( ) RL u tRi t ( ) ( ) L L di t utL dt 1 ( )( ) t cL u ti t dt C 代入上式并整理可得 2 2 ( )( )1 ( )0 cc c d i tdi tR i t dtLdtLC 1.1. 77 二阶电路的零输入响应二阶电路的零输入响应 其特征方程为 2 1 0 R SS LLC 设特征根为 12 ,s s 12 ()()0ssss 2 1,2 1 () 22 RR s LLLC 12 ,s s 称为二阶电路的自然频率（固有频率）， 由于有两个自然频率，所以二阶电路的零输入 响应包含两项指数函数分量 1.1. 7

39、7 二阶电路的零输入响应二阶电路的零输入响应 12 12 ( ) s ts t L i tAeA e （771） (0 )(0 )0 (0 )11 (0 )(0 )(0 ) LL L LLc ii di uRiu dtLL 0 1U L 由初始条件 来确定 1 2 ,A A 12 0 1122 (0 )0 (0 ) L L iAA Udi s As A dtL （772） 则 1.1. 77 二阶电路的零输入响应二阶电路的零输入响应 联立上式并求得 0 12 21 () U AA L ss 由于R,L,C数值不同，特征根 和 1 S 现四种不同情况： 2 S可能出 (a) 当 时， 0R 1,

40、2 1 Sj LC 是一对共轭虚数； (b) 当 时，即 2 1 () 2 R LLC 2 L R C 时， ， 一对实部为负的共轭复数； 1 S 2 S为 1.1. 77 二阶电路的零输入响应二阶电路的零输入响应 (c) 当 时，即 2 1 () 2 R LLC 2 L R C 时， 1 S ， 2 S为 不相等的负实数； (d) 当 时，即 2 1 () 2 R LLC 2 L R C 时， 1 S， 2S 为相等的负实数。 若 ， 的量纲与电阻相同，称 2 1 () 2 R LLC n R n R 阻尼电阻，则电路中的电阻 为 0R称为无阻尼 ，称为欠阻尼， n RR n RR 称为临界

41、阻尼， n RR 称为过阻尼。 1.1. 77 二阶电路的零输入响应二阶电路的零输入响应 (a)、(b)、(c) 三种情况电路的响应为 12 0 21 ( )() () s ts t L U i tee L SS 12 0 21 21 ( )( )( )() s ts t cLL U u tRi tutS eS e SS （773） 对于上述四种情况分别讨论如下： 1、 0R ，无阻尼状态 1,2 1 Sj LC 代入773式 1.1. 77 二阶电路的零输入响应二阶电路的零输入响应 电感电流和电容电压分别为 00 ( )sin 2 tt jj LCLC L C eeCt i tUU LjLL

42、C 00 sin C U L （774） 其中 量纲为 0 1 LC rad/s ，称为角频率 ( ) ( )( ) L cL di t u tutL dt 000 coscos t UUt LC （775） 1.1. 77 二阶电路的零输入响应二阶电路的零输入响应 和 波形，电路的响应是按等幅正弦方式 变化的，电路为 ( ) L i t( ) c u t 1.1. 77 二阶电路的零输入响应二阶电路的零输入响应 从物理意义来看，电容C中贮存的电场能量通 过给电感L充电转化为磁场能量存于电感中， ( ) c u t 下降 ( ) L i t增大， ( ) c u t 下降到零时，电感储能 (

43、) L i t ( ) L i t ( ) c u t 幅度达到最大。随后电感有反向给电容充电 下降 增大， ( ) L i t下降到零时，电容储能 ( ) c u t 幅度达到最大。这样电路的储能在电场和磁场 之间往复不已，由于电路中无损耗，振荡将无 衰减的进行下去。所以也称为无阻尼自由振荡 或谐振。 1.1. 77 二阶电路的零输入响应二阶电路的零输入响应 2、 2 L R C 2 1 () 2 R LLC 欠阻尼状态 由于 将特征根 2 1,2 1 () 22 RR S LLLC 是一对共轭复数。 令 2 22 0 1 , () 22 RR LLLC 则 1,2 Sj 1.1. 77 二阶电路的零输入响应二阶电路的零输入响应 代入式（773）可得 0 ( )() 2 tj ttj t L U i teeee j L