备战2021高考 专题02 函数（教师版含解析）

《备战2021高考 专题02 函数（教师版含解析）》由会员分享，可在线阅读，更多相关《备战2021高考 专题02 函数（教师版含解析）（18页珍藏版）》请在七七文库上搜索。

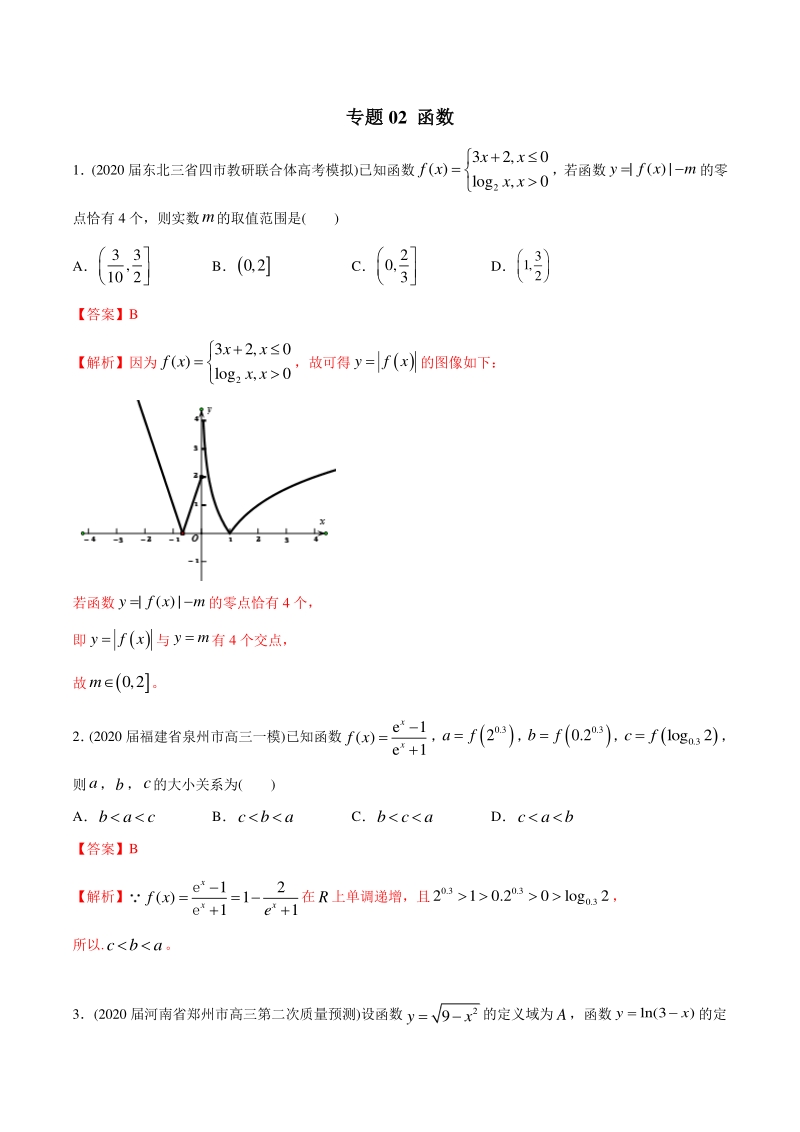
1、专题专题 02 函数函数 1(2020 届东北三省四市教研联合体高考模拟)已知函数 2 32,0 ( ) log,0 xx f x x x ，若函数|( )|yf xm的零 点恰有 4 个，则实数m的取值范围是( ) A 33 , 10 2 B0,2 C 2 0, 3 D 3 1, 2 【答案】B 【解析】因为 2 32,0 ( ) log,0 xx f x x x ，故可得 yf x的图像如下： 若函数|( )|yf xm的零点恰有 4 个， 即 yf x与y m 有 4 个交点， 故0,2m。 2 (2020 届福建省泉州市高三一模)已知函数 e1 ( ) e1 x x f x ， 0.3

2、 2af， 0.3 0.2bf， 0.3 log2cf， 则a，b，c的大小关系为( ) Abac Bcba Cbca Dcab 【答案】B 【解析】 12 ( )1 11 e e x xx f x e 在R上单调递增，且 0.30.3 0.3 210.20log2 ， 所以.cba。 3(2020 届河南省郑州市高三第二次质量预测)设函数 2 9yx 的定义域为A，函数 ln(3)yx 的定 义域为B，则AB ( ) A( ,3) B( 8, 3) C3 D 3,3) 【答案】D 【解析】由题意，对于函数 2 9yx ， 2 90 x ，解得33x ，即3,3A ； 对于函数 ln(3)yx

3、 ，30 x，解得3x，即,3B ，所以AB 3,3)。 4(2020 届河南省郑州市高三第二次质量预测)函数 2 | | ( ) 24 x x f x 的图象大致为( ) A B C D 【答案】D 【解析】由题意，函数 2 | | ( ) 24 x x f x 的定义域为,2x xx R， 又 2 2 | | () 2424 xx xx fx ，即()( )fxf x，所以 ( )f x是偶函数，可排除 A、B 选项； 当0,2x时， 2 ( )0 24 x x f x ；当2,x时， 2 ( )0 24 x x f x ，只有 D 符合题意。 5(2020 届河南省郑州市高三第二次质量预

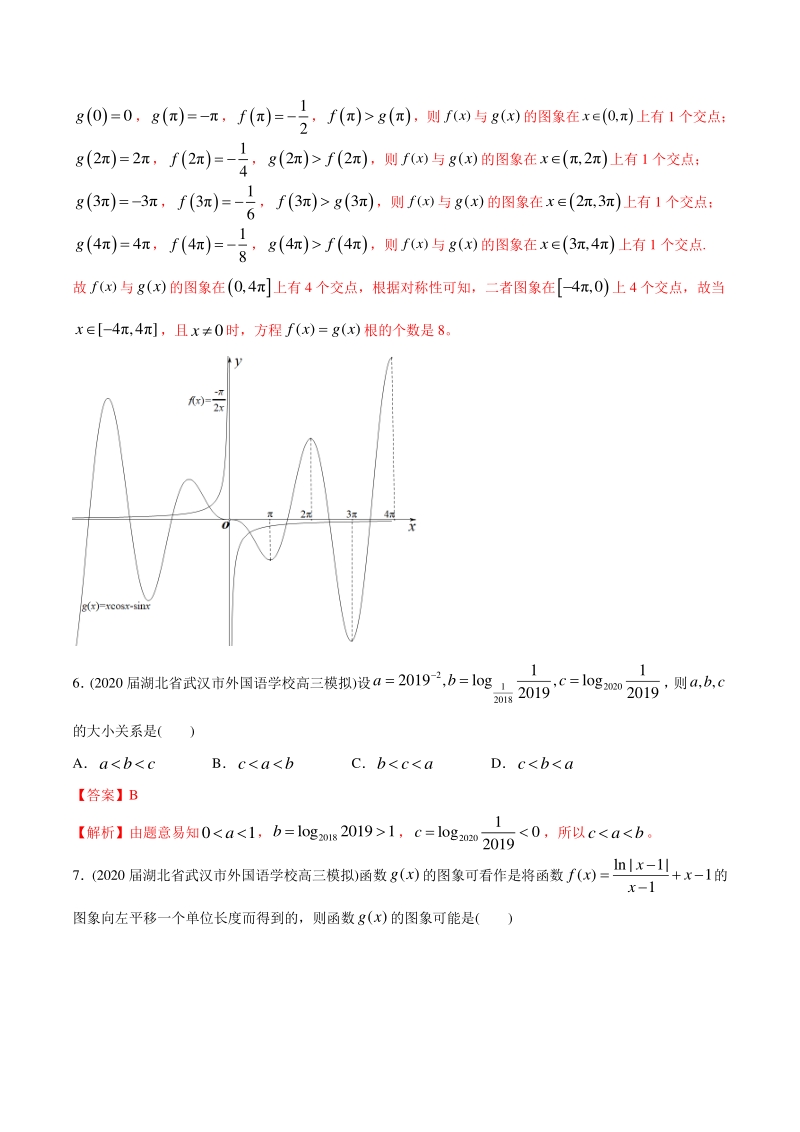
4、测)已知函数 ( ) 2 f x x ，( )cossing xxxx，当 4,4x ，且 0 x时，方程 ( )( )f xg x 根的个数是( ) A5 B6 C7 D8 【答案】D 【解析】由题意，函数 ( ) 2 f x x ，在 4,00,4上是奇函数，且是反比例函数， 又 ()cossincossingxxxxxxxg x， 所以( )g x在 4,00,4上是奇函数. 又( )sing xxx ， 所以 0,x 时，( )0g x ；,2x时，( )0g x ；2,3x时，( )0g x ； 3,4x时，( )0g x ， 所以( )g x在0,上单调递减； 在,2上单调递增；

5、在2,3单调递减； 在3,4上单调递增。作出( ), ( )f x g x的图象，如下图所示， 00g， g ， 1 2 f ， fg，则( )f x与( )g x的图象在0,x上有 1 个交点； 22g， 1 2 4 f ，22gf，则( )f x与( )g x的图象在,2x上有 1 个交点； 33g ， 1 3 6 f ，33fg，则( )f x与( )g x的图象在2,3x上有 1 个交点； 44g， 1 4 8 f ，44gf，则( )f x与( )g x的图象在3,4x上有 1 个交点. 故 ( )f x与( )g x的图象在 0,4上有 4 个交点，根据对称性可知，二者图象在4,0

6、上 4 个交点，故当 4,4x ，且 0 x时，方程 ( )( )f xg x 根的个数是 8。 6 (2020 届湖北省武汉市外国语学校高三模拟)设 2 12020 2018 11 2019 ,log,log 20192019 abc ， 则, ,a b c 的大小关系是( ) Aabc Bcab Cbca Dcba 【答案】B 【解析】由题意易知01a， 2018 log20191b ， 2020 1 log0 2019 c ，所以cab。 7(2020 届湖北省武汉市外国语学校高三模拟)函数( )g x的图象可看作是将函数 ln|1| ( )1 1 x f xx x 的 图象向左平移一个

7、单位长度而得到的，则函数( )g x的图象可能是( ) A B C D 【答案】C 【解析】由已知可得 ln | ( )(1) x g xf xx x ， 显然()( )gxg x ，故( )g x为奇函数， 其图象关于原点对称，排除 A； 当x趋向于正无穷大时，( )g x趋向于正无穷大，排除 D； (1)10g ，排除 B，故选 C。 8(2020 届湖北省宜昌市高三调研)设 1 3 1 2 x ， 5 1 log 6 y ， 1 4 log 3z ，则( ) Ax yz By zx Cz xy Dz yx 【答案】B 【解析】 1 3 1 0( ) 2 1， 55 1 loglog 61

8、 6 ， 14 4 log 3log 3( 1,0) ，x zy 故选 B。 9(2020 届湖北省宜昌市高三调研)对于函数 2 1 x fx e 的图象，下列说法正确的是 ( ) A关于直线1x 对称 B关于直线y x 对称 C关于点1,0对称 D关于点0,1对称 【答案】D 【解析】 21 1 11 11 x xx e f x ee ， 令 1 1 x x e g xxR e ，则 11 11 xx xx ee gxg x ee ， g x为奇函数，其图象关于原点对称， 将 g x图象向上平移 1 个单位长度可得 f x图象， 所以 f x图象关于0,1对称，故选 D。 10(2020 届

9、湖北省宜昌市高三调研)若函数 2 ( )1 x f xexax在区间1,2内有且仅有一个零点，则实 数a的取值范围是 A 2 5 ,) 2 e B( ,2e C 2 5 (,2) 2 e e D 2 5 ,2 2 e e 【答案】D 【解析】令( )0f x ，即 2 10 x exax ，分离参数可得 1 x e ax xx ，令 1 ( ) x e g xx xx ，则 2 (1)(1) ( ) x xex g x x ，令( )1 x h xxe ，则( )1 x h xe ，当0 x时 ( )0h x ，所以当0 x时 ( )(0)0h xh ，所以当12x时)(0g x ，所以函数(

10、 )g x在(1,2)上单调递减，所以当 1,2x 时， (2)( )(1)gg xg ，即 2 5 ( )2 2 e g xe ，又函数 ( )f x在区间1,2内有且仅有一个零点，所以 2 5 2 2 e ae ，故实数a的取值范围是 2 5 ,2 2 e e ，故选 D。 11(2020 届湖南省永州市高三第三次模拟)已知函数 5 sin 12 fxx ，要得到函数 cosg xx的图 象，只需将 yf x的图象( ) A向左平移 12 个单位长度 B向右平移 12 个单位长度 C向左平移 5 12 个单位长度 D向右平移 5 12 个单位长度 【答案】A 【解析】因为sincos 12

11、2 fxxx ， 故要得到 g x，只需将 f x向左平移 12 个单位长度，故选 A。 12(2020 届湖南省永州市高三第三次模拟)已知 0.2 1 2 a ， 1 2 0.2b ， 1 3 log 2c ，则( ) Aab c Bbac Cbca Dacb 【答案】B 【解析】由于 0.20 11 01 22 ， 1 2 1 0.25 1 5 ， 11 33 log 2log 10 故bac，故选 B。 13(2020 届湖南省永州市高三第三次模拟)已知函数 f x是定义在 R 上的奇函数，且满足 11fxfx，当0,1x时， ax f xe (其中 e 是自然对数的底数)，若2020

12、ln28f， 则实数 a 的值为( ) A3 B3 C 1 3 D 1 3 【答案】B 【解析】由已知可知， 2fxfxf x ，所以函数 f x是一个以 4 为周期的周期函数， 所以 ln2 2020 ln2ln2ln228 aa fffe， 解得3a ，故选 B。 14(2020 届全国名校高三模拟)函数 1 1 x x e f x xe (其中e为自然对数的底数)的图象大致为( ) A B C D 【答案】A 【解析】 f(x) 111 111 xxx xxx eee xex exe f(x)， f(x)是偶函数，故 f(x)图形关于 y 轴对称，排除 C，D； 又 x=1 时， e1

13、1 1 e f 0， 排除 B，故选 A。 15(2020 届全国名校高三模拟)已知1 ba，则下列大小关系不正确的是( ) A ba aa B ab bb C bb ab D ba ab 【答案】D 【解析】1 ba， x ya和 x yb均为增函数， ba aa， ab bb，A，B 项正确， 又 b yx在(0, )为增函数， bb ab， C 项正确； b a和 a b的大小关系不能确定，如3,2, ba abab； 4,2, ba abab；5,2, ba abab ，故 D 项不正确，故选 D。 16(2020 届全国名校高三模拟)已知函数( )(ln) x e f xkxx x

14、，若1x 是函数 ( )f x的唯一极值点，则 实数k的取值范围是( ) A( , e B(, ) e C(,)e D,)e-+ ? 【答案】A 【解析】由函数 ln x e f xkxx x ，可得 2 11 1 xxx e xexe fxk xxxx ， f x有唯 一极值点 1,0 xfx 有唯一根1x ，0 x e k x 无根，即y k 与 x e g x x 无交点，可得 2 1 x ex gx x ，由 0gx 得， g x在1上递增，由 0gx 得， g x在0,1上递减， min 1,g xgeke ，即实数k的取值范围是,e，故选 A. 17 (2020 届三湘名校教育联盟

15、高三第二次大联考)已知函数 3 2 ,0 log,0 x x f x x x ， 则 3 = 3 ff ( ) A 2 2 B 1 2 C 3 log 2 D 3 log 2 【答案】A 【解析】依题意 1 2 33 331 loglog 3 332 f ， 1 2 312 2 322 fff ，故选 A。 18(2020 届三湘名校教育联盟高三第二次大联考)已知函数 cos|sin |f xxx，有下列四个结论： f x是偶函数 f x是周期函数 f x在,0上是增函数 f x在, 上恰有两个零点 其中所有正确结论的编号有( ) A B C D 【答案】C 【解析】由于 cossincoss

16、infxxxxxf x，所以 f x为偶函数，故正确； 由于 2cos2sin2cossinf xxxxxf x，所以 f x是周期为2的周期函 数，故正确；当,0 x 时，sin0 x，所以 cossin2sin 4 f xxxx ，且 3 , 444 x ，所以 f x在,0上先减后增，错误；当,x 时，令 0f x ，得 cossinxx，所以tan1x ，且, 2 2 x ，所以 f x有两个零点 12 , 44 xx ，所以正确. 综上所述，正确结论的编号有，故选 C。 19(2020 届三湘名校教育联盟高三第二次大联考)定义在R上的奇函数 f x满足 330fxf x ，若 11f

17、， 22f ，则 1232020ffff( ) A1 B0 C1 D2 【答案】C 【解析】由已知 f x为奇函数，得 fxf x， 而330fxf x ， 所以33f xf x， 所以 6f xf x，即 f x的周期为6. 由于 11f， 22f ， 00f， 所以 33330ffff， 4222fff， 5111fff， 600ff. 所以 1234560ffffff， 又20206 3364 ， 所以 1232020ffff 12341ffff，故选 C。 20(2020 届陕西省咸阳市高三第一次模拟)函数cos 4 yx 的单调递增区间是( ) A 13 2,2 44 kk ()k

18、Z B 37 2,2 44 kk ()k Z C 31 2,2 44 kk ()k Z D 15 2,2 44 kk ()k Z 【答案】C 【解析】令22 4 kxkkZ ，解得 31 22 44 kxkkZ， 因此，函数cos 4 yx 的单调递增区间是 31 2,2 44 kkkZ ，故选 C。 21(2020 届四川省宜宾市高三第二次诊断)函数 cos 2 fxxx 的图象大致为( ) A B C D 【答案】A 【解析】根据题意， cossin 2 fxxxxx ，定义域为R，定义域关于原点对称. 有 sinsinfxxxxxf x ，即函数 yf x为偶函数，排除 B、D； 当0,

19、x时，0 x，sin0 x，有 0f x ，排除 C，故选 A。 22(2020 届四川省宜宾市高三第二次诊断)若定义在R上的偶函数 f x满足 20f xfx当 0,1x， 2 1f xx ，则( ) A 12 3 5 log 2log 3 2 fff B 12 3 5 log 2log 3 2 fff C 12 3 5 log 2log 3 2 fff D 21 3 5 log 3log 2 2 fff 【答案】A 【解析】因为定义在R上的偶函数 yf x满足 20f xfx，即 20f xf x， 即 2f xf x， 24f xf xf x， 所以，函数 yf x的周期为4， 因为当0

20、,1x时， 2 1f xx 单调递减， 因为 511 0 222 fff ， 22 4 log 3log0 3 ff ， 133 3 log 2log 2log 20fff ， 因为 2 41 0log1 32 ，所以 2 41 log 32 ff ， 所以， 12 3 14 log 2log 23 fff ，即 12 3 5 log 2log 3 2 fff ，故选 A。 23(2020 届云南省曲靖市第二中学高三第一次模拟)函数 24sinf xxx， , 2 2 x 的图象大致是 ( ) A B C D 【答案】D 【解析】 函数 f(x)=2x4sinx，f(x)=2x4sin(x)=

21、(2x4sinx)=f(x)，故函数 f(x)为奇函数， 所以函数 f(x)=2x4sinx 的图象关于原点对称，排除 AB， 函数 f(x)=24cosx，由 f(x)=0 得 cosx= ，故 x=2k(kZ)， 所以 x=时函数取极值，排除 C，故选 D。 24(2020 届云南省曲靖市第二中学高三第一次模拟)定义在R上的可导函数 f x满足 11f，且 2 1fx ，当 3 , 22 x 时，不等式 2 3 (2cos )2sin 22 x fx 的解集为( ) A 4 , 33 B 4 , 33 C0, 3 D, 3 3 【答案】D 【解析】令 11 ( )( ) 22 g xf x

22、x，则 1 ( )( )0 2 g xfx， ( )g x 在定义域R上是增函数，且 11 (1)(1)0 22 gf， 1 (2cos )(2cos )cos 2 gxfxx 2 3 = (2cos )2sin 22 x fx ， 2 3 (2cos )2sin0 22 x fx 可转化成 (2cos )1gxg，得到 2cos1x，又 3 , 22 x ，可以得到, 3 3 x 25(2020 届安徽省蚌埠市高三第三次质检)已知函数 f x是一次函数，且 23ffxx 恒成立，则 3f( ) A1 B3 C5 D7 【答案】D 【解析】设 f xaxb，0a， 则 2 2222bff xx

23、f axbxaxbabaa xabx 因为 23ff xx 恒成立，所以 2 20aa且3abb，解得 2,1ab ， 所以 21f xx，即有 37f. 26(2020 届安徽省蚌埠市高三第三次质检)已知函数 2 1 2,1 2 1 log,1 2 x x f x xx ，若函数 0g xxm m 与 yf x的图象相交于 A，B 两点，且 A，B 两点的横坐标分别记为 1 x， 2 x， 则 12 xx的取值范围是( ) A 3 1, 2 B 2 5 log 3, 2 C 5 1, 2 D 2 log 3,3 【答案】B 【解析】作出函数 ( )f x，( )g x的图象如图，不妨设 12

24、 xx ， 当( )yg x经过点 3 (1, ) 2 时， 5 2 m ， 联立 2 5 2 1 log () 2 yx yx 得 3 2 x ，所以 2 3 1, ) 2 x ； 因为 2 1 log () 2 yx与 1 2 2 x y 的图象关于直线y x 对称，而y xm 与y x 垂直，所以 12222 1 log () 2 xxxx，且 2 3 1, ) 2 x . 令 2 1 ( )log () 2 h xxx，且 3 1, ) 2 x， 则易知( )h x为增函数，所以 3 (1)( )( ) 2 hh xh， 因为 2 35 (1)log 3, ( ) 22 hh，所以 2

25、12 5 log 3, ) 2 xx. 故选 B. 27(2020 届百校联考高考考前冲刺)下列函数中既关于直线1x 对称，又在区间 1,0 上为增函数的是 ( ) A sinyx. B|1|yx C cosyx Dee xx y 【答案】C 【解析】当1x 时，sin01yx ，所以sinyx不关于直线1x 对称，则 A 错误； 1,1 1 1,1 xx yx xx ，所以在区间 1,0上为减函数，则 B 错误； xx yf xee，而 22 02,2ffee， 则 02ff， 所以ee xx y 不关于直线1x 对称， 则 D 错误； 故选 C。 28(2020 届百校联考高考考前冲刺)已

26、知函数( )(0 x f xmm m，且 1)m 的图象经过第一、二、四象 限，则|( 2)|af， 3 8 4bf ，|(0)|cf的大小关系为( ) Acba Bcab Cabc Dbac 【答案】C 【解析】因为( )(0 x f xmm m，且 1)m 的图象经过第一、二、四象限， 所以01m，(1)0f， 所以函数 ( )f x为减函数，函数|( )|f x 在(,1)上单调递减，在(1,)上单调递增， 又因为 313 824 122422 ， 所以ab， 又|(0)| 1cfm ， 2 |(2)|fmm， 则| 2 |(2)|(0)|10ffm ， 即|(2)| |(0)|ff，

27、所以abc，故选 C。 29(2020 届博雅闻道高三联合质量评测)已知 5 6 2a ， 1 2 3 log 5 b ， 1 ln 2 c ，则a、b、c的大小关系是 ( ) Aabc Bcab Ccba Dbca 【答案】C 【解析】指数函数2xy 为R上的增函数，则 5 0 6 221a ； 对数函数 1 2 logyx 为0,上的减函数，则 111 222 31 log 1loglog 52 ，即01b； 对数函数lnyx为0,上的增函数，则 1 lnln10 2 c . 因此，cba，故选 C。 30(2020 届博雅闻道高三联合质量评测)函数 | | ( )sin| 2 x f x

28、ex的部分图象大致为( ) A B C D 【答案】D 【解析】由 | | ( )sin| 2 x f xex可知 ()( )fxf x ，其定义域为R关于原点对称,所以函数 ( )f x为偶函 数， 其图象关于y轴对称， 故排除选项 C； 又当(0,)x，( )sin2 x f xex， ( )cos0 x fxex ， 所以函数 f x的图象在(0,)上单调递增，故排除选项 B；又因为 1 (1)sin12sin221 62 feee ，故排除选项 A。 31(2020 届博雅闻道高三联合质量评测)已知函数( )sin 2 6 f xx ，则下列结论正确的个数有( ) 3 x 是函数( )

29、f x图像的一条对称轴 7 ,0 12 是函数 ( )f x图像的一个对称中心 将函数 ( )f x图像向右平移 6 单位所得图像的解析式为得( )cos2f xx 函数( )2sin 2 6 f xx 在区间, 6 3 内单调递增 A1 B2 C3 D4 【答案】D 【解析】对于选项：因为当 3 x 时，由( )sin 2 6 f xx 得，sin 21 336 f ，所以 3 x 是函数( )f x图象的一条对称轴，即选项正确； 对于选项：令( )02 6 f xxk ，kz，即 122 k x ，kz，当 7 1 12 kx ，所以 7 ,0 12 是函数 ( )f x图象的一个对称中心

30、，即选项正确； 对于选项：将函数( )sin 2 6 f xx 图象右移 6 得到图象解析式为 sin 2cos2 66 yxx ，即选项正确； 对于选项：令222 262 kxk 剟，kz， 即得 63 kxk 剟，kz，当0k 时， 63 x 剟， 所以函数 ( )f x在区间, 6 3 内单调递增，即选项正确； 综上所述正确选项有 4 个。 32(2020 届四川省遂宁市高三二诊)已知 ( )f x是定义在R上的偶函数，其导函数为 ( )fx 若0 x时， ( )2fxx ，则不等式 2 (2 )(1)321fxf xxx的解集是_ 【答案】 1 1, 3 【解析】令 2 ( )( )g

31、 xf xx，则( )g x是R上的偶函数， ( )( )20g xfxx ，则( )g x在(0,)上递减，于是在(,0)上递增 由 2 (2 )(1)321fxf xxx得 22 (2 )(2 )(1)(1)fxxf xx， 即(2 )(1)gxg x， 于是(|2 |)(|1|)gxgx， 则|2 | |1|xx， 解得 1 1 3 x 。 33(2020 届博雅闻道高三联合质量评测)已知函数 2 ( )lnf xx x ，则函数( )f x的极小值为_. 【答案】ln21 【解析】 2 ( )lnf xx x 0 x ， 2 2 ( ) x fx x ，当( ) 0fx =时2x， 所

32、以函数 ( )f x在(0,2)上单调递减，在(2,)上单调递增， 所以函数 ( )f x极小值为(2)ln21f. 34(2020 届福建省泉州市高三一模)若函数 2,0 ( ) 2 ,0 x f x x x ，则使得不等式( ( )0f f a成立的a的取值 范围为_. 【答案】0, 【解析】 2,0 ( ) 2 ,0 x f x x x ， 当0a时， 220ff af，0a 符合； 当0a 时， 2 0ff afa a ，0a 不满足( ( )0f f a. 故答案为：0, 35(2020 届河南省郑州市高三第二次质量预测)幂函数 2 ( )33 m f xmmx 的图象关于y轴对称，

33、则 实数m_. 【答案】2 【解析】函数 2 ( )33 m f xmmx 是幂函数， 2 331,mm 解得：1m或2m， 当1m时，函数y x 的图象不关于y轴对称，舍去， 当2m时，函数 2 yx=的图象关于y轴对称， 实数2m 36(2020 届四川省宜宾市高三第二次诊断)已知 sinf xxxm 为奇函数，则 2 f _ 【答案】1 2 【解析】由奇函数的性质可得 00fm，故 sinf xxx，所以1 22 f 37(2020 届湖北省武汉市外国语学校高三模拟)已知函数( )fx 是奇函数( )()f x xR的导函数，且满足 0 x时， 1 ln( )( )x fxf x x 则

34、不等式(2020) ( )0 xf x的解集为_. 【答案】0,2020 【解析】设( )ln( )g xx f x，则 1 ( )( )ln( )g xf xx fx x . 因为当0 x时， 1 ln( )( )x fxf x x ，所以当0 x时，函数( )g x单调递减. 因为(1)0g，所以当01x时，( )0g x，当1x 时，( )0g x. 因为当01x时，ln0 x，当1x 时，ln0 x， 所以当0 x且1x 时，( )0f x ，又 1 (1) ln1(1) 1 ff ，所以(1)0f， 所以当0 x时，( )0f x . 又 ( )f x为奇函数，所以当 0 x时， ( )0f x ， 所以不等式(2020) ( )0 xf x可化为 0 20200 x x 或 0 20200 x x 解得02020 x，所以不等式的解集为(0,2020)。