专题20 矩形存在性问题巩固练习（基础）-2021年中考数学几何专项复习（教师版含解析）

《专题20 矩形存在性问题巩固练习（基础）-2021年中考数学几何专项复习（教师版含解析）》由会员分享，可在线阅读，更多相关《专题20 矩形存在性问题巩固练习（基础）-2021年中考数学几何专项复习（教师版含解析）（15页珍藏版）》请在七七文库上搜索。

1、矩形存在性问题巩固练习矩形存在性问题巩固练习(基础基础) 1 如图， 点 O 是平行四边形 ABCD 的对称中心， 将直线 DB 绕点 O 顺时针方向旋转， 交 DC、 AB 于点 E、 F (1)证明：DEOBFO； (2)若 DB2，AD1，AB 当 DB 绕点 O 顺时针方向旋转 45时，判断四边形 AECF 的形状，并说明理由； 在直线 DB 绕点 O 顺时针方向旋转的过程中，是否存在矩形 DEBF，若存在，请求出相应的旋转角度(结 果精确到 1)；若不存在，请说明理由 【解答】(1)见解析；(2)菱形；127 【解析】(1)证明：在平行四边形 ABCD 中，CDAB， CDOABO，

2、DEOBFO 又点 O 是平行四边形的对称中心，ODOB，DEOBFO； (2)四边形 AECF 是菱形理由如下： 在ABD 中，DB2，AD1，AB，DB2AD2AB2 ABD 是直角三角形，且ADB90 ODOBDB1，ADOD1 OAD 是等腰直角三角形，AOD45 当直线 DB 绕点 O 顺时针旋转 45时，即DOE45，AOE90 DEOBFO，OEOF 又点 O 是平行四边形的对称中心，OAOC 四边形 AECF 是平行四边形四边形 AECF 是菱形 当四边形 DEBF 是矩形时， 则有DFBFDE90，ODOE 又ADB90 有ADFODEDEO 在 RtADF 中，ADF26.

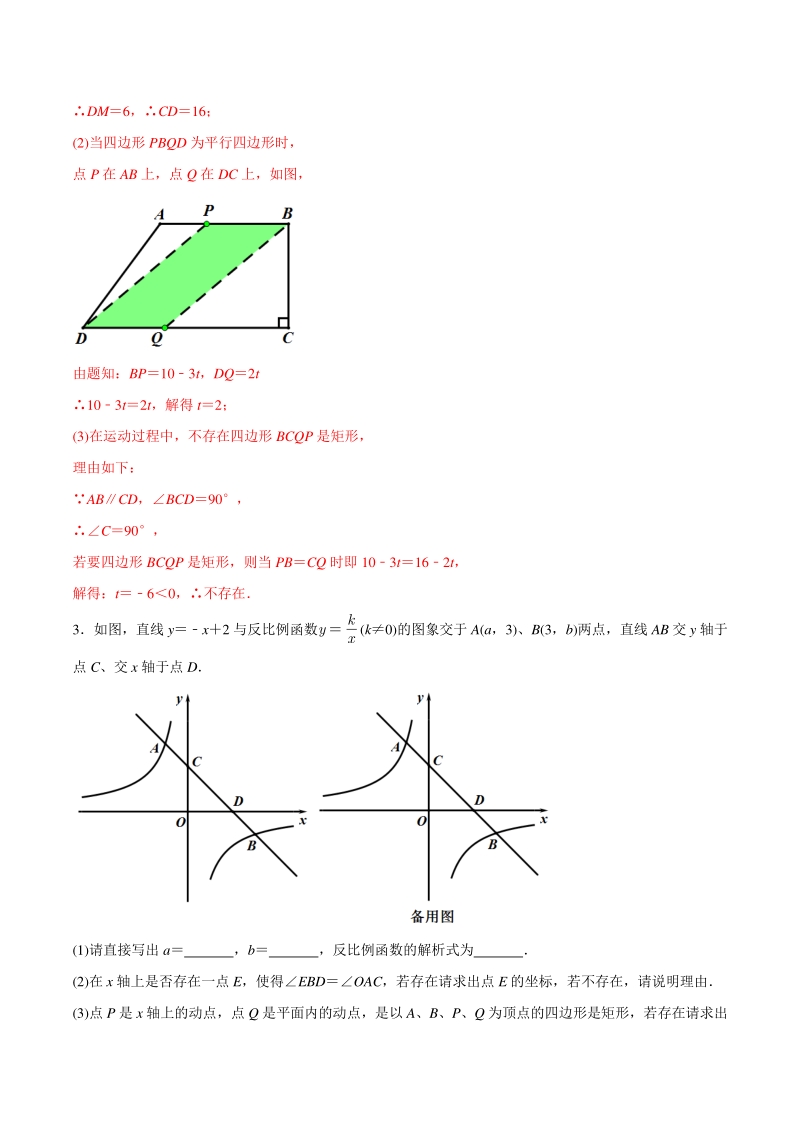
3、6 ODEDEOADF26.6 DOE180OEDODE18026.626.6126.8127 即当直线 DB 绕点 O 约顺时针旋转 127时，四边形 CDBE 是矩形 2 如图 1，在四边形 ABCD 中，ABCD，BCD90，ABAD10cm，BC8cm点 P 从点 A 出发， 以每秒 3cm 的速度沿线段 AB 方向向 B 运动，点 Q 从点 D 出发，以每秒 2cm 的速度沿线段 DC 方向向点 C 运动已知动点 P、Q 同时出发，当点 P 运动到点 B 时，P、Q 同时运动停止，设运动时间为 t 秒 (1)求 CD 的长； (2)当 t 为何值时，四边形 PBQD 为平行四边形？

4、(3)在运动过程中，是否存在四边形 BCQP 是矩形？若存在，请求出 t 的值；若不存在，请说明理由 【解答】(1)CD16；(2)t2；(3)不存在 【解析】(1)过点 A 作 AMCD 于 M，如图所示： 根据勾股定理，AD10，AMBC8， DM6，CD16； (2)当四边形 PBQD 为平行四边形时， 点 P 在 AB 上，点 Q 在 DC 上，如图， 由题知：BP103t，DQ2t 103t2t，解得 t2； (3)在运动过程中，不存在四边形 BCQP 是矩形， 理由如下： ABCD，BCD90， C90， 若要四边形 BCQP 是矩形，则当 PBCQ 时即 103t162t， 解得

5、：t60，不存在 3如图，直线 yx2 与反比例函数(k0)的图象交于 A(a，3)、B(3，b)两点，直线 AB 交 y 轴于 点 C、交 x 轴于点 D (1)请直接写出 a ，b ，反比例函数的解析式为 (2)在 x 轴上是否存在一点 E，使得EBDOAC，若存在请求出点 E 的坐标，若不存在，请说明理由 (3)点 P 是 x 轴上的动点，点 Q 是平面内的动点，是以 A、B、P、Q 为顶点的四边形是矩形，若存在请求出 点 Q 的坐标，若不存在请说明理由 【解答】a1，b1，；(2)E 坐标为(0，0)或(，0)；(3)Q 坐标(0，4)或(0，4)或(1， 2)或(1，2) 【解析】(

6、1)A(a，3)、B(3，b)两点在 yx2 上，a1，b1， A(1，3)，(3，1)， A(1，3)在上，k3 反比例函数的解析式为； (2)如图，连接 OB A(1，3)，B(3，1)，OAOB，OACOBD， 当点 E 与 O 重合时，EBDOAC，此时 E(0，0) 作 BEOA，则EBDOAC， 由题意 D(2，0)， BEOA， ， 综上所述，满足条件的点 E 坐标为(0，0)或(，0)； (3)存在如图： 当四边形 AP1Q1B 是矩形时，易知 P1(4，0)， 点 B(3，1)向左平移 3 个单位，向下平移 3 个单位得到 Q1(0，4)； 当四边形 BP2Q2A 是矩形时，

7、P2(4，0)， 点 A(31)向右平移一个单位，向上平移一个单位得到 Q2(0，4) 当 AB 是矩形的对角线时，设 AB 的中点为 R(1，1)，设 P3(m，0)， RP2，(1m)212(2)2，m1或 1， P3(1，0)，P4(1，0)， Q3(1，2)，Q4(1，2)， 综上所述，满足条件的点 Q 坐标(0，4)或(0，4)或(1，2)或(1，2) 4 如图，抛物线 yax2bx5 经过点 A(1，0)，B(2，5)，抛物线与 x 轴的另一个交点为 C 点，点 P 为 y 轴上一动点，作平行四边形 BPCD (1)求 C 点的坐标； (2)是否存在 P 点，使四边形 BPCD 为

8、矩形？若存在，求出 P 点坐标；若不存在，请说明理由； (3)连结 PD，PD 的长度是否存在最小值？若存在，求出最小值；若不存在，请说明理由； (4)若 E 为 AC 中点，求抛物线上满足到 E 点的距离小于 2 的所有点的横坐标 x 的范围 【解答】(1)C(3，0)；(2)点 P 的坐标为(0，2)或(0，3) 【解析】解：(1)抛物线 yax2bx5 经过点 A(1，0)，B(2，5)， ，解得， ， 当 y0 时， 解得 x11，x23，C 点的坐标为(3，0)； (2)设抛物线与 y 轴交于点 F，则 F 点坐标为(0，5)，连接 BF，如图所示： B(2，5)，BFP90，四边形

9、 BPCD 为矩形，BPC90， BPFOPC90， OPCPCO90，BPFPCO 在BPF 与PCO 中， ，BPFPCO， ， B(2，5)，F(0，5)，C(3，0)， BF2，OC3，OF5， PF5OP， 整理得，OP25OP60，解得 OP2 或 OF3， 点 P 的坐标为(0，2)或(0，3)； (3)连接 BC，设 PD、BC 相交于点 H，如图所示： 四边形 BPCD 是平行四边形，PD、BC 互相平分，PD2PH， 又C(3，0)，B(2，5)， 点 H 的坐标为(2.5，2.5)， 根据垂线段最短，PHy 轴时，PH 最短，此时，PH2.5，PD2PH22.55； (4

10、)抛物线解析式为， E 为 AC 中点，点 E 的坐标为(1，0)， 以 E 为圆心，以 2 为半径的圆为(x1)2y24， 与抛物线解析式联立消掉(x1)2得， 整理得，5y23y0， 解得 y10， y时， 整理得，(x1)2， 解得 x1，x2， 故当1x或x3 时，抛物线上的点到 E 点的距离小于 2 5 如果一条抛物线 yax2bxc(a0)与 x 轴有两个交点，那么以该抛物线的顶点和这两个交点为顶点 的三角形称为这条抛物线的“抛物线三角形” (1)“抛物线三角形”一定是 三角形； (2)若抛物线抛物线 m：ya(x2)2b(ab0)的“抛物线三角形”是直角三角形，请求出 a，b 满

11、足的关系 式； (3)如图，OAB 是抛物线 n：yx2bx(b0)的“抛物线三角形” ，是否存在以原点 O 为对称中心的 矩形 ABCD？若存在，求出过 O、C、D 三点的抛物线的表达式；若不存在，说明理由 【解答】(1)等腰；(2)ab1；(3) 【解析】(1)抛物线与 x 轴有两个交点关于抛物线的对称轴对称， “抛物线三角形”是等腰三角形； (2)ya(x2)2b(ab0)的“抛物线三角形”是直角三角形， 此“物线三角形”是等腰直角三角形，抛物线的顶点坐标为(2，b)， 把 y0 代入 ya(x2)2b 得 a(x2)2b0，解得， 抛物线 ya(x2)2b(ab0)与 x 轴两交点的坐

12、标为 抛物线 ya(x2)2b(ab0)与 x 轴两交点之间的线段长， ，ab1； (3)存在作 AHOB 于 H 点，如图， 把 y0 代入 yx2bx 得x2bx0，解得 x10，x2b， B 点坐标为(b，0)， ，A 点坐标为， 矩形 ABCD 以原点 O 为对称中心， OAOBOCOD，OAB 为等边三角形， ，解得， A 点坐标为，B 点坐标为， C 点坐标为，D 点坐标为， 设过 O、C、D 三点的抛物线的解析式为， 把 C代入得，解得 a1， 所求抛物线的表达式为 6 如图，已知经过坐标原点的P 与 x 轴交于点 A(8，0)，与 y 轴交于点 B(0，6)，点 C 是第一象限

13、内P 上一点，CBCO，抛物线 yax2bx 经过点 A 和点 C (1)求P 的半径； (2)求抛物线的解析式； (3)在抛物线上是否存在点 D，使得点 A、点 B、点 C 和点 D 构成矩形？若存在，直接写出符合条件的点 D 的坐标；若不存在，试说明理由 【解答】(1)P 的半径是 5；(2)；(3)D(1，3) 【解析】(1)连接 AB，如图所示： AOB90，AB 是P 的直径， 点 A(8，0)，B(0，6)，AO8，BO6， ，P 的半径是 5； (2)作 CHOB，垂直为 H，如图所示： CBCO，H 是 OB 的中点，CH 过圆心 P，C 的坐标是(9，3)， 把 A、C 坐标

14、分别代入 yax2bx 得： ，解得：， 抛物线的解析式为：； (3)设直线 AC 的解析为 ykxc， A(8，0)，C(9，3)， ，解得：， 直线 AC 的解析为 y3x24， 点 A、点 B、点 C 和点 D 构成矩形，BDAC， 设 BD 解析式为 y3xd，直线 BD 过 B 点，d6， BD 解析式为：y3x6， 将 y3x6 与联立得：3x6， 解得；x11，x218(不合题意)， 当x1 时，y3，D(1，3) 7 如图，抛物线 yx2bxc 交 x 轴于点 A，B，交 y 轴于点 C点 B 的坐标为(3，0)，点 C 的坐标为 (0，3)，点 C 与点 D 关于抛物线的对称

15、轴对称 (1)求抛物线的解析式； (2)若点 P 为抛物线对称轴上一点，连接 BD，以 PD，PB 为边作平行四边形 PDNB，是否存在这样的点 P， 使得平行四边形 PDNB 是矩形？若存在，请求出 tanBDN 的值；若不存在，请说明理由. 【解答】(1)yx22x3；(2)tanBDN1 或 【解析】(1)把 B 点坐标、点 C 点坐标为代入抛物线 yx2bxc 方程， 解得，抛物线方程为：yx22x3； 点 A 坐标为(1，0)，点 D 坐标为(2，3)，函数的对称轴为 x1； (2)存在设点 P(1，m)， 设函数对称轴交 x 轴于点 N，过点 D 作 DMPN 于点 M，如图所示：

16、 则MDPBPN，则 tanMDPtanBPN， 即：，解得：m1 或 m2； 则点 P(1，1)或(1，2)，则：PD或，则 PB2或， tanBDN1 或. 8 如图，在平面直角坐标系中，点 A，B 的坐标分别是(5，0)，(0，5)，动点 P 从点 O 出发，沿 x 轴正 方向以每秒 1 个单位的速度运动，同时动点 C 从点 B 出发，沿射线 BO 方向以每秒 1 个单位的速度运动， 以 CP，CO 为邻边构造平行四边形 PCOD在线段 OP 延长线上一动点 E，且满足 PEAO (1)当点 C 在线段 OB 上运动时，求证：四边形 ADEC 为平行四边形； (2)点 P 在运动过程中，

17、 是否存在某个时刻 t(秒)， 使得四边形 ADEC 是矩形？若存在， 求 t 的值； 若不存在， 请说明理由 【解答】(1)见解析；(2)当 t0 或 t15 时，四边形 ADEC 是矩形 【解析】(1)证明：连接 CD 交 AE 于 F，如图所示： 四边形 PCOD 是平行四边形，CFDF，OFPF， PEAO，AFEF，又 CFDF， 四边形 ADEC 为平行四边形； (2)存在， 理由：当四边形 ADEC 是矩形时，ACE90， OCAE，ACOCEO， ， 点 A，B 的坐标分别是(5，0)，(0，5)， OAOB5，OC5t，OE5t， ，解得：t0 或 t15， 当 t0 或 t

18、15 时，四边形 ADEC 是矩形 9 如图，在菱形 ABCD 中，AB4cm，BAD60动点 E、F 分别从点 B、D 同时出发，以 1cm/s 的 速度向点 A、C 运动，连接 AF、CE，取 AF、CE 的中点 G、H，连接 GE、FH设运动的时间为 ts(0t 4) (1)求证：AFCE； (2)试探究：是否存在某个时刻 t，使四边形 EHFG 为矩形，若存在，求出 t 的值，若不存在，请说明理由 【解答】(1)见解析；(2)不存在 【解析】(1)证明： 动点 E、F 同时运动且速度相等，DFBE， 四边形 ABCD 是菱形， BD，ADBC，ABDC， 在ADF 与CBE 中，ADF

19、CBE， DFABEC， ABDC，DFAFAB， FABBEC，AFCE； (2)不存在，假设存在某个时刻 t，使四边形 EHFG 为矩形， 四边形 EHFG 为矩形， EFGH， EF2GH2，即(22t)2(2)2(4t)2， 解得 t0，0t4， 与原题设矛盾，不存在某个时刻 t，使四边形 EHFG 为矩形 10如图，在矩形 ABCD 中，AB16cm，AD6cm，动点 P、Q 分别从 A、C 同时出发点 P 以每秒 3cm 的 速度向 B 移动，一直达到 B 止，点 Q 以每秒 2cm 的速度向 D 移动 (1)P、Q 两点出发后多少秒时，四边形 PBCQ 的面积为 36cm2； (2)P、Q 两点出发后多少秒时，四边形 PBCQ 是矩形. 【解答】(1)t4；(2)t 【解析】(1)在矩形 ABCD 中，CDAB16，BCAD6， 由运动知，AP3t，CQ2t， BPABAP163t， 四边形 PBCQ 的面积为 36cm2， (163t2t)636，t4， P、Q 两点出发后 4 秒时，四边形 PBCQ 的面积为 36cm2； (2)四边形 PBCQ 是矩形， BPCQ，163t2t， t，P、Q 两点出发后秒时，四边形 PBCQ 是矩形.