专题13 二次函数中的图形运动最值问题（教师版含解析）-2021年中考数学复习重难点与压轴题型专项训练

《专题13 二次函数中的图形运动最值问题（教师版含解析）-2021年中考数学复习重难点与压轴题型专项训练》由会员分享，可在线阅读，更多相关《专题13 二次函数中的图形运动最值问题（教师版含解析）-2021年中考数学复习重难点与压轴题型专项训练（60页珍藏版）》请在七七文库上搜索。

1、备战备战 2021 年中考复习重难点与压轴题型专项训练年中考复习重难点与压轴题型专项训练 专题 13 二次函数中的图形运动最值问题 【专题训练】 一、解答题一、解答题 1(2020 浙江绍兴市 九年级其他模拟)已知：如图，ABC 是等腰直角三角形， 90 ,3cmAABAC ，动点 P， Q 同时从 A，B 两点出发，分别沿 AB，AB 方向匀速移动，P 的速度是1cm/s，Q 的速度是 2cm/s，当点 P 到达点 B 时， P，Q 两点停止运动，设点 P 的运动时间为(s)t，解答下列问题： (1)当 t 为何值时，PBQ是直角三角形？ (2)问：是否存在某一时刻 t，使四边形 APQC

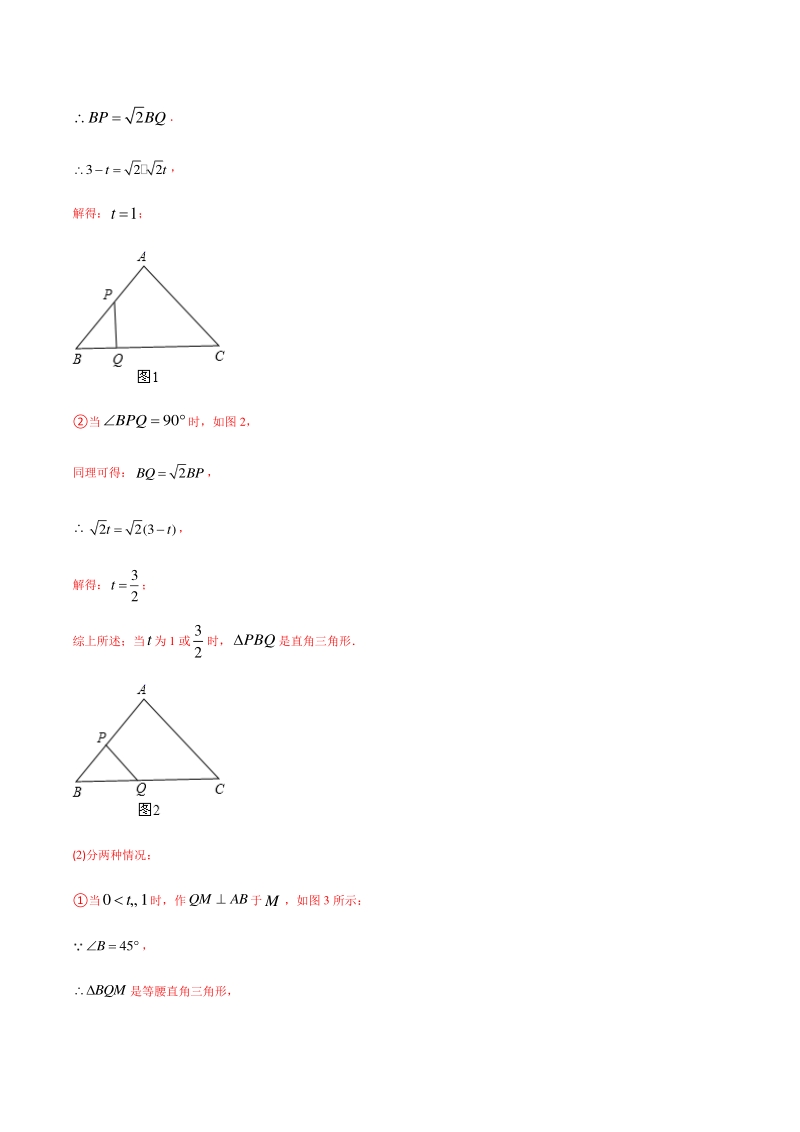
2、的面积与PBQ面积差最小？如果存在，求出相应的 t 值；不存在，说明理 由； (3)设 PQ 的长为(cm)y，试确定 y 与 t 之间的关系式；写出当 t 分别为何值时，PQ 达到最短和最长，并写出 PQ 的最小值 和最大值 【答案】 解：(1)由题可得：90A ，4ABBC，45B ，BQAPt，4BPt 当90PQB 时，如图 1， 45B， BQPQ， 2BPBQ 322tt ， 解得：1t ； 当90BPQ时，如图 2， 同理可得：2BQBP， 22(3)tt， 解得： 3 2 t ； 综上所述；当t为 1 或 3 2 时，PBQ是直角三角形 (2)分两种情况： 当01t 时，作QM

3、 AB于M，如图 3 所示： 45B， BQM是等腰直角三角形， 2 2 QMBMBQt， PBQ的面积 2 1131 (3) 2222 BP QMtttt ， 四边形APQC的面积 ABC 的面积PBQ的面积 22 131139 3 3() 222222 tttt ， 四边形APQC的面积PBQ的面积 22 939 3() 224 ttt，当 3 2 t 时，面积差最小， 但是 3 1 2 t ，不符合题意； 当1t 时，作PMAB于M，如图 4 所示： 45B， BPM 是等腰直角三角形， 22 (3) 22 PMBMBPt， PBQ的面积 2 11231 2(3) 22222 BQ PM

4、tttt， 四边形APQC的面积 ABC 的面积PBQ的面积 22 131139 3 3() 222222 tttt ， 四边形APQC的面积PBQ的面积 22 939 3() 224 ttt， 当 3 2 t 时，面积差最小； 因此，存在某一时刻t，使四边形APQC的面积与PBQ面积差最小， 3 2 t ； (3)根据题意得： 3 1 2 t剟时，存在t的值，使PQ最短， 6 5 t ；理由如下： 如图 3 所示：32PMt，QMt， 由勾股定理得： 2222222 69 (32 )51295() 55 PQPMQMttttt， y= 2 69 5() 55 t ， 当 6 5 t 时，y

5、的最小值 93 5 55 ， 当1t 时， 3 5 2 5 y ； 当 3 2 t 时， 33 5 2 25 y ； 综上所述：当 6 5 t 时，PQ最短，最小值 3 5 5 ； 当P到达B时，Q恰好到达C，此时3t 秒，PQ的最大值 22 333 2BC 【点睛】 本题考查了等腰直角三角形的判定与性质、勾股定理、三角形面积的计算等知识；本题综合性强，难度较大，需要通过作辅 助线进行分类讨论才能得出结果 2(2020 武汉二中广雅中学九年级二模)有一根直尺短边长 4cm，长边长 10cm，还有一块锐角为 45的直角三角形纸板，它的 斜边长为 16cm，如图甲，将直尺的短边 DE 与直角三角形

6、纸板的斜边 AB 重合，且点 D 与点 A 重合将直尺沿射线 AB 方向 平移，如图乙，设平移的长度为 xcm，且满足 0 x12，直尺和三角形纸板重叠部分的面积为 Scm2 (1)当 x0cm 时，S_；当 x4cm 时，S_；当 x12cm 时，S_ (2)当 4x8(如图丙)，请用含 x 的代数式表示 S (3)是否存在一个位置，使重叠部分面积为 28cm2？若存在求出此时 x 的值 【答案】 解：(1)当 x0cm 时，S4428m2； 当 x4cm 时，S88244224cm2； 当 x12cm 时，S4428cm2 故答案为：8cm2；24cm2；8cm2 (2)如图所示：过点 C

7、 作 CMAB 于点 M 当 4x8 时， 梯形 GDMC 的面积 1 2 (GD+CM)DM 1 2 (x+8)(8x) 1 2 x2+32， 梯形 CMEF 的面积 1 2 (EF+CM)ME 1 2 16(x+4)+8(x+4)8 1 2 (20 x)(x4) 1 2 x2+12x40， S梯形 GDMC 的面积+梯形 CMEF 的面积( 1 2 x2+32)+( 1 2 x2+12x40)x2+12x8 (3)当 x4 时，S24cm2， 所以当 S28cm2时，x 必然大于 4，即x2+12x828， 解得 x1x26， 所以当 x6cm 时，阴影部分面积为 28cm2 【点睛】 本

8、题考查了相似形综合题，涉及的知识点有：直角三角形的面积，矩形的性质，梯形的面积，分类思想的应用，方程思想的 应用，综合性较强，解题的关键是对于每个涉及到的知识点和性质较为熟悉，能够灵活运用 3(2020 四会市四会中学九年级二模)如图，在平面直角坐标系中，四边形 OABC 是矩形，OA4，OC3动点 P 从点 C 出 发，沿射线 CB 方向以每秒 2 个单位长度的速度运动；同时，动点 Q 从点 O 出发，沿 x 轴正半轴方向以每秒 1 个单位长度的 速度运动设点 P、Q 的运动时间为 t 秒 (1)当 t2 秒时，求 tanQPA 的值； (2)当线段 PQ 与线段 AB 相交于点 M，且 B

9、M2AM 时，求 t 的值； (3)连结 CQ，当点 P，Q 在运动过程中，记CQPV与矩形 OABC 重叠部分的面积为 S，求 S 与 t 的函数关系式； (4)直接写出OAB 的角平分线经过CQPV边上中点时的 t 值 【答案】 解：(1)当 t2s 时，则 CP224BC，即点 P 与点 B 重合，OQ2，如图 1， AQOAOQ422，且 APOC3， tanQPA 2 3 AQ AP ； (2)当线段 PQ 与线段 AB 相交于点 M，则可知点 Q 在线段 OA 上，点 P 在线段 CB 的延长线上，如图 2， 则 CP2t，OQt， BPPCCB2t4，AQOAOQ4t， PCOA

10、， PBMQAM， BPBM AQAM ，且 BM2AM， 24 4 t t 2，解得 t3， 当线段 PQ 与线段 AB 相交于点 M，且 BM2AM 时，t 为 3s； (3)当 0t2 时，如图 3， 由题意可知 CP2t， SS PCQ 1 2 2t33t； 当 2t4 时，设 PQ 交 AB 于点 M，如图 4， 由题意可知 PC2t，OQt，则 BP2t4，AQ4t， 同(3)可得 24 4 BPBMt AQAMt ， BM 24 4 t t AM， 3AM 24 4 t t AM， 解得 AM 123t t ， SS四边形BCQMS矩形OABCS COQS AMQ34 1 2 t

11、3 1 2 (4t)12 3t t 24 24 t 3t； 当 t4 时，设 CQ 与 AB 交于点 M，如图 5， 由题意可知 OQt，AQt4， ABOC， AMAQ OCOQ ，即 4 3 AMt t ， 解得 AM 312t t ， BM3 312t t 12 t ， SS BCM 11224 4 2tt ； 综上可知 3 02 24 243 24 24 4 tt Stt t t t (4)如图 6， OAD 1 2 OAB45，OA4， D(0，4)， 设直线 AD 解析式为 ykx+b， 代入，得： 40 4 kb b ， 解得 1 4 k b ， 直线 AD 解析式为 yx+4，

12、 由题意知 C(0，3)，P(2t，3)，Q(t，0)， CP 的中点坐标为(t，3)，CQ 中点坐标为( 2 t ， 3 2 )，PQ 中点坐标为( 3 2 t， 3 2 )， 若直线 AD 经过 CP 中点，则t+43，解得 t1； 若直线 AD 经过 CQ 中点，则 2 t +4 3 2 ，解得 t5； 若直线 AD 经过 PQ 中点，则 3 2 t+4 3 2 ，解得 t 5 3 ； 综上，OAB 的角平分线经过 CQP 边上中点时的 t 值为 1 或 5 或 5 3 【点睛】 本题为二次函数与四边形的综合应用，涉及待定系数法、矩形的性质、相似三角形的判定和性质、三角函数的定义、方程思

13、 想及分类讨论思想等知识在(1)中确定 P、B 重合是解题的关键，在(2)中由相似三角形的性质得到关于 t 的方程是解题的关 键，在(3)中确定出 P、Q 的位置，从而确定出 S 为哪一部分图形的面积是解题的关键本题为“运动型”问题，用 t 和速度表示 出相应线段的长度， 化“动”为“静”是解这类问题的一般思路 本题考查知识点较多， 综合性较强， 特别是最后一问， 情况较多， 难度较大 4(2020 揭阳市实验中学九年级期中)如图，已知在 ABC 中，B=90，AB=8cm，BC=6cm P，Q 是 ABC 边上的两个动点， 其中点 P 从点 A 出发沿 AB 方向运动，速度为每秒 1cm，到

14、达点 B 停止运动；点 Q 从点 B 出发沿 BCA 方向运动，速度 为每秒 2cm，到达点 A 停止运动它们同时出发，设出发时间为 t 秒 (1)当 t=_秒时，PQAC； (2)设 PQB 的面积为 S，求 S 关于 t 的函数关系式，并写出自变量的取值范围； (3)当点 Q 在边 CA 上运动时，直接写出能使 BCQ 为等腰三角形的 t 的值 【答案】 解：(1)如图，当 PQAC 时， BQPBCA， BQBP BCAB ，即 28 68 tt ， 解得：t= 24 11 ， 故答案为： 24 11 ； (2)解：当 0t3 时，如图所示： BQ=2t，BP=8-t， 则 S= 1 2

15、 BP BQ = 1 2 (8-t) 2t =-t2+8t， 当 3t8 时，如图所示，过点 Q 作 QHAH 于点 H， HQ= 3 5 (16-2t)， S= 1 2 BP HQ = 13 8t162t 25 = 2 348192 tt 555 ； (3)当 t 为 5.5，6 或 6.6 时， BCQ 为等腰三角形， 当 CQ=BQ 时，如图所示： 则C=CBQ， ABC=90， CBQ+ABQ=90，A+C=90， A=ABQ， BQ=AQ， CQ=AQ=5， BC+CQ=11， t=112=5.5 当 CQ=BC 时，如图所示： 则 BC+CQ=12， t=122=6 当 BC=BQ

16、 时，如图所示、过点 B 作 BEAC 于点 E， 则 BE= 6 8 10AC AB BC =4.8， CE= 22 BCBE =3.6， CQ=2CE=7.2， BC+CQ=13.2， t=13.22=6.6， 综上，当 t 为 5.5，6 或 6.6 时， BCQ 为等腰三角形 【点睛】 本题考查了相似三角形的判定和性质，等腰三角形的性质，函数表达式，解题的关键是根据图形的运动，适当分情况讨论. 5(2020 云南昆明市 九年级其他模拟)矩形管在我们日常生活中应用广泛，石油、天然气的运输，制造建筑结构网架，制造公 路桥梁等领域均有应用如图，若矩形管ABCD的两边长20 ,6 ABcm A

17、Dcm， 1若点PQ分别从AB、同时出发，P在边AB上沿 AB 方向以每秒2cm的速度匀速运动，Q在边BC上沿BC方向以 每秒1cm的速度匀速运动，当一点到达终点时，另一点也停止运动设运动时间为x秒，PBQ的面积为 2 y cm求 PBQ面积的最大值； 2若点P在边AB上，从点A出发，沿AB方向以每秒2cm的速度匀速运动，点Q在边BC上，从BC中点出发， 沿BC方向以每秒1cm的速度匀速运动，当点P运动到AB中点时，点Q开始向上运动，当一点到达终点时，另一点也停 止运动设点P运动时间为t秒，PBQ的面积为 2 mcm 求m与t的函数关系式 【答案】 解： 1由题意得，,2BQx APx 20A

18、B ， 20 2BPABAPx ， 1 2 PBQ SBP BQ =， 1 20) 2 (2yxx， 即 2 )06(01yxxx 2 5)5(2yx ， 10a ，且06,x 当 5x 时，y25 最大值 ， 即PBQ的最大面积是 2 25cm 1 1 2202()()3303 05 2 mttt 2 2 1 202351220 58 2 mttttt m与t的函数关系式为 2 303 05 1220 58 tt m ttt 【解答】 本题考查了矩形的性质，二次函数的最值问题，根据题意表示出 PB、BQ 的长度是解题的关键 6(2020 银川唐徕回民中学九年级二模)如图，在锐角三角形 ABC

19、 中，BC=12， ABC 的面积为 48，D，E 分别是边 AB，AC 上的两个动点(D 不与 A，B 重合)，且保持 DEBC，以 DE 为边，在点 A 的下方作正方形 DEFG (1)当正方形 DEFG 的边 GF 在 BC 上时，求正方形 DEFG 的边长； (2)设 DE=x， ABC 与正方形 DEFG 重叠部分的面积为 y，试求 y 关于 x 的函数关系式，写出 x 的取值范围，并求出 y 的最大 值 【答案】 (1)如图，过点 A 作 ALBC 于 L，交 DE 于 H S ABC= 1 2 BC AL48， AL=8 在正方形 DEFG 中，DEGF ADE=ABC，AED=

20、ACB， 又BAC=BAC ADEABC AHDE ALBC 8 812 DEDE DE= 24 5 (2)如图，过点 A 作 ALBC 于 L，交 DE 于 Q 设 DE 为 x， DEBC，ADE=ABC，AED=ACB， 又BAC=BAC ADEABC AQDE ALBC 8 812 QLDE QL= 2 8 3 x y=DEQL=x( 2 8 3 x) = 2 3 (x-6)2+24 (0 x 12 ) 当 x=6 时，y 的最大值为 24 【点睛】 本题考查三角形与矩形的动点问题，判定三角形相似并利用三角形相似的性质得到有关比例式是解题关键 7(2020 广东惠州市 九年级二模)如图

21、 1，已知 Rt ABC 中，10ABcm，6BCcm，点P由点B出发沿BA方向 向点A匀速运动， 同时点Q由点A出发沿AC方向向点C匀速运动， 速度均为2/cm s， 连接PQ， 设运动的时间为t(单 位：s)04t 图 1 图 2 (1)当/ /PQBC时，t _s； (2)设AQP的面积为S(单位： 2 cm )，当t为何值时，S取得最大值，并求出最大值； (3)如图 2， 取点Q关于AP的对称点 Q ， 连接 AQ ， PQ ， 得到四边形AQPQ， 是否存在某一时刻t， 使四边形AQPQ 为菱形？若存在，求出此时菱形的面积；若不存在，请说明理由 【答案】 解：(1)由已知，有 AC=

22、 22 8ABBC ， 如果/ /PQBC，则有APQABCV: V， APAQ ABAC ，即 1022 108 tt ，可以解得： 20 9 t ， 故答案为 20 9 (2)如图，过点P作PDAC于点D， /PDBC， APPD ABBC 即 102 106 tPD ， 解得 6 6 5 PDt 1 2 AQP SAQ PD 16 26 25 tt 2 6 6 5 tt 2 6515 522 t 当 5 2 ts时， AQP S取得最大值，最大值为 2 15 2 cm (3)假设存在某一刻t，使四边形AQPQ为菱形，则有2AQPQBPt，如图，过点P作PDAC于点 D，则 有/PDBC，

23、 APPDAD ABBCAC ， 即 102 1068 tPDAD 解得 6 6 5 PDt， 8 8 5 ADt 818 828 55 QDADAQttt， 在Rt PQD中，由勾股定理得 222 QDPDPQ， 即 22 2 186 86(2 ) 55 ttt ， 化简得 2 13901250tt ， 解得 1 5t ， 2 25 13 t ， 04t ， 25 13 t ，由(2)可知， 2 6 6 5 AQP Stt ， 2 6 226 5 AQPAQPQ SStt 菱形 2 2 625252400 26 51313169 cm 当 25 13 ts时，四边形AQPQ为菱形，此时菱形的

24、面积为 2 2400 169 cm 【点睛】 本题考查相似三角形、 二次函数、 勾股定理的综合应用， 在解题中利用数形结合思想把几何问题转化为函数求解是解题关键 8(2020 新疆和田地区 九年级二模)如图，在矩形ABCD中，6,12ABBC，点P从点A出发沿AB边向点B以 1 个单位每秒的速度移动，同时点Q从点B出发沿BC边向点C以 2 个单位每秒的速度移动。如果,P Q两点在分别到达 ,B C两点后就停止移动，设运动时间为t秒06t ，回答下列问题： (1)运动开始后第几秒时，PBQ的面积等于8； ()设五边形APQCD的面积为S，写出S与t的函数关系式，当t为何值时S最小？求S的最小值

25、【答案】 (1)由题知 PB=6-t，BQ=2t， PBQ的面积等于8，则 1 628 2 tt， 解得 12 2,4tt， 则运动开始后第 2 秒或第 4 秒时，PBQ的面积等于8； (2)由题知矩形ABCD减去PBQ的面积即为五边形APQCD的面积， 1 S=6 1262 2 tt 2 =672tt 2 =363t 当 t=3 时，S 有最小值 63. 【点睛】 本题考查了二次函数的最值在解决面积问题中的运用关键是根据 t，表示相关线段的长度，再计算面积，把所得的代数式看作 二次函数求最值 9(2020 苏州市吴江区南麻中学)(本题满分 10 分)如图，在 ABC 中，ACB90，BC3c

26、m动点 Q 以 1cm/s 的速度在 ABC 的边上按 ABC 的路线匀速移动，当点 Q 到达 C 点时停止移动，动点 P 在 ABC 的边上按 CA 的路线匀速移动， 当点 P 到达 A 点时停止移动已知点 P、点 Q 同时开始移动，同时停止移动(即同时到达各自的终止位置)设动点 P 移动的 时间为 t(s)， APQ 的面积为 S(cm2)，S 与 t 的函数关系如图所示 (1)图中 AB cm，图中 n cm2； (2)求 S 与 t 的函数表达式，并求 S 的最大值； (3)当 t 为何值时， APQ 为等腰三角形 【答案】 (1)5t 时， 点 Q 与点 B 重合，5ABcm， 根据

27、勾股定理可得 22 534AC ， 点 Q 运动的总时间为(53) 18 秒， 由于两点同时停止移动， 所以点 P 运动的速度为4 80.5 cm/s， 所以4 0.5APt ， 当点 Q 在 AB 上时，AQt， 作QHAC于 H，如图，易证AQHABC，则 35 QHt ，得 3 5 QHt，所以 2 3136 (40.5 ) 52205 Stttt ，当5t 时， 9 n 4 ， 故答案为 AB5cm， 9 n 4 cm22 分 (2)当点 Q 在 AB 上时，05t ， 由(1)知 2 36 205 Stt ，当4t 时， 12 5 S 最大 ；4 分 当点 Q 在 BC 上时，58t

28、 ，如图，8CQt， 2 1 (8)(40.5 )(40.5 ) 2 Sttt，故答案为 2 2 36 05 205 (40.5 )58 ttt S tt 当 当 ，最大值为12 5 ；6 分 (3)当点 Q 在 AB 上时，05t ，若 AQ=PQ，如图，QHAC于 H，易证AQH ABC ，则 45 AHt ， 得 4 5 AHt，AQ=PQ，QHAC，AP=2AH， 14 4 25 tt，解得 40 13 t ；7 分 若 AP=PQ，如图，作PMAB于 M，又AP=PQ，AQ=2AM，易证APMABC，则 1 4 2 1 5 4 2 t t ，解得 32 9 t ；8 分 若 AP=A

29、Q，则 1 4 2 tt，解得 8 3 t ；9 分 当点 Q 在 BC 上时，58t ，如图， 1 4 2 APPQt，8CQt， 1 2 CPt， 222 CQCPPQ， 222 11 (8)()(4) 22 ttt，化简得 2 12480tt ，方程无解；故答案为 40 13 t 或 32 9 或 8 3 10 分 图 图 图 考点：函数，相似，勾股定理，分类思想 10(2020 吉林延边朝鲜族自治州 九年级一模)如图，在 Rt ABC 中，C=90，AC=2cm，AB=4cm点 P 从点 A 出发，沿 AB 以 1cm/s 的速度向终点 B 运动当点 P 与点 A、B 不重合时，过点

30、P 作 PQAB 交射线 AC 于点 Q，以 AP，AQ 为邻边向上 作平行四边形 APMQ设点 P 的运动时间为 x(s)，解答下列问题 (1)A= ； (2)当点 M 在 BC 上时，x 的值为 ； (3)设平行四边形 APMQ 与 ABC 的重叠部分图形的面积为 y(cm2)，求 y 与 x 之间的函数关系式； (4)整个运动过程中，直接写出 ABM 为直角三角形时 x 的值 【答案】 (1)如图中， 在 Rt ABC 中，ACB=90，AC=2cm，AB=4cm， cosA= 1 = 2 AC AB ， A=60， 故答案为：60 (2)如图 2 中，当点 M 落在 BC 上时， 由题

31、意知，PA=xcm， 四边形 APMQ 是平行四边形， PM=AQ=2AP=2x， PMAC， = PMBP BCBA ， 24 = 24 xx ， x= 4 5 故答案为： 4 5 (3)如图 1 中，当 0 x 4 5 时，重叠部分是平行四边形 APMQ， 在 Rt APQ 中，AQP=30，AP=x， AQ=2x，PQ= 3x， y=SAPMQ=APPQ= 3x 2 如图 3 中，当 4 5 x1 时，重叠部分是五边形 APEFQ，AP=x， AQ=PM=2x，PB=4x， PE= 1 2 (4x) EM=PMPE=2x 1 2 (4x)= 5 2 x2， EF= 3( 5 2 x2)

32、y=SAPMQS EFM= 3x 21 2 3( 5 2 x2)2=17 3 8 x2+5 3x23 如图 4 中，当 1x4 时，重叠部分是四边形 APEB，AP=x， AQ=2x，BP=4x， PE= 1 2 (4x) BE= 3 2 (4x)， CE=2 3 3 2 (4x)= 3 2 x y=S四边形ACEP= 1 2 (PE+AC)CE= 1 2 1 2 (4x)+2 3 2 x= 3 8 x2+ 3x 综上所述，y= 2 2 2 4 30 5 17 34 5 32 31 85 3 3(14) 8 xx xxx xxx (4)如图 5 中，当AMB=90时，设 PQ 交 AM 于 F

33、， PAF=BAM，APF=AMB=90， APFAMB， = APAF AMAB ， PA=x，PQ= 3x，PF=FQ= 3 2 x， AF= 2 222 37 = 22 PAPFxx x， 四边形 APMQ 是平行四边形， AM=2AF= 7x， 7 2 = 47 x x x ， x= 8 7 ，0 x(舍去) 如图 6 中，当ABM=90时，设 AM 交 PQ 于 F APF=ABM=90， PFBM， AF=FM， AP=PB=2， x=2， 综上所述，满足条件的 x 的值为 8 7 或 2 【点睛】 本题属于四边形综合题，考查了平行四边形的性质，相似三角形的判定和性质，三角形中位线

34、定理，解直角三角形，多边形 的面积等知识，解题的关键是灵活运用所学知识解决问题，学会用分类讨论的思想思考问题，属于中考压轴题 11(2020 吉林长春市 九年级一模)如图，在Rt ABC中，90ACB，12AC ，20AB 点P从点B出发， 以每秒 5 个单位长度的速度沿BC向终点C运动，同时点M从点A出发，以相同的速度沿AB向终点B运动，过点P作 PQAB于点Q，连结PQ，以PQ、MQ为邻边作矩形PQMN，当点P运动到终点时，整个运动停止，设矩形 PQMN与 ABC重叠部分图形的面积为 (0)S S ，点P的运动时间为t秒 (1)BC的长为 ； 用含t的代数式表示线段PQ的长为 ； (2)当

35、QM的长度为 10 时，求t的值； (3)求S与t的函数关系式； (4)当过点Q和点N的直线垂直于RtABC的一边时，直接写出t的值 【答案】 (1)ACB90，AC12，AB20， BC 2 2 ABAC 400 144 16， 故答案为：16； sinB ACPQ ABBP ， 12 205 PQ t ， PQ3t， 故答案为：3t； (2)当 20 0 9 t 时，可列20910t， 10 9 t ，符合题意 当 2016 95 t 时，可列92010t ， 1016 35 t ，不符合题意，故舍去 综上，当QM的长度为 10 时，t的值为 10 9 (3)如图 1，当 20 0 9 t

36、 时， 2 3 (209 )2760Stttt 如图 2，当 2016 95 t 时， 2 3 3(205 ) (920) 274 75150 28 ttt stt (4)如图，若 NQAC， NQBC， BMQN， tanBtanMQN， ACMN BCMQ ， 12 16 3 209 t t ， t 20 13 ， 如图，若 NQBC， NQAC， ABQN， tanAtanBQN， BCMN ACQM ， 163 12920 t t ， t 80 27 综上所述：当 t 20 13 或 80 27 时，过点 Q 和点 N 的直线垂直于 Rt ABC 的一边 【点睛】 本题是四边形综合题，

37、考查了矩形的性质，勾股定理，锐角三角函数等知识，利用分类讨论思想解决问题是本题的关键 12(2020 广东广州市 九年级一模)如图，在 ABC 中，A90，AB3，AC4，点 M、Q 分别是边 AB、BC 上的动点(点 M 不与 A、B 重合)，且 MQBC，过点 M 作 MNBC交 AC 于点 N，连接 NQ，设 BQx (1)是否存在一点 Q，使得四边形 BMNQ 为平行四边形，并说明理由； (2)当 BM2 时，求 x 的值； (3)当 x 为何值时，四边形 BMNQ 的面积最大，并求出最大值 【答案】 解：(1)存在，理由如下： MNBC， AMNABC， AM MN AB BC 3

38、5 ， 设 AM3a，则 MN5a， BQMN5a， MNBQ， NMQMQB90， AMN+BMQ90， 又B+BMQ90， BAMN， 又MQBA90， MBQNMA， AM BQ MN BM ，即 3 5 a a 5 33 a a ， 解得 a 9 34 ， BQ 45 34 ， MNBQ， 当 BQMN 45 34 ，四边形 BMNQ 为平行四边形； 当 BQMN 时，四边形 BMNQ 为平行四边形， (2)BQMA90，BB， BMQBCA， BM BC BQ BA ，即 2 5 3 x ， 解得 x 6 5 ； (3)A90，AB3，AC4， BC 22 ABAC 5， QBMAB

39、C， QB AB QM AC BM BC ，即 3 x 4 QM 5 BM ， 解得，QM 4 3 x，BM 5 3 x， MNBC， MN BC AM AB ，即 5 MN 5 3 3 3 x ， 解得，MN5 25 9 x，则四边形 BMNQ 的面积 1 2 (5 25 9 x+x) 4 3 x 32 27 (x 45 32 )2+ 75 32 ， 当 x 45 32 时，四边形 BMNQ 的面积最大，最大值为 75 32 【点睛】 本题属于四边形综合题，主要考查了平行四边形的判定、相似三角形的判定与性质、勾股定理以及二次函数的应用，掌握三 角形相似的判定和性质是解答本题的关键 13(20

40、20 山东青岛市 九年级二模)如图，在菱形 ABCD 中，AB=5cm，BD=8cm点 P 从点 B 出发，沿 BA 方向匀速运动，速 度为1/cm s；同时，点 Q 从点 D 出发，沿 DA 方向匀速运动，速度为 1cm/s过点 P 作 PNBC 分别交 BD，CD 于点 M,N， 连接 QM，QN设运动时间为 05t st 解答下列问题： (1)当t为何值时，点P在线段QN的垂直平分线上？ (2)设QMN的面积为 2 y cm，求y与t的函数关系式； (3)在运动过程中，是否存在某一时刻t，使QMN的面积为菱形ABCD面积的 2 25 ，若存在，求出t的值；若不存在， 请说明理由； (4)

41、是否存在某一时刻t，使QMN为等腰三角形？若存在，请直接写出t的值；若不存在，请说明理由 【答案】 解：(1)连接PQ 5APAQt APAQ ABAD AA APQABD APPQ ABBD 5 58 tPQ 8 8 5 PQt 若点P在线段QN的垂直平分线上 PQPN 8 85 5 t 15 8 t 当 15 8 t 时，点P在线段QN的垂直平分线上 (2)过点A作AFBC，垂足为F，交PN于点E /PNBC AEPN 连接AC，交BD于点O，根据题意3OA， 6AC 菱形面积： 11 6 85 22 AF 24 5 AF 90AEPAFB，PAEBAF AEPAFB APAE ABAF

42、5 24 5 5 tAE 2424 525 AEt /ADPN QMN的高等于AE 四边形ABCD是菱形 PMBPt， 5MNt 12424 (5) 2525 ytt 2 1224 12 255 tt y与t的函数关系式是 2 1224 12(05) 255 yttt (3)假设存在某一时刻t，使QMN的面积为菱形ABCD面积的 2 25 ， 则 2 122421 126 8 255252 tt 解得， 1 3t ， 2 7t (不合题意，舍去) 答：当3t 时，QMN的面积为菱形ABCD面积的 2 25 (4)若QMQN时， 由(2)得 2424 55 AEt 由题意得，PMt，5 tMN

43、过 Q 作QGEN于点 G， QMQN，QGEN 15 22 t MGGNMN 在Rt MQG中， 222 MQMGQG 2424 55 QGAEt 2 2 52424 255 t tt 195 89 t ； 若QNMN时， 过 N 作NJMQ于 J，如图， 则 22 NJMNMJ ， 1 2 QMN SNJMQ 而 2 1224 12 255 QMN Stt 70 39 t ； 若QMMN时，5tt ， 5 2 t 【点睛】 本题综合考查了菱形的性质，三角形相似的判定与性质，垂直平分线的性质以及勾股定理的应用，本题综合性强，有一定难 度 14(2020 广东佛山市 九年级三模)如图 1，矩形

44、 OABC 的顶点 O 是直角坐标系的原点，点 A、C 分别在 x 轴、y 轴上，点 B 的坐标为(8，4)，将矩形 OABC 绕点 A 顺时针旋转得到矩形 ADEF，D、E、F 分别与 B、C、O 对应，EF 的延长线恰好经过 点 C，AF 与 BC 相交于点 Q (1)证明： ACQ 是等腰三角形； (2)求点 D 的坐标； (3)如图 2，动点 M 从点 A 出发在折线 AFC 上运动(不与 A、C 重合)，经过的路程为 x，过点 M 作 AO 的垂线交 AC 于点 N，记 线段 MN 在运动过程中扫过的面积为 S；求 S 关于 x 的函数关系式 【答案】 (1)证明：四边形 OABC，

45、四边形 FADE 都是矩形， AOC90，AFEAFC90，BCOA， CFAAOC90，ACAC，AOAF， Rt ACORt ACF(HL)， CAOCAF， BCOA， BCACAO， BCAACF， QCQA， ACQ 是等腰三角形 (2)解：设 CQAQx， B(8，4)， BC8，AB4， 在 Rt AQB 中，AQ2BQ2+AB2， x2(8x)2+42， x5， BQ3， 如图 1 中，过点 D 作 DHx 轴于 H QADBAH90， QABDAH， BAHD90， ABQAHD， ABQBAQ AHDHAD ， 435 4AHDH ， AH16 5 ，DH12 5 ， OH

46、OA+AH8+16 5 56 5 ， D( 56 12 , 55 ) (3)当 0 x8 时，如图 2 中，延长 MN 交 AO 于 H，作 QJAB 交 AC 于 J QJAB， QJCQ ABCB ， 5 48 QJ ， QJ 5 2 ， MNQJ， AMNAQJ， AMMNAH AQQJBQ ， 5 53 2 xMNAH MN 1 2 x，AH 3 5 x ， S 1 2 MNAH 1 2 1 2 x3 5 x 3 20 x2 当 8x12 时，如图 3 中，作 QJAB 交 AC 于 J，作 EKAB 交 BC 于 T，设 MN 交 BC 于 R FKAB，JQAB， FKJQ， AQJAFK， QJAQBQ FKAFBT ， 5 53 2 8FKBT ， FK4，BT 24 5 ， CTBCBT8 24 5 16 5 ， MNFK， CMNCFK， CMMNCR CFFKCT ， 12 16 44 5 xMNCR ， MN12x，CR 4 5 (12x)， SS ACFS AFK 1 2 412 1 2 (12x) 4 5 (12x) 2 248168