2021年中考数学分类专题突破28 四边形中的三角形全等问题（含答案解析）

《2021年中考数学分类专题突破28 四边形中的三角形全等问题（含答案解析）》由会员分享，可在线阅读，更多相关《2021年中考数学分类专题突破28 四边形中的三角形全等问题（含答案解析）（24页珍藏版）》请在七七文库上搜索。

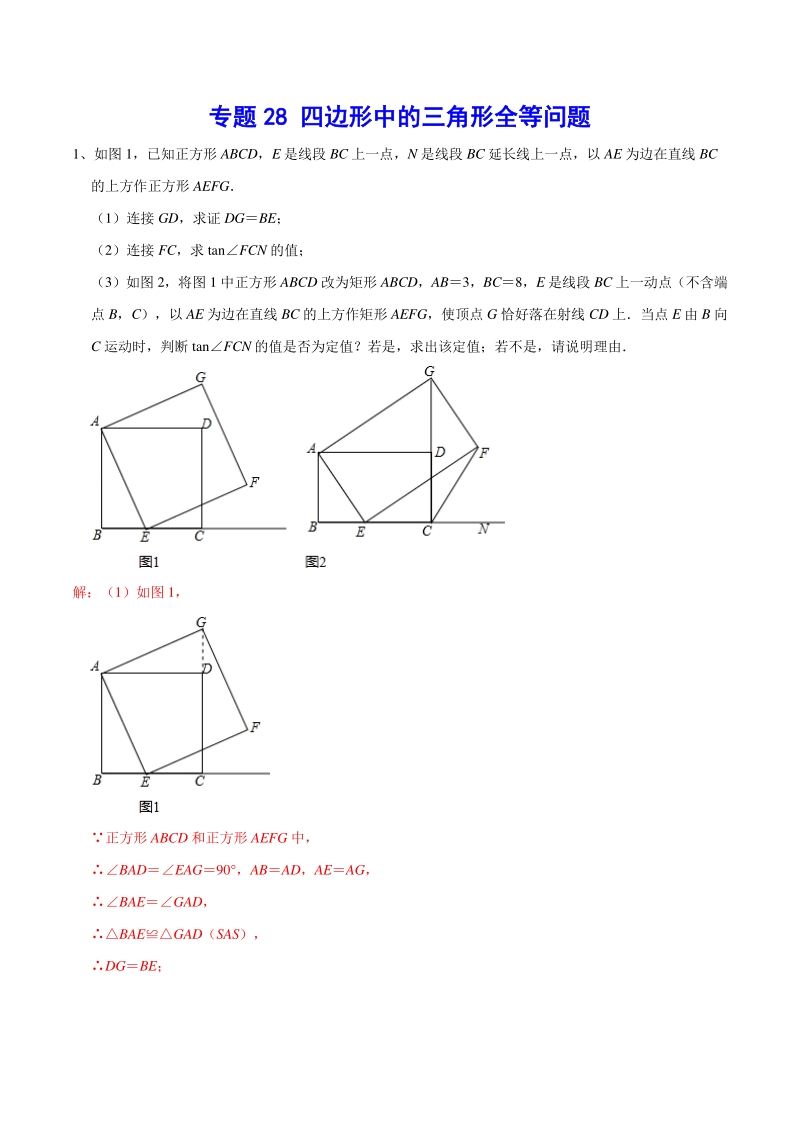
1、专题专题 28 28 四边形中的三角形全等问题四边形中的三角形全等问题 1、如图 1，已知正方形 ABCD，E 是线段 BC 上一点，N 是线段 BC 延长线上一点，以 AE 为边在直线 BC 的上方作正方形 AEFG （1）连接 GD，求证 DGBE； （2）连接 FC，求 tanFCN 的值； （3）如图 2，将图 1 中正方形 ABCD 改为矩形 ABCD，AB3，BC8，E 是线段 BC 上一动点（不含端 点 B，C），以 AE 为边在直线 BC 的上方作矩形 AEFG，使顶点 G 恰好落在射线 CD 上当点 E 由 B 向 C 运动时，判断 tanFCN 的值是否为定值？若是，求出该

2、定值；若不是，请说明理由 解：（1）如图 1， 正方形 ABCD 和正方形 AEFG 中， BADEAG90 ，ABAD，AEAG， BAEGAD， BAEGAD（SAS）， DGBE； （2）如图 2，过点 F 作 FMBN 于 M，则BAEFFME90 ， BAE+AEBFEM+AEB90 ， 即BAEFEM， 又 AEEF， BAEMEF（ASA）， FMBE，EMAB， 又 BE+ECAB，EMEC+CM， CMFM， 在 Rt FCM 中，tanFCN1； （3）如图 2，过点 F 作 FMBN 于 M，则BAEFFME90 ， BAE+AEBFEM+AEB90 ， 即BAEFEM，

3、 同理可证GADFEM， 又 AGEF， DAGMEF， BAEMEF， EMADBC8， 设 BEa，则 EMEC+CMBCBE+EC， CMBEa， ， FM ， tanFCN，即 tanFCN 的值为定值 2、【操作发现】 如图， 在正方形 ABCD 中， 点 N、 M 分别在边 BC、 CD 上， 连结 AM、 AN、 MN MAN45 ， 将 AMD 绕点 A 顺时针旋转 90 ，点 D 与点 B 重合，得到 ABE易证： ANMANE，从而得 DM+BNMN 【实践探究】 （1）在图条件下，若 CN3，CM4，则正方形 ABCD 的边长是 （2）如图，点 M、N 分别在边 CD、A

4、B 上，且 BNDM点 E、F 分别在 BM、DN 上，EAF45 ， 连接 EF，猜想三条线段 EF、BE、DF 之间满足的数量关系，并说明理由 【拓展】 （3）如图，在矩形 ABCD 中，AB3，AD4，点 M、N 分别在边 DC、BC 上，连结 AM，AN，已知 MAN45 ，BN1，求 DM 的长 【实践探究】 （1）解：四边形 ABCD 是正方形， ABCDAD，BADCD90 ， 由旋转得： ABEADM， BEDM，ABED90 ，AEAM，BAEDAM， BAE+BAMDAM+BAMBAD90 ， 即EAM90 ， MAN45 ， EAN90 45 45 ， MANEAN， 在

5、 AMN 和 EAN 中， ， AMNEAN（SAS）， MNEN ENBE+BNDM+BN， MNBN+DM 在 Rt CMN 中，MN5， 则 BN+DM5， 设正方形 ABCD 的边长为 x，则 BNBCCNx3，DMCDCMx4， x3+x45， 解得：x6， 即正方形 ABCD 的边长是 6； 故答案为：6； （2）EF2BE2+DF2， 理由如下：如图，将 AFD 绕点 A 顺时针旋转 90 ，点 D 与点 B 重合，得到 ABH，连结 EH， ADFABH，DFBH，DAFBAH，AHAF， EAF45 ， DAF+BAE45 BAH+BAE， HAE45 EAF， 又AHAF，

6、AEAE， EAHEAF（SAS）， HEEF， BNDM，BNDM， 四边形 BMDN 是平行四边形， DNBM， ANDABM， ADN+AND90 ， ABH+ABM90 HBM， BE2+BH2HE2， EF2BE2+DF2； （3）如图，延长 AB 至 P，使 BPBN1，过 P 作 BC 的平行线交 DC 的延长线于 Q，延长 AN 交 PQ 于 E，连接 EM， 则四边形 APQD 是正方形， PQDQAPAB+BP4， 设 DMx，则 MQ4x， PQBC， ABNAPE， ， PEBN ， EQPQPE4， 由（1）得：EMPE+DM+x， 在 Rt QEM 中，由勾股定理得

7、：（）2+（4x）2（+x）2， 解得：x2， 即 DM 的长是 2 3、如图，将 ABCD 的边 AB 延长到点 E，使 BEAB，连接 DE，交 BC 边于点 F （1）求证： BEFCDF； （2） 连接 BD、 CE， 请探究： 当BFD 与A 之间满足怎样的数量关系时， 能使四边形 BECD 成为矩形？ 为什么？ （1）证明：四边形 ABCD 是平行四边形， ABCD，ABCD BEAB， BECD ABCD， BEFCDF，EBFDCF， 在 BEF 与 CDF 中， ， BEFCDF（ASA）； （2）解：BFD2A 时，四边形 BECD 成为矩形 证明：四边形 ABCD 是平行

8、四边形， ABCD，ABCD，ADCB， ABBE， CDEB， 四边形 BECD 是平行四边形， BFCF，EFDF， BFD2A， BFD2DCF， DCFFDC， DFCF， DEBC， 四边形 BECD 是矩形 4、已知在 ABC 中，ABAC，点 D 在 BC 上，以 AD、AE 为腰做等腰三角形 ADE，且ADEABC， 连接 CE，过 E 作 EMBC 交 CA 延长线于 M，连接 BM （1）求证： BADCAE； （2）若ABC30 ，求MEC 的度数； （3）求证：四边形 MBDE 是平行四边形 （1）证明：ABAC， ABCACB， BAC180 2ABC， 以 AD、A

9、E 为腰做等腰三角形 ADE， ADAE， ADEAED， DAE180 2ADE， ADEABC， BACDAE， BACCADDAECAD， BADCAE， 在 BAD 和 CAE 中， BADCAE（SAS）； （2）解：ABAC， ACBABC30 ， BADCAE， ABDACE30 ， ACBACE30 ， ECBACB+ACE60 ， EMBC， MEC+ECD180 ， MEC180 60 120 ； （3）证明：BADCAE， DBCE，ABDACE， ABAC， ABDACB， ACBACE， EMBC， EMCACB， ACEEMC， MEEC， DBME， 又EMBD，

10、 四边形 MBDE 是平行四边形 5、如图，在四边形 ABCD 中，A90 ，ADBC，BCBD，CEBD，垂足为 E （1）求证： ABDECB； （2）若 AD4，CE3，求 CD 的长 证明：（1）ADBC， ADBEBC， CEBD，A90 ， ABEC90 ， 在 ABD 和 ECB 中， ， ABDECB（AAS）； （2）ABDECB， ABCE3， AD4， 在 Rt ABD 中，由勾股定理可得：BD5， BDECB， DBE4， DEBDBE1， 在 Rt CDE 中，由勾股定理得：CD 6、已知：矩形 ABCD 中，点 E、F 为对角线 AC 上两点，AFCE （1）如图

11、1，求证：BEDF； （2）如图 2，当 ABBEAD 时，连接 DE、BF，在不添加任何辅助线的情况下，请直接写出四个三 角形，使写出的每个三角形的面积都等于矩形 ABCD 面积的 （1）证明：四边形 ABCD 是矩形， ADBC，ADBC， DAFBCE， 在 AFD 和 CEB 中， AFDCEB（SAS）， AFDCEB， BEDF； （2）解： ABF， CDE， ADF， BCE；理由如下： 由（1）得： AFDCEB， 同理： ABFCDE（SAS）， AFD 的面积 CEB 的面积， ABF 的面积 CDE 的面积， 作 BGAC 于 G，如图 2 所示： 四边形 ABCD 是

12、矩形， ABC90 ，BCAD， ABBEAD， ABBEBC， BC2AB，ACAB，AGEG， ABC 的面积AC BGAB BC， BG AB， AG AB， AE2AGAB， AFCE， ABF 的面积 BCE 的面积，CFAEAB， AFACCFABABAB， ABF 的面积AF BGABAB AB2， 矩形 ABCD 的面积AB BCAB 2AB2AB2， ABF 的面积矩形 ABCD 面积的， ABF 的面积 CDE 的面积 ADF 的面积 BCE 的面积矩形 ABCD 面积的 7、如图，在平行四边形 ABCD 中，点 G 在 CD 上，点 H 在 AB 上，且 DGBH，点 E

13、F 在 AC 上，且 AE CF连接 GF，FH，HE，EG （1）求证： CFGAEH； （2）若 AGGC，则四边形 EHFG 是什么特殊四边形？请说明理由 证明：（1）在平行四边形 ABCD 中，ABCD，ABCD， GCFHAE， DGBH， GCAH， 在 CFG 与 AEH 中， CFGAEH（SAS）； （2）CFGAEH， GFEH，AEHGFC， FEHEFG， GFEH， 四边形 EGFH 是平行四边形， AGGC， GAEGCF， 在 GAE 与 GCF 中 ， GAEGCF（SAS）， EGGF， 平行四边形 EGFH 是菱形 8、如图，在 ABC 中，ABAC，AD

14、是 BC 边上的中线，点 E 是 AD 边上一点，过点 B 作 BFEC，交 AD 的延长线于点 F，连接 BE，CF （1）求证： BDFCDE （2）若 DEBC，求证：四边形 BECF 是正方形 （1）证明：AD 是 BC 边上的中线，ABAC， BDCD， BFEC， DBFDCE， BDFCDE， BDFCDE（ASA）； （2）证明：BDFCDE， BFCE，DEDF， BFCE， 四边形 BECF 是平行四边形， ABAC，AD 是中线， 四边形 BECF 是菱形， DEBC，DEDF EF， EFBC， 四边形 BECF 是正方形 9、阅读材料： 教育部基础教育司负责人解读“2

15、020 新中考”时强调要注重学生分析与解决问题的能力，要增强学生的创 新精神和综合素质王老师想尝试改变教学方法，将以往教会学生做题改为引导学生会学习于是她在 菱形的学习中，引导同学们解决菱形中的一个问题时，采用了以下过程（请解决王老师提出的问题）： 先出示问题（1）： 如图 1，在等边三角形 ABC 中，D 为 BC 上一点，E 为 AC 上一点，如果 BDCE，连接 AD、BE，AD、 BE 相交于点 P，求APE 的度数 学习，王老师请同学们说说自己的收获小明说发现一个结论：在这个等边三角形 ABC 中，只要满足 BDCE，则APE 的度数就是一个定值，不会发生改变 紧接着王老师出示了问题

16、（2）： 如图 2，在菱形 ABCD 中，A60 ，E 为 BC 上一点，F 为 CD 上一点，BECF，连接 DE、BF，DE、 BF 相交于点 P，如果 DP4，BP3，求出菱形的边长 问题（3）：通过以上的学习请写出你得到的启示（一条即可） 解：问题（1）ABC 是等边三角形， ABDC60 ，ABBC， 在 ABD 和 BCE 中， ABDBCE（SAS）， BADEBC， APEABP+BAP， APEABP+EBCABC60 ； 问题（2）过点 D 作 DGBF 交 BF 于点 G，如图 2 所示： 四边形 ABCD 是菱形， CA60 ，BCCD， BCD 是等边三角形， BCC

17、DBD， 由（1）可知DPG60 ， 在 Rt DPG 中，sin60 ， 即， 解得：DG2， cos60 ， 即， 解得：PG2， BGBP+PG3+25， 在 Rt BDG 中，由勾股定理得：BD2BG2+DG252+（2）237， BD ， BCBD ， 菱形的边长为 ； 问题（3）平时应该注意基本图形的积累，在学习过程中做个有心人 10、如图 1，在正方形 ABCD（正方形四边相等，四个角均为直角）中，AB8，P 为线段 BC 上一点，连 接 AP，过点 B 作 BQAP，交 CD 于点 Q，将 BQC 沿 BQ 所在的直线对折得到 BQC，延长 QC交 AD 于点 N （1）求证：

18、BPCQ； （2）若 BPPC，求 AN 的长； （3）如图 2，延长 QN 交 BA 的延长线于点 M，若 BPx（0 x8）， BMC的面积为 S，求 S 与 x 之 间的函数关系式 解：（1）证明：ABC90 BAP+APB90 BQAP APB+QBC90 ， QBCBAP， 在 ABP 于 BCQ 中， ， ABPBCQ（ASA）， BPCQ， （2）由翻折可知，ABBC， 连接 BN，在 Rt ABN 和 Rt CBN 中，ABBC，BNBN， Rt ABNRt CBN（HL）， ANNC， BPPC，AB8， BP2CQ，CPDQ6， 设 ANNCa，则 DN8a， 在 Rt N

19、DQ 中，（8a）2+62（a+2）2 解得：a4.8， 即 AN4.8 （3）解：过 Q 点作 QGBM 于 G，由（1）知 BPCQBGx，BMMQ 设 MQBMy，则 MGyx， 在 Rt MQG 中，y282+（yx）2， S BMCS BMQS BCQ ， 11、已知，在 ABC 中，BAC90 ，ABC45 ，点 D 为直线 BC 上一动点（点 D 不与点 B、C 重合）， 以 AD 为边做正方形 ADEF，连接 CF （1）如图，当点 D 在线段 BC 上时，直接写出线段 CF、BC、CD 之间的数量关系 （2）如图，当点 D 在线段 BC 的延长线上时，其他件不变，则（1）中的

20、三条线段之间的数量关系还 成立吗？如成立，请予以证明，如不成立，请说明理由； （3）如图，当点 D 在线段 BC 的反向延长线上时，且点 A、F 分别在直线 BC 两侧，其他条件不变； 若正方形 ADEF 的边长为 4，对角线 AE、DF 相交于点 O，连接 OC，请直接写出 OC 的长度 解：（1）BAC90 ，ABC45 ， ACBABC45 ， ABAC， 四边形 ADEF 是正方形， ADAF，DAF90 ， BAD90 DAC，CAF90 DAC， BADCAF， 在 BAD 和 CAF 中， ， BADCAF（SAS）， BDCF， BD+CDBC， CF+CDBC； 故答案为：C

21、F+CDBC； （2）CF+CDBC 不成立，存在 CFCDBC； 理由：BAC90 ，ABC45 ， ACBABC45 ， ABAC， 四边形 ADEF 是正方形， ADAF，DAF90 ， BAD90 DAC，CAF90 DAC， BADCAF， 在 BAD 和 CAF 中， ， BADCAF（SAS） BDCF BC+CDCF， CFCDBC； （3）BAC90 ，ABC45 ， ACBABC45 ， ABAC， 四边形 ADEF 是正方形， ADAF，DAF90 ， BAD90 BAF，CAF90 BAF， BADCAF， 在 BAD 和 CAF 中， ， BADCAF（SAS）， A

22、CFABD， ABC45 ， ABD135 ， ACFABD135 ， FCD135 45 90 ， FCD 是直角三角形 正方形 ADEF 的边长 4 且对角线 AE、DF 相交于点 O DFAD4，O 为 DF 中点 Rt CDF 中，OCDF 13、已知四边形 ABCD 和四边形 CEFG 都是正方形，且 ABCE （1）如图 1，连接 BG、DE求证：BGDE； （2）如图 2，如果正方形 CEFG 绕点 C 旋转到某一位置恰好使得 CGBD，BGBD 求BDE 的度数； 若正方形 ABCD 的边长是，请求出 BCG 的面积 （1）证明：四边形 ABCD 和四边形 CEFG 为正方形，

23、 BCDC，CGCE，BCDGCE90 BCD+DCGGCE+DCG， BCGDCE 在 BCG 和 DCE 中， BCGDCE（SAS） BGDE； （2）解：连接 BE，如图 2 所示： 由（1）可知：BGDE， CGBD， DCGBDC45 ， BCGBCD+DCG90 +45 135 ， GCE90 ， BCE360 BCGGCE360 135 90 135 ， BCGBCE， 在 BCG 和 BCE 中， BCGBCE（SAS）， BGBE， BGBDDE， BDBEDE， BDE 为等边三角形， BDE60 ； 延长 EC 交 BD 于点 H，过点 G 作 GNBC 于 N，如图

24、3 所示： 在 BCE 和 DCE 中， BCEBCG（SSS）， BECDEC， EHBD，BHBD， BCCD ， BDBC2， BE2，BH1， CH1， 在 Rt BHE 中，由勾股定理得：EH， CE1， BCG135 ， GCN45 ， GCN 是等腰直角三角形， GNCG（1）， S BCGBCGN（1） 15、利用“同角的余角相等”可以帮助我们得到相等的角，这个规律在全等三角形的判定中有着广泛的运用 （1）如图，B，C，D 三点共线，ABBD 于点 B，DEBD 于点 D，ACCE，且 ACCE 若 AB+DE6，求 BD 的长 （2）如图，在平面直角坐标系中， ABC 为等腰

25、直角三角形，直角顶点 C 的坐标为（1，0），点 A 的坐标为（2，1）求直线 AB 与 y 轴的交点坐标 （3）如图，ACB90 ，OC 平分AOB，若点 B 坐标为（b，0），点 A 坐标为（0，a）则 S四边形 AOBC （只需写出结果，用含 a，b 的式子表示） 解：（1）ABBD，DEBD，ACCE， ABCCDEACE90 ， A+ACB90 ，ECD+ACB180 ACE90 ， AECD， 在 ABC 和 CDE 中， ABCCDE（AAS）， ABCD，BCDE， BDCD+BCAB+DE6； （2）过点 A 作 ADx 轴于 D，过点 B 作 BEx 轴于 E，如图所示：

26、ABC 为等腰直角三角形 ADCCEBACB90 ，ACCB， DAC+ACD90 ，ECB+ACD180 ACB90 ， DACECB， 在 ADC 和 CEB 中， ADCCEB（AAS）， ADCE，CDBE， 点 C 的坐标为（1，0），点 A 的坐标为（2，1）， CO1，AD1，DO2， OEOC+CEOC+AD2，BECDCO+DO3， 点 B 的坐标为（2，3）， 设直线 AB 的解析式为 ykx+b， 将 A、B 两点的坐标代入，得， 解得：， 直线 AB 的解析式为：yx+2， 当 x0 时，解得 y2， 直线 AB 与 y 轴的交点坐标为（0，2）； （3）过点 C 作

27、CDy 轴于 D，CEx 轴于 E，如图所示： OC 平分AOB， CDCE 四边形 OECD 是正方形 DCE90 ，ODOE， ACB90 ， DCA+ACEECB+ACE90 ， DCAECB， 在 DCA 和 ECB 中， DCAECB（ASA）， DAEB，S DCAS ECB， 点 B 坐标为（b，0），点 A 坐标为（0，a）， OBb，OAa， ODOE， OA+DAOBBE， 即 a+DAbDA， DA ， ODOA+DAa+， S四边形AOBCS四边形AOEC+S ECBS四边形AOEC+S DCAS正方形DOECOD2（）2， 故答案为： 16、如图 1，将边长为 2 的

28、正方形 OABC 如图放置在直角坐标系中 （1）如图 2，若将正方形 OABC 绕点 O 顺时针旋转 30 时，求点 A 的坐标； （2）如图 3，若将正方形 OABC 绕点 O 顺时针旋转 75 时，求点 B 的坐标 解：（1）过点 A 作 ADx 轴于点 D，如图 2 所示： 则AOD30 ， 正方形 OABC 的边长为 2， AO2， ADAO1， OD ， 点 A 的坐标为：（，1）； （2）连接 OB，过点 B 作 BEx 轴于点 E，如图 3 所示： 则AOE75 ， 四边形 OABC 是正方形， AOB45 ，OBAO2， 在 Rt BOE 中，BOEAOEAOB30 ， BEOB，OE BE ， 点 B 的坐标为（，）