2021年高考数学(理)一轮复习题型归纳与训练 专题8.1 空间几何体的结构及其表面积、体积（教师版含解析）

《2021年高考数学(理)一轮复习题型归纳与训练 专题8.1 空间几何体的结构及其表面积、体积（教师版含解析）》由会员分享，可在线阅读，更多相关《2021年高考数学(理)一轮复习题型归纳与训练 专题8.1 空间几何体的结构及其表面积、体积（教师版含解析）（32页珍藏版）》请在七七文库上搜索。

1、2021 年高考理科数学一轮复习：题型全归纳与高效训练突破年高考理科数学一轮复习：题型全归纳与高效训练突破 专题专题 8.1 空间几何体的结构及其表面积、体积空间几何体的结构及其表面积、体积 目录 一、考点全归纳一、考点全归纳 1空间几何体的结构特征 (1)多面体的结构特征 多面体 结构特征 棱柱 有两个面互相平行，其余各面都是四边形且每相邻两个四边形的公 共边都互相平行 棱锥 有一个面是多边形，而其余各面都是有一个公共顶点的三角形 棱台 棱锥被平行于底面的平面所截，截面和底面之间的部分叫做棱台 (2)旋转体的形成 几何体 旋转图形 旋转轴 圆柱 矩形 矩形一边所在的直线 或对边中点连线所在直

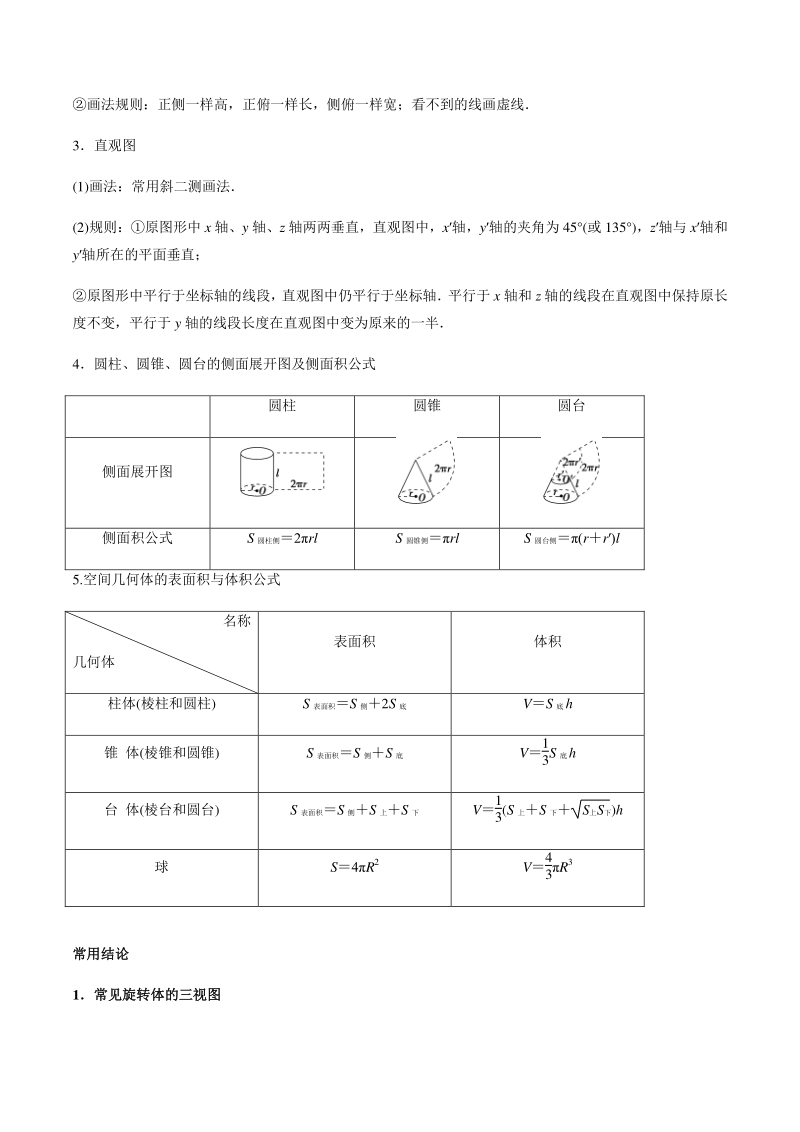
2、线 圆锥 直角三角形或等腰三角形 一直角边所在的直线或等腰 三角形底边上的高所在直线 圆台 直角梯形或等腰梯形 直角腰所在的直线或 等腰梯形上下底中点 连线所在直线 球 半圆或圆 直径所在的直线 2.三视图 (1)几何体的三视图包括正视图、侧视图、俯视图，分别是从几何体的正前方、正左方、正上方观察几何体 画出的轮廓线 (2)三视图的画法 基本要求：长对正，高平齐，宽相等 画法规则：正侧一样高，正俯一样长，侧俯一样宽；看不到的线画虚线 3直观图 (1)画法：常用斜二测画法 (2)规则：原图形中 x 轴、y 轴、z 轴两两垂直，直观图中，x轴，y轴的夹角为 45 (或 135 )，z轴与 x轴和

3、y轴所在的平面垂直； 原图形中平行于坐标轴的线段， 直观图中仍平行于坐标轴平行于 x 轴和 z 轴的线段在直观图中保持原长 度不变，平行于 y 轴的线段长度在直观图中变为原来的一半 4圆柱、圆锥、圆台的侧面展开图及侧面积公式 圆柱 圆锥 圆台 侧面展开图 侧面积公式 S圆柱侧2rl S圆锥侧rl S圆台侧(rr)l 5.空间几何体的表面积与体积公式 名称 几何体 表面积 体积 柱体(棱柱和圆柱) S表面积S侧2S底 VS底h 锥 体(棱锥和圆锥) S表面积S侧S底 V1 3S 底h 台 体(棱台和圆台) S表面积S侧S上S下 V1 3(S 上S下 S上S下)h 球 S4R2 V4 3R 3 常

4、用结论常用结论 1常见旋转体的三视图常见旋转体的三视图 (1)球的三视图都是半径相等的圆 (2)水平放置的圆锥的正视图和侧视图均为全等的等腰三角形 (3)水平放置的圆台的正视图和侧视图均为全等的等腰梯形 (4)水平放置的圆柱的正视图和侧视图均为全等的矩形 2斜二测画法中的斜二测画法中的“三变三变”与与“三不变三不变” “三变” 坐标轴的夹角改变 与y轴平行的线段的长度变为原来的一半 图形改变 “三不变” 平行性不改变 与x，z轴平行的线段的长度不改变 相对位置不改变 3正方体的外接球、内切球及与各条棱相切球的半径正方体的外接球、内切球及与各条棱相切球的半径 (1)外接球：球心是正方体的中心；半

5、径 r 3 2 a(a 为正方体的棱长) (2)内切球：球心是正方体的中心；半径 ra 2(a 为正方体的棱长) (3)与各条棱都相切的球：球心是正方体的中心；半径 r 2 2 a(a 为正方体的棱长). 4.正四面体的外接球、内切球的球心和半径正四面体的外接球、内切球的球心和半径 (1)正四面体的外接球与内切球(正四面体可以看作是正方体的一部分) (2)外接球：球心是正四面体的中心；半径 r 6 4 a(a 为正四面体的棱长) (3)内切球：球心是正四面体的中心；半径 r 6 12a(a 为正四面体的棱长) 二二 题型全归纳题型全归纳 题型一题型一 空间几何体的几何特征空间几何体的几何特征

6、【题型要点】解决与空间几何体结构特征有关问题的技巧【题型要点】解决与空间几何体结构特征有关问题的技巧 (1)关于空间几何体的结构特征辨析关键是紧扣各种空间几何体的概念， 要善于通过举反例对概念进行辨析， 即要说明一个命题是错误的，只需举一个反例即可 (2)圆柱、圆锥、圆台的有关元素都集中在轴截面上，解题时要注意用好轴截面中各元素的关系 (3)棱(圆)台是由棱(圆)锥截得的，所以在解决棱(圆)台问题时，要注意“还台为锥”的解题策略 【例【例 1】(2020 辽宁省鞍山一中高三上学期期末辽宁省鞍山一中高三上学期期末)给出下列命题： (1)棱柱的侧棱都相等，侧面都是全等的平行四边形； (2)若三棱锥

7、的三条侧棱两两垂直，则其三个侧面也两两垂直； (3)在四棱柱中，若两个过相对侧棱的截面都垂直于底面，则该四棱柱为直四棱柱； (4)存在每个面都是直角三角形的四面体； (5)棱台的侧棱延长后交于一点 其中正确命题的个数为( ) A2 B3 C4 D5 【答案】【答案】C 【解析】 (1)不正确， 根据棱柱的定义， 棱柱的各个侧面都是平行四边形， 但不一定全等； (2)正确，若三棱锥的三条侧棱两两垂直，则三个侧面构成的三个平面的二面角都是直二 面角； (3)正确， 因为两个过相对侧棱的截面的交线平行于侧棱， 又垂直于底面； (4)正确， 如图，正方体 ABCD- A1B1C1D1中的三棱锥 C1-

8、 ABC，四个面都是直角三角形；(5)正确， 由棱台的概念可知 【例例 2】给出下列几个命题： 在圆柱的上、下底面的圆周上各取一点，则这两点的连线是圆柱的母线； 底面为正多边形，且有相邻两个侧面与底面垂直的棱柱是正棱柱； 棱台的上、下底面可以不相似，但侧棱长一定相等 其中正确命题的个数是( ) A0 B1 C2 D3 【答案】B. 【解析】 ：不一定，只有这两点的连线平行于旋转轴时才是母线；正确；错误，棱台的上、下底面是 相似且对应边平行的多边形，各侧棱延长线交于一点，但是侧棱长不一定相等 题型二题型二 空间几何体的三视图空间几何体的三视图 【题型要点】三视图问题的常见类型及解题策略【题型要点

9、】三视图问题的常见类型及解题策略 (1)由几何体的直观图求三视图注意正视图、侧视图和俯视图的观察方向，注意看到的部分用实线表示， 看不到的部分用虚线表示 (2)由几何体的部分视图画出剩余的视图先根据已知的一部分视图，还原、推测其直观图的可能形式，然 后再找其剩下部分视图的可能形式当然作为选择题，也可将选项逐项代入，再看看给出的部分三视图是 否符合 (3)由几何体的三视图还原几何体的形状要熟悉柱、锥、台、球的三视图，明确三视图的形成原理，结合 空间想象将三视图还原为直观图 类型一类型一 已知几何体，识别三视图已知几何体，识别三视图 【例【例 1】(2020 宜宾模拟宜宾模拟)已知棱长都为 2 的

10、正三棱柱 ABC- A1B1C1的直观图如图若正三棱柱 ABC- A1B1C1 绕着它的一条侧棱所在直线旋转，则它的侧视图可以为( ) 【答案】B 【解析】 由题知， 四个选项的高都是 2.若侧视图为 A， 则中间应该有一条竖直的实线或虚线； 若侧视图为 C， 则其中有两条侧棱重合，不应有中间竖线；若侧视图为 D，则长度应为 3，而不是 1.故选 B. 【例【例 2】 (2020 湖南衡阳二模湖南衡阳二模)如图， 正方体ABCD- A1B1C1D1的顶点 A， B 在平面 上， AB 2.若平面 A1B1C1D1 与平面 所成角为 30 ， 由如图所示的俯视方向， 正方体 ABCD- A1B1

11、C1D1在平面 上的俯视图的面积为( ) A2 B1 3 C2 3 D2 2 【答案】B 【解析】 由题意得 AB 在平面 内， 且平面 与平面 ABCD 所成的角为 30 ， 与平面 B1A1AB 所成的角为 60 ， 故所得的俯视图的面积 S 2 ( 2cos 30 2cos 60 )2(cos 30 cos 60 )1 3. 类型二类型二 已知三视图，判断几何体已知三视图，判断几何体 【例【例 3】如图，网格纸的各小格都是正方形，粗实线画出的是一个几何体的三视图，则这个几何体是( ) A三棱锥 B三棱柱 C四棱锥 D四棱柱 【答案】B 【解析】由题三视图得直观图如图所示 为三棱柱，故选

12、B. 【例【例 4】某四棱锥的三视图如图所示，在此四棱锥的侧面中，直角三角形的个数为( ) A1 B2 C3 D4 【答案】C 【解析】将三视图还原为直观图，几何体是底面为直角梯形，且一条侧棱和底面垂直的四棱锥，如图所示 易知，BCAD，BC1，ADABPA2， ABAD，PA平面 ABCD，故 PAD， PAB 为直角三角形， 因为 PA平面 ABCD， BC平面 ABCD， 所以 PABC，又 BCAB，且 PAABA， 所以 BC平面 PAB，又 PB平面 PAB，所以 BCPB， 所以 PBC 为直角三角形，容易求得 PC3，CD 5，PD2 2， 故 PCD 不是直角三角形，故选 C

13、. 类型三类型三 已知几何体的某些视图，判断其他视图已知几何体的某些视图，判断其他视图 【例【例 5】(2020 福州模拟福州模拟)如图为一圆柱切削后的几何体及其正视图，则相应的侧视图可以是( ) 【答案】B 【解析】圆柱被不平行于底面的平面所截，得到的截面为椭圆，结合正视图，可知侧视图最高点在中间， 故选 B. 【例【例 6】(2020 河北衡水中学联考河北衡水中学联考)九章算术是我国古代内容极为丰富的数学名著，书中有如下问题：“今 有刍甍，下广三丈，袤四丈，上袤二丈，无广，高二丈，问：积几何？”其意思为：“今有底面为矩形的屋脊 状的楔体，下底面宽 3 丈、长 4 丈，上棱长 2 丈，高 2

14、 丈，问：它的体积是多少？”已知该楔体的正视图和 俯视图如图中粗实线所示，则该楔体的侧视图的周长为( ) A3 丈 B6 丈 C8 丈 D(5 13)丈 【答案】C 【解析】由题意可知该楔体的侧视图是等腰三角形，它的底边长为 3 丈，相应高为 2 丈，所以腰长为 22 3 2 2 5 2(丈)，所以该楔体侧视图的周长为 32 5 28(丈)故选 C. 题型三题型三 空间几何体的直观图空间几何体的直观图 【题型要点】【题型要点】(1)斜二测画法中的斜二测画法中的“三变三变”与与“三不变三不变” “三变” 坐标轴的夹角改变 与y轴平行的线段的长度变为原来的一半 图形改变 “三不变” 平行性不改变

15、与x，z轴平行的线段的长度不改变 相对位置不改变 (2)平面图形直观图与原图形面积间的关系平面图形直观图与原图形面积间的关系 对于几何体的直观图，除掌握斜二测画法外，记住原图形面积 S 与直观图面积 S之间的关系 S 2 4 S，能更 快捷地进行相关问题的计算 【例【例 1】已知等边三角形 ABC 的边长为 a，那么 ABC 的平面直观图 ABC的面积为( ) A. 3 4 a2 B 3 8 a2 C. 6 8 a2 D 6 16a 2 【答案】D. 【解析】 ：如图所示的实际图形和直观图， 由可知， ABABa， OC1 2OC 3 4 a， 在图中作CDAB于点D， 则CD 2 2 OC

16、6 8 a.所以S ABC 1 2ABCD 1 2 a 6 8 a 6 16a 2.故选 D. 【例【例 2】 】 在等腰梯形 ABCD 中，上底 CD1，腰 ADCB 2，下底 AB3，以下底所在直线为 x 轴，则 由斜二测画法画出的直观图 ABCD的面积为_ 【答案】 ： 2 2 【解析】 ：因为 OE（ 2）2121， 所以 OE1 2，EF 2 4 . 所以直观图 ABCD的面积为 S1 2 (13) 2 4 2 2 . 题型四题型四 空间几何体的表面积空间几何体的表面积 【题型要点】几类空间几何体表面积的求法【题型要点】几类空间几何体表面积的求法 (1)多面体：其表面积是各个面的面积

17、之和 (2)旋转体：其表面积等于侧面面积与底面面积的和 (3)简单组合体：应搞清各构成部分，并注意重合部分的删、补 (4)若以三视图形式给出，解题的关键是根据三视图，想象出原几何体及几何体中各元素间的位置关系及数 量关系 【例【例 1】(2020 河南周口模拟河南周口模拟)如图，在三棱柱 ABC- A1B1C1中，AA1底面 ABC，ABBC，AA1AC2，直 线 A1C 与侧面 AA1B1B 所成的角为 30 ，则该三棱柱的侧面积为( ) A44 2 B44 3 C12 D84 2 【答案】A 【解析】 连接 A1B.因为 AA1底面 ABC，则 AA1BC，又 ABBC，AA1ABA，所以

18、 BC平面 AA1B1B，所以直线 A1C 与侧面 AA1B1B 所成的角为CA1B30 .又 AA1AC2，所以 A1C2 2，BC 2.又 ABBC，则 AB 2，则该三棱柱的侧面积为 2 2 22 244 2，故选 A. 【例【例 2】(2020 四川泸州一诊四川泸州一诊)在梯形 ABCD 中，ABC 2，ADBC，BC2AD2AB2.将梯形 ABCD 绕 AD 所在的直线旋转一周而形成的曲面所围成的几何体的表面积为( ) A(5 2) B(4 2) C(52 2) D(3 2) 【答案】A 【解析】 因为在梯形 ABCD 中，ABC 2，ADBC，BC2AD2AB2，所以将梯形 ABC

19、D 绕 AD 所在的直线旋 转一周而形成的曲面所围成的几何体是一个底面半径为 AB1，高为 BCAD211 的圆锥，所以该几 何体的表面积 S122121 1212(5 2).故选 A. 题型五题型五 空间几何体的体积空间几何体的体积 【题型要点】处理体积问题的思路【题型要点】处理体积问题的思路 “转转”：指的是转换底面与高，将原来不易求面积的底面转换为易求面积的底面，或将原来不易看出的高 转换为易看出并易求解长度的高； “拆拆”：指的是将一个不规则的几何体拆成几个简单的几何体，便于计算； “拼拼”：指的是将小几何体嵌入一个大几何体中，如将一个三棱锥复原成一个三棱柱，将一个三棱柱复原 成一个四

20、棱柱，这些都是拼补的方法 (2)求空间几何体的体积的常用方法求空间几何体的体积的常用方法 公式法：公式法：对于规则几何体的体积问题，可以直接利用公式进行求解； 割补法：割补法：把不规则的图形分割成规则的图形，然后进行体积计算；或者把不规则的几何体补成规则的几 何体，不熟悉的几何体补成熟悉的几何体，便于计算其体积； 等体积法：等体积法：一个几何体无论怎样转化， 其体积总是不变的 如果一个几何体的底面面积和高较难求解时， 我们可以采用等体积法进行求解等体积法也称等积转化或等积变形，它是通过选择合适的底面来求几何 体体积的一种方法，多用来解决有关锥体的体积，特别是三棱锥的体积 类型一类型一 直接利用

21、公式求体积直接利用公式求体积 【例【例 1】(2020 山东省实验中学模拟山东省实验中学模拟)我国古代九章算术里，记载了一个“商功”的例子：今有刍童，下广 二丈，袤三丈，上广三丈，袤四丈，高三丈问积几何？其意思是：今有上下底面皆为长方形的草垛(如图 所示)，下底宽 2 丈，长 3 丈，上底宽 3 丈，长 4 丈，高 3 丈问它的体积是多少？该书提供的算法是：上 底长的 2 倍与下底长的和与上底宽相乘，同样下底长的 2 倍与上底长的和与下底宽相乘，将两次运算结果 相加，再乘以高，最后除以 6.则这个问题中的刍童的体积为( ) A13.25 立方丈 B26.5 立方丈 C53 立方丈 D106 立

22、方丈 【答案】B 【解析】由题意知，刍童的体积为(4 23) 3(3 24) 2 3 626.5(立方丈)，故选 B. 类型二类型二 割补法求体积割补法求体积 【例【例 2】 九章算术卷五商功中有如下问题：今有刍甍，下广三丈，袤四丈，上袤二丈，无广，高一丈， 问积几何？刍甍：底面为矩形的屋脊状的几何体(网格纸中粗线部分为其三视图，设网格纸上每个小正方形 的边长为 1)，那么该刍甍的体积为( ) A4 B5 C6 D12 【答案】B 【解析】如图所示， 由三视图可还原得到几何体 ABCDEF，过 E，F 分别作垂直于底面的截面 EGH 和 FMN，可将原几何体切割 成三棱柱 EHG- FNM，四

23、棱锥 E- ADHG 和四棱锥 F- MBCN，易知三棱柱的体积为1 2 3 1 23，两个四棱锥 的体积相同，都为1 3 1 3 11，则原几何体的体积为 3115.故选 B. 类型三类型三 等体积法求体积等体积法求体积 【例【例 3】(2020 贵州部分重点中学联考贵州部分重点中学联考)如图，在直四棱柱 ABCD- A1B1C1D1中，底面 ABCD 是平行四边形， 点 E 是棱 BB1的中点，点 F 是棱 CC1上靠近 C1的三等分点，且三棱锥 A1- AEF 的体积为 2，则四棱柱 ABCD- A1B1C1D1的体积为( ) A12 B8 C20 D18 【答案】A 【解析】 设点 F

24、 到平面 ABB1A1的距离为 h， 由题意得 VA1- AEFVF- A1AE.又 VF- A1AE1 3S A1AE h 1 3 1 2AA1 AB h 1 6(AA1 AB) h 1 6S 四边形 ABB1A1 h 1 6VABCD- A1B1C1D1，所以 VABCD- A1B1C1D16VA1- AEF6 212.所以四棱柱 ABCD- A1B1C1D1的体积为 12.故选 A. 题型六题型六 球与空间几何体的接、切问题球与空间几何体的接、切问题 【题型要点】与球有关的切、接问题的解法【题型要点】与球有关的切、接问题的解法 (1)旋转体的外接球：常用的解题方法是过球心及接、切点作截面

25、，把空间问题转化为平面图形与圆的接、 切问题，再利用平面几何知识寻找几何中元素间的关系求解 (2)多面体的外接球：常用的解题方法是将多面体还原到正方体和长方体中再去求解 若球面上四点 P，A，B，C 中 PA，PB，PC 两两垂直或三棱锥的三条侧棱两两垂直，可构造长方体或正 方体，利用 2R a2b2c2求 R. 一条侧棱垂直底面的三棱锥问题：可补形成直三棱柱先借助几何体的几何特征确定球心位置，然后把 半径放在直角三角形中求解 (3)解题流程 类型一类型一 外接球外接球 【例【例 1】 已知圆柱的高为 1， 它的两个底面的圆周在直径为 2 的同一个球的球面上， 则该圆柱的体积为( ) A B3

26、 4 C. 2 D 4 【答案】B 【解析】设圆柱的底面圆半径为 r，则 r212 1 2 2 3 4，所以，圆柱的体积 V 3 41 3 4 ，故选 B. 【例【例 2】已知三棱锥 S- ABC 的所有顶点都在球 O 的球面上，SC 是球 O 的直径若平面 SCA平面 SCB，SA AC，SBBC，三棱锥 S- ABC 的体积为 9，则球 O 的表面积为_ 【答案】36 【解析】【解析】设球 O 的半径为 R，因为 SC 为球 O 的直径，所以点 O 为 SC 的中点，连接 AO，OB，因为 SA AC，SBBC，所以 AOSC，BOSC，因为平面 SCA平面 SCB，平面 SCA平面 SC

27、BSC，所以 AO 平面 SCB，所以 VS- ABCVA- SBC1 3 S SBC AO 1 3 ( 1 2 SC OB) AO，即 9 1 3 ( 1 2 2R R) R，解得 R3，所以 球 O 的表面积为 S4R243236. 类型二类型二 内切球内切球 【例【例 3】如图，在圆柱 O1O2内有一个球 O，该球与圆柱的上、下底面及母线均相切记圆柱 O1O2的体积为 V1，表面积为 S1，球 O 的体积为 V2，表面积为 S2，则V1 V2的值是_， S1 S2_. 【答案】3 2 3 2 【解析】 设圆柱内切球的半径为 R， 则由题设可得圆柱 O1O2的底面圆的半径为 R， 高为 2

28、R， 所以V1 V2 R2 2R 4 3R 3 3 2. S1 S2 2R 2R2R2 4R2 3 2. 【例【例 4】已知棱长为 a 的正四面体，则此正四面体的表面积 S1与其内切球的表面积 S2的比值为_ 【答案】6 3 【解析】 正四面体的表面积为 S14 3 4 a2 3a2， 其内切球半径 r 为正四面体高的1 4， 即 r 1 4 6 3 a 6 12a， 因此内切球表面积为 S24r2a 2 6 ，则S1 S2 3a2 a2 6 6 3 . 类型三类型三 确定球心位置的三种方法确定球心位置的三种方法 决定球的几何要素是球心的位置和球的半径，在球与其他几何体的结合问题中，通过位置关

29、系的分析，找 出球心所在的位置是解题的关键，不妨称这个方法为球心位置分析法 方法一方法一 由球的定义确定球心由球的定义确定球心 若一个多面体的各顶点都在一个球的球面上，则称这个多面体是这个球的内接多面体，这个球是这个多面 体的外接球也就是说如果一个定点到一个简单多面体的所有顶点的距离都相等，那么这个定点就是该简 单多面体外接球的球心 (1)长方体或正方体的外接球的球心是其体对角线的中点； (2)正三棱柱的外接球的球心是上、下底面中心连线的中点； (3)直三棱柱的外接球的球心是上、下底面三角形外心连线的中点； (4)正棱锥的外接球球心在其高上，具体位置可通过建立直角三角形运用勾股定理计算得到；

30、(5)若棱锥的顶点可构成共斜边的直角三角形，则公共斜边的中点就是其外接球的球心 【例【例 1】已知各顶点都在同一个球面上的正四棱柱的高为 4，体积为 16，则这个球的表面积是( ) A16 B20 C24 D32 【答案】C 【解析】已知各顶点都在同一个球面上的正四棱柱的高为 4，体积为 16，可求得底面边长为 2，故球的直径 为 2222422 6，则半径为 6，故球的表面积为 24，故选 C. 方法二方法二 构造长方体或正方体确定球心构造长方体或正方体确定球心 (1)正四面体、三条侧棱两两垂直的正三棱锥、四个面都是直角三角形的三棱锥，可将三棱锥补形成长方体 或正方体； (2)同一个顶点上的

31、三条棱两两垂直的四面体、 相对的棱相等的三棱锥， 可将三棱锥补形成长方体或正方体； (3)若已知棱锥含有线面垂直关系，则可将棱锥补形成长方体或正方体； (4)若三棱锥的三个侧面两两垂直，则可将三棱锥补形成长方体或正方体 【例【例 2】如图，边长为 2 的正方形 ABCD 中，点 E，F 分别是边 AB，BC 的中点，将 AED， EBF， FCD 分别沿 DE，EF，FD 折起，使 A，B，C 三点重合于点 A，若四面体 AEFD 的四个顶点在同一个球面上， 则该球的半径为( ) A. 2 B 6 2 C. 11 2 D 5 2 【答案】B 【解析】易知四面体 AEFD 的三条侧棱 AE，AF

32、，AD 两两垂直，且 AE1，AF1，AD2，把四面体 AEFD 补成从顶点 A出发的三条棱长分别为 1，1，2 的一个长方体，则长方体的外接球即为四面体 AEFD 的外接球，球的半径为 r1 2 121222 6 2 .故选 B. 方法三方法三 由性质确定球心由性质确定球心 利用球心 O 与截面圆圆心 O的连线垂直于截面圆及球心 O 与弦中点的连线垂直于弦的性质，确定球心 【例【例 3】正三棱锥 A- BCD 内接于球 O，且底面边长为 3，侧棱长为 2，则球 O 的表面积为_ 【答案】16 3 【解析】 如图 M 为底面 BCD 的中心，易知 AMMD，DM1，AM 3.在 Rt DOM

33、中，OD2OM2MD2，即 OD2 ( 3OD)21，解得 OD2 3 3 ，故球 O 的表面积为 4 2 3 3 2 16 3 . 二、高效训练突破二、高效训练突破 一、选择题一、选择题 1中国古建筑借助榫卯将木构件连接起来构件的凸出部分叫榫头，凹进部分叫卯眼，图中木构件右边的 小长方体是榫头若如图摆放的木构件与某一带卯眼的木构件咬合成长方体，则咬合时带卯眼的木构件的 俯视图可以是( ) 【答案】A. 【解析】 ：由题意知，在咬合时带卯眼的木构件中，从俯视方向看，榫头看不见，所以是虚线，结合榫头的 位置知选 A. 2 (2020 安徽宣城二模安徽宣城二模)一个几何体的三视图如图所示， 在该几

34、何体的各个面中， 面积最大面的面积是( ) A2 B2 2 C2 3 D4 【答案】C. 【解析】 ：如图所示 由三视图可知该几何体是四棱锥 P- ABCD 截去三棱锥 P- ABD 后得到的三棱锥 P- BCD.其中四棱锥中，底面 ABCD 是正方形，PA底面 ABCD，且 PAAB2，易知面积最大面为面 PBD，面积为 3 4 (2 2)22 3.故 选 C. 3某圆柱的高为 2，底面周长为 16，其三视图如图圆柱表面上的点 M 在正视图上的对应点为 A，圆柱表 面上的点 N 在左视图上的对应点为 B，则在此圆柱侧面上，从 M 到 N 的路径中，最短路径的长度为( ) A2 17 B2 5

35、 C3 D2 【答案】B. 【解析】 ：由三视图可知，该几何体为如图所示的圆柱，该圆柱的高为 2，底面周长为 16.画出该圆柱的侧 面展开图， 如图所示， 连接 MN， 则 MS2， SN4， 则从 M 到 N 的路径中， 最短路径的长度为 MS2SN2 22422 5.故选 B. 4.一个几何体的三视图如图所示，图中直角三角形的直角边长均为 1，则该几何体的体积为( ) A.1 6 B 2 6 C. 3 6 D1 2 【答案】A 【解析】 几何体还原说明：画出正方体，俯视图中实线可以看作正方体的上底面及底面对角线俯视图是正方 形， 有四个直角， 正视图和侧视图中分别有一个直角 正视图和侧视图

36、中的直角对应上底面左边外侧顶点(图 中 D 点上方顶点)，将该顶点下拉至 D 点，连接 DA，DB，DC 即可该几何体即图中棱长为 1 的正方体中 的四面体 ABCD，其体积为1 3 1 2 1 1 1 1 6.故选 A. 5(2020 陕西彬州质检陕西彬州质检)一个几何体的三视图如图所示，其中正视图中 ABC 是边长为 1 的等边三角形，俯 视图为正六边形，那么该几何体的侧视图的面积为( ) A.3 8 B 3 4 C1 D 3 2 【答案】A. 【解析】 ：由三视图可知该几何体为正六棱锥，其直观图如图所示 该正六棱锥的底面正六边形的边长为1 2，侧棱长为 1，高为 3 2 .侧视图的底面边

37、长为正六边形的高，为 3 2 ， 则该几何体的侧视图的面积为1 2 3 2 3 2 3 8，故选 A. 6(2020 江西省名校学术联盟质检江西省名校学术联盟质检)如图所示，边长为 1 的正方形网格中粗线画出的是某几何体的三视图， 则该几何体所有棱长组成的集合为( ) A1， 5 B1， 6 C1， 2， 5 D1， 2，2 2， 6 【答案】B. 【解析】 ：如图所示 该几何体是四棱柱，底面是边长为 1 的正方形，侧棱长为 6，故选 B. 7 (2020 河南非凡联盟河南非凡联盟 4 月联考月联考)某组合体的正视图和侧视图如图(1)所示， 它的俯视图的直观图是图(2)中粗 线所表示的平面图形

38、，其中四边形 OABC为平行四边形，D为 CB的中点，则图(2)中平行四边形 OABC 的面积为( ) A12 B3 2 C6 2 D6 【答案】B. 【解析】 ：法一：由题图易知，该几何体为一个四棱锥(高为 2 3，底面是长为 4，宽为 3 的矩形)与一个半圆 柱(底面圆半径为 2，高为 3)的组合体，所以其俯视图的外侧边沿线组成一个长为 4，宽为 3 的矩形，其面积 为 12，由斜二测知识可知四边形 OABC的面积为 4 3 2sin 45 3 2. 法二：由斜二测画法可先还原出俯视图的外轮廓是长为 4，宽为 3 的矩形，其面积为 4 312，结合直观图 面积是原图形面积的 2 4 ，即可

39、得结果 8(2020 安徽黄山一模安徽黄山一模)如图所示为某几何体的三视图，则几何体的体积为( ) A.1 2 B1 C.3 2 D3 【答案】B. 【解析】 ： 由三视图可得如图的四棱锥 P- ABCD， 其中平面 ABCD平面 PCD.由正视图和俯视图可知 AD1， CD2， P 到平面 ABCD 的距离为3 2.所以四棱锥 P- ABCD 的体积为 V 1 3 S 长方形ABCD h1 3 1 2 3 21.故选 B. 9(2020 湖南永州三模湖南永州三模)某几何体的三视图如图所示，则该几何体的体积为( ) A.5 3 B4 3 C. 3 D2 3 【答案】D. 【解析】 ：几何体是半

40、个圆柱挖去半个圆锥所形成的，如图， 由题意可知几何体的体积为：1 2 1 221 3 1 2 1 222 3 .故选 D. 10(2020 广东茂名一模广东茂名一模)在长方体 ABCD- A1B1C1D1中，四边形 ABCD 是边长为 2 的正方形，D1B 与 DC 所 成的角是 60 ，则长方体的外接球的表面积是( ) A16 B8 C4 D4 2 【答案】A. 【解析】 ：如图，在长方体 ABCD- A1B1C1D1中，因为 DCAB，所以相交直线 D1B 与 AB 所成的角是异面直 线 D1B 与 DC 所成的角 连接 AD1，由 AB平面 ADD1A1，得 ABAD1，所以在 Rt A

41、BD1中，ABD1就是 D1B 与 DC 所成的角， 即ABD160 ，又 AB2，ABBD1cos 60 ， 所以 BD1 AB cos 60 4，设长方体 ABCD- A1B1C1D1外接球的半径为 R，则由长方体的体对角线就是长方体外 接球的直径得 4R2D1B216，则 R2，所以长方体外接球的表面积是 4R216.故选 A. 11(2020 江西萍乡一模江西萍乡一模)如图，网格纸上小正方形的边长为 1，粗线画的是某几何体的三视图，则该几何体 的体积为( ) A.23 6 B7 2 C. 7 6 D4 【答案】A. 【解析】 ：由三视图可得，该几何体是如图所示的三棱柱 ABB1- DC

42、C1， 挖去一个三棱锥 E- FCG 所形成的，故所求几何体的体积为 1 2 (2 2) 2 1 3 1 2 1 1 1 23 6 .故选 A. 12(2020 福建厦门外国语学校模拟福建厦门外国语学校模拟)已知等腰直角三角形 ABC 中，ACB90 ，斜边 AB2，点 D 是斜边 AB 上一点(不同于点 A， B) 沿线段 CD 折起形成一个三棱锥 A- CDB， 则三棱锥 A- CDB 体积的最大值是( ) A1 B1 2 C. 1 3 D 1 6 【答案】D. 【解析】 ： 设 ADx， 将 ACD 折起使得平面 ACD平面 BCD.在 ACD 中， 由面积公式得1 2CD h1 1 2

43、AD 1(h1 为点 A 到直线 CD 的距离)， 则 h1 x 1（x1）2.由题易知 h 1为点 A 到平面 BCD 的距离， 故三棱锥 A- CDB 体积为 V1 3S BCD h1 1 3 1 2BD 1 h1 1 6 2xx2 x22x2，x(0，2)令 t x 22x2，则 t1， 2)，故 V 1 6 2t2 t 1 6 2 tt .由于 2 tt 是减函数，故当 t1 时，V 取得最大值为 1 6 (21) 1 6.故选 D. 二、填空题二、填空题 1一个圆台上、下底面的半径分别为 3 cm 和 8 cm，若两底面圆心的连线长为 12 cm，则这个圆台的母线长 为_cm. 【答

44、案】 ：13 【解析】 ：如图 过点 A 作 ACOB，交 OB 于点 C. 在 Rt ABC 中，AC12(cm)，BC835(cm) 所以 AB 1225213(cm) 2已知正四棱锥 V- ABCD 中，底面面积为 16，一条侧棱的长为 2 11，则该棱锥的高为_ 【答案】 ：6 【解析】 ：如图 取正方形 ABCD 的中心 O，连接 VO，AO，则 VO 就是正四棱锥 V- ABCD 的高因为底面面积为 16，所以 AO2 2.因为一条侧棱长为 2 11，所以 VO VA2- AO2 4486.所以正四棱锥 V- ABCD 的高为 6. 3某几何体的正视图和侧视图如图(1)，它的俯视图

45、的直观图是矩形 O1A1B1C1，如图(2)，其中 O1A16， O1C12，则该几何体的侧面积为_ 【答案】 ：96 【解析】 ：由题图(2)及斜二测画法可知原俯视图为如图所示的平行四边形 OABC， 设 CB 与 y 轴的交点为 D，则易知 CD2，OD2 2 24 2，所以 CO CD2OD26OA，所以俯视 图是以 6 为边长的菱形，由三视图知几何体为一个直四棱柱，其高为 4，所以该几何体的侧面积为 4 6 4 96. 4(2019 高考全国卷高考全国卷)中国有悠久的金石文化，印信是金石文化的代表之一，印信的形状多为长方体、正 方体或圆柱体，但南北朝时期的官员独孤信的印信形状是“半正多

46、面体”(图 1)半正多面体是由两种或两种 以上的正多边形围成的多面体半正多面体体现了数学的对称美图 2 是一个棱数为 48 的半正多面体，它 的所有顶点都在同一个正方体的表面上，且此正方体的棱长为 1，则该半正多面体共有_个面，其棱 长为_ 【答案】 ：26 21 【解析】 ：依题意知，题中的半正多面体的上、下、左、右、前、后 6 个面都在正方体的表面上，且该半正 多面体的表面由 18 个正方形，8 个正三角形组成，因此题中的半正多面体共有 26 个面注意到该半正多面 体的俯视图的轮廓是一个正八边形， 设题中的半正多面体的棱长为 x， 则 2 2 xx 2 2 x1， 解得 x 21， 故题中

47、的半正多面体的棱长为 21. 5.已知圆锥 SO，过 SO 的中点 P 作平行于圆锥底面的截面，以截面为上底面作圆柱 PO，圆柱的下底面落在 圆锥的底面上(如图)，则圆柱 PO 的体积与圆锥 SO 的体积的比值为_ 【答案】 ：3 8 【解析】 ：设圆锥 SO 的底面半径为 r，高为 h，则圆柱 PO 的底面半径是r 2，高为 h 2，所以 V 圆锥SO1 3r 2h，V 圆柱PO r 2 2 h 2 r2h 8 ，所以V 圆柱PO V圆锥SO 3 8. 6 已知正三棱锥的高为 1， 底面边长为 2 3， 内有一个球与四个面都相切， 则棱锥的内切球的半径为_ 【答案】 ： 21 【解析】 ：如图 过点 P 作 PD平面 ABC 于点 D，连接 AD 并延长交 BC