初二数学讲义直升班 第7讲 正方形（教师版）

《初二数学讲义直升班 第7讲 正方形（教师版）》由会员分享，可在线阅读，更多相关《初二数学讲义直升班 第7讲 正方形（教师版）（10页珍藏版）》请在七七文库上搜索。

1、正正方形方形 模块一 正方形的性质和判定 模块二 弦图 模块三 垂直且相等模型 模块一模块一 正方形的性质和判定正方形的性质和判定 1定义：定义：四个角相等、四条边也相等的四边形叫作正方形 2性质：性质：正方形既是矩形，又是菱形，具有矩形和菱形的一切性质 性质 1：正方形的四个内角都相等，且都为，四条边都相等 性质 2：正方形的对角线互相垂直平分且相等，对角线平分一组对角 性质 3：正方形具有 4 条对称轴，两条对角线所在的直线和过两组对边中点的两条直线 另外，由正方形的性质可以得出： （1）正方形的对角线把正方形分成四个小的等腰直角三角形 （2）正方形的面积是边长的平方，也可表示为对角线长平

2、方的一半 3判定：判定：判定一个四边形是正方形，除了定义之外，还可以采用以下方法： （1）先证明是矩形，再证明该矩形有一组邻边相等，或对角线互相垂直 （2）先证明是菱形，再证明该菱形的一个角是直角，或两条对角线相等 模块二模块二 弦图及相关模型弦图及相关模型 1内弦图内弦图 2外弦图外弦图 （1）关于两个弦图的做法： 内弦图： 在正方形 ABCD 的各边上分别取 E、 F、 G、 H 四个点， 使得AEDHCGBF， 连接 EH、 HG、 GF、FE 可以得到内弦图 外弦图：在正方形 ABCD 内，分别取点 E、F、G、H 四个点，连接 AH、BE、CF、DG，使得 DAHCDGBCFABE

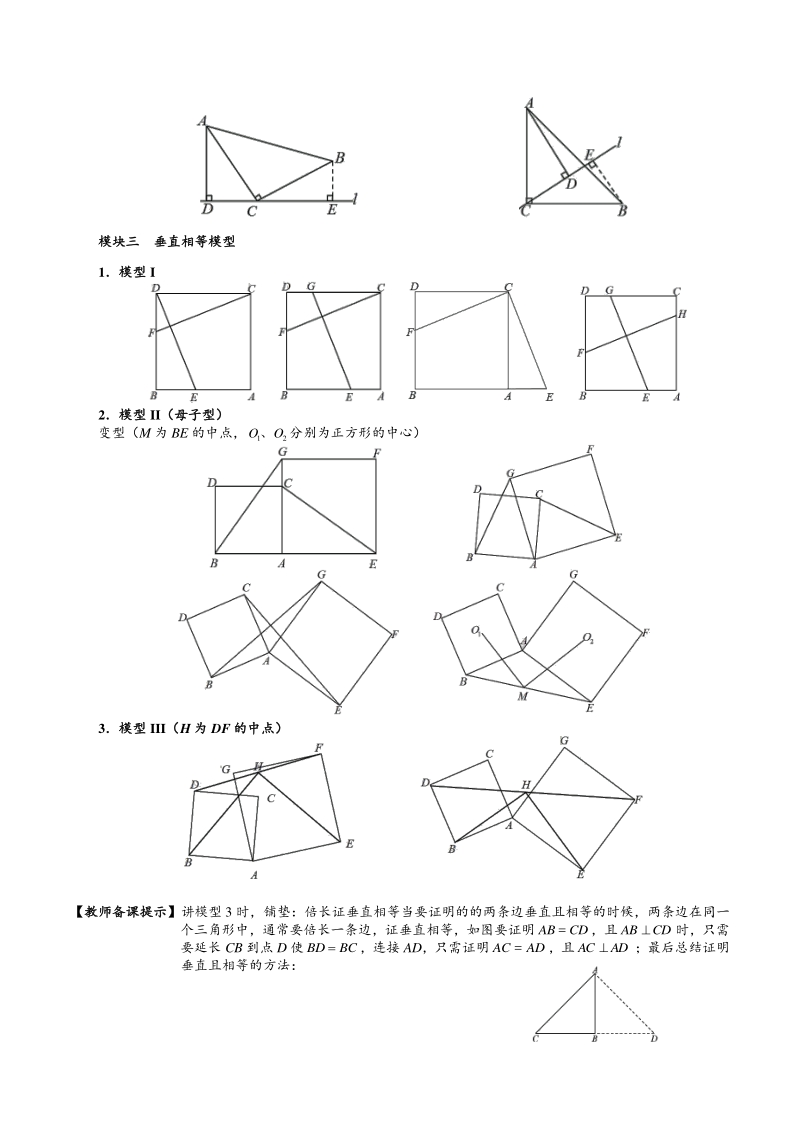
3、，就可以得到外弦图 （2）关于弦图的作用： 由弦图的做法，我们知道会产生四个全等的直角三角形，所以我们在平时的测试中会遇到这两个弦图或者 其中的一部分，我们会常利用这两个弦图去构造全等去解决一些难题。具体应用：证明勾股定理；解决复 杂的面积问题；构造全等三角形，求边的关系 （3）弦图常见辅助线添加方法： （ABC是等腰直角三角形） 模块三模块三 垂直相等模型垂直相等模型 1模型模型 I 2模型模型 II（母子型）（母子型） 变型（M 为 BE 的中点，OO 、分别为正方形的中心） 3模型模型 III（H 为为 DF 的中点）的中点） 【教师备课提示】【教师备课提示】讲模型 3 时，铺垫：倍长证

4、垂直相等当要证明的的两条边垂直且相等的时候，两条边在同一 个三角形中，通常要倍长一条边，证垂直相等，如图要证明=ABCD，且ABCD时，只需 要延长 CB 到点 D 使BDBC，连接 AD，只需证明=ACAD，且ACAD；最后总结证明 垂直且相等的方法： 1构造全等构造全等 当要证明的的两条边垂直且相等的时候，两条边没有在同一个三角形中，通常要构造两个边 所在的三角形全等 2倍长证垂直相等倍长证垂直相等 当要证明的的两条边垂直且相等的时候，两条边在同一个三角形中，通常要倍长一条边，证 垂直相等，如图要证明=ABCD，且ABCD时，只需要延长 CB 到点 D 使BDBC，连接 AD，只需证明=A

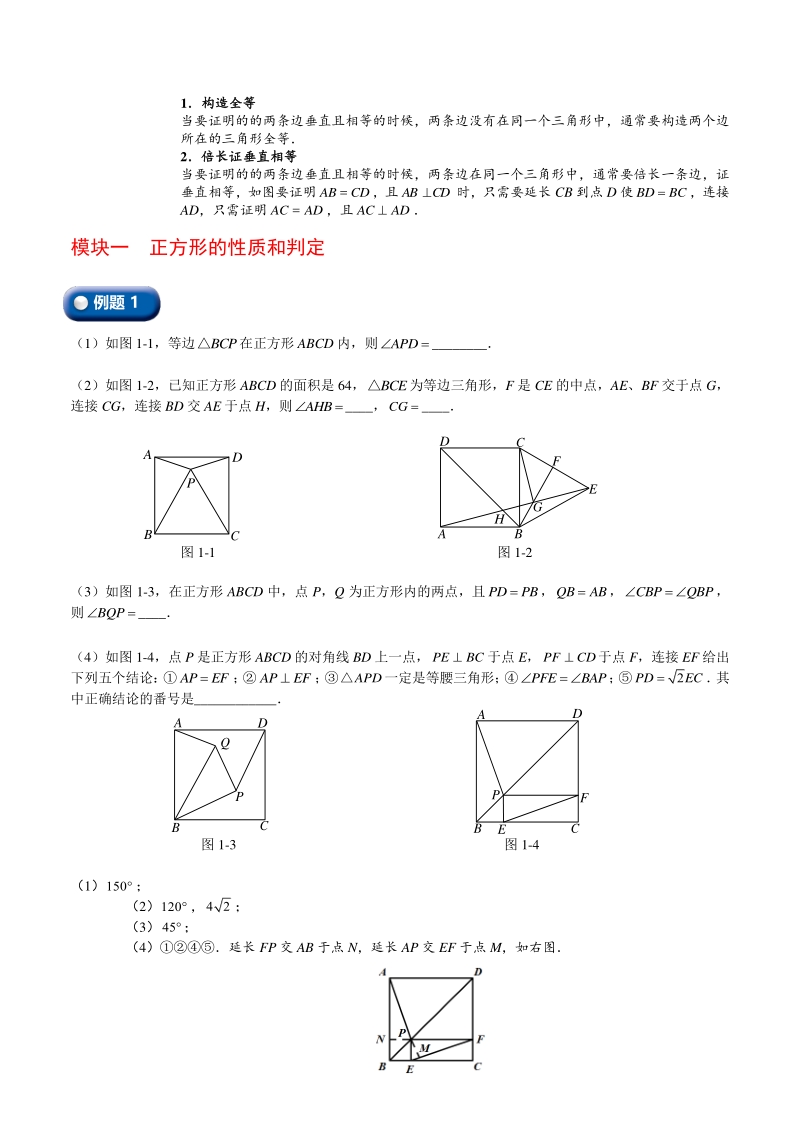
5、CAD，且ACAD 模块一 正方形的性质和判定 （1）如图 1-1，等边BCP在正方形 ABCD 内，则APD_ （2）如图 1-2，已知正方形 ABCD 的面积是 64，BCE为等边三角形，F 是 CE 的中点，AE、BF 交于点 G， 连接 CG，连接 BD 交 AE 于点 H，则AHB_，CG _ 图 1-1 图 1-2 （3）如图 1-3，在正方形 ABCD 中，点 P，Q 为正方形内的两点，且PDPB，QBAB，CBPQBP， 则BQP_ （4）如图 1-4，点 P 是正方形 ABCD 的对角线 BD 上一点，PEBC于点 E，PFCD于点 F，连接 EF 给出 下列五个结论： AP

6、EF； APEF； APD一定是等腰三角形； PFEBAP； PDEC 其 中正确结论的番号是_ 图 1-3 图 1-4 （1）； （2）， ； （3）； （4）延长 FP 交 AB 于点 N，延长 AP 交 EF 于点 M，如右图 例题 1 A B D F EC P B A C Q P D D A C F E B H G C A B D P （1） 如图， 在正方形 ABCD 外取一点 E， 连接 AE、 BE、 DE 过点 A 作 AE 的垂线交 DE 于点 P 若A E A P ， PB 下列结论： APDAEB； 点 B 到直线 AE 的距离为； EBED； APDAPB SS； 正方

7、形ABCD S 其中正确结论的序号是（ ） A B C D （2）如图，正方形 ABCD 中，AC 是对角线，今有较大的直角三角板，一边始终经过点 B，直角顶点 P 在射线 AC 上移动，另一边交 DC 于 Q 、如图，当点 Q 在 DC 边上时，写出 PB 与 PQ 数量关系（直接写出结论） ； 、如图，当点 Q 落在 DC 延长线上时，写出 PB 与 PQ 的数量关系（直接写出结论） 图 图 （1）D； （2）PBPQ；证明：过 P 作PEBC，PFCD， P，C 为正方形对角线 AC 上的点， PC 平分DCB，DCB，PFPE， 四边形 PECF 为正方形， BPEQPE，QPEQPF

8、， BPEQPF，RtRtPQFPBE，PBPQ PBPQ；证明：过 P 作PEBC，PFCD， P，C 为正方形对角线 AC 上的点， PC 平分DCB，DCB， PFPE，四边形 PECF 为正方形， BPFQPF，BPFBPE， BPEQPF，RtRtPQFPBE，PBPQ 【教师备课提示】【教师备课提示】 例题 2 AB CD P Q AB CD Q P A E BC D P 相关结论 图例剖析 1 正方形对角线上任意一点到另外两个 顶点的距离相等，反之也成立； 2 过正方形对角线上任意一点构造直角 与正方形交于两点，此时形成的两条线 段必定相等，反之不成立 1EDEB，EBCEDC，

9、 AEBAED； 2若 FGFH，则 FG=FH （过 F 点 分别作 BC、CD 边的垂线，证明两个 直角三角形全等即可） 已知：如图，在矩形 ABCD 中，BE 平分ABC，CE 平分DCB，BF/CE，CF/BE求证：四边形 BECF 是正 方形 证明：BF/CE，CF/BE， 四边形 BECF 是平行四边形， 又在矩形 ABCD 中，BE 平分ABC，CE 平分DCB， EBAECB ， BEC ，BECE， 四边形 BECF 是正方形 模块二 弦图 （1）如图 4-1，四边形 ABCD 是正方形，直线 l、m、n 分别通过 A、B、C 三点，且/ / /lmn，若 l 与 m 的距

10、离为 5，m 和 n 的距离为 7，则正方形 ABCD 的面积为_ （2） （树德半期改编）如图 4-2，在ABC中，ACB ，ACBC，在DCE中，DCE ， DCEC ，ACD ，MNBE，则CM的长度为_ 图 4-1 图 4-2 （1）74； （2）7； 【点评】【点评】这道题主要是让学生们找到构造弦图的感觉第（2）题为正方形“婆罗摩笈多”中的“知垂直，证中 点” ， 利用弦图的方法可以求证， 分别过 A、 D 向 MN 作垂线即可， 而此题重点要向学生强调BECM 的结论 例题 3 例题 4 DC A l B m n C A B D EN M A ED B C F 模块三 垂直且相等模

11、型 如图， 正方形 ABCD 的边长为 6，AE ， O 是 AD 的中点， 且AE ， 那么EFG 的面积为_ 思路：作垂线构造全等， (ASA)EFIOGH， 则OGEFOE ， 且GOEF； 所以： 11 S EFGEFGO 已知正方形 ABCD 中，E 为对角线 BD 上一点，过点 E 作EFBD交 BC 于 F，连接 DF，G 为 DF 中点，连接 EG，CG （1）求证：EGCG，且EGCG； （2） 将图 6-1 中三角形 BEF 绕 B 点逆时针旋转， 如图 6-2 所示， 取 DF 中点 G， 连接 EG， CG， 求证：EGCG 且EGCG； （3）将图 6-2 中三角形

12、BEF 绕 B 点旋转任意角度，如图 6-3 所示，再连接相应的线段，问（2）中的结论是否 仍然成立？ 图 6-1 图 6-2 图 6-3 （1） DCBC，DCF为直角三角形 又G 为 DE 中点， CGDF ，且CGFCDG 同理EGDF ，且EGFEDG CG=EG，且EGC ，即EGCG （2）方法一：如图 1，延长 EG 交 AD 延长线于点 M，连接 CM、CE，易证DMGFEG、 BDEDCM，然后可证ECM为等腰直角三角形，于是EGCG，同时还可得EGCG； 方法二：如图 2，延长 CG 到 M，使得MGCG，连接 MF、ME、EC，类似方法一通过证两次全等和 一个等腰直角三角

13、形即可证得结论； 图3图2图1 A E B F C DA E B F C G D A E BF C G D 例题 5 例题 6 （3）结论为EGCG且EGCG，证明思路如下： 如图， 延长CG到M， 使得MGCG， 连接MF、 ME、 EC， 并延长MF交BC于点H， 先证MGFCGD， 再通过证明四边形 EBHF 对角互补证明EFMEBC ， 而可证EFMEBC及MEC为等腰直 角三角形，于是 EG=CG 且EGCG 【教师备课提示】【教师备课提示】这道题来源于母子型的变形，可以给同学们提一下 推导垂直且相等模型的结论 （1） （2） （3） 例题 7 1 如图 1-1， 在正方形 ABCD

14、 中， AC 为对角线， 点 E 在 AB 边上，EFAC于点 F， 连接 EC，AF ，EFC 的周长为 12，则 EC 的长为_ 2如图 1-2，以正方形 ABCD 的一边向正方形外作等边三角形 ABE，BD 与 EC 交于 F，则AFD等于（ ） A B C D 图 1-1 图 1-2 3如图 1-3，已知 E、F 分别是正方形 ABCD 的边 BC、CD 上的点，AE、AF 分别与对角线 BD 相交于 M、N， 若EAF ，则CMECNF_ 4若正方形 ABCD 的边长为 4，E 为 BC 边上一点，BE ，M 为线段 AE 上一点，射线 BM 交正 方形的一边于点 F，且BFAE，求

15、 BM 的长 5如图 1-5，AD 为正方形 ABCD 对角线，G 为对角线上任意一点，若 GFGE，且GF ，则GE _ 图 1-3 图 1-5 15；2A；3100；4 （如图 1）或 （如图 2） ；54 演练 1 D C A F E B AD E F B C D A F E B C N M A B F G C ED 图 1 图 2 6如图，正方形 ABCD 的边长为 5，直线l/l/l/l，且直线l和直线l之间的距离为 1，如果正方形 ABCD 的四个顶点分别在四条直线上 （1）证明：AEDCFB； （2）求直线l与l之间的距离 h （1）ADEAED ，ADEEDF ， EDFBFC

16、 ，AEDCFB ，易证AEDCFB （2） 方法一： 分别过A作直线l的垂线AH， 交l于点P， 由弦图易证AHBDPA BHAPh， 在ABH中，()hh ，解得h 方法二：分别过 B、D 作直线l的垂线，利用弦图证明全等即可 7如图，以ABC的边 AC、AB 为一边，分别向三角形的外侧作正方形 ACFG 和正方形 ABDE，连接 EG求 证： ABCAEG SS 思路一：过 B、E 分别作 AC、AG 的垂线， 只需证明BAQEAK得BQEK从而得证 证明：过 B 作 BQ 垂直 AC 的延长线于点 Q，过点 E 作 EK 垂直 AG 于 K EAKBAC，NACBAC， EAKBAQ

17、在ABQ和AEK中 BAQEAK AQBAKE ABAE ， ABQAEK，BQEK， 又 ABC SAC BQ ， AEG SAG EK ， ABCABC SS 思路二：将AEG绕点 A 旋转，使得点 A 是 BN 中点，从而得证 PH l4 l3 l2 l1 A B D C E F 1 P H 11 l4 l3 l2 l1 A B D C E FF E C D B A l1 l2 l3 l4 演练 2 演练 3 K Q E D BC A F G D G z E F BC A 证明：延长 BA 到 N，使ABAN，连结 CN显然 ABCACN SS EAGBAC，BAQBAC， EAGNAC

18、 在ACN和AGE中 EANA EAGNAC AGAC ， ACNAGE， ACNAGE SS， AEGACN SS 8已知 P 为等腰直角ABC的斜边 AB 上任意一点，PE、PF 分别为 AC、BC 之垂线，垂足为 E、FM 为 AB 之中点求证 E、M、F 组成等腰直角三角形 证明：延长 EM 至 N，使EMMN，连接 EF，FN，BN， 则AEMBNM，EMMN，AEBN，AMBN ， PEAC，PFBC，C ， 四边形 PECF 是矩形，CFPEAEBN，ACBC，CEBF， ABC ，MBN ，FBN FBNC ， 又CFBN，ECBF，ECFFBN，EFFN，FECNFB ， 又

19、FECEFC ，NFBEFC ， EFFN，又EFFN，EMMN， EMF是等腰直角三角形 【提示提示】连接 CM 利用直角三角形斜边中线会更简单 A B C E F P M N 演练 4 在三角形中最特殊的就是等边三角形，同样地，在四边形中也存在最特殊的平行四边形也就是正方形，而这 两个图形是我们数学中排名第二美和第三美的图形，排名第一美的就是我们以后要学习的圆。为什么老师说它们 是最美的呢？看看我们手里的一套尺子，有两个三角板、一个量角器和一个直尺，先说这两个三角板是怎么来的， 都来自于我们最美的图形，、的直角三角形其实来自等边三角形，是等边三角形的一半；、 的直角三角形来自于正方形，是正方形的一半；量角器也是来自于圆，是圆的一半。 思考问题：思考问题：给大家 4 个火柴棍，如何能拼出 5 个正方形呢？ 知 识 链 接 N G F A C B D E M P F E CB AA E CFB P M