《3.1.用树状图或表格求概率（第3课时）利用概率玩“配紫色”游戏》同步练习（含答案）

《《3.1.用树状图或表格求概率（第3课时）利用概率玩“配紫色”游戏》同步练习（含答案）》由会员分享，可在线阅读，更多相关《《3.1.用树状图或表格求概率（第3课时）利用概率玩“配紫色”游戏》同步练习（含答案）（10页珍藏版）》请在七七文库上搜索。

1、第 3 课时 利用概率玩“配紫色”游戏关键问答改变两个转盘的直径，对结果有影响吗？12017河南 如图 314 是一次数学活动课上制作的一个转盘，盘面被等分成四个扇形区域，并分别标有数字1，0，1，2.若转动转盘两次，每次转盘停止后记录指针所指区域的数字(当指针恰好指在分界线上时 ，不记，重转) ， 则记录的两个数字都是正数的概率为( )图 314A. B. C. D.18 16 14 122 如图 315，用两个转盘(其中一个转盘被分成两等份，另一个转盘被分成三等份)进行 “配紫色”游戏：分别转动两个转盘 ，若其中一个转盘转出了红色，另一个转盘转出了蓝色，则可配成紫色此时，配成紫色的概率是_

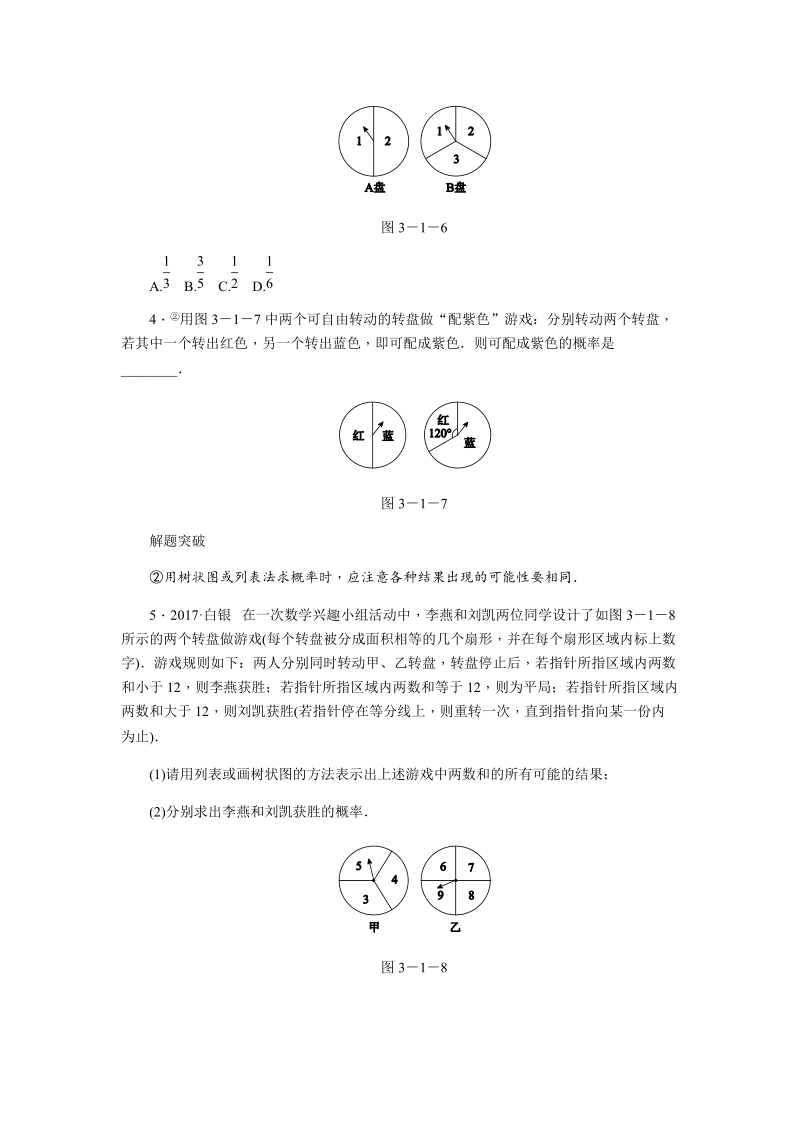
2、，出现相同颜色的概率是_图 315命题点 1 计算转盘事件中的概率 热度：89%32017深圳二模 如图 316，现分别旋转两个标准的转盘，则转盘所转到的两个数字之积为奇数的概率是( )图 316A. B. C. D.13 35 12 164 用图 317 中两个可自由转动的转盘做“配紫色”游戏：分别转动两个转盘，若其中一个转出红色，另一个转出蓝色，即可配成紫色则可配成紫色的概率是_图 317解题突破用树状图或列表法求概率时，应注意各种结果出现的可能性要相同52017白银 在一次数学兴趣小组活动中，李燕和刘凯两位同学设计了如图 318所示的两个转盘做游戏(每个转盘被分成面积相等的几个扇形，并在

3、每个扇形区域内标上数字)游戏规则如下：两人分别同时转动甲、乙转盘，转盘停止后，若指针所指区域内两数和小于 12，则李燕获胜；若指针所指区域内两数和等于 12，则为平局；若指针所指区域内两数和大于 12，则刘凯获胜( 若指针停在等分线上，则重转一次，直到指针指向某一份内为止) (1)请用列表或画树状图的方法表示出上述游戏中两数和的所有可能的结果；(2)分别求出李燕和刘凯获胜的概率图 318命题点 2 计算摸球事件中的概率 热度：87%6 在一个袋子中装有分别标注数字 1，2，3，4，5 的五个小球，这些小球除标注的数字不同外其余完全相同现从中随机取出 2 个小球，则取出的小球标注的数字之差的绝对

4、值为 2 或 4 的概率是( )A. B. C. D.110 310 25 14易错警示从一个袋子中取出 2 个小球，即同一个小球不可能取两次7 2017杭州 一个仅装有球的不透明布袋里共有 3 个球(只有颜色不同) ，其中 2 个是红球、1 个是白球，从中任意摸出一个球，记下颜色后放回，搅匀，再任意摸出一个球，则两次摸出的都是红球的概率是_解题突破本题与上一题都是从袋中取出两个球，两种取法的区别是什么？82017常州 一只不透明的袋子中装有 4 个大小、质地都相同的乒乓球，球面上分别标有数字 1，2，3，4.(1)搅匀后从中任意摸出 1 个球，求摸出的乒乓球球面上的数字为 1 的概率；(2)

5、搅匀后先从中任意摸出 1 个球( 不放回)，再从余下的 3 个球中任意摸出 1 个球，求两次摸出的乒乓球球面上的数字之和为偶数的概率命题点 3 概率在抽奖游戏中的应用 热度：80%9 某商场为了吸引顾客，设计了一个摸球获奖的箱子，箱子中共有 20 个球，其中红球 2 个、蓝球 3 个、黄球 5 个、白球 10 个，并规定购买 100 元的商品，就有一次摸球的机会，摸到红、蓝、黄、白球( 一次只能摸一个) 的顾客就可以分别得到 80 元、30 元、10元、0 元的购物券，凭购物券仍然可以在商场购物，如果顾客不愿意摸球，那么可以直接获得 10 元的购物券(1)每摸一次球所获购物券金额的平均值是多少

6、？(2)若你在此商场购买了 100 元的商品，两种方式中你会选择哪种方式？为什么？解题突破分别求出获得不同购物券的概率，把概率看作购物券的“权” ，利用加权平均数公式进行计算10 如图 319，这是某个小区内的道路示意图，小明家住在该小区的 A 处，他每天晚饭后都要从家出发随机沿着小区内的道路散步一圈后回家(每条道路不能重复走，有的道路可以不走)(1)利用树状图描述出小明散步的路线情况；(2)求小明散步经过点 E 的概率 P.图 319解题突破从 A 出发有三种可能的路径，在 B，D ，E 处分别有两种路径，按两步试验问题画树状图得到所有可能的路线情况11 如图 3110 是三个可以自由转动的

7、转盘，每个转盘被分成面积相等的几个扇形，并涂上图中所示的颜色小强和小亮用转盘 A 和转盘 B 做一个转盘游戏：同时转动两个转盘，如果转盘 A 转出了红色 ，转盘 B 转出了蓝色，或者转盘 A 转出了蓝色，转盘 B转出了红色，那么红色和蓝色在一起配成了紫色，这种情况下小强获胜；如果两个转盘转出的颜色相同，那么小亮获胜；在其他情况下，小强和小亮不分胜负(1)利用画树状图或列表的方法表示出此游戏所有可能出现的结果；(2)小强说：“此游戏不公平 ”请你帮小强说明理由；(3)请你在转盘 C 的空白处，涂上适当颜色，使得用转盘 C 替换转盘 B 后，游戏对小强和小亮是公平的(只需在空白处填写表示颜色的文字

8、即可，不要求说明理由) 图 3110解题突破所谓游戏公平，就是游戏双方获胜的概率相同详解详析【关键问答】改变两个转盘的直径，对结果没有影响1C 解析 画树状图如下：共有 16 种等可能的结果，两个数字都是正数的有 4 种情况，两个数字都是正数的概率是 .416 14故选 C.2. 解析 列表如下：13 13红 蓝蓝 (红，蓝) (蓝，蓝)黄 (红，黄) (蓝，黄)红 (红，红) (蓝，红)一共有 6 种等可能的结果，配成紫色的有 2 种情况，出现相同颜色的有 2 种情况，配成紫色的概率是 ，出现相同颜色的概率是 .26 13 26 133A 解析 画树状图如下：共有 6 种等可能的结果，转盘所

9、转到的两个数字之积为奇数的有 2 种情况，转盘所转到的两个数字之积为奇数的概率是 .故选 A.26 134. 解析 将第二个转盘中的蓝色部分等分成两部分， 画树状图如下：12共有 6 种等可能的结果，可配成紫色的有 3 种情况，可配成紫色的概率是 .125解：(1)根据题意列表如下：甲 和 乙 6 7 8 93 9 10 11 124 10 11 12 135 11 12 13 14由上表可知，两数和共有 12 种等可能的结果(2)由(1)可知，两数和共有 12 种等可能的结果，其中和小于 12 的情况有 6 种，和大于12 的情况有 3 种，李燕获胜的概率为 ，刘凯获胜的概率为 .612 1

10、2 312 146C 解析 画树状图如下：共有 20 种等可能的结果，取出的小球标注的数字之差的绝对值为 2 或 4 的有 8 种情况，取出的小球标注的数字之差的绝对值为 2 或 4 的概率是 .故选 C.820 257. 解析 根据题意画出树状图如下：49所以一共有 9 种等可能的结果，两次摸到红球的有 4 种情况，所以两次摸出的都是红球的概率是 .498解：(1)共有 4 个大小、质地都相同的乒乓球，球面上分别标有数字1，2，3，4，摸出的乒乓球球面上的数字为 1 的概率是 .14(2)根据题意画树状图如下：共有 12 种等可能的结果，两次摸出的乒乓球球面上的数字之和为偶数的有 4 种情况

11、，则两次摸出的乒乓球球面上的数字之和为偶数的概率为 .412 139解：(1)P(摸到红球) ，P(摸到蓝球) ，P(摸到黄球) ，P( 摸到白球)220 320 520，1020每摸一次球所获购物券金额的平均值是 80 30 10 15(元) 220 320 520(2)选择摸球方式理由：1510，两种方式中我会选择摸球这种方式，此时较合算10解：(1)画树状图如下：则共有 6 种等可能的结果(2)小明散步经过点 E 的有 4 种情况，小明散步经过点 E 的概率 P .46 2311解：(1)画树状图得所有可能出现的结果如下：则共有 15 种等可能出现的结果(2)配成紫色的有 3 种情况，颜色相同的有 4 种情况，P(小强获胜) ，P(小亮获胜) .315 15 415P(小强获胜)P(小亮获胜)，此游戏不公平(3)如图，此时 P(小强获胜)P(小亮获胜) .15故此游戏对小强和小亮是公平的