8.3.1棱柱、棱锥、棱台的表面积和体积ppt课件

《8.3.1棱柱、棱锥、棱台的表面积和体积ppt课件》由会员分享，可在线阅读，更多相关《8.3.1棱柱、棱锥、棱台的表面积和体积ppt课件（25页珍藏版）》请在七七文库上搜索。

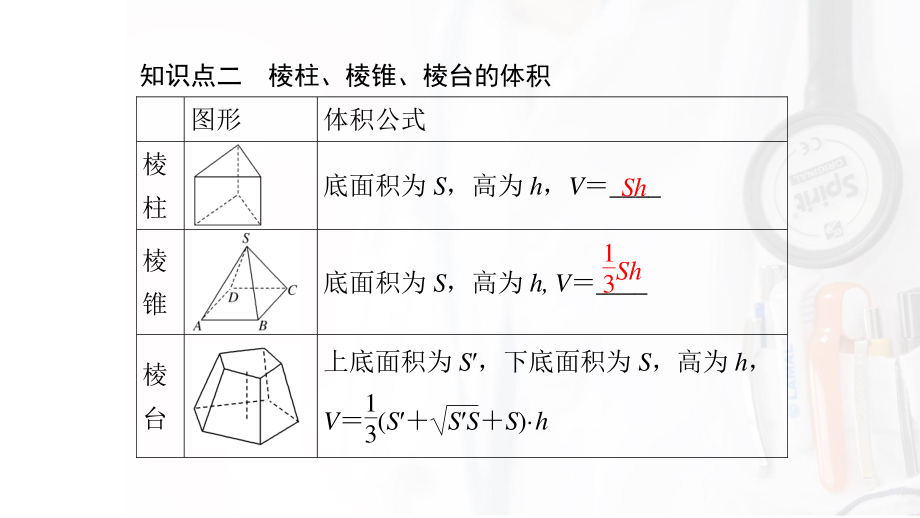
1、8.3.1 棱柱、棱锥、棱台的表面积和体积 知识点一 棱柱、棱锥、棱台的表面积 棱柱、棱锥、棱台都是由多个_图形围成的多面体，因此它们的表面积等于_的面积之和，也就是_的面积 平面 各个面 展开图 【新知初探】 知识点二 棱柱、棱锥、棱台的体积 图形 体积公式 棱 柱 底面积为 S，高为 h，V_ 棱 锥 底面积为 S，高为 h, V_ 棱 台 上底面积为 S，下底面积为 S，高为 h， V13(S SSS) h Sh 13Sh 状元随笔 (1)多面体展开图的面积即为多面体的表面积，在实际计算中，只要弄清楚多面体的各个面的形状并计算其面积，然后求其和即可，一般不把多面体真正展开 (2)等底、等

2、高的两个柱体的体积相同 (3)求台体的体积转化为求锥体的体积 根据台体的定义进行“补形”， 还原为锥体， 采用“大锥体”减去“小锥体”的方法求台体的体积 教材解难 教材思考 观察棱柱、棱锥、棱台的体积公式 V棱柱Sh，V棱锥13Sh，V棱台13h(S SSS)，它们之间有什么关系？你能用棱柱、棱锥、棱台的结构特征来解释这种关系吗？ 提示：根据以上关系，在台体的体积公式中，令 S S，得柱体的体积公式；令 S 0，得锥体的体积公式，其关系如图： 1边长为 1 的正方体的表面积为( ) A4 B6 C8 D12 解析：正方体一个面的面积为 1，六个面的面积为 6. 答案：B 【基础自测】 2 三棱

3、锥 VABC 底面是边长为 2 的正三角形， 高为 3，求三棱锥的体积( ) A. 3 B2 3 C3 3 D.2 33 解析：底面是正三角形，边长为 2，则面积为 3， V13Sh13 3 3 3. 答案：A 3若棱台的上、下底面面积分别为 4,16，高为 3，则该棱台的体积为( ) A26 B28 C30 D32 解析：所求棱台的体积 V13(416 416)328. 答案：B 4.某几何体的直观图如图所示(单位： cm)， 则该几何体的表面积是_ cm2，体积是_ cm3. 解析： 由直观图可得该几何体是由一个长、 宽、 高分别为4 cm、4 cm、2 cm 的长方体和一个棱长为 2 的

4、正方体组合而成的，故表面积为 S44242422480(cm2)， 体积为 V44222240(cm3) 答案：80 40 题型一 多面体的表面积经典例题 例 1 底面为正方形的直棱柱，它的底面对角线长为 2，体对角线长为 6，则这个棱柱的侧面积是( ) A.2 B4 C6 D8 【解析】 由已知得底面边长为 1，侧棱长为 622. S侧1 2 48. 【答案】 D 【课堂探究】 方法归纳 1多面体的表面积转化为各面面积之和 2解决有关棱台的问题时，常用两种解题思路：一是把基本量转化到梯形中去解决；二是把棱台还原成棱锥，利用棱锥的有关知识来解决 跟踪训练 1 如图所示， 设正三棱锥 SABC

5、的侧面积是底面积的 2 倍，正三棱锥的高 SO3，则此三棱锥的表面积为_ 解析：设正三棱锥的底面边长为 a，斜高为 h，过点 O 作OEAB，交 AB 于点 E，连接 SE，则 SEAB，SEh. S侧2S底，312ah234a2，a 3h. SOOE，SO2OE2SE2，3236 3h2h2， h2 3，a 3h6. S底34a234 629 3，S侧2S底18 3. S表S侧S底18 39 327 3. 答案：27 3 题型二 多面体的体积经典例题 例 2 一个正三棱锥的底面边长为 6，侧棱长为 15，求这个正三棱锥的体积_ 【解析】 如图所示为正三棱锥SABC.设H为正三角形ABC的中心

6、，连接 SH，则 SH 即为该正三棱锥的高连接 AH 并延长交 BC 于 E，则 E 为 BC 的中点，且 AEBC. ABC 是边长为 6 的正三角形， AE32 63 3，AH23AE2 3. 在 RtSHA 中，SA 15，AH2 3， SH SA2AH2 1512 3. 在ABC 中，SABC12BC AE12 6 3 39 3， VSABC13 9 3 39，即这个正三棱锥的体积为 9. 【答案】 9 状元随笔 求棱锥的体积关键是求其高，需要在正棱锥的特征三角形中求解. 方法归纳 1常见的求几何体体积的方法 公式法：直接代入公式求解等积法：如四面体的任何一个面都可以作为底面，只需选用

7、底面积和高都易求的形式即可分割法：将几何体分割成易求解的几部分，分别求体积 2求几何体体积时需注意的问题 柱、锥、台的体积的计算，一般要找出相应的底面和高，要充分利用截面、轴截面，求出所需要的量，最后代入公式计算 跟踪训练 2 如图，正方体 ABCDA1B1C1D1的棱长为 1，E 为线段 B1C 上的一点，则三棱锥 ADED1的体积为_ 解析：三棱锥 ADED1的体积等于三棱锥 EDD1A 的体积， 即 VADED1VEDD1A1312 1 1 116. 答案：16 题型三 空间组合体的表面积和体积 例 3 如图，一个漏斗的上面部分是一个长方体，下面部分是一个四棱锥，两部分的高都是 0.5

8、m，公共面 ABCD 是边长为 1 m的正方形，那么这个漏斗的容积是多少立方米(精确到 0.01 m3)? 解：由题意知 V长方体ABCDABCD1 1 0.50.5(m3)， V棱锥PABCD13 1 1 0.516(m3) 所以这个漏斗的容积 V1216230.67(m3). 方法归纳 求组合体的表面积与体积，关键是弄清楚组合体是由哪几种简单几何体组合而成的，然后由相应几何体的表面积与体积相加或相减得出需要注意，组合体的表面积并不是简单几何体的表面积的和，因为其接合部分并不裸露在表面 跟踪训练 3 已知某几何体的直观图如图所示(单位： cm)，求这个几何体的表面积和体积 解：这个几何体可看成是正方体 ABCDA1B1C1D1与直三棱柱 B1C1QA1D1P 的组合体 由 PA1PD1 2，A1D1AD2，可得 PA1PD1. 故所求几何体的表面积 S5 222 2 2212 ( 2)2(224 2)(cm2)， 体积 V2312 ( 2)2 210(cm3)