北京市燕山区2021—2022学年度七年级上期末数学试卷（含答案）

《北京市燕山区2021—2022学年度七年级上期末数学试卷（含答案）》由会员分享，可在线阅读，更多相关《北京市燕山区2021—2022学年度七年级上期末数学试卷（含答案）（7页珍藏版）》请在七七文库上搜索。

1、燕山地区 20212022 学年第一学期七年级期末质量监测 数数 学学 试试 卷卷 2022 年 1 月 考 生 须 知 1本试卷共 6 页，共三道大题，25 道小题，满分 100 分。考试时间 100 分钟。 2在试卷和答题纸上准确填写学校名称、班级、姓名和考号。 3试题答案一律填涂或书写在答题纸上，在试卷上作答无效。 4在答题纸上，选择题、画图题用 2B 铅笔作答，其他试题用黑色字迹签字笔作答。 5考试结束，请将答题纸和试卷一并交回。 一、选择题（本题共一、选择题（本题共 24 分分，每每小题小题 3 分）分） 第第 18 题均有四个选项，符合题意的选项题均有四个选项，符合题意的选项只有一

2、个只有一个 12022 的相反数是 A2022 B2022 C12022 D12022 2根据北京市“十四五”信息通信行业发展规划，预计到 2025 年末，北京市将建成并开通 5G 基站63000 个，基本实现对城市、乡镇、行政村和主要道路的连续覆盖将 63000 用科学记数法表示应为 A63 103 B6.3 103 C6.3 104 D0.63 105 3已知 x1 是关于 x 的一元一次方程 x2a0 的解，则 a 的值是 A2 B2 C12 D12 4下列各组中的两个单项式是同类项的是 A3 与a B22a b与23 a b C33a与22a D32a b与2312a b 5有理数 a

3、 在数轴上的对应点的位置如图所示，若有理数 b 满足ba，则 b 的值不可能是 A3 B1 C0 D2 6已知A 与B 互余，A56 15，则B A34 45 B33 45 C124 45 D123 45 7右面的框图表示解方程1824xx的流程，其中第步和第步变形的依据相同，这两步变形的依据是 A乘法分配律 B分数的基本性质 C等式的两边加(或减)同一个数，结果仍相等 D等式的两边乘同一个数，或除以同一个不为 0 的数，结果仍相等 第步 去分母 第步 去括号 第步 移项 2(x1)8x 2x28x 2xx82 3x6 x2 第步 系数化为 1 第步 合并同类项 8我国明朝数学家程大位所著的算

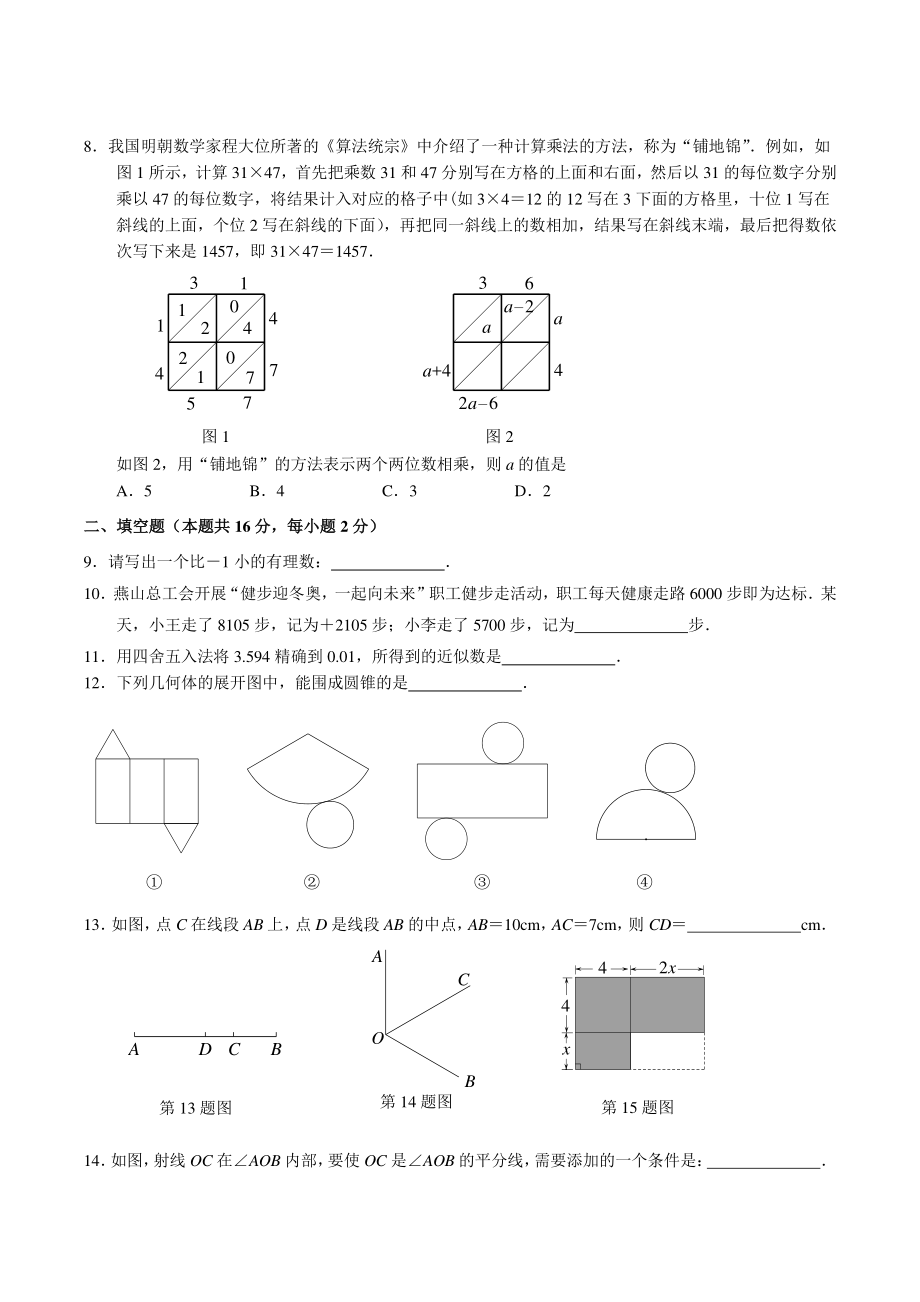
4、法统宗中介绍了一种计算乘法的方法，称为“铺地锦” 例如，如图 1 所示，计算 3147，首先把乘数 31 和 47 分别写在方格的上面和右面，然后以 31 的每位数字分别乘以 47 的每位数字，将结果计入对应的格子中(如 3412 的 12 写在 3 下面的方格里，十位 1 写在斜线的上面，个位 2 写在斜线的下面） ，再把同一斜线上的数相加，结果写在斜线末端，最后把得数依次写下来是 1457，即 31471457 如图 2，用“铺地锦”的方法表示两个两位数相乘，则 a 的值是 A5 B4 C3 D2 二、二、填空题（本题共填空题（本题共 16 分，每小题分，每小题 2 分）分） 9请写出一个

5、比1 小的有理数： 10燕山总工会开展“健步迎冬奥，一起向未来”职工健步走活动，职工每天健康走路 6000 步即为达标某天，小王走了 8105 步，记为2105 步；小李走了 5700 步，记为 步 11用四舍五入法将 3.594 精确到 0.01，所得到的近似数是 12下列几何体的展开图中，能围成圆锥的是 13 如图， 点 C 在线段 AB 上， 点 D 是线段 AB 的中点， AB10cm， AC7cm， 则 CD cm 14 如图， 射线 OC 在AOB 内部， 要使 OC 是AOB 的平分线， 需要添加的一个条件是： 7514072104127413图 1 图 2 a+4a2a36a4

6、2a6442xx第 15 题图 CBAO第 14 题图 CBAD第 13 题图 15图中的四边形均为长方形，请用含 x 的代数式表示出图中阴影部分的面积 16周末，小康一家和姑姑一家(共 6 人)相约一起去观看电影长津湖小康用手机查到家附近两家影城的票价和优惠活动如下： 影城 票价(元) 优惠活动 时光影城 48 学生票半价 遇见影城 50 网络购票，总价打八折 小康利用网络给所有人都购了票，他发现在两家影城购票的总费用相同，则购票的总费用是 元，两家共有学生 人 三、三、解答题解答题（本题共（本题共 60 分，分，第第 1718 题，题，每题每题各各 8 分分，每小题，每小题 4 分；第分；

7、第 19 题题10 分分，每小题，每小题 5 分；第分；第 2022题，题，每题每题各各 5 分分；第；第 2324 题，题，每题每题各各 6 分分；第；第 25 题题 7 分）分） 解答应写出文字说明、证明过程或演算步骤解答应写出文字说明、证明过程或演算步骤 17计算： (1) |5|(3)(2)； (2) 33(1913)(4)(2) 18化简： (1) 5324abab； (2) 223(21)2(2 )3aaaa 19解方程： (1) 53 11 2xx； (2)1123xx 20求代数式22212432233xyyxy()()的值，其中 x2，y1 21如图，已知MON60 ，点 A

8、 在射线 OM 上，点 B 在射线 ON 下方请选择合适的画图工具按要求画图并回答问题(要求：不写画法，保留画图痕迹) (1) 过点 A 作直线 l，使直线 l 只与MON 的一边相交； (2) 在射线 ON 上取一点 C， 使得 OCOA， 连接 AC， 度量OAC 的大小为 ； （精确到度） (3) 在射线 ON 上作一点 P，使得 APBP 最小，作图的依据是 MAOBN 22列列一元一次一元一次方程解应用题方程解应用题： “共和国勋章”获得者，“杂交水稻之父”袁隆平院士一生致力于提高水稻的产量，为解决人类温饱问题做出了巨大贡献某农业基地现有 A，B 两块试验田各 20 亩，A 块种植普

9、通水稻，B 块种植杂交水稻， 两块试验田单次共收获水稻 33600 千克 已知杂交水稻的亩产量是普通水稻亩产量的 1.8倍 求杂交水稻的亩产量是多少千克？ 23如图，数轴上点 A，B，M，N 表示的数分别为1，5，m，n，且 AM23AB，点 N 是线段 BM 的中点，求 m，n 的值 24如图，点 O 在直线 AB 上，COD60 ，射线OE 在COD 内部， 且AOE2DOE (1)如图 1， 若 OD 是BOC的平分线， 求COE的度数； 下面是下面是小宇小宇同学的同学的解答过程解答过程, ,请请帮小宇补帮小宇补充完整充完整 解：如图 1， OD 是BOC 的平分线， BOD 60 ，

10、AOD180 BOD120 AODAOEDOE，AOE2DOE， AOD3 ， DOE13AOD40 ， COE DOE20 (2) 如图 2，小宇发现当BOD 的大小发生变化时，COE 与BOD 的数量关系保持不变，请你用等式表示出COE 与BOD 的数量关系，并说明理由 25我们规定：使得ab ab 成立的一对数 a，b 为“积差等数对” ，记为(a，b)例如，因为 1.50.61 . 5 0 . 6 ， ( 2 ) 2 ( 2 ) 2 ， 所 以 数 对 ( 1 . 5 ， 0 . 6 ) ， ( 2 ， 2 ) 都 是 “积差等数对” -543-11xAB02-2-4 -35图 2 B

11、OACDE图 1 EDCABO(1) 下列数对中，是“积差等数对”的是 ； (2，23)； (1.5，3)； (12，1) (2) 若(k，3)是“积差等数对” ，求 k 的值； (3) 若(m，n)是“积差等数对” ，求代数式22432(1)2(32 )6mnmmnmnm的值 参考参考答案及评分答案及评分标准标准 一、选择题（本题共一、选择题（本题共 24 分分，每每小题小题 3 分）分） 题号 1 2 3 4 5 6 7 8 选项 A C D B A B D A 二、二、填空题（本题共填空题（本题共 16 分，每小题分，每小题 2 分）分） 9答案不唯一，如，2，3.5； 10300； 1

12、13.59； 12； 132； 14答案不唯一，如，AOCBOC，AOC12AOB，AOB2AOC； 1512x16； 16240，2 三、三、解答题解答题（本题共（本题共 60 分，分，第第 1718 题，题，每题每题各各 8 分分，每小题，每小题 4 分；第分；第 19 题题10 分分，每小题，每小题 5 分；第分；第 2022题，题，每题每题各各 5 分分；第；第 2324 题，题，每题每题各各 6 分分；第；第 25 题题 7 分）分） 17解：(1)原式532 2 分 10 4 分 (2)原式27(1913)2 或 原式27(1939)2 2 分 271927132 27492 3

13、分 392 122 14 14 4 分 18解：(1)原式5243aabb() () 2 分 3ab 4 分 (2)原式22633243aaaa 2 分 247aa 4 分 19解：(1)移项，得 5x2x113， 2 分 合并同类项，得 7x14， 4 分 系数化为 1，得 x2 5 分 (2)去分母，得 3(x1)62x， 1 分 去括号，得 3x362x， 2 分 移项，得 3x2x63， 3 分 合并同类项，得 5x9， 4 分 系数化为 1，得 x95 5 分 20解：原式2221442223333xyyxy 3 分 2222xy 4 分 当 x2，y1 时， 原式2222( 1)2

14、 422 0 5 分 21解：(1) 作直线 l，如图； 1 分 (2) 作点 C，连接 AC，如图； OAC 60 ； 3 分 (3) 作点 P， 如图； 两点之间，线段最短 5分 22解：设普通水稻亩产量为x千克，则杂交水稻的亩产量是 1.8x千克， 1 分 根据题意，得 20 x201.8x33600， 2 分 解方程，得 600 3 分 1.8x1.86001080 千克 4 分 答：杂交水稻的亩产量是 1080 千克 5 分 23解：数轴上，点 A，B 表示的数分别为1，5， AB6 1 分 AM23AB， AM4 2 分 当点 M 在点 A 右侧时， 点 A 表示的数为1，AM4，

15、 点 M 表示的数为 3，即 m3 点 B 表示的数为 5，点 N 是线段 BM 的中点， 点 N 表示的数为 4，即 n4 当点 M 在点 A 左侧时， xMAOBNPlC5-3-4-220BAx1-134-5M2N2N1M1点 A 表示的数为1，AM4， 点 M 表示的数为5，即 m5 点 B 表示的数为 5，点 N 是线段 BM 的中点， 点 N 表示的数为 0，即 n0 综上，m3，n4，或 m5，n0 6 分 24解：(1)COD，DOE，COD； 3 分 (2) BOD3COE 4 分 理由如下：如图，设COE ， COD60 ， DOECODCOE60 (60) AOE2DOE，AODAOEDOE， AOD3DOE3(60) (1803) ， BOD180 AOD180 (1803) 3 ， BOD3COE 6 分 25解：(1) 2 分 (2) (k，3)是“积差等数对” ， k(3)k(3)， 3 分 即 k33k， 解得 k34 4 分 (3) (m，n)是“积差等数对” ， m n mn ， ， 224(322)646mnmmnmnm 4(2)4mnmn 4484mnmn 44()8mnmn 448mnmn 8 7 分 22432(1)2(32 )6mnmmnmnmBOACDE