 2022年北京市中考仿真模拟数学试卷(1)含答案解析
2022年北京市中考仿真模拟数学试卷(1)含答案解析
《2022年北京市中考仿真模拟数学试卷(1)含答案解析》由会员分享,可在线阅读,更多相关《2022年北京市中考仿真模拟数学试卷(1)含答案解析(23页珍藏版)》请在七七文库上搜索。
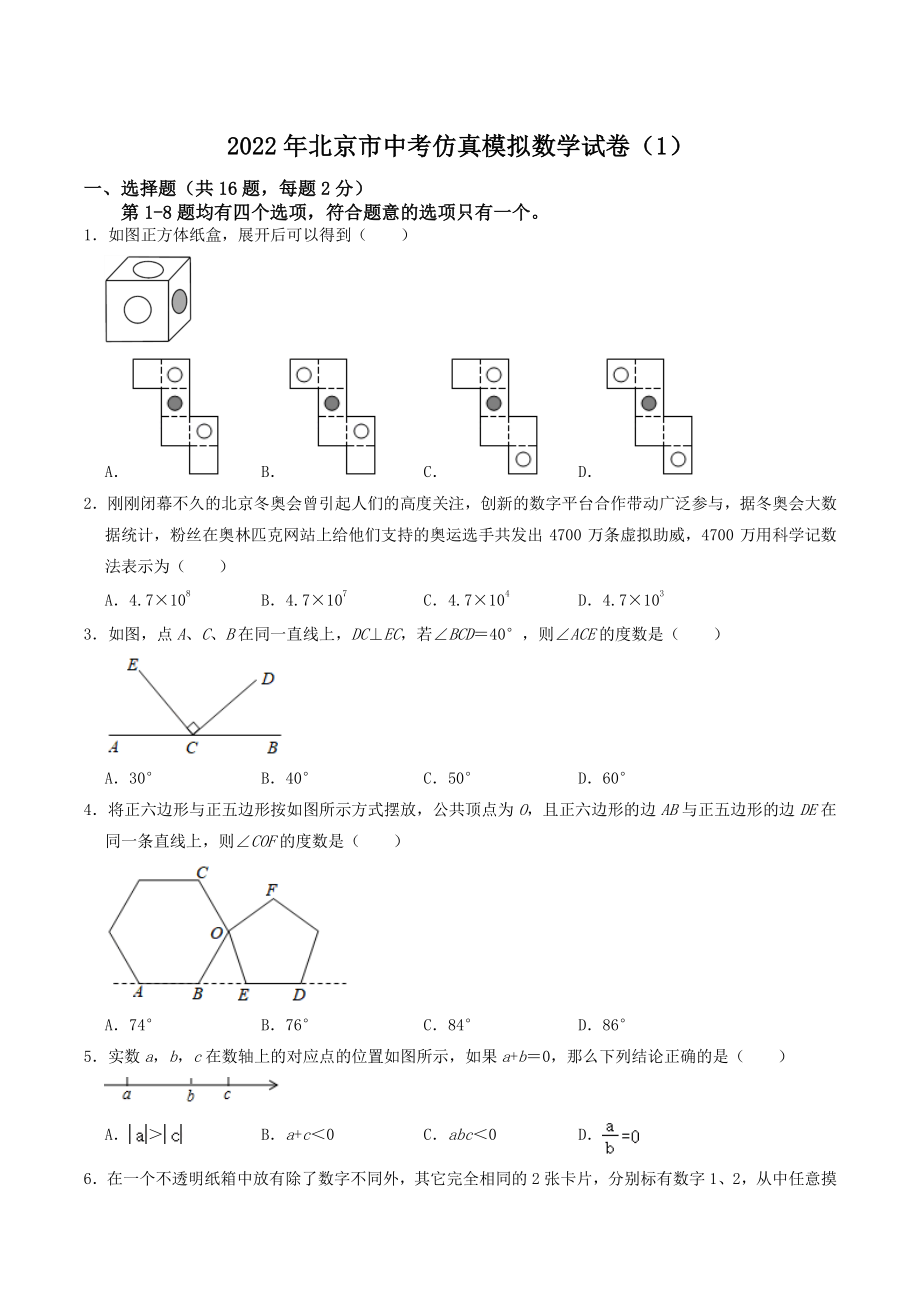
1、20222022 年北京市中考仿真模拟数学试卷(年北京市中考仿真模拟数学试卷(1 1) 一、一、选择题(共选择题(共 1616 题,每题题,每题 2 2 分)分) 第第 1 1- -8 8 题均有四个选项,符合题意的选项只有一个。题均有四个选项,符合题意的选项只有一个。 1如图正方体纸盒,展开后可以得到( ) A B C D 2刚刚闭幕不久的北京冬奥会曾引起人们的高度关注,创新的数字平台合作带动广泛参与,据冬奥会大数据统计,粉丝在奥林匹克网站上给他们支持的奥运选手共发出 4700 万条虚拟助威,4700 万用科学记数法表示为( ) A4.7108 B4.7107 C4.7104 D4.7103
2、 3如图,点A、C、B在同一直线上,DCEC,若BCD40,则ACE的度数是( ) A30 B40 C50 D60 4将正六边形与正五边形按如图所示方式摆放,公共顶点为O,且正六边形的边AB与正五边形的边DE在同一条直线上,则COF的度数是( ) A74 B76 C84 D86 5实数a,b,c在数轴上的对应点的位置如图所示,如果a+b0,那么下列结论正确的是( ) A Ba+c0 Cabc0 D 6在一个不透明纸箱中放有除了数字不同外,其它完全相同的 2 张卡片,分别标有数字 1、2,从中任意摸出一张,放回搅匀后再任意摸出一张,两次摸出的数字之和为奇数的概率为( ) A B C D 7已知a
3、,b是两个连续整数,a1b,则a,b分别是( ) A2,1 B1,0 C0,1 D1,2 8对于向上抛出的物体,在没有空气阻力的条件下,满足这样的关系式:hvtgt2,其中h是上升高度,v是初始速度,g为重力加速度(g10m/s2) ,t为抛出后的时间若v20m/s,则下列说法正确的是( ) A当h20m时,对应两个不同的时刻点 B当h25 m时,对应一个时刻点 C当h15m时,对应两个不同的时刻点 Dh取任意值,均对应两个不同的时刻点 二、填空题(共二、填空题(共 1616 分,每题分,每题 2 2 分)分) 9若二次根式在实数范围内有意义,那么x的取值范围是 10因式分解:3mx2+6mx
4、+3m 11的解是 12若反比例函数的图象经过点A(2,4)和点B(8,a) ,则a的值为 13如图,PA、PB是O的两条切线,切点分别为A、B,连接AB若O的半径为 2,且PA4,则PAB的面积是 14如图,矩形ABCD中,AC,BD相交于点O,过点B作BFAC交CD于点F,交AC于点M,过点D作DEBF交AB于点E,交AC于点N,连接FN,EM则下列结论: DNBM;EMFN;AEFC;当AOAD时,四边形DEBF是菱形 其中,正确的序号为: 15甲、乙两人参加射击比赛,下表记录了两人连续 5 次的射击成绩通过这 5 次成绩,可以看出成绩比较稳定的是 (填“甲”或“乙” ) 次数 环数 1
5、 2 3 4 5 甲 2 6 7 7 8 乙 3 5 6 8 8 16一个旅行者从某地出发,他先走平路,然后爬山,到了山顶后立即沿原路下山,再走平路,回到出发地若他在平路上每小时走 4km,爬山时每小时走 3km,下山时每小时走 6km,他共走了 5 小时,则他共走了 km 三、解答题(共三、解答题(共 6868 分,第分,第 1717- -2020 题,每题题,每题 5 5 分,第分,第 2121- -2222 题,每题题,每题 6 6 分,第分,第 2323 题题 5 5 分,第分,第2424 题题 6 6 分,第分,第 2525 题题 5 5 分,第分,第 2626 题题 6 6 分,第
6、分,第 2727- -2828 题,每题题,每题 7 7 分)分) 17计算:|1|+6cos30(2021)0 18解一元一次不等式组: 19先化简,再求值: (x+1) (x3)(x+2) (x2)+x(x4) ,其中x26x+70 20图、图均是 56 的正方形网格,每个小正方形的顶点称为格点,小正方形的边长为 1,点A、E、F均在格点上在图、图中,只用无刻度的直尺,在给定的网格中按要求画图,所画图形的顶点均在格点上,不要求写出画法 (1)在图中画一个正方形ABCD,使其面积为 5 (2)在图中画一个等腰EFG,使EF为其底边 21已知关于x的一元二次方程x2(2k+1)x+k2+k0
7、(1)求证:无论k取何值,方程都有两个不相等的实数根 (2)如果方程的两个实数根为x1,x2,且k与都为整数,求k所有可能的值 22如图,在ABCD中,E,F是对角线BD上的两点(点E在点F左侧) ,且AEBCFD90 (1)求证:四边形AECF是平行四边形; (2)当AB5,tanABE,CBEEAF时,求BD的长 23在平面直角坐标系xOy中,一次函数ykx+b(k0)的图象由函数的图象向下平移 2 个单位长度得到 (1)求这个一次函数的解析式; (2)当x4 时,对于x的每一个值,函数ymx(m0)的值大于一次函数ykx+b的值,直接写出m的取值范围 24如图,RtABC中,C90,M为
8、AB上一点,过M,C,B三点的O交AC于P,过点P作PDAB,交O于点D (1)若M是AB中点,连接MD,求证:四边形APDM是平行四边形; (2)连接PM,当PMPC,且AC4,tanA,求线段PD的长 25某校组织了一次关于“金砖 5 国”的知识竞赛,根据获奖的同学们在竞赛中的成绩制成了如图的频数分布直方图,已知组别 95x100 的频率为 0.1请仔细阅读图表解答问题: (1)计算这次获奖的总人数,并补全分数分布直方图 (2)获奖的中位数在哪个分数段? (3)请估算这些获奖同学的成绩平均分 26已知抛物线yax22x+3 经过点A(2,3) (1)求a的值和图象的顶点坐标 (2)若点B(
9、m,n)在该抛物线上,且2m2,求n的取值范围 27 如图 1, 在 RtABC和 RtDPC中, ACBDCP90,ACDCBCPC,AB与DC交于Q,DP与AB、BC分别交于E、F (1)求证:CQCF (2)如图 2,RtABC不动,将 RtDPC绕点C旋转到BCD45时,判断四边形ACPE的形状,并证明你的结论 28如图,四边形ABCD中,BC90,点E为BC中点,AEDE于点E点O是线段AE上的点,以点O为圆心,OE为半径的O与AB相切于点G,交BC于点F,连接OG (1)求证:ECDABE; (2)求证:O与AD相切; (3)若BC6,AB3,求O的半径和阴影部分的面积 20222
10、022 年北京市中考仿真模拟数学试卷(年北京市中考仿真模拟数学试卷(1 1) 一、一、选择题(共选择题(共 1616 题,每题题,每题 2 2 分)分) 第第 1 1- -8 8 题均有四个选项,符合题意的选项只有一个。题均有四个选项,符合题意的选项只有一个。 1如图正方体纸盒,展开后可以得到( ) A B C D 解:根据题意可知,有两个白色圆的面与有黑色圆的面相邻且有公共顶点 答案:A 2刚刚闭幕不久的北京冬奥会曾引起人们的高度关注,创新的数字平台合作带动广泛参与,据冬奥会大数据统计,粉丝在奥林匹克网站上给他们支持的奥运选手共发出 4700 万条虚拟助威,4700 万用科学记数法表示为(
11、) A4.7108 B4.7107 C4.7104 D4.7103 解:4700 万470000004.7107 答案:B 3如图,点A、C、B在同一直线上,DCEC,若BCD40,则ACE的度数是( ) A30 B40 C50 D60 解:DCEC, ECD90, BCD40, ACE180904050 答案:C 4将正六边形与正五边形按如图所示方式摆放,公共顶点为O,且正六边形的边AB与正五边形的边DE在同一条直线上,则COF的度数是( ) A74 B76 C84 D86 解:由题意得:EOF108,BOC120,OEB72,OBE60, BOE180726048, COF36010848
12、12084, 答案:C 5实数a,b,c在数轴上的对应点的位置如图所示,如果a+b0,那么下列结论正确的是( ) A Ba+c0 Cabc0 D 解:a+b0, a、b互为相反数,a0bc,|a|b|c|, A选项错误; a+c要取绝对值较大的数的符号, a+c0, B选项错误; a0bc, abc0, C选项正确; a、b互为相反数, 1, D选项错误, 答案:C 6在一个不透明纸箱中放有除了数字不同外,其它完全相同的 2 张卡片,分别标有数字 1、2,从中任意摸出一张,放回搅匀后再任意摸出一张,两次摸出的数字之和为奇数的概率为( ) A B C D 解:画树状图如下: 共有 4 种等可能的
13、结果,两次摸出的数字之和为奇数的结果有 2 种, 两次摸出的数字之和为奇数的概率为, 答案:C 7已知a,b是两个连续整数,a1b,则a,b分别是( ) A2,1 B1,0 C0,1 D1,2 解:134, 12, 011, a0,b1 答案:C 8对于向上抛出的物体,在没有空气阻力的条件下,满足这样的关系式:hvtgt2,其中h是上升高度,v是初始速度,g为重力加速度(g10m/s2) ,t为抛出后的时间若v20m/s,则下列说法正确的是( ) A当h20m时,对应两个不同的时刻点 B当h25 m时,对应一个时刻点 C当h15m时,对应两个不同的时刻点 Dh取任意值,均对应两个不同的时刻点
14、解:hvtgt2,v20m/s,g10m/s2, h20t5t2 5(t24t) 5(t2)2+20, 当t2s时,h有最大值为 20m,即物体能达到的最大高度为 20m,且h20m时,只有一个时刻, A、B、D均不正确 h20t5t2为开口向下的二次函数,h有最大值为 20m, 当h15m时,对应两个不同的时刻点 C正确 答案:C 二、填空题(共二、填空题(共 1616 分,每题分,每题 2 2 分)分) 9若二次根式在实数范围内有意义,那么x的取值范围是 x 解:由题意得: 32x0, x, 答案:x 10因式分解:3mx2+6mx+3m 3m(x+1)2 解:原式3m(x2+2x+1)


- 配套讲稿:
如PPT文件的首页显示word图标,表示该PPT已包含配套word讲稿。双击word图标可打开word文档。
- 特殊限制:
部分文档作品中含有的国旗、国徽等图片,仅作为作品整体效果示例展示,禁止商用。设计者仅对作品中独创性部分享有著作权。
- 关 键 词:
- 2022 北京市 中考 仿真 模拟 数学试卷 答案 解析
 七七文库所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
七七文库所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。



 浙公网安备33030202001339号
浙公网安备33030202001339号
链接地址:https://www.77wenku.com/p-211999.html