 第13讲旋转中的最值路径长 讲义(学生版+教师版)2022年人教版九年级数学上册
第13讲旋转中的最值路径长 讲义(学生版+教师版)2022年人教版九年级数学上册
《第13讲旋转中的最值路径长 讲义(学生版+教师版)2022年人教版九年级数学上册》由会员分享,可在线阅读,更多相关《第13讲旋转中的最值路径长 讲义(学生版+教师版)2022年人教版九年级数学上册(12页珍藏版)》请在七七文库上搜索。
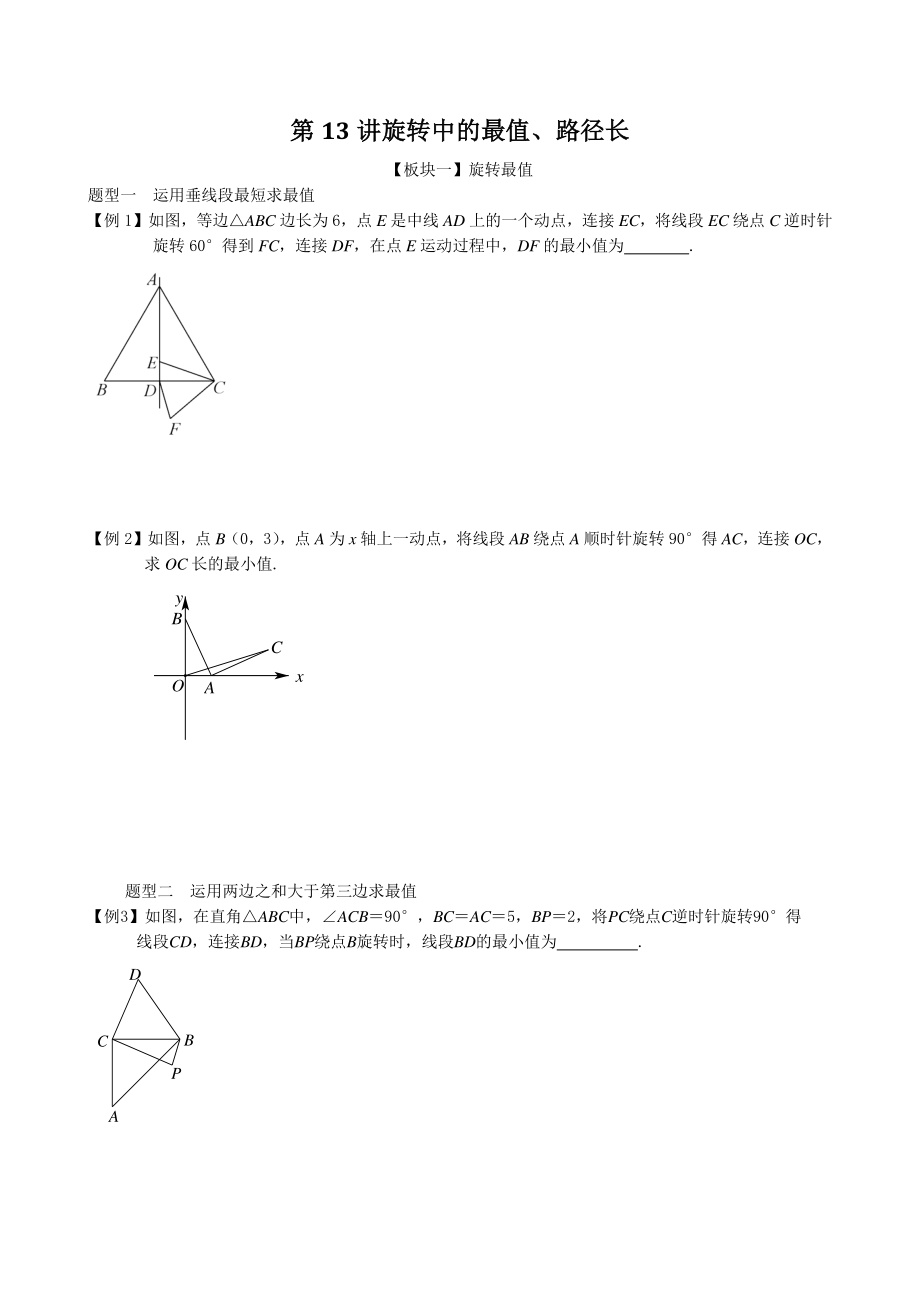
1、第第 13 讲旋转中的最值、路径长讲旋转中的最值、路径长 【板块一】旋转最值 题型一 运用垂线段最短求最值 【例 1】如图,等边ABC 边长为 6,点 E 是中线 AD 上的一个动点,连接 EC,将线段 EC 绕点 C 逆时针旋转 60得到 FC,连接 DF,在点 E 运动过程中,DF 的最小值为 . 【例 2】如图,点 B(0,3) ,点 A 为 x 轴上一动点,将线段 AB 绕点 A 顺时针旋转 90得 AC,连接 OC,求 OC 长的最小值. 题型二 运用两边之和大于第三边求最值 【例3】如图,在直角ABC中,ACB90,BCAC5,BP2,将PC绕点C逆时针旋转90得 线段CD,连接B
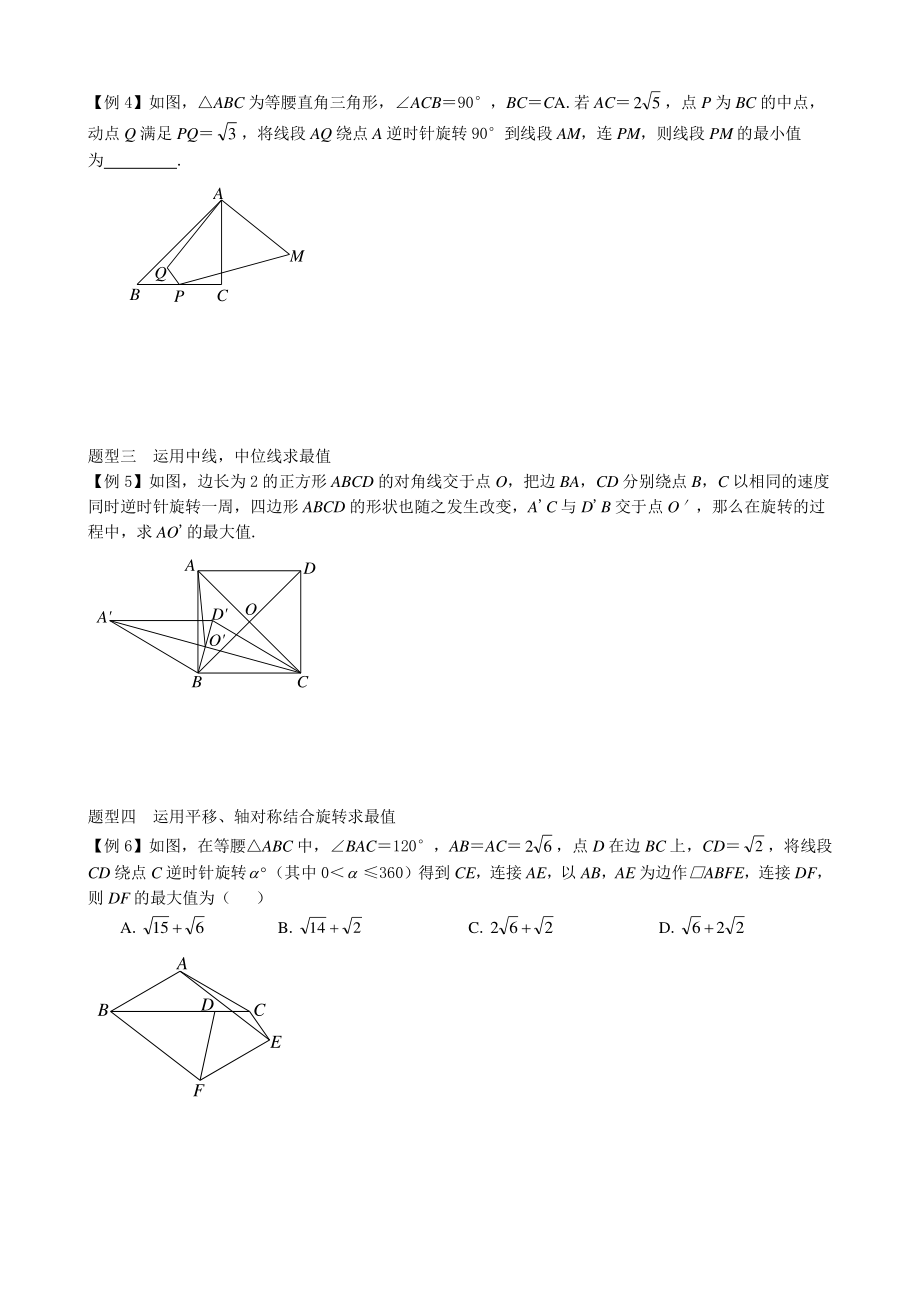
2、D,当BP绕点B旋转时,线段BD的最小值为 . BACxyOCABPD【例 4】如图,ABC 为等腰直角三角形,ACB90,BCCA.若 AC52,点 P 为 BC 的中点,动点 Q 满足 PQ3,将线段 AQ 绕点 A 逆时针旋转 90到线段 AM,连 PM,则线段 PM 的最小值为 . 题型三 运用中线,中位线求最值 【例 5】如图,边长为 2 的正方形 ABCD 的对角线交于点 O,把边 BA,CD 分别绕点 B,C 以相同的速度同时逆时针旋转一周,四边形 ABCD 的形状也随之发生改变,AC 与 DB 交于点 O,那么在旋转的过程中,求 AO的最大值. 题型四 运用平移、轴对称结合旋转
3、求最值 【例 6】如图,在等腰ABC 中,BAC120,ABAC62,点 D 在边 BC 上,CD2,将线段CD 绕点 C 逆时针旋转(其中 0360)得到 CE,连接 AE,以 AB,AE 为边作ABFE,连接 DF,则 DF 的最大值为( ) A.615 B.214 C.262 D.226 BCAMQPBADCODAOCADEBF针对练习 1 1.如图,在ABC 中,C90,BC6,AC10,D 为线段 AC 上一动点,将线段 BD 绕点 D 逆时针旋转 90.点 B 的对应点为点 E,连接 AE,求 AE 长的最小值. 2.如图,在平面直角坐标系中,点 A 的坐标为(2,0),点 B 的
4、坐标为(5,0),点 P 为线段 AB 外一动点,且 PA2,将 PB 绕点 P 逆时针旋转 90得 PM,求 AM 长的最大值. 3.如图,边长为4的正方形ABCD外有点E ,AEB90,F为DE的中点,连接CF.求CF的最大值. ACBDExAMBPyOFEDCBA【板块二】旋转图形中动点的路径与动线段的取值范围 题型一 旋转图形中点的运动路径 【例1】在平面直角坐标系中,点C沿某条路径运动,以点C为旋转中心,将点A(0,4)逆时针旋转90到点B(m,1),若5m5,求点C运动的路径长. 【例 2】如图,在平面直角坐标系中,直线 y13x1 分别交 x 轴,y 轴于点 B,点 A,点 M
5、为直线 AB 上一动点,连接 OM,将线段 OM 绕点 M 逆时针旋转 90,点 O 的对应点为点 N.当点 M 运动时,判断点 N的运动路线是什么图形,并说明理由. 题型二 旋转图形中变量的取值范围 【例3】在RtABC中,ACB90,ACBC,D,E分别在AC,BC上,DEAB,CFDE于点F,AC6,CF4,G是AE中点. (1)如图1,直接写出FG,BE的数量关系和位置关系为 ; (2)如图2,将CFE绕点C旋转,在旋转过程中,线段GF的取值范围是 . yxABCMNO-55yxNMBAO图1ABCDEFG图2ABCEFG 针对练习2 1.如图,矩形ABCD中,BC2AB8.点M,N分
6、别为AD,BC的中点,连接MN,点P是BC边上的动点,将PM绕点P顺时针方向旋转90得PE,当点P从点B运动到点C的过程中,点E运动的路径长为 . 2.如图,一副含30角和45角的三角板ABC和DEF叠E在一起,边BC与EF重合,BCEF12cm,点G为边BC(EF)的中点,边FD与AB相交于点H,将DEF绕点G按顺时针方向旋转,旋转角度从0到60的变化过程中,点H相应移动的路径长共为 . 3.如图,在RtABO中,BOA90,AO6,BO8,动点P从点A开始沿边AO向点O以每秒1个单位长度的速度运动,动点Q从点O开始沿边OB向点B以每秒2个单位长度的速度运动,连接PQ.点P,Q分别从点A,O
7、同时出发,当其中一点到达端点时,另一点也随之停止运动,在整个运动过程中,求出线段PQ的中点M所经过的路径长. NMPABCDEFHC(F)GDB(E)AGFEDCBAyxOMPQAB第第 13 讲讲 旋转中的最值、路径长旋转中的最值、路径长 【板块一】旋转最值 题型一 运用垂线段最短求最值 【例 1】如图,等边ABC 边长为 6,点 E 是中线 AD 上的一个动点,连接 EC,将线段 EC 绕点 C 逆时针旋转 60得到 FC,连接 DF,在点 E 运动过程中,DF 的最小值为 . 【解析】取 AC 的中点 G,连接 EG,在DCF 和GCE 中,CECF,DCFGCE, DCFGCE(SAS
8、),DFEG.根据垂线段最短,EGAD 时,EG 最短,即 DF 最短, 306021CAD,362121ACAG,EG 的最小值为5 . 132121AG, DF 的最小值为 1.5. 【例 2】如图,点 B(0,3) ,点 A 为 x 轴上一动点,将线段 AB 绕点 A 顺时针旋转 90得 AC,连接 OC,求 OC 长的最小值. 【解析】在 x 轴正半轴上取点 F,使 OFOB3,延长 CF 交 y 轴于点 D,在 OB 上截取 OEOA. 证AFCBEA. CFAAEB135,得点 C 在直线 DF 上运动,ODF 为等腰 直角三角形,当 OCDF 时 OC 最小为22323. 题型二
9、 运用两边之和大于第三边求最值 【例3】如图,在直角ABC中,ACB90,BCAC5,BP2,将PC绕点C逆时针旋转90得 线段CD,连接BD,当BP绕点B旋转时,线段BD的最小值为 . 【解析】连接 AP,DCBPCA(SAS) ,APBD,当点 P 在 AB 的延长线上时, BACEFDGBACxyOBACEFDxyOCABPDCABPDAP 的最大值ABPB252,BD 的最大值为225. 【例 4】如图,ABC 为等腰直角三角形,ACB90,BCCA.若 AC52,点 P 为 BC 的中点,动点 Q 满足 PQ3,将线段 AQ 绕点 A 逆时针旋转 90到线段 AM,连 PM,则线段

- 配套讲稿:
如PPT文件的首页显示word图标,表示该PPT已包含配套word讲稿。双击word图标可打开word文档。
- 特殊限制:
部分文档作品中含有的国旗、国徽等图片,仅作为作品整体效果示例展示,禁止商用。设计者仅对作品中独创性部分享有著作权。
- 关 键 词:
- 第13讲旋转中的最值路径长 讲义学生版+教师版2022年人教版九年级数学上册 13 旋转 中的 路径 讲义 学生 教师版 2022 年人教版 九年级 数学 上册
 七七文库所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
七七文库所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。



 浙公网安备33030202001339号
浙公网安备33030202001339号
链接地址:https://www.77wenku.com/p-219876.html