八年级数学暑假培优讲义：10：一元二次方程单元复习（教师版）

《八年级数学暑假培优讲义：10：一元二次方程单元复习（教师版）》由会员分享，可在线阅读，更多相关《八年级数学暑假培优讲义：10：一元二次方程单元复习（教师版）（11页珍藏版）》请在七七文库上搜索。

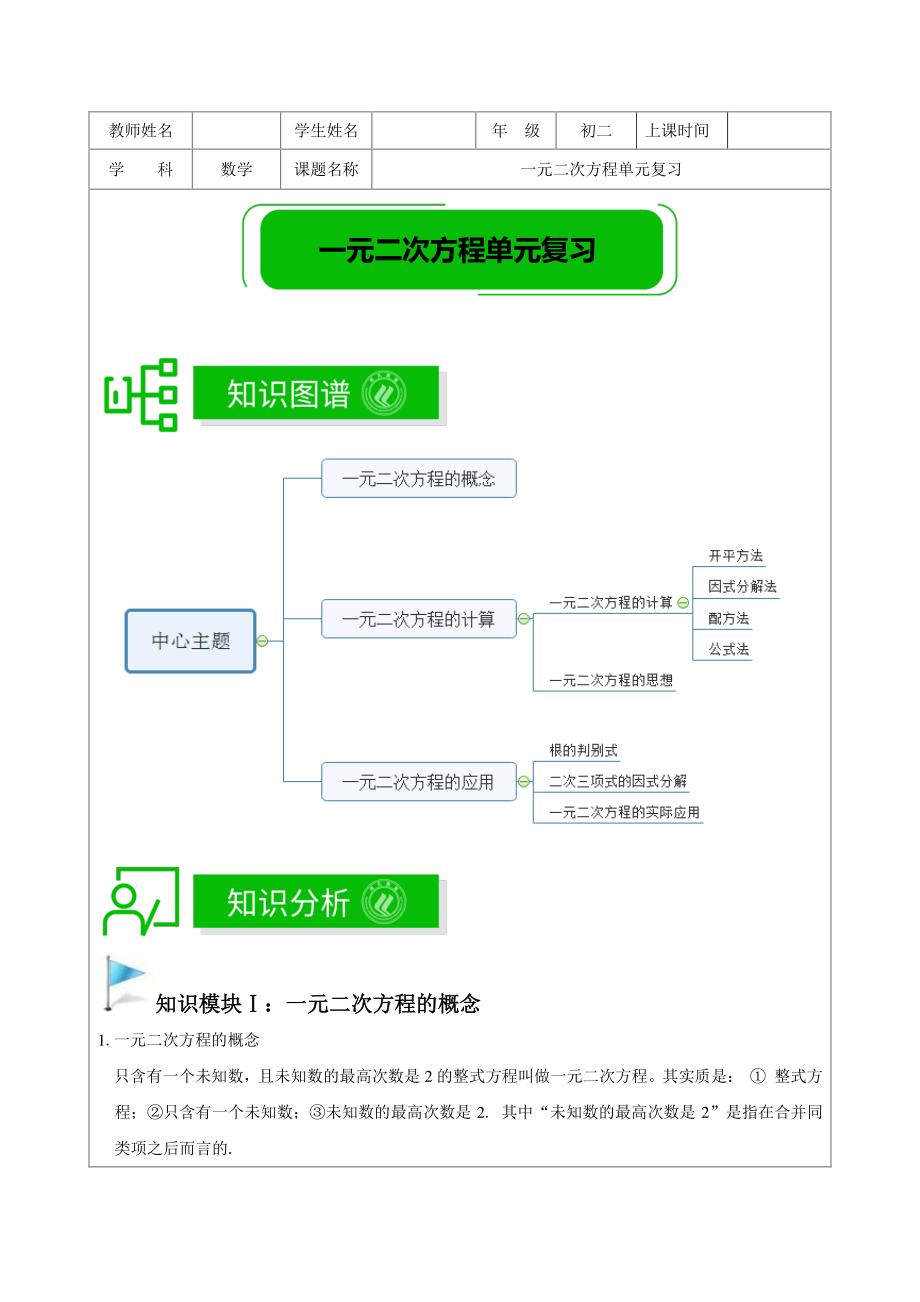
1、教师姓名 学生姓名 年 级 初二 上课时间 学 科 数学 课题名称 一元二次方程单元复习 知识模块：知识模块：一元二次方程的概念一元二次方程的概念 1.一元二次方程的概念 只含有一个未知数，且未知数的最高次数是 2 的整式方程叫做一元二次方程。其实质是： 整式方程；只含有一个未知数；未知数的最高次数是 2. 其中“未知数的最高次数是 2”是指在合并同类项之后而言的. 一元二次方程单元复习 2.一元二次方程的一般式 一元二次方程的一般式20(0)axbxca，其中2ax叫做二次项，a为二次项系数； bx叫做一次项，b是一次项系数；c叫做常数项。任何一个一元二次方程都可以化成一般形式. 3.二次项

2、系数含有字母的一元二次方程 二次项系数含有字母的方程是否是一元二次方程，需要对二次项系数进行讨论，要保证未 知数的最高次数 2，只需要二次项系数不为0 4对于一个一元二次方程，可以依据根的意义，判断未知数的一个值是不是这个方程的根. 5特殊根的一元二次方程的系数和常数项的特征 依据方程的根的意义，找出如果一元二次方程有一个根为0、1或1的一元二次方程的系 数和常数项的特征。如一元二次方程20axbxc(0)a ，当0c 时，有一根为0. 【例 1】下列关于x的方程：20axbxc；235a xa；2350 xx；235720 xx其中一元二次方程有（ ） A1 个 B2 个 C3 个 D4 个

3、 【答案】B 【例 2】若关于x的方程220 xxm的一根为 0，则m_ 【答案】0 知识模块：一元二次方程的计算知识模块：一元二次方程的计算 （一）（一）一元二次方程的解法一元二次方程的解法 1.开平方法 方程左边是喊未知数的完全平方式，右边是非负数常数形式，可用开平方法求解. 2.因式分解法 一元二次方程的一边是 0，另一边易于分解成两个一次因式时，就可以先考虑用因式分 解法求解. 3.配方法 为了能用开平方法解一般形式的一元二次方程20(0)axbcca，必须将方程形为 2()xmn的形式。配方法的步骤是：把二次项系数化为 1；移项，方程的一边为 二次项和一次项，另一边为常数项；方程两边

4、同时加上一次项系数一半的平方；将原 方程变形为2()xmn的形式. 4.公式法 一元二次方程20(0)axbcca求根公式242bbacxa 2(40)bac。它 对于任何一个一元二次方程都适用，其中也包括不完全的一元二次方程。如：256xx， 化成一般式2560 xx，得5,6,0abc 利用求根公式来求出方程的根. （二）（二）一元二次方程解法的运用及其思想方法一元二次方程解法的运用及其思想方法 配方法对所有的一元二次方程都适用，开平方法和因式法只对具备相应特征的方程才适 用.我们在解一元二次方程时一定要根据具体问题选择恰当的方法，从而使解题过程准确、 简捷.一般情况下： （1）形如20(

5、0)axcac的一元二次方程用开平方法或因式分解法（平方差公式）解； （2）形如20(0)axbxab的一元二次方程用因式分解法（提取公因式法）来解； （3）形如20(0)axbxcabc的一元二次方程用因式分解法（十字相乘法）来解. （4）公式法对所有的一元二次方程都适用，形如20(0)axbxcabc的一元二次方 程用因式分解法（十字相乘法）或公式法来解. 【例 3】 用适当的方法解一元二次方程 （1）09322 ）（ x （2）2(21)3(21)xx （3）23310 xx （4）112134x xxx 【答案】 （1）1230 xx（2）12112xx （3）121211212626

6、xx （4）1232xx 知识模块：一元二次方程的应用知识模块：一元二次方程的应用 （一）（一）根的判别式根的判别式 1.一元二次方程的根的判别式 我们把24bac叫做20(axbxca 的根的判别式，用符号来表示。对于一元 二次方程20(axbxca ，其根的情况与判别式的关系是： 当240bac 时，方程有两个不相等的实数根； 当240bac 时，方程有两个相等的实数根； 当240bac 时，方程没有实数根. 特别的：当240bac 时，方程有两个实数根. 上述判断反过来说，也是正确的。即 当方程有两个实数根时，240bac ； 当方程有两个相等的实数根时，240bac ； 当方程没有实数

7、根时，240bac ； 2.一元二次方程的根的判别式的应用 不解方程判别方程根的情况，即先把方程化为一般形式，然后求出判别式24bac 的值，最后根据的符号来确定根的情况； 根据一元二次方程根的情况确定方程中字母系数的取值范围，即先把方程化成一般形式 并求出它的判别式，然后根据根的情况列出判别式的方程或不等式，最后解这个不等式 或方程，但要去掉使方程二次项系数为零的字母的值。若问题中没有这个限制条件，就 要对二次项系数（含字母）是否为零进行讨论； 证明一元二次方程根的情况,可先把原方程化为一般形式,求出根的判别式,然后用配方 法或因式分解法确定判别式的符号,并由此得出结论. 3.利用根的判别式

8、解题时的几点注意 运用“”时必须把方程化为一般式; 不解方程判定方程的根的情况要由“；的符号判定； 运用判别式解题时，方程二次项系数一定不能为零； 【例 4】如果关于x的一元二次方程20 xxa 有两个不相等的实数根，那么a的取值范围 是_ 【答案】14a 【例 5】不解方程，判别方程2342xx的根的情况：_ 【答案】无实数根 【例 6】如果方程2610kxkx 有两个相等的实数根，则k的值是_ 【答案】19k 【例 7】下列关于x的方程中一定没有实数根的是（ ） A210 xx B24690 xx C2xx D220 xmx 【答案】B 【例 8】已知关于 x 的一元二次方程12) 1(2

9、xxm，求 （1）当m为何值时，方程有两个不相等的实数根； （2）当m为何值时，方程有两个相等的实数根； （3）当m为何值时，方程没有实数根。 【答案】 （1）21mm 且（2）2m（3）2m 【例 9】已知关于x的一元二次方程22230mxmxm有两个不相等的实数根 （1）求m的取值范围； （2）当m取满足条件的最大整数时，求方程的根 【答案】 （1）62mm且（2）12423xx （二）二次三项式的因式分解（二）二次三项式的因式分解 1二次三项式20axbxc a在实数范围内的因式分解公式 设12xx、是方程20axbxc a的两实根，则任何一个二次三项式2axbxc均可在实数范围内因式分

10、解为12a xxxx，即212axbxca xxxx 2二次三项式20axbxc a在实数范围内的分解因式 当240bac时，方程20axbxc a有两个不相等的实根12xx、， 20axbxc a可分解为12a xxxx； 当240bac时，方程20axbxc a有两个相等的实根， 20axbxc a可分解为一个完全平方式； 当240bac时，方程20axbxc a没有实根，20axbxc a在实 数范围内不能分解. 3二次三项式20axbxc a在实数范围内的因式分解的一般步骤 求出方程20axbxc a的两个实根12xx、； 写出分解式212axbxca xxxx，注意分解式中的因数a不

11、要漏写. 【例 10】下列多项式中，在实数范围不能分解因式的是（ ） A2222xyxy B2222xyxy C2244xyxy D2244xyy 【答案】A 【例 11】把二次三项式22285xxyy因式分解，下列结果中正确的是（ ） A464622xyxy B4646222xyxy C462462xyyxy D4646222xyxy 【答案】A 【例 12】 （1）.在实数范围内因式分解：243xx _ （2）.因式分解：222xxyy_ 【答案】 （1）2727xx（2）22yxyyxy 【例 13】写出一个整数m，使得二次三项式225xxm在实数范围内能分解因式符合条件的整数m可以是：

12、_ 【答案】3的任意整数 （三）一元二次方程的实际应用（三）一元二次方程的实际应用 1一元二次方程的应用的常见类型 与面积相关的几何问题。如：有长比宽多 20 米的矩形菜园一块，它的四周有宽 1 米的 道路。已知道路的面积是 164 平方米，求此菜园的面积。可设菜园宽为x米，则长为 20 x米，列方程，得22220164xxx x 有关增长率的问题。如：某工厂七月份生产值为 100 万元，计划八、九两月的产值要 达到 114 万元，如果每月增长率相同，求这个增长率。可设平均每月的增长率为x， 列出方程：2100 1144x 有关销售问题。如：某商场按标价销售某种工艺品时，按标价出售，每件可获利

13、 45 元，并且商场每天可售出该工艺品 100 件，若每件工艺品降价 1 元，则每天可多售出 该工艺品 4 件，问每件工艺品降价多少元出售，每天可获得的利润为 4900 元？可设每件工艺品降价x元出售，列出方程：4510044900 xx 2列方程解应用题的几点注意 首先要多角度、全方位地理解题意，对关键词要细心揣摩，并注意发现题目中的隐含 条件； 选择适当未知数，列出方程； 要抓住各类题型中的“基本量“及所具有的等量关系，并熟悉它们的变形。如 销售问题中某商品的价格上涨或下降，引起销售量的变化（倍数关系） ；增长率问题： 增长率=或增长率= 【例 14】如图，某小区规划在一个长 40 米，宽

14、为 26 米的矩形场地 ABCD 上，修建三条同样宽 的道路，使其中两条与 AB 平行，另一条与 AD 平行，其余部分种草，若使每块草坪的面积都为 144 平方米，求道路的宽度 【答案】2 米 【例 15】某商场将每件进价为 80 元的某种商品原来按每件 100 元出售，每天可售出 100 件，为 了扩大销售，增加盈利，尽快减少库存，商场决定采取适当的降价措施，经过市场调查， 发现这种商品售价每降低 1 元，商场销量平均每天可增加 10 件 （1）假设销售单价降低 x 元，那么销售每件这种商品所获得的利润是_元；这种商品每天的销售量是_件（用含 x 的代数式表示） ； （2）若商场经营该商品一

15、天要获利润 2160 元，则每件商品应降价多少元？ 【答案】 （1）20100 10 xx（2）8 元 【习题 1】下列方程中，是一元二次方程的是（ ） A25xy B230 xx C231xxx x D210 xx 增长数计划数增长数原产量【答案】B 【习题 2】 如果关于x的一元二次方程2210 xxm 有两个不相等的实数根， 那么x的取值范围是（ ） A2m B2m C2m且1m D2m且1m 【答案】B 【习题 3】下列关于 x 的方程中一定有实数解的是（ ） A210 xx B2240 xx C220 xxm D210 xmxm 【答案】D 【习题 4】在实数范围内分解因式：224x

16、x _ 【答案】1515xx 【习题 5】如图，在一块长 92m、宽 60m 的矩形耕地上挖三条水渠（水渠的宽都相等） ，水渠把耕地 分成面积均为 885m2的 6 个矩形小块，水渠应挖多宽？设水渠应挖宽为x，根据题意，可列方程：_ 【答案】92260885 6xx 【习题 6】用适当的方法解方程。 （1）02522 ）（x （2）025)2(10)2(2xx （3） 26180 xx （4）22742xx-= 【答案】 （1）1237xx （2）1233xx（3）123 3 33 3 3xx （4）1222 522 5xx 【习题 7】求证：不论k为何值，关于x的方程03) 12(2kxkx

17、总有两个不相等的实数根。 【答案】省略 【习题 8】若关于x的一元二次方程2230 xaxab的根的判别式的值等于 0，且 2 是这个方程的一个根，求 a、b 的值。 【答案】22ab 【习题 9】已知 a，b，c 是ABC 的三边，判断方程220cxab xc的根的情况 【答案】无实数根 【习题 10】某地区环保局在检查该地区某铝厂时发现，该厂污水严重影响周围环境，要求作定期整 改，据估测，该厂年排放污水量为 50 万吨，接到通知后，该厂决定分两期投入治理，一 方面对排放的污水进行处理，同时使得处理后的污水年排放量减少到 40.5 万吨，如果每 期治理中污水减少的百分率相同 （1）求每期减少

18、的百分率为多少？ （2）如果第一期治理中每减少排放 1 万吨污水，需投入 2 万元，第二期每减少排放 1 万 吨污水，需投入 3 万元，问预计两期治理共需多少万元？ 【答案】 （1）10%（2）23.5 万元 【习题 11】商场某种新商品每件进价是 120 元，在试销期间发现，当每件商品售价为 130 元时，每 天可销售 70 件，当每件商品售价高于 130 元时，每涨价 1 元，日销售量就减少 1 件据 此规律，请回答： （1）当每件商品售价定为 170 元时，每天可销售多少件商品，商场获得的日盈利是多少？ （2）在上述条件不变，商品销售正常的情况下，每件商品的销售价定为多少元时，商场 日盈利可达到 1600 元？（提示：盈利=售价进价） 【答案】 （1）30 件 1500 元（2）160 元