2023年湖北省随州市中考数学试卷（含答案解析）

《2023年湖北省随州市中考数学试卷（含答案解析）》由会员分享，可在线阅读，更多相关《2023年湖北省随州市中考数学试卷（含答案解析）（33页珍藏版）》请在七七文库上搜索。

1、2023年湖北省随州市中考数学试题一、选择题（本大题共10小题，每小题3分，共30分）1. 实数2023的绝对值是（）A. 2023B. 2023C. D. 2. 如图，直线，直线l与、相交，若图中，则为（ ） A. B. C. D. 3. 如图是一个放在水平桌面上的圆柱体，该几何体的三视图中完全相同的是（ ） A. 主视图和俯视图B. 左视图和俯视图C. 主视图和左视图D. 三个视图均相同4. 某班在开展劳动教育课程调查中发现，第一小组6名同学每周做家务的天数依次为3，7，5，6，5，4（单位：天），则这组数据的众数和中位数分别为（ ）A. 5和5B. 5和4C. 5和6D. 6和55. 甲

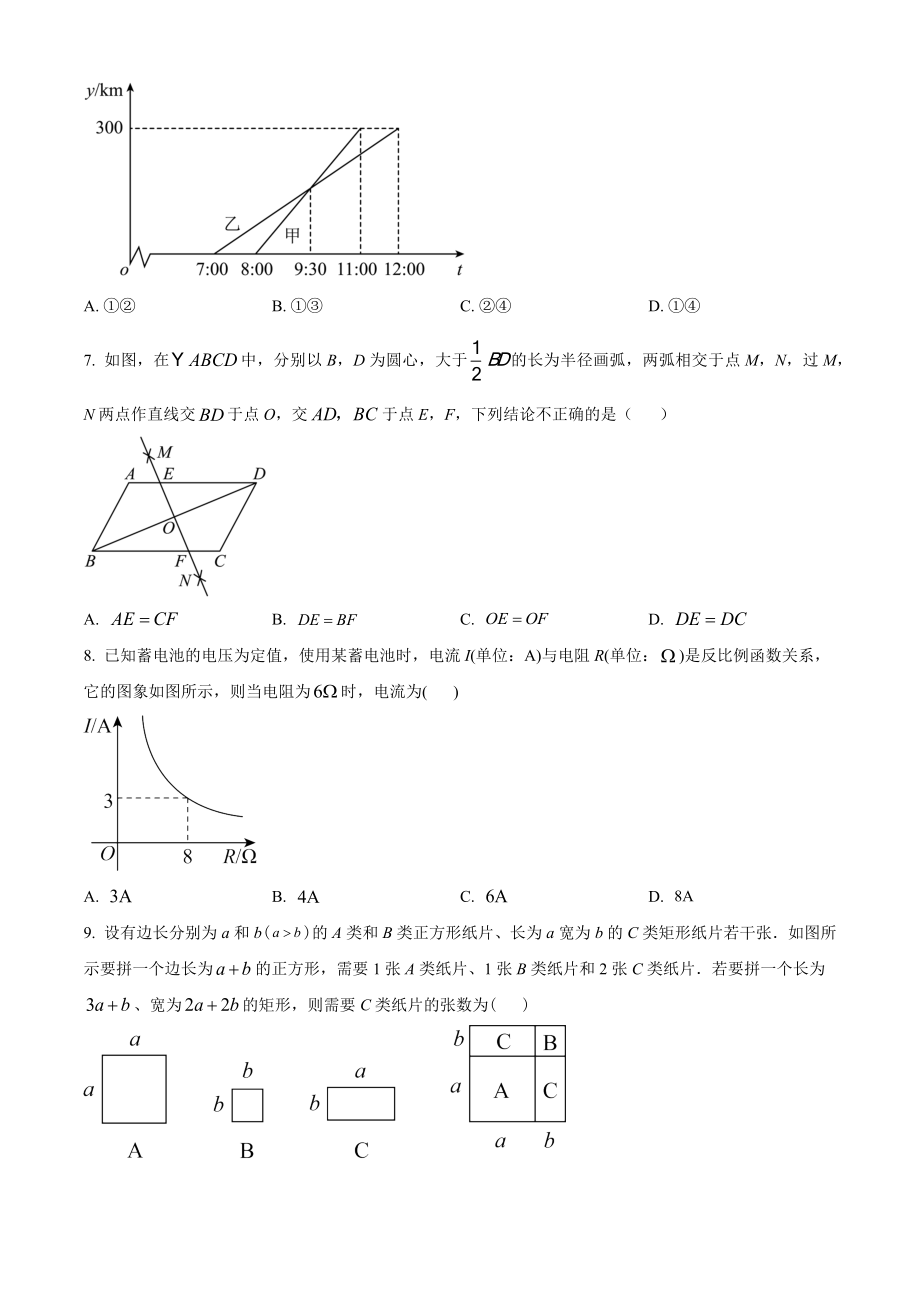
2、、乙两个工程队共同修一条道路，其中甲工程队需要修9千米，乙工程队需要修12千米已知乙工程队每个月比甲工程队多修1千米，最终用的时间比甲工程队少半个月若设甲工程队每个月修x千米，则可列出方程为（ ）A. B. C. D. 6. 甲、乙两车沿同一路线从A城出发前往B城，在整个行程中，汽车离开A城的距离y与时刻t的对应关系如图所示，关于下列结论：A，B两城相距；甲车的平均速度是，乙车的平均速度是；乙车先出发，先到达B城；甲车在追上乙车正确的有（ ） A. B. C. D. 7. 如图，在中，分别以B，D为圆心，大于的长为半径画弧，两弧相交于点M，N，过M，N两点作直线交于点O，交于点E，F，下列结论

3、不正确的是（ ） A. B. C. D. 8. 已知蓄电池的电压为定值，使用某蓄电池时，电流I(单位：A)与电阻R(单位：)是反比例函数关系，它的图象如图所示，则当电阻为时，电流为( ) A. B. C. D. 9. 设有边长分别为a和b()的A类和B类正方形纸片、长为a宽为b的C类矩形纸片若干张如图所示要拼一个边长为的正方形，需要1张A类纸片、1张B类纸片和2张C类纸片若要拼一个长为、宽为的矩形，则需要C类纸片的张数为( ) A. 6B. 7C. 8D. 910. 如图，已知开口向下抛物线与x轴交于点，对称轴为直线则下列结论正确的有（ ）；方程的两个根为；抛物线上有两点和，若且，则 A. 1

4、个B. 2个C. 3个D. 4个二、填空题（本大题共有6小题，每小题3分，共18分只需要将结果直接填写在答题卡对应题号处的横线上）11. 计算：_12. 如图，在中，则的度数为_ 13. 已知一元二次方程x23x10有两个实数根x1，x2，则x1x2x1x2的值等于_14. 如图，在中，D为上一点，若是的角平分线，则_ 15. 某天老师给同学们出了一道趣味数学题：设有编号为1-100的100盏灯，分别对应着编号为1-100的100个开关，灯分为“亮”和“不亮”两种状态，每按一次开关改变一次相对应编号的灯的状态，所有灯的初始状态为“不亮”现有100个人，第1个人把所有编号是1的整数倍的开关按一次

5、，第2个人把所有编号是2的整数倍的开关按一次，第3个人把所有编号是3的整数倍的开关按一次，第100个人把所有编号是100的整数倍的开关按一次问最终状态为“亮”的灯共有多少盏？几位同学对该问题展开了讨论：甲：应分析每个开关被按的次数找出规律：乙：1号开关只被第1个人按了1次，2号开关被第1个人和第2个人共按了2次，3号开关被第1个人和第3个人共按了2次，丙：只有按了奇数次的开关所对应的灯最终是“亮”的状态根据以上同学的思维过程，可以得出最终状态为“亮”的灯共有_盏16. 如图，在矩形中，M是边上一动点（不含端点），将沿直线对折，得到当射线交线段于点P时，连接，则面积为_；的最大值为_ 三、解答题

6、（本大题共8小题，共72分解答应写出必要的演算步骤、文字说明或证明过程）17. 先化简，再求值：，其中18. 如图，矩形的对角线，相交于点O， （1）求证：四边形是菱形；（2）若，求四边形的面积19. 中学生心理健康受到社会的广泛关注，某校开展心理健康教育专题讲座，就学生对心理健康知识的了解程度，采用随机抽样调查的方式，根据收集到的信息进行统计，绘制了下面两幅尚不完整的统计图 根据图中信息回答下列问题：（1）接受问卷调查的学生共有_人，条形统计图中m的值为_，扇形统计图中“非常了解”部分所对应扇形的圆心角的度数为_；（2）若该校共有学生800人，根据上述调查结果，可以估计出该校学生中对心理健康

7、知识“不了解”的总人数为_人；（3）若某班要从对心理健康知识达到“非常了解”程度的2名男生和2名女生中随机抽取2人参加心理健康知识竞赛，请用列表或画树状图的方法，求恰好抽到2名女生的概率20. 某校学生开展综合实践活动，测量某建筑物的高度，在建筑物附近有一斜坡，坡长米，坡角，小华在C处测得建筑物顶端A的仰角为，在D处测得建筑物顶端A的仰角为（已知点A，B，C，D在同一平面内，B，C在同一水平线上） （1）求点D到地面的距离；（2）求该建筑物的高度21. 如图，是的直径，点E，C在上，点C是的中点，垂直于过C点的直线，垂足为D，的延长线交直线于点F （1）求证：是的切线；（2）若，求的半径；求线

8、段的长22. 为了振兴乡村经济，增加村民收入，某村委会干部带领村民在网上直播推销农产品，在试销售的30天中，第x天（且x为整数）的售价p（元/千克）与x的函数关系式（且x为整数），销量q（千克）与x的函数关系式为，已知第5天售价为50元/千克，第10天售价为40元/千克，设第x天的销售额为W元（1）_， _；（2）求第x天的销售额W元与x之间的函数关系式；（3）在试销售的30天中，销售额超过1000元的共有多少天？23. 1643年，法国数学家费马曾提出一个著名的几何问题：给定不在同一条直线上的三个点A，B，C，求平面上到这三个点的距离之和最小的点的位置，意大利数学家和物理学家托里拆利给出了分

9、析和证明，该点也被称为“费马点”或“托里拆利点”，该问题也被称为“将军巡营”问题（1）下面是该问题的一种常见的解决方法，请补充以下推理过程：（其中处从“直角”和“等边”中选择填空，处从“两点之间线段最短”和“三角形两边之和大于第三边”中选择填空，处填写角度数，处填写该三角形的某个顶点）当的三个内角均小于时，如图1，将绕，点C顺时针旋转得到，连接， 由，可知 三角形，故，又，故，由 可知，当B，P，A在同一条直线上时，取最小值，如图2，最小值为，此时的P点为该三角形的“费马点”，且有 ；已知当有一个内角大于或等于时，“费马点”为该三角形的某个顶点如图3，若，则该三角形的“费马点”为 点（2）如图

10、4，在中，三个内角均小于，且，已知点P为“费马点”，求的值； （3）如图5，设村庄A，B，C连线构成一个三角形，且已知现欲建一中转站P沿直线向A，B，C三个村庄铺设电缆，已知由中转站P到村庄A，B，C的铺设成本分别为a元/，a元/，元/，选取合适的P的位置，可以使总的铺设成本最低为_元（结果用含a的式子表示）24. 如图1，平面直角坐标系中，抛物线过点，和，连接，点为抛物线上一动点，过点作轴交直线于点，交轴于点 （1）直接写出抛物线和直线的解析式；（2）如图2，连接，当为等腰三角形时，求的值；（3）当点在运动过程中，在轴上是否存在点，使得以，为顶点的三角形与以，为顶点的三角形相似（其中点与点相

11、对应），若存在，直接写出点和点的坐标；若不存在，请说明理由2023年湖北省随州市中考数学试题一、选择题（本大题共10小题，每小题3分，共30分）1. 实数2023的绝对值是（）A. 2023B. 2023C. D. 【答案】A【解析】【分析】根据绝对值的代数意义即可得出答案【详解】解：因为负数的绝对值等于它的相反数，所以，2023的绝对值等于2023故选：A【点睛】本题考查了绝对值的代数意义，熟练掌握知识点是本题的关键2. 如图，直线，直线l与、相交，若图中，则为（ ） A. B. C. D. 【答案】C【解析】【分析】根据两直线平行，同旁内角互补进行求解，即可得到答案【详解】解：直线，故选C

12、【点睛】本题考查了平行线的性质，解题关键是掌握两直线平行，同位角相等，内错角相等，同旁内角互补3. 如图是一个放在水平桌面上的圆柱体，该几何体的三视图中完全相同的是（ ） A. 主视图和俯视图B. 左视图和俯视图C. 主视图和左视图D. 三个视图均相同【答案】C【解析】【分析】根据三视图的定义判断即可【详解】该几何体的三视图中完全相同的是主视图和左视图，均为矩形，俯视图是一个圆故选：C【点睛】本题考查三视图的知识点，主要掌握主视图、左视图、俯视图分别是从物体的前面、左面、上面看到的图形是解题的关键4. 某班在开展劳动教育课程调查中发现，第一小组6名同学每周做家务的天数依次为3，7，5，6，5，

13、4（单位：天），则这组数据的众数和中位数分别为（ ）A. 5和5B. 5和4C. 5和6D. 6和5【答案】A【解析】【分析】根据众数和中位数的概念求解【详解】解：将数据重新排列为3，4，5，5，6，7，所以这组数据的众数为5，中位数，故选：A【点睛】本题考查了众数和中位数的概念：一组数据中出现次数最多的数据叫做众数；将一组数据按照从小到大（或从大到小）的顺序排列，如果数据的个数是奇数，则处于中间位置的数就是这组数据的中位数；如果这组数据的个数是偶数，则中间两个数据的平均数就是这组数据的中位数5. 甲、乙两个工程队共同修一条道路，其中甲工程队需要修9千米，乙工程队需要修12千米已知乙工程队每个

14、月比甲工程队多修1千米，最终用的时间比甲工程队少半个月若设甲工程队每个月修x千米，则可列出方程为（ ）A. B. C. D. 【答案】A【解析】【分析】设甲工程队每个月修x千米，则乙工程队每个月修千米，根据“最终用的时间比甲工程队少半个月”列出分式方程即可【详解】解：设甲工程队每个月修x千米，则乙工程队每个月修千米，依题意得，故选：A【点睛】此题主要考查了由实际问题抽象出分式方程，关键是分析题意，找准关键语句，列出相等关系6. 甲、乙两车沿同一路线从A城出发前往B城，在整个行程中，汽车离开A城的距离y与时刻t的对应关系如图所示，关于下列结论：A，B两城相距；甲车的平均速度是，乙车的平均速度是；

15、乙车先出发，先到达B城；甲车在追上乙车正确的有（ ） A. B. C. D. 【答案】D【解析】【分析】根据图象逐项分析判断即可【详解】解：由图象知：A，B两城相距，故此项正确；甲车的平均速度是，乙车的平均速度是，故此项错误；乙车先出发，才到达B城，甲车后出发，就到达B城，故此项错误；两车在时，行驶路程一样，即甲车在追上乙车，故此项正确综上，说法正确，故选：D【点睛】本题考查了函数的图象，正确识别图象并能提取相关信息是解答的关键7. 如图，在中，分别以B，D为圆心，大于的长为半径画弧，两弧相交于点M，N，过M，N两点作直线交于点O，交于点E，F，下列结论不正确的是（ ） A. B. C. D.

16、 【答案】D【解析】【分析】根据作图可知：垂直平分，得到，于是得到点O为的对称中心，根据全等三角形的性质得到，根据平行线的性质得到，推出四边形是菱形，据此判断即可【详解】解：根据作图可知：垂直平分，点O为的对称中心， ，在中，故B正确；，故A正确；四边形是菱形，故C正确；与不一定相等，故D错误，故选：D【点睛】本题考查了垂直平分线的性质，尺规作图，菱形的判定与性质，全等三角形的判定与性质等知识，掌握菱形的判定与性质是解答本题的关键8. 已知蓄电池的电压为定值，使用某蓄电池时，电流I(单位：A)与电阻R(单位：)是反比例函数关系，它的图象如图所示，则当电阻为时，电流为( ) A. B. C. D

17、. 【答案】B【解析】【分析】设该反比函数解析式为，根据当时，可得该反比函数解析式为，再把代入，即可求出电流I【详解】解：设该反比函数解析式为，由题意可知，当时，解得：，设该反比函数解析式为，当时，即电流为，故选：B【点睛】本题考查了反比例函数的图象和性质，求出反比例函数解析式是解题关键9. 设有边长分别为a和b()的A类和B类正方形纸片、长为a宽为b的C类矩形纸片若干张如图所示要拼一个边长为的正方形，需要1张A类纸片、1张B类纸片和2张C类纸片若要拼一个长为、宽为的矩形，则需要C类纸片的张数为( ) A. 6B. 7C. 8D. 9【答案】C【解析】【分析】计算出长为，宽为的大长方形的面积，

18、再分别得出A、B、C卡片的面积，即可看出应当需要各类卡片多少张【详解】解：长为，宽为的大长方形的面积为：；需要6张A卡片，2张B卡片和8张C卡片故选：C【点睛】本题主要考查多项式乘多项式与图形面积，解题的关键是理解结果中项的系数即为需要C类卡片的张数10. 如图，已知开口向下的抛物线与x轴交于点，对称轴为直线则下列结论正确的有（ ）；方程的两个根为；抛物线上有两点和，若且，则 A. 1个B. 2个C. 3个D. 4个【答案】B【解析】【分析】根据抛物线的图象与系数的关系即可求出答案【详解】解：由抛物线的开口可知：，由抛物线与y轴的交点可知：，由抛物线的对称轴可知：，故正确；抛物线与x轴交于点，

19、对称轴为直线，则另一个交点，时，故正确；抛物线与x轴交于点和，的两根为6和，则，如果方程的两个根为成立，则，而，方程的两个根为不成立，故不正确；，P、Q两点分布在对称轴的两侧，即到对称轴的距离小于到对称轴的距离，故不正确综上，正确的有，故选：B【点睛】本题考查的是二次函数图象与系数的关系，二次函数系数符号由抛物线开口方向、对称轴、抛物线与y轴的交点抛物线与x轴交点的个数确定二、填空题（本大题共有6小题，每小题3分，共18分只需要将结果直接填写在答题卡对应题号处的横线上）11. 计算：_【答案】0【解析】分析】先算乘方，再计算乘法，最后算加减【详解】解：故答案为：0【点睛】此题主要考查了有理数的

20、混合运算，关键是掌握运算法则12. 如图，在中，则的度数为_ 【答案】#30度【解析】【分析】根据垂径定理得到，根据圆周角定理解答即可【详解】解：，故答案为：【点睛】本题考查的是垂径定理和圆周角定理，掌握同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半是解题的关键13. 已知一元二次方程x23x10有两个实数根x1，x2，则x1x2x1x2的值等于_【答案】2【解析】【分析】先根据根与系数的关系得x1+x23，x1x21，然后利用整体代入的方法计算【详解】解：根据根与系数的关系得：x1+x23，x1x21，x1+x2x1x2312故答案为：2【点睛】本题考查了根与系数的关系：若x1，

21、x2是一元二次方程ax2+bx+c0（a0）的两根时，x1+x2，x1x2熟练掌握根与系数的关系是解决本题的关键14. 如图，在中，D为上一点，若是的角平分线，则_ 【答案】3【解析】【分析】首先证明，设，在中，利用勾股定理构建方程即可解决问题【详解】解：如图，过点D作的垂线，垂足为P， 在中，是的角平分线，设，在中，故答案为：3【点睛】本题考查了角平分线的性质，全等三角形的判定和性质，勾股定理等知识，解题的关键是熟练掌握基本知识，属于中考常考题型15. 某天老师给同学们出了一道趣味数学题：设有编号为1-100100盏灯，分别对应着编号为1-100的100个开关，灯分为“亮”和“不亮”两种状态

22、，每按一次开关改变一次相对应编号的灯的状态，所有灯的初始状态为“不亮”现有100个人，第1个人把所有编号是1的整数倍的开关按一次，第2个人把所有编号是2的整数倍的开关按一次，第3个人把所有编号是3的整数倍的开关按一次，第100个人把所有编号是100的整数倍的开关按一次问最终状态为“亮”的灯共有多少盏？几位同学对该问题展开了讨论：甲：应分析每个开关被按的次数找出规律：乙：1号开关只被第1个人按了1次，2号开关被第1个人和第2个人共按了2次，3号开关被第1个人和第3个人共按了2次，丙：只有按了奇数次的开关所对应的灯最终是“亮”的状态根据以上同学的思维过程，可以得出最终状态为“亮”的灯共有_盏【答案

23、】10【解析】【分析】灯的初始状态为“不亮”，按奇数次，则状态为“亮”，按偶数次，则状态为“不亮”，确定1-100中，各个数因数的个数，完全平方数的因数为奇数个，从而求解【详解】所有灯的初始状态为“不亮”，按奇数次，则状态为“亮”，按偶数次，则状态为“不亮”；因数的个数为奇数的自然数只有完全平方数，1-100中，完全平方数为1，4，9，16，25，36，49，64，81，100；有10个数，故有10盏灯被按奇数次，为“亮”的状态；故答案为：10【点睛】本题考查因数分解，完全平方数，理解因数的意义，完全平方数的概念是解题的关键16. 如图，在矩形中，M是边上一动点（不含端点），将沿直线对折，得到

24、当射线交线段于点P时，连接，则的面积为_；的最大值为_ 【答案】 . . 【解析】【分析】（1）根据等底等高的三角形和矩形面积关系分析求解；（2）结合勾股定理分析可得，当最大时，即最大，通过分析点N的运动轨迹，结合勾股定理确定的最值，从而求得的最大值【详解】解：由题意可得的面积等于矩形的一半，的面积为，在中，当最大时，即最大，由题意可得点N是在以D为圆心4为半径的圆上运动，当射线与圆相切时，最大，此时C、N、M三点共线，如图： 由题意可得：，在中，故答案为：，【点睛】本题考查了矩形的性质、折叠的性质、全等三角形的判定与性质、勾股定理等知识；本题综合性强，难度较大，熟练掌握矩形和折叠的性质，分析

25、点的运动轨迹，证明三角形全等是解决问题的关键三、解答题（本大题共8小题，共72分解答应写出必要的演算步骤、文字说明或证明过程）17. 先化简，再求值：，其中【答案】，【解析】【分析】先根据分式的减法法则算括号里面的，再根据分式的除法法则把除法变成乘法，算乘法，最后代入求出答案即可【详解】解：，当时，原式【点睛】本题考查了分式的化简求值，能正确根据分式的运算法则进行化简是解此题的关键，注意运算顺序18. 如图，矩形的对角线，相交于点O， （1）求证：四边形是菱形；（2）若，求四边形的面积【答案】（1）见解析 （2）3【解析】【分析】（1）先根据矩形的性质求得，然后根据有一组邻边相等的平行四边形是

26、菱形分析推理；（2）根据矩形的性质求得的面积，然后结合菱形的性质求解【小问1详解】解：，四边形是平行四边形，又矩形中，平行四边形是菱形；【小问2详解】解：矩形的面积为，的面积为，菱形的面积为【点睛】本题考查矩形的性质、菱形的判定，属于中考基础题，掌握矩形的性质和菱形的判定方法，正确推理论证是解题关键19. 中学生心理健康受到社会的广泛关注，某校开展心理健康教育专题讲座，就学生对心理健康知识的了解程度，采用随机抽样调查的方式，根据收集到的信息进行统计，绘制了下面两幅尚不完整的统计图 根据图中信息回答下列问题：（1）接受问卷调查的学生共有_人，条形统计图中m的值为_，扇形统计图中“非常了解”部分所

27、对应扇形的圆心角的度数为_；（2）若该校共有学生800人，根据上述调查结果，可以估计出该校学生中对心理健康知识“不了解”的总人数为_人；（3）若某班要从对心理健康知识达到“非常了解”程度的2名男生和2名女生中随机抽取2人参加心理健康知识竞赛，请用列表或画树状图的方法，求恰好抽到2名女生的概率【答案】（1）80，16， （2）40 （3）恰好抽到2名女生的概率为【解析】【分析】（1）用“基本了解”的人数除以它所占的百分比得到调查的总人数，再用总人数减去其他项的人数，求出“了解很少”的人数；用乘以扇形统计图中“非常了解”部分所占的比例即可；（2）用总人数800乘以“不了解”的人数所占的比例即可；（

28、3）画树状图展示所有12种等可能的结果数，找出恰好抽到2名女生的结果数，然后利用概率公式求解【小问1详解】解：接受问卷调查的学生共有（人，（人，扇形统计图中“非常了解”部分所对应扇形的圆心角的度数为；故答案为：80，16，；【小问2详解】解：根据题意得：（人，答：估计出该校学生中对心理健康知识“不了解”的总人数为40人；故答案为：40；【小问3详解】解：由题意列树状图： 由树状图可知，所有等可能的结果有12种，恰好抽到2名女生的结果有2种，恰好抽到2名女生的概率为【点睛】此题考查了列表法或树状图法求概率以及条形统计图与扇形统计图用到的知识点为：概率=所求情况数与总情况数之比20. 某校学生开展

29、综合实践活动，测量某建筑物的高度，在建筑物附近有一斜坡，坡长米，坡角，小华在C处测得建筑物顶端A的仰角为，在D处测得建筑物顶端A的仰角为（已知点A，B，C，D在同一平面内，B，C在同一水平线上） （1）求点D到地面的距离；（2）求该建筑物的高度【答案】（1）5米 （2）米【解析】【分析】（1）过点D作，根据坡角的概念及含直角三角形的性质分析求解；（2）通过证明，然后解直角三角形分析求解【小问1详解】解：过点D作， 由题意可得，在Rt中，即点D到地面的距离为5米；【小问2详解】如图， 由题意可得，又，在Rt中，即，解得，在Rt中，即，解得，答：该建筑物的高度为15米【点睛】本题考查的是解直角三角

30、形的应用-仰角俯角、坡度坡角问题，根据题意作出辅助线，构造出直角三角形是解答此题的关键21. 如图，是的直径，点E，C在上，点C是的中点，垂直于过C点的直线，垂足为D，的延长线交直线于点F （1）求证：是的切线；（2）若，求的半径；求线段的长【答案】（1）证明见解析 （2）3；2【解析】【分析】（1）根据等弧所对的圆周角相等和等边对等角的性质，得到，推出，进而得到，再利用圆的切线的判定定理即可证明结论；（2）连接，根据直径所对的圆周角是直角和平行线的判定，得到，进而得到，再利用锐角三角函数，求得，即可求出的半径；利用锐角三角函数，分别求出和的长，即可得到线段的长【小问1详解】证明：如图，连接，

31、 点C是的中点，是的半径，是的切线；【小问2详解】解：如图，连接， 是直径，的半径为；由（1）可知，【点睛】本题是圆和三角形综合题，考查了圆的切线的判定定理，圆的性质，等腰三角形的性质，锐角三角函数等知识，熟练掌握圆的相关性质，灵活运用正弦值求边长是解题关键22. 为了振兴乡村经济，增加村民收入，某村委会干部带领村民在网上直播推销农产品，在试销售的30天中，第x天（且x为整数）的售价p（元/千克）与x的函数关系式（且x为整数），销量q（千克）与x的函数关系式为，已知第5天售价为50元/千克，第10天售价为40元/千克，设第x天的销售额为W元（1）_， _；（2）求第x天的销售额W元与x之间的函

32、数关系式；（3）在试销售的30天中，销售额超过1000元的共有多少天？【答案】（1）， （2）时，当时， （3）7天【解析】【分析】（1）利用待定系数法求待定系数；（2）根据“销售额=售价销售量”列出函数关系式，（3）利用二次函数和一次函数的性质分析求解.【小问1详解】解：第5天售价为50元/千克，第10天售价为40元/千克，解得，故答案为：，；【小问2详解】解：由题意当时，当时，【小问3详解】解：由题意当时，当时，最大为，当时，由时，解得，又x为整数，且，当时，随的增大而增大，第至天，销售额超过1000元，共7天【点睛】本题考查一次函数的应用，二次函数的应用，理解题意，分段分析函数解析式，掌

33、握一次函数和二次函数的性质是解题关键23. 1643年，法国数学家费马曾提出一个著名的几何问题：给定不在同一条直线上的三个点A，B，C，求平面上到这三个点的距离之和最小的点的位置，意大利数学家和物理学家托里拆利给出了分析和证明，该点也被称为“费马点”或“托里拆利点”，该问题也被称为“将军巡营”问题（1）下面是该问题的一种常见的解决方法，请补充以下推理过程：（其中处从“直角”和“等边”中选择填空，处从“两点之间线段最短”和“三角形两边之和大于第三边”中选择填空，处填写角度数，处填写该三角形的某个顶点）当的三个内角均小于时，如图1，将绕，点C顺时针旋转得到，连接， 由，可知为 三角形，故，又，故，

34、由 可知，当B，P，A在同一条直线上时，取最小值，如图2，最小值为，此时的P点为该三角形的“费马点”，且有 ；已知当有一个内角大于或等于时，“费马点”为该三角形的某个顶点如图3，若，则该三角形的“费马点”为 点（2）如图4，在中，三个内角均小于，且，已知点P为的“费马点”，求的值； （3）如图5，设村庄A，B，C的连线构成一个三角形，且已知现欲建一中转站P沿直线向A，B，C三个村庄铺设电缆，已知由中转站P到村庄A，B，C的铺设成本分别为a元/，a元/，元/，选取合适的P的位置，可以使总的铺设成本最低为_元（结果用含a的式子表示）【答案】（1）等边；两点之间线段最短；A （2） （3）【解析】【

35、分析】（1）根据旋转的性质和两点之间线段最短进行推理分析即可得出结论；（2）根据（1）的方法将绕，点C顺时针旋转得到，即可得出可知当B，P，A在同一条直线上时，取最小值，最小值为，在根据可证明，由勾股定理求即可，（3）由总的铺设成本，通过将绕，点C顺时针旋转得到，得到等腰直角，得到，即可得出当B，P，A在同一条直线上时，取最小值，即取最小值为，然后根据已知和旋转性质求出即可【小问1详解】解：，为等边三角形；，又，故，由两点之间线段最短可知，当B，P，A在同一条直线上时，取最小值，最小值为，此时的P点为该三角形的“费马点”，又，；，三个顶点中，顶点A到另外两个顶点的距离和最小又已知当有一个内角大

36、于或等于时，“费马点”为该三角形的某个顶点该三角形的“费马点”为点A，故答案为：等边；两点之间线段最短；【小问2详解】将绕，点C顺时针旋转得到，连接，由（1）可知当B，P，A在同一条直线上时，取最小值，最小值为， ，又，由旋转性质可知：，最小值为，【小问3详解】总铺设成本当最小时，总的铺设成本最低，将绕，点C顺时针旋转得到，连接，由旋转性质可知：，当B，P，A在同一条直线上时，取最小值，即取最小值为， 过点作，垂足为，的最小值为总的铺设成本（元）故答案为：【点睛】本题考查了费马点求最值问题，涉及到的知识点有旋转的性质，等边三角形的判定与性质，勾股定理，以及两点之间线段最短等知识点，读懂题意，利

37、用旋转作出正确的辅助线是解本题的关键24. 如图1，平面直角坐标系中，抛物线过点，和，连接，点为抛物线上一动点，过点作轴交直线于点，交轴于点 （1）直接写出抛物线和直线的解析式；（2）如图2，连接，当为等腰三角形时，求的值；（3）当点在运动过程中，在轴上是否存在点，使得以，为顶点三角形与以，为顶点的三角形相似（其中点与点相对应），若存在，直接写出点和点的坐标；若不存在，请说明理由【答案】（1）抛物线：；直线： （2）或或 （3），或，或，【解析】【分析】（1）由题得抛物线的解析式为，将点代入求，进而得抛物线的解析式；设直线的解析式为，将点，的坐标代入求，进而得直线的解析式（2）由题得，分别求出

38、，对等腰中相等的边进行分类讨论，进而列方程求解；（3）对点在点左侧或右侧进行分类讨论，设法表示出各线段的长度，利用相似三角形的相似比求解，进而可得，的坐标【小问1详解】解：抛物线过点，抛物线的表达式为，将点代入上式，得，抛物线的表达式为，即设直线的表达式为，将点，代入上式，得，解得直线的表达式为【小问2详解】解：点在直线上，且，点的坐标为，当为等腰三角形时，若，则，即，解得若，则，即，解得或（舍去）若，则，即，解得（舍去）或综上，或或【小问3详解】解：点与点相对应，或若点在点左侧，则，当，即时，直线的表达式为，解得或（舍去），即，即，解得，当，即时，即，解得（舍去）或（舍去）若点点右侧，则，当，即时，直线的表达式为，解得或（舍去），即，解得，当，即时，即，解得或（舍去），综上，或，或，【点睛】本题是二次函数的综合应用，考查了待定系数法求函数解析式，等腰三角形的性质与判定，平面直角坐标系中两点距离的算法，相似三角形的性质与判定等，熟练掌握相关知识是解题的关键