2019年广西柳州市中考数学专题训练05：函数与几何图形的综合（含答案）

《2019年广西柳州市中考数学专题训练05：函数与几何图形的综合（含答案）》由会员分享，可在线阅读，更多相关《2019年广西柳州市中考数学专题训练05：函数与几何图形的综合（含答案）（15页珍藏版）》请在七七文库上搜索。

1、专题训练(五) 函数与几何图形的综合1.2017济宁 已知函数 y=mx2-(2m-5)x+m-2 的图象与 x 轴有两个公共点.(1)求 m 的取值范围 ,并写出当 m 取范围内最大整数时函数的解析式;(2)题(1)中求得的函数记为 C1. 当 nx-1 时,y 的取值范围是 1y-3n,求 n 的值; 函数 C2:y=m(x-h)2+k 的图象由函数 C1 的图象平移得到,其顶点 P 落在以原点为圆心,半径为 的圆内或圆上.设函数5C1 的图象顶点为 M,求点 P 与点 M 距离最大时函数 C2 的解析式.2.2017攀枝花改编 如图 ZT5-1,抛物线 y=x2+bx+c 与 x 轴交于

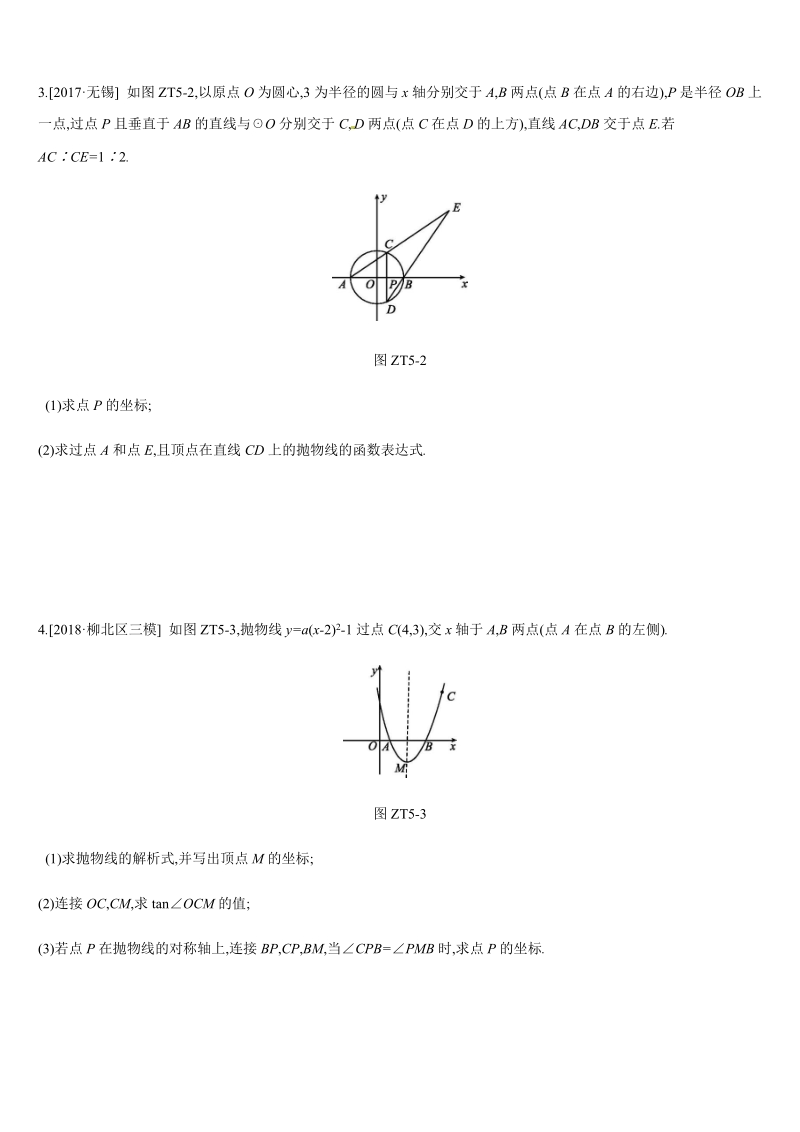
2、 A,B 两点,B 点坐标为(3,0),与 y 轴交于点 C(0,3).图 ZT5-1(1)求抛物线的解析式;(2)点 P 在 x 轴下方的抛物线上,过点 P 的直线 y=x+m 与直线 BC 交于点 E,与 y 轴交于点 F,求 PE+EF 的最大值.(3)点 D 为抛物线对称轴上一点.当BCD 是以 BC 为直角边的直角三角形时 ,求点 D 的坐标.3.2017无锡 如图 ZT5-2,以原点 O 为圆心,3 为半径的圆与 x 轴分别交于 A,B 两点(点 B 在点 A 的右边),P 是半径 OB 上一点,过点 P 且垂直于 AB 的直线与O 分别交于 C, D 两点(点 C 在点 D 的上

3、方), 直线 AC,DB 交于点 E.若AC CE=1 2.图 ZT5-2(1)求点 P 的坐标;(2)求过点 A 和点 E,且顶点在直线 CD 上的抛物线的函数表达式 .4.2018柳北区三模 如图 ZT5-3,抛物线 y=a(x-2)2-1 过点 C(4,3),交 x 轴于 A,B 两点(点 A 在点 B 的左侧).图 ZT5-3(1)求抛物线的解析式,并写出顶点 M 的坐标;(2)连接 OC,CM,求 tanOCM 的值;(3)若点 P 在抛物线的对称轴上,连接 BP,CP,BM,当CPB=PMB 时,求点 P 的坐标.5.2018柳北区 4 月模拟 如图 ZT5-4 ,在平面直角坐标系

4、 xOy 中,直线 l:y= x+m 与 x 轴,y 轴分别交于点 A 和点 B(0,-1),抛34物线 y= x2+bx+c 经过点 B,且与直线 l 的另一个交点为 C(4,n).12图 ZT5-4(1)求 n 的值和抛物线的解析式.(2)点 D 在抛物线上 ,且点 D 的横坐标 为 t(00.解得:m ,且 m0.2512当 m=2 时,函数解析式为 y=2x2+x.(2) 函数 y=2x2+x 图象开口向上 ,对称轴为直线 x=- ,14当 x- 时 ,y 随 x 的增大而减小.14当 nx-1时,y 的取值范围是 1y-3n,2n 2+n=-3n.n=-2 或 n=0(舍去).n=-

5、2. y= 2x2+x=2 x+ 2- ,14 18函数 C1 的图象顶点 M 的坐标为 - ,- .1418由图形可知当 P 为射线 MO 与圆的交点时,距离最大.点 P 在直线 OM 上,由 O(0,0),M - ,- 可求得直线的解析式为 y= x.1418 12设 P(a,b),则有 a=2b.根据勾股定理可得 PO2=(2b)2+b2=( )2,解得 b=1(负值已舍).5a=2.PM 最大时函数 C2 的解析式为 y=2(x-2)2+1.2.解:(1)由题意得 解得32+3+=0,=3, =-4,=3. 抛物线的解析式为 y=x2-4x+3.(2)方法 1(代数法 ):如图 ,过点

6、 P 作 PGCF 交 CB 于点 G,由题意知BCO=CFE=45,F(0,m),C(0,3),CFE 和GPE 均为等腰直角三角形,EF= CF= (3-m),PE= PG.22 22 22又易知直线 BC 的解析式为 y=-x+3.设 xP=t(1t3),则 PE= PG= (-t+3-t-m)= (-m-2t+3).22 22 22又t 2-4t+3=t+m,m=t 2-5t+3.PE+EF= (3-m)+ (-m-2t+3)= (-2t-2m+6)=- (t+m-3)=- (t2-4t)=- (t-2)2+4 ,22 22 22 2 2 2 2当 t=2 时,PE+EF 取最大值 4

7、 .2方法 2:(几何法)如图 ,由题易知直线 BC 的解析式为 y=-x+3,OC=OB=3,OCB=45.同理可知OFE=45,CEF 为等腰直角三角形.以 BC 为对称轴将FCE 对称得到FCE,作 PHCF于点 H则 PE+EF=PF= PH.2又 PH=yC-yP=3-yP.当 yP最小时 ,PE+EF 取最大值.抛物线的顶点坐标为(2,-1),当 yP=-1 时,(PE+EF) max= (3+1)=4 .2 2(3)由(1)知对称轴为直线 x=2,设 D(2,n),如图 .当BCD 是以 BC 为直角边的直角三角形 ,且 D 在 BC 上方 D1 位置时,由勾股定理得 C +BC

8、2=B ,21 21即(2-0) 2+(n-3)2+(3 )2=(3-2)2+(0-n)2,解得 n=5;2当BCD 是以 BC 为直角边的直角三角形 ,且 D 在 BC 下方 D2 位置时,由勾股定理得 B +BC2=C ,22 22即(2-3) 2+(n-0)2+(3 )2=(2-0)2+(n-3)2,解得 n=-1.2当BCD 是以 BC 为直角边的直角三角形时 ,D 点坐标为(2,5)或(2, -1).3.解:(1)过点 E 作 EFx 轴于点 F,CDAB ,CDEF ,PC=PD.ACPAEF,BPDBFE.AC CE=1 2,AC AE=1 3. = = , = = .AF= 3

9、AP,BF=3PB.AF-BF=AB.13B133AP- 3PB=AB.又O 的半径为 3,设 P(m,0),3(3+m) -3(3-m)=6,m=1.P(1,0).(2)P(1,0),OP=1,A( -3,0).OA=3,AP=4,BP= 2.AF=12.连接 BC.AB 是直径,ACB=90 .CDAB ,ACPCBP, = .CP 2=APBP=42=8.CP=2 (负值已舍).EF=3CP=6 .2 2E(9, 6 ).2抛物线的顶点在直线 CD 上,CD 是抛物线的对称轴,抛物线过点(5,0).设抛物线的函数表达式为 y=ax2+bx+c.根据题意得 0=9-3+,0=25+5+,6

10、2=81+9+,解得=28,=- 24,=-1528,抛物线的函数表达式为 y= x2- x- .28 24 15284.解:(1)由抛物线 y=a(x-2)2-1 过点 C(4,3),得 3=a(4-2)2-1,解得 a=1,抛物线的解析式为 y=(x-2)2-1,顶点 M 的坐标为(2,-1) .(2)如图,连接 OM,OC 2=32+42=25,OM2=22+12=5,CM2=22+42=20,CM 2+OM2=OC2,OMC=90.OM= ,CM=2 ,tanOCM= = = .5 552512(3)如图,过 C 作 CN 垂直于对称轴 ,垂足 N 在对称轴上,取一点 E,使 EN=C

11、N=2,连接 CE,EM=6.当 y=0 时,(x-2) 2-1=0,解得 x1=1,x2=3,A(1,0), B(3,0).CN=EN, CEP=PMB=CPB=45,EPB=EPC+CPB= PMB+PBM,EPC=PBM,CEP PMB, = ,易知 MB= ,CE=2 , 2 2 = ,解得 PM=3 ,6-2 22 5P 点坐标为(2,2+ )或(2,2- ).5 55.解:(1)直线 l:y= x+m 经过点 B(0,-1),34m=-1,直线 l 的解析式为 y= x-1.34直线 l:y= x-1 经过点 C(4,n),34n= 4-1=2.34抛物线 y= x2+bx+c 经

12、过点 C(4,2)和点 B(0,-1),12 1242+4+=2,=-1, 解得 =-54,=-1,抛物线的解析式为 y= x2- x-1.12 54(2)令 y=0,则 x-1=0,34解得 x= ,43点 A 的坐标为 ,0 ,43OA= .43在 Rt OAB 中,OB=1,AB= = = .2+2 (43) 2+1253DEy 轴,ABO= DEF,在矩形 DFEG 中,EF=DEcosDEF=DE = DE,35DF=DEsinDEF=DE = DE,45p=2( DF+EF)=2 + DE= DE,4535 145点 D 的横坐标为 t(0t4),D t, t2- t-1 ,E t

13、, t-1 ,12 54 34DE= t-1 - t2- t-1 =- t2+2t,34 12 54 12p= - t2+2t =- t2+ t,145 12 75 285p=- (t-2)2+ ,且- 0,75 285 75当 t=2 时,p 有最大值 .285(3)AOB 绕点 M 沿逆时针方向旋转 90,A 1O1y 轴,B 1O1x 轴.设点 A1 的横坐标为 x,如图 ,点 O1,B1 在抛物线上时 ,点 O1 的横坐标为 x,点 B1 的横坐标为 x+1, x2- x-1= (x+1)2- (x+1)-1,12 54 12 54解得 x= .34如图 ,点 A1,B1 在抛物线上时

14、,点 B1 的横坐标为 x+1,点 A1 的纵坐标比点 B1 的纵坐标大 ,43 x2- x-1= (x+1)2- (x+1)-1+ ,12 54 12 54 43解得 x=- .712综上所述,点 A1 的横坐标为 或 - .34 7126.解:(1)令 y=0,得 x2- x- =0,33 233 3解得 x1=-1,x2=3,点 A(-1,0),B(3,0).点 E(4,n)在抛物线上 ,n= 42- 4- = ,33 233 3533即点 E ,(4,533)设直线 AE 的解析式为 y=kx+b,则 ,解得-+=0,4+=533 =33,=33,直线 AE 的解析式为 y= x+ .

15、33 33(2)令 y= x2- x- 中 x=0,得 y=- ,33 233 3 3C(0,- ).由(1)得点 E ,3 (4,533)直线 CE 的解析式为 y= x- .233 3过点 P 作 PH y 轴,交 CE 于点 H,如图 ,设点 P t, t2- t- ,则 H t, t- ,33 233 3 233 3PH= t- - =- t2+ t,233 3(332-233- 3) 33 433S PCE =SPHC +SPHE = PH12 |-|= 412(- 332+433)=- t2+ t233 833=- (t2-4t)233=- (t-2)2+ .233 833- 0,

16、233当 t=2 时,S PCE 最大,此时点 P(2,- ).3C(0,- ),3PCx 轴.B(3,0), K 为 BC 的中点,K ,- .32 32如图 ,作点 K 关于 CP,CD 的对称点 K1,K2,连接 K1K2,分别交 CP,CD 于点 M,N.此时 KM+MN+NK 最小,易知 K1 ,- .32332OC= ,OB=3,OD=1,3OCB=60,OCD= 30,CD 平分OCB,点 K2 在 y 轴上 .CK=OC= ,3点 K2 与原点 O 重合,KM+MN+NK=K 1M+MN+NO=OK1= =3,(32)2+(-332)2KM+MN+NK 的最小值为 3.(3)存 在.如图 ,点 Q 的坐标分别为 Q1(3,2 ),Q2 3, ,Q3 3,- ,3-43+2213 235Q4 3, .-43-2213