2019年中考数学临考冲刺专题练测：几何探究题（含解析）

《2019年中考数学临考冲刺专题练测：几何探究题（含解析）》由会员分享，可在线阅读，更多相关《2019年中考数学临考冲刺专题练测：几何探究题（含解析）（20页珍藏版）》请在七七文库上搜索。

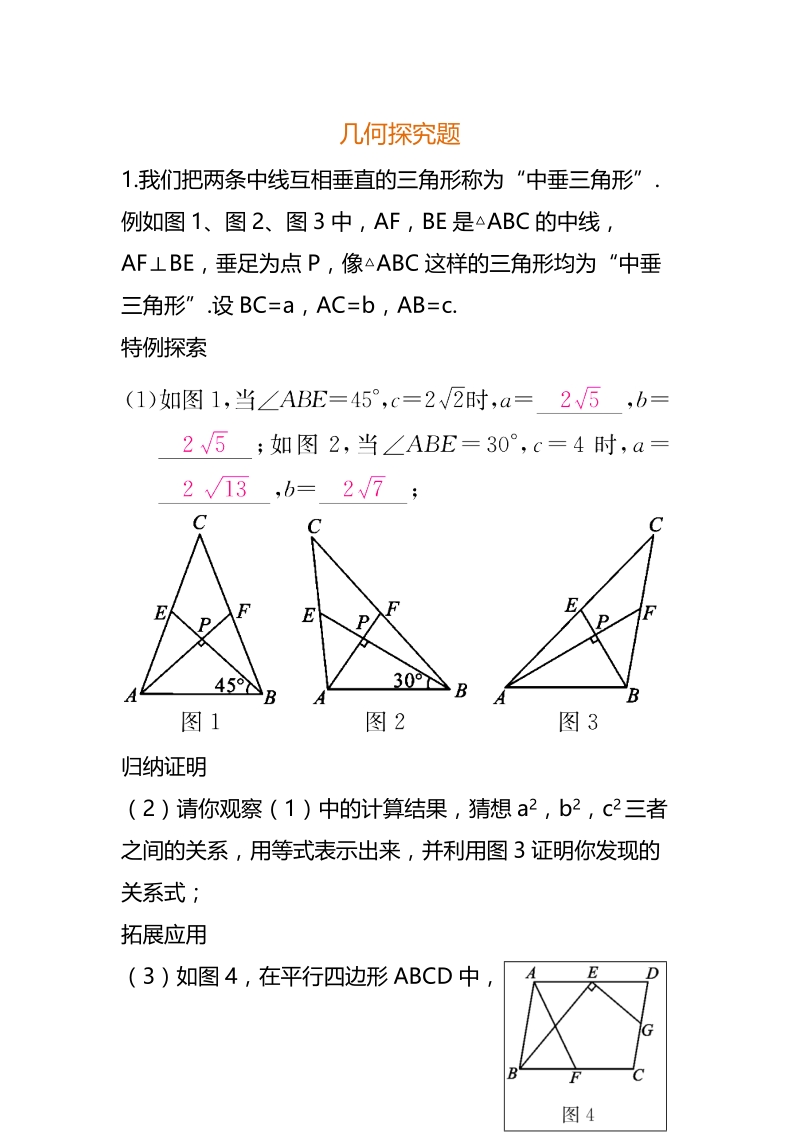
1、几何探究题1.我们把两条中线互相垂直的三角形称为“中垂三角形”.例如图 1、图 2、图 3 中，AF，BE 是 ABC的中线，AFBE，垂足为点 P，像ABC 这样的三角形均为“中垂三角形”.设 BC=a，AC=b ，AB=c.特例探索归纳证明（2）请你观察（ 1）中的计算结果，猜想 a2，b 2，c 2三者之间的关系，用等式表示出来，并利用图 3 证明你发现的关系式；拓展应用（3）如图 4，在平行四边形 ABCD 中，点 E，F，G 分别是 AD，BC，CD 的中点，BEEG，AD=2 ，AB=3.求 AF 的长 .解：（2）猜想 a2，b 2，c 2三者之间的关系是 a2+b2=5c2.证

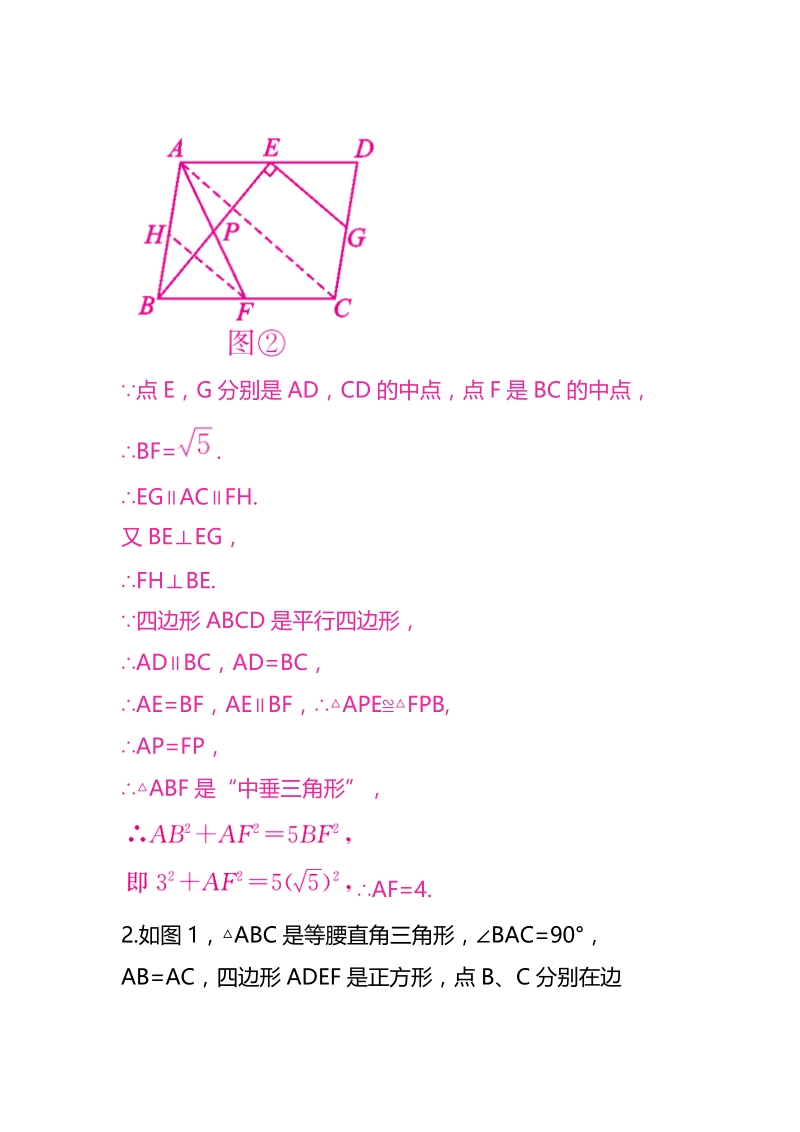
2、明如下：如图，连接 EF.AF，BE 是ABC 的中线，EF是ABC 的中位线，设 PF=m，PE=n ，则 AP=2m，PB=2n.在 RtAPB中，（2m） 2+（2n） 2=c2;在 RtAPE中，（2m ） 2+n2=（b2） 2;在 RtBPF中，m 2+（2n ） 2=（a2） 2.a2+b2=5c2.（3）如图 ，取 AB 的中点 H，连接 FH，AC，设AF，BE 交于点 P.点 E，G 分别是 AD，CD 的中点，点 F 是 BC 的中点，BF= .EGACFH.又 BEEG，FHBE.四边形 ABCD 是平行四边形，ADBC，AD=BC，AE=BF，AEBF，APEFPB,

3、AP=FP，ABF是 “中垂三角形”，AF=4.2.如图 1， ABC是等腰直角三角形，BAC=90，AB=AC，四边形 ADEF 是正方形，点 B、C 分别在边AD、AF 上，此时 BD=CF，BDCF 成立.（1）当ABC 绕点 A 逆时针旋转 （090）时，如图 2，BD=CF 成立吗？若成立，请证明；若不成立，请说明理由.（2）当ABC 绕点 A 逆时针旋转 45时，如图 3，延长 DB交 CF 于点 H.求证：BDCF；（1）解： BD=CF 成立.证明：AC=AB,CAF=BAD=,AF=AD,ABDACF,BD=CF.（2）证明：由（1 ）得，ABDACF，HFN=ADN.又HN

4、F=AND，NHF=NAD=90，HDHF，即 BDCF.解：如图，连接 DF，延长 AB，与DF 交于点 M.在MAD 中，MAD=MDA=45，BMD=90.MDB=HDF，BMDFHD.3.问题引入：（1）如图 ，在ABC 中，点 O 是ABC 和ACB 平分线的交点，若A=，则 BOC= 90+1/2 （用含 的式子表示）；如图，CBO=1/3ABC，BCO=1/3ACB，若A=，则BOC= 120+1/3 （用含 的式子表示）.拓展研究：（2）如图 ，CBO=1/3DBC，BCO=1/3ECB，若A=，请猜想BOC= 120-1/3 （用含 的式子表示），并说明理由.类比研究：（3）

5、BO,CO 分别是ABC 的外角DBC,ECB 的 n 等分线，它们交于点O，CBO=1/nDBC，BCO=1/nECB，A=，请猜想BOC=4.如图，已知正方形 ABCD 的边长为 4，E 是射线 CB 上的一个动点，过点 D 作 DFDE，交 BA 的延长线于点 F，EF交对角线 AC 所在的直线于点 M，DE 交 AC 于点 N.（1）求证： CE=AF；（2）设 CE=x，AMF 的面积为 y，求 y 与 x 之间的函数关系式，并写出自变量 x 的取值范围；（3）随着点 E 在射线 CB 上运动，NAMC 的值是否会发生变化？若不变，请求出 NAMC 的值；若变化，请说明理由.（1）证

6、明：在正方形 ABCD 中，ADC=90.FDE=ADC=90，FDA=CDE.又 DC=AD，DCE=DAF=90，CDEADF，CE=AF.（2）解：当点 E 在 BC 上时，如图, 过 M 作 MGAB 于 G.CBAB，MGBC.设 MG=h.又GAM=45，AG=MG=h.图当点 E 在 CB 的延长线上时，如图,过M 作 MGBF 于 G，则 MGCE，（3）解： NAMC 的值不变.如图, 过 E 作 EGAB交 AC于 G，连接 DM，则EGC=GCE=45 ，EG=EC=AF，图FAM=MGE=135.又AMF=GME，FAMEGM，ME=FM.由（1）可得 FDE是等腰直角

7、三角形，DMEF，MDE=45，则DNA=MDC=45+CDN，DAN=DCM=45，ANDCDM，5.如图，矩形 ABCD 的对角线 AC，BD 相交于点 O，COD 关于 CD 对称的图形为CED.（1）求证：四边形 OCED 是菱形；（2）连接 AE，若 AB=6 cm，BC= cm.求 sinEAD的值；若点 P 为线段 AE 上一动点（不与点 A 重合），连接OP，一动点 Q 从点 O 出发，以 1 cm/s 的速度沿线段 OP匀速运动到点 P，再以 1.5 cm/s 的速度沿线段 PA 匀速运动到点 A，到达点 A 后停止运动，当点 Q 沿上述路线运动到点 A 所需要的时间最短时，

8、求 AP 的长和点 Q 走完全程所需的时间.（1）证明： 四边形 ABCD 是矩形,OD=OB=OC=OA.CED和 COD关于 CD 对称，DE=DO，CE=CO ，DE=EC=CO=OD，四边形 OCED 是菱形.（2）解： 如图，设 AE 交 CD于 K.四边形 OCED 是菱形，DEAC，DE=OC=OA，作 PFAD 于 F.易知 PF=APsinDAE=2/3AP.当点 Q 沿上述路线运动到点 A 所需要的时间最短时，AP的长为 32cm，点 Q 走完全程所需的时间为 3s.6.如图 1，点 O 是正方形 ABCD 两对角线的交点，分别延长 OD 到点 G，OC 到点 E，使 OG

9、=2OD，OE=2OC，然后以 OG、OE 为邻边作正方形 OEFG，连接 AG，DE.（1）求证： DEAG；（2）正方形 ABCD 固定，将正方形 OEFG 绕点 O 逆时针旋转 角（0 360）得到正方形 OEFG，如图 2.在旋转过程中，当OAG 是直角时，求 的度数；若正方形 ABCD 的边长为 1，在旋转过程中，求 AF长的最大值和此时 的度数，直接写出结果，不必说明理由.（1）证明：如图 1，延长 ED 交 AG 于点 H.点 O 是正方形 ABCD 两对角线的交点，OA=OD=OC，OAO D.OG=2OD，OE=2OC ，OG=OE.在AOG 和DOE 中，OA=OD,AOG

10、=DOE,OG=OE,AOGDOE，AGO=DEO.AGO+GAO=90，GAO+DEO=90，AHE=90，即 DEAG.（2）解： 在旋转过程中，OAG 成为直角有两种情况：（） 由 0增大到 90过程中，当OAG=90时，OA=OD=12OG=12OG，AGO=30.OAOD，OAAG，ODAG ，DOG=AGO=30，即 =30.（） 由 90增大到 180过程中，当OAG=90时，同理可求BOG=30，=180-30=150.综上所述，当OAG 是直角时， 的度数是 30或 150.AF长的最大值是 此时 的度数是 315.如图，当旋转到 A、O、F在一条直线上时，AF的长最大.正方

11、形 ABCD 的边长为 1，7.如图 1，将三角形纸片 ABC 沿中位线 EH 折叠，使点 A的对称点 D 落在 BC 边上，再将纸片分别沿等腰三角形BED 和等腰三角形 DHC 的底边上的高线 EF，HG 折叠，折叠后的 3 个三角形拼合形成一个矩形.类似地，对多边形进行折叠，若翻折后的图形恰能拼合成一个无缝隙、无重叠的矩形，这样的矩形称为叠合矩形.（1）将平行四边形纸片 ABCD 按图 2 的方式折叠成一个叠合矩形 AEFG，则操作形成的折痕分别是线段 AE ， GE ;S 矩形 AEFGS平行四边形 ABCD= 12 .（2）平行四边形纸片 ABCD 还可以按图 3 的方式折叠成一个叠合

12、矩形 EFGH，若 EF=5，EH=12，求 AD 的长;（3）如图 4，四边形纸片 ABCD 满足ADBC，ADBC，ABBC，AB=8，CD=10.小明把该纸片折叠，得到叠合正方形.请你帮助小明画出叠合正方形的示意图，并直接写出 AD，BC 的长.解：（1） AEGF12（2）四边形 EFGH 是叠合矩形，FEH=90.又 EF=5，EH=12，设点 D 的对称点为 N，点 B 的对称点为 M.由折叠可知，DH=HN，AH=HM ，CF=FN.易证AEHCGF，CF=AH，AD=DH+AH=HN+FN=FH=13.8.我们定义：如图 1，在ABC 中，把 AB 绕点 A 顺时针旋转 （0

13、180）得到 AB，把 AC 绕点 A 逆时针旋转得到 AC，连接 BC.当 +=180时，我们称ABC是ABC 的“旋补三角形”，ABC边 BC上的中线 AD 叫做ABC的“ 旋补中线 ”，点 A 叫做“旋补中心”.特例感知：（1）在图 2，图 3 中，ABC是ABC 的“旋补三角形”，AD 是ABC 的“旋补中线”.如图 2，当 ABC为等边三角形时，AD 与 BC 的数量关系为 AD= 1/2 BC；如图 3，当 BAC=90，BC=8 时，AD 长为 4 .猜想论证：（2）在图 1 中，当 ABC为任意三角形时，猜想 AD 与BC 的数量关系，并给予证明.拓展应用:（3）如图 4，在四

14、边形 ABCD，C=90，D=150，BC=12，CD=2 ，DA=6.在四边形内部是否存在点 P，使PDC 是PAB 的“旋补三角形”？若存在，给予证明，并求PAB 的“旋补中线”长；若不存在，说明理由.解：（1） 1/24（2）结论： AD=1/2BC.证明：如图，延长 AD 到 M，使得 AD=DM，连接 BM，CM.BD=DC，AD=DM.四边形 ACMB是平行四边形，AC=BM=AC.BAC+BAC=180，BAC+ABM=180，BAC=MBA.又 AB=AB，AC=BM,BACABM，BC=AM，AD=1/2BC.（3）存在 .证明：如图，延长 AD 交 BC 的延长线于 M，作

15、 BEAD 于 E，作线段 BC 的垂直平分线交 BE 于P，交 BC 于 F，连接PA、PD 、PC ，作PCD 的中线PN,连接 DF.ADC=150，MDC=30.在 RtDCM中，CM=2，DM=4，M=60.在 RtBEM中，BEM=90，BM=14，MBE=30，EM=1/2BM=7，DE=EM-DM=3.AD=6,BEAD，PFBC,AE=DE.PA=PD，PB=PC.CDF=60=CPF.易证FCPCFD，CD=PF.CDPF，四边形 CDPF 是矩形，CDP=90，ADP=ADC-CDP=60.ADP是等边三角形，ADP=60.BPF=CPF=60，BPC=120，APD+BPC=180，PDC是PAB 的 “旋补三角形”.在 RtPDN中，