2017年贵州省贵阳市高考数学二模试卷（理科）含答案解析

《2017年贵州省贵阳市高考数学二模试卷（理科）含答案解析》由会员分享，可在线阅读，更多相关《2017年贵州省贵阳市高考数学二模试卷（理科）含答案解析（21页珍藏版）》请在七七文库上搜索。

1、2017 年贵州省贵阳市高考数学二模试卷（理科）一、选择题：本大题共 12 小题，每小题 5 分，在每小题给出的四个选项中，只有一项是符合题目要求的.1 （5 分）设 i 为虚数单位，若复数 在复平面内对应的点为（1，2） ，则 z（  ）A2+i B2i C1+2i D12i2 （5 分）A、B 为两个非空集合，定义集合 ABx| xA 且 xB，若A 2，1， 0，1，2，Bx|（x 1） （x+2）0，则 AB（  ）A2 B1 ，2 C 2，1，2 D 2，1，03 （5 分）已知向量 ， ，| |2，| |1，若 （ ）2，则向量 与 的夹角为（  ）A

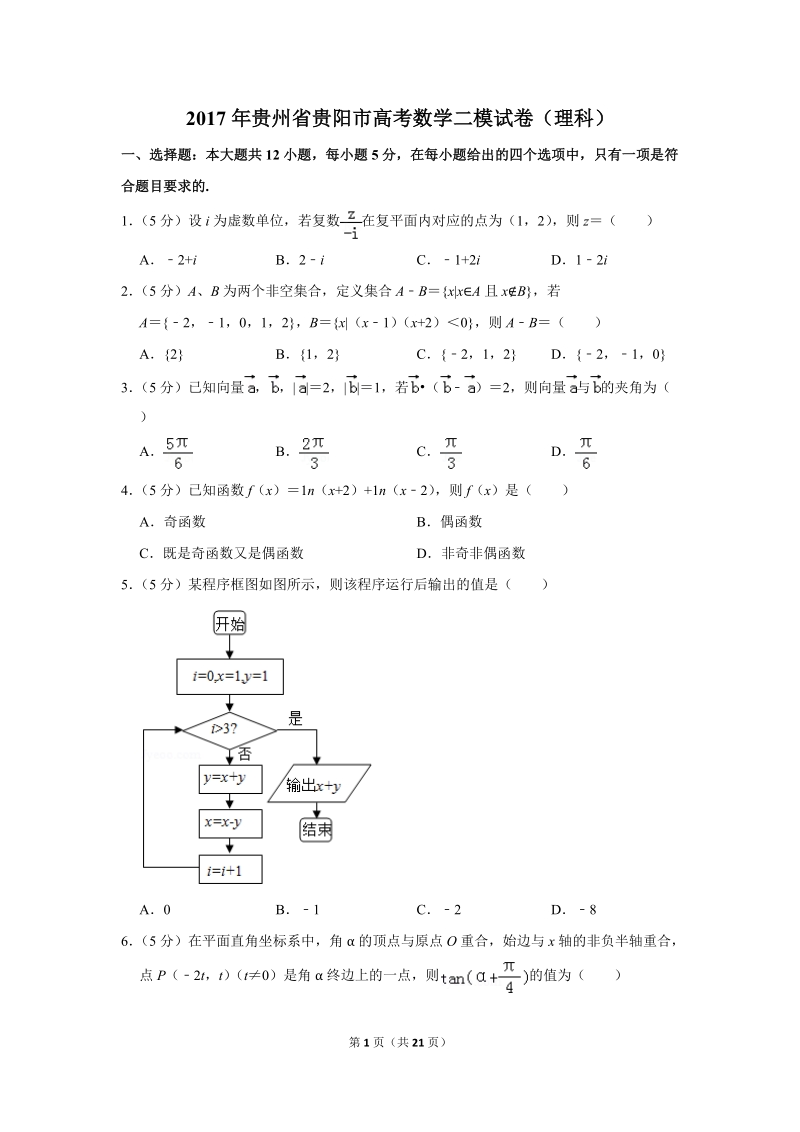
2、 B C D4 （5 分）已知函数 f（x ）1n（x+2）+1n（x2） ，则 f（x）是（  ）A奇函数 B偶函数C既是奇函数又是偶函数 D非奇非偶函数5 （5 分）某程序框图如图所示，则该程序运行后输出的值是（  ）A0 B1 C2 D86 （5 分）在平面直角坐标系中，角 的顶点与原点 O 重合，始边与 x 轴的非负半轴重合，点 P（ 2t，t） （t0）是角 终边上的一点，则 的值为（  ）第 2 页（共 21 页）A B3 C D7 （5 分）若 的展示式中 x3 的系数为 30，则实数 a（  ）A6 B6 C5 D58 （5 分）已知实数

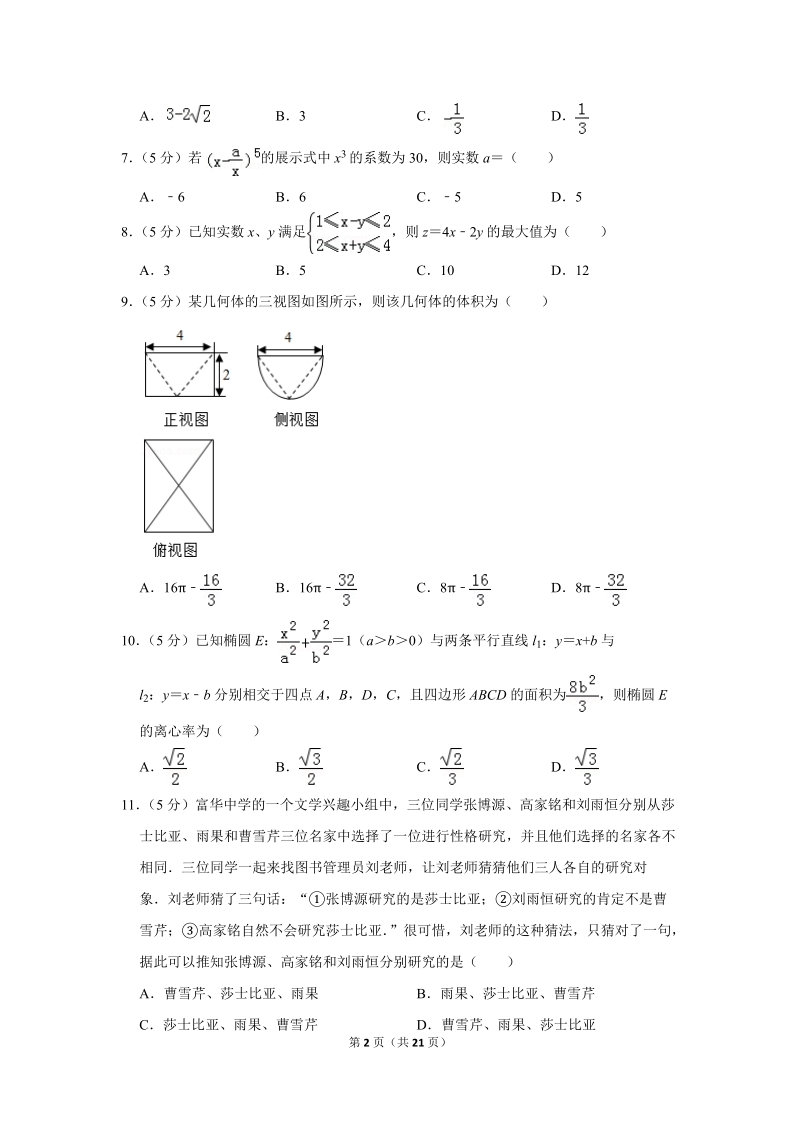
3、 x、y 满足 ，则 z4x 2y 的最大值为（  ）A3 B5 C10 D129 （5 分）某几何体的三视图如图所示，则该几何体的体积为（  ）A16 B16 C8 D810 （5 分）已知椭圆 E： 1（ab0）与两条平行直线 l1：yx+b 与l2：yx b 分别相交于四点 A，B，D ，C，且四边形 ABCD 的面积为 ，则椭圆 E的离心率为（  ）A B C D11 （5 分）富华中学的一个文学兴趣小组中，三位同学张博源、高家铭和刘雨恒分别从莎士比亚、雨果和曹雪芹三位名家中选择了一位进行性格研究，并且他们选择的名家各不相同三位同学一起来找图书管理员刘老师

4、，让刘老师猜猜他们三人各自的研究对象刘老师猜了三句话：“张博源研究的是莎士比亚；刘雨恒研究的肯定不是曹雪芹； 高家铭自然不会研究莎士比亚 ”很可惜，刘老师的这种猜法，只猜对了一句，据此可以推知张博源、高家铭和刘雨恒分别研究的是（  ）A曹雪芹、莎士比亚、雨果 B雨果、莎士比亚、曹雪芹C莎士比亚、雨果、曹雪芹 D曹雪芹、雨果、莎士比亚第 3 页（共 21 页）12 （5 分）已知函数 f（x ）x 2，g（x）1nx，g'（x）为 g（x）的导函数若存在直线 l 同为函数 f（x ）与 g'（ x）的切线，则直线 l 的斜率为（   ）A B2 C4 D二、填

5、空题：本大题共 4 小题，每小题 5 分13 （5 分）定积分 的值为     14 （5 分）在ABC 中，A，B，C 的对边分别是 a，b，c，若c2acosB+bcosA，ab3，则ABC 的周长为      15 （5 分）从集合2，3，4 ，5 中随机抽取一个数 a，从集合 4，6，8中随机抽取一个数b，则向量 （a，b）与向量 （2，1）垂直的概率为     16 （5 分）已知等腰直角ABC 的斜边 BC2，沿斜边的高线 AD 将ABC 折起，使二面角 BADC 为 ，则四面体 ABCD 的外接球的表面积为 &

6、nbsp;   三、解答题：解答应写出文字说明、证明过程或演算步骤17 （12 分）设 Sn 是数列a n的前 n 项和，a n0，且 4Sna n（a n+2） （）求数列a n的通项公式；（）设 bn ，T nb 1+b2+bn，求证： Tn 18 （12 分）医学上某种还没有完全攻克的疾病，治疗时需要通过药物控制其中的两项指标 H 和 V现有三种不同配方的药剂，根据分析， A，B，C 三种药剂能控制 H 指标的概率分别为 0.5，0.6，0.75，能控制 V 指标的概率分别是 0.6，0.5，0.4，能否控制 H 指标与能否控制 V 指标之间相互没有影响（）求 A，B，C 三种

7、药剂中恰有一种能控制 H 指标的概率；（）某种药剂能使两项指标 H 和 V 都得到控制就说该药剂有治疗效果求三种药剂中有治疗效果的药剂种数 X 的分布列19 （12 分）如图，棱柱 ABCDA 1B1C1D1 中，底面 ABCD 是平行四边形，侧棱 AA1底面 ABCD，AB 1，AC ，BC BB 12（）求证：AC平面 ABB1A1；（）求二面角 AC 1DC 的平面角的余弦值第 4 页（共 21 页）20 （12 分）已知椭圆 C： 1（a0）的焦点在 x 轴上，且椭圆 C 的焦距为2（）求椭圆 C 的标准方程；（）过点 R（4，0）的直线 l 与椭圆 C 交于两点 P，Q，过 P 作

8、PNx 轴且与椭圆 C交于另一点 N，F 为椭圆 C 的右焦点，求证：三点 N，F，Q 在同一条直线上21 （12 分）已知函数 f（x ）（x 22x）1nx+ax 2+2，g（x）f（x）x2（）当 a1 时，求 f（x）在（1，f（1） ）处的切线方程；（）若 a0 且函数 g（x）有且仅有一个零点，求实数 a 的值；（）在（）的条件下，若 e2 xe 时，g（x）m 恒成立，求实数 m 的取值范围请考生在第 22、23 题中任选一题作答如果多做，则按所做的第一题记分.作答时用 2B 铅笔在答题卡上把所选题目对应题号后的方框涂黑选修 4-4：坐标系与参数方程选讲22 （10 分）在平面直

9、角坐标系 xoy 中，曲线 C 的参数方程为 （t 为参数） ，以 O为极点 x 轴的正半轴为极轴建极坐标系，直线 l 的极坐标方程为 （cos sin ）4，且与曲线 C 相交于 A，B 两点（）在直角坐标系下求曲线 C 与直线 l 的普通方程；（）求AOB 的面积选修 4-5：不等式选讲23已知函数 f（x ）m|x1|， （m0） ，且 f（x+1） 0 的解集为3，3（）求 m 的值；（）若正实数 a，b，c 满足 ，求证：a+2b+3c3第 5 页（共 21 页）2017 年贵州省贵阳市高考数学二模试卷（理科）参考答案与试题解析一、选择题：本大题共 12 小题，每小题 5 分，在每小

10、题给出的四个选项中，只有一项是符合题目要求的.1 （5 分）设 i 为虚数单位，若复数 在复平面内对应的点为（1，2） ，则 z（  ）A2+i B2i C1+2i D12i【分析】由复数 在复平面内对应的点为（1，2） ，得到 1+2i，化简即可【解答】解：复数 在复平面内对应的点为（1，2） ，则 1+2i，z2i，故选：B【点评】本题考查复数代数形式的混合运算，复数与复平面内对应点之间的关系属于基础题2 （5 分）A、B 为两个非空集合，定义集合 ABx| xA 且 xB，若A 2，1， 0，1，2，Bx|（x 1） （x+2）0，则 AB（  ）A2 B1 ，2 C

11、 2，1，2 D 2，1，0【分析】先分别求出集合 A、B，由此能求出 AB【解答】解：A、B 为两个非空集合，定义集合 ABx |xA 且 xB，A 2，1， 0，1，2，B x|（x1） （x +2）0x|2x1，AB2，1，2故选：C【点评】本题考查集合 AB 的求法，是基础题，解题时要认真审题，注意集合 AB的定义的合理运用3 （5 分）已知向量 ， ，| |2，| |1，若 （ ）2，则向量 与 的夹角为（  ）A B C D第 6 页（共 21 页）【分析】根据条件容易求出 ，进而可求出 的值，从而得出向量与 的夹角【解答】解： ； ； ；向量 的夹角为 故选：B【点评】

12、考查向量数量积的运算，向量夹角的余弦公式，以及向量夹角的范围4 （5 分）已知函数 f（x ）1n（x+2）+1n（x2） ，则 f（x）是（  ）A奇函数 B偶函数C既是奇函数又是偶函数 D非奇非偶函数【分析】根据题意，对于函数 f（x ） ，先分析其定义域可得函数 f（x）的定义域为x|x2，不关于原点对称，由函数奇偶性的性质可得答案【解答】解：函数 f（x ）1n（x+2）+1n（x2） ，则有 ，解可得 x2，即函数 f（x）的定义域为 x|x2，不关于原点对称，则 f（x）是非奇非偶函数；故选：D【点评】本题考查函数奇偶性的判定，注意要先分析函数的定义域5 （5 分）某程序

13、框图如图所示，则该程序运行后输出的值是（  ）第 7 页（共 21 页）A0 B1 C2 D8【分析】分析程序中各变量、各语句的作用，再根据流程图所示的顺序，循环可得结论【解答】解：模拟程序的运行，可得：i0，x1，y1，不满足条件 i3，y 2，x1，i1，不满足条件 i3，y 1，x2，i2，不满足条件 i3，y 1，x1，i3，不满足条件 i3，y 2，x1，i4，满足条件 i3，退出循环，输出 x+y 的值为1故选：B【点评】本题给出程序框图，要我们求出最后输出值，着重考查了算法语句的理解和循环结构等知识，属于基础题6 （5 分）在平面直角坐标系中，角 的顶点与原点 O 重合

14、，始边与 x 轴的非负半轴重合，点 P（ 2t，t） （t0）是角 终边上的一点，则 的值为（  ）A B3 C D【分析】利用三角函数的定义，和角的正切公式，即可得出结论【解答】解：点 P（2t，t） （t 0）是角 终边上的一点，tan ，第 8 页（共 21 页） 故选：D【点评】本题考查三角函数的定义，和角的正切公式，考查学生的计算能力，比较基础7 （5 分）若 的展示式中 x3 的系数为 30，则实数 a（  ）A6 B6 C5 D5【分析】利用通项公式即可得出【解答】解： 的展示式中通项公式：T r+1 x5r （a）r x5 2r令 52r3，解得 r1x 3

15、 的系数为 30，则实数 a6故选：A【点评】本题考查了二项式定理的应用，考查了推理能力与计算能力，属于基础题8 （5 分）已知实数 x、y 满足 ，则 z4x 2y 的最大值为（  ）A3 B5 C10 D12【分析】作出不等式组对应的平面区域，利用目标函数的几何意义，利用平移法进行求解即可【解答】解：作出实数 x、y 满足 的可行域，如图： 解得A（3，1） ，作出直线 l：4x 2y0，平移直线 l，当它过点 A（3，1）时，z4x2y 取得最大值10故选：C第 9 页（共 21 页）【点评】本题主要考查线性规划的应用，根据条件结合目标函数的几何意义，利用平移法是解决本题的关键

16、9 （5 分）某几何体的三视图如图所示，则该几何体的体积为（  ）A16 B16 C8 D8【分析】由三视图可知：该几何体为一个半圆柱挖取一个倒立的四棱锥【解答】解：由三视图可知：该几何体为一个半圆柱挖取一个倒立的四棱锥该几何体的体积 V 8 故选：D【点评】本题考查了三棱台的三视图的有关知识、圆柱与四棱锥的体积计算公式，考查了推理能力与计算能力，属于中档题10 （5 分）已知椭圆 E： 1（ab0）与两条平行直线 l1：yx+b 与第 10 页（共 21 页）l2：yxb 分别相交于四点 A，B，D ，C，且四边形 ABCD 的面积为 ，则椭圆 E的离心率为（  ）A B

17、 C D【分析】联立直线与椭圆方程，求得 A 坐标，即求得边 AB，利用点到直线的距离公式求得边 AB 上的高，即可表示面积，列式求解【解答】解：如图所示，联立 （a 2+b2）x 2+2ba2x0，可得点 A 的横坐标为 AB 又因为原点到 AB 的距离 d四边形 ABCD 的面积为 AB2d 整理得：a 22b 2，椭圆 E 的离心率为 e 故选：A【点评】本题考查了椭圆的离心率，涉及到了点到直线的距离公式，属于中档题11 （5 分）富华中学的一个文学兴趣小组中，三位同学张博源、高家铭和刘雨恒分别从莎士比亚、雨果和曹雪芹三位名家中选择了一位进行性格研究，并且他们选择的名家各不相同三位同学一

18、起来找图书管理员刘老师，让刘老师猜猜他们三人各自的研究对象刘老师猜了三句话：“张博源研究的是莎士比亚；刘雨恒研究的肯定不是曹第 11 页（共 21 页）雪芹； 高家铭自然不会研究莎士比亚 ”很可惜，刘老师的这种猜法，只猜对了一句，据此可以推知张博源、高家铭和刘雨恒分别研究的是（  ）A曹雪芹、莎士比亚、雨果 B雨果、莎士比亚、曹雪芹C莎士比亚、雨果、曹雪芹 D曹雪芹、雨果、莎士比亚【分析】分别假设， ， 正确，推导各人研究对象，得出结论【解答】解：（1）若为真，则 为真，不符合题意，故 为假，即张博源研究的是曹雪芹或雨果；（2）若 为真，则 为假，则张博源研究的是曹雪芹，高家铭研究莎

19、士比亚，刘雨研究雨果，符合题意；（3）若 为真，则 为假，故而刘雨研究曹雪芹，张博源研究雨果，高家铭研究莎士比亚，此时得出为假，矛盾综上，张博源研究的是曹雪芹，高家铭研究莎士比亚，刘雨研究雨果故选：A【点评】本题考查了合情推理，属于中档题12 （5 分）已知函数 f（x ）x 2，g（x）1nx，g'（x）为 g（x）的导函数若存在直线 l 同为函数 f（x ）与 g'（ x）的切线，则直线 l 的斜率为（   ）A B2 C4 D【分析】分别设出直线 l 与两个函数所对应曲线的切点，求出切线方程，由两切线系数相等列式求出切点横坐标，则答案可求【解答】解：由 g（x）

20、1nx，得 g'（x ） ，设直线 l 与 f（x）的切点为（ ） ，则 f（x 1） 2x1，直线 l 的方程为 y ，即 ；再设 l 与 g'（x ）的切点为（ ） ，则 ，直线 l 的方程为 ，即 第 12 页（共 21 页） ，解得 x12直线 l 的斜率为 2x14故选：C【点评】本题考查利用导数研究过去线上某点处的切线方程，函数在曲线上某点处的导数，就是函数在该点处的导数值，是中档题二、填空题：本大题共 4 小题，每小题 5 分13 （5 分）定积分 的值为 e1 【分析】根据微积分基本定理计算【解答】解：（ +ex x）x 2+ex ， （ +ex x） （ ）1

21、e1故答案为：e1【点评】本题考查了微积分基本定理，定积分的计算，属于中档题14 （5 分）在ABC 中，A，B，C 的对边分别是 a，b，c，若c2acosB+bcosA，ab3，则ABC 的周长为 7 【分析】在ABC 中，利用余弦定理将 c2acos B+bcosA 中的 cosB 与 cosA 化为边之间的关系，化简整理可得 c1，从而可得ABC 的周长【解答】解：在ABC 中，c 2acos B+bcosA，由余弦定理得：c 2a +b c，c1 或 c0（舍） ，又 ab3，ABC 的周长为 3+3+17故答案为：7【点评】本题考查余弦定理及其应用，利用余弦定理将 c2acosB+

22、bcos A 中的 cosB 与cosA 化为边之间的关系是关键，考查转化思想与运算能力，属于中档题15 （5 分）从集合2，3，4 ，5 中随机抽取一个数 a，从集合 4，6，8中随机抽取一个数b，则向量 （a，b）与向量 （2，1）垂直的概率为    第 13 页（共 21 页）【分析】求得所有的（a，b）共有 12 个，满足 的（a，b）共有 3 个，由此求得向量 （a，b）与向量 （2，1）垂直的概率【解答】解：所有的（a，b）共有 4312 个，由向量 （a，b）与向量 （2，1）垂直，可得 2a+b0，故满足 的（a，b）共有 3 个：（2，4） 、 （3，6）

23、 ， （4，8） ，故向量 （a，b）与向量 （2，1）垂直的概率为 ，故答案为： 【点评】本题主要考查两个向量垂直的性质，古典概率及其计算公式，属于基础题16 （5 分）已知等腰直角ABC 的斜边 BC2，沿斜边的高线 AD 将ABC 折起，使二面角 BADC 为 ，则四面体 ABCD 的外接球的表面积为    【分析】由题意，BCD 是等边三角形，边长为 1，外接圆的半径为 ，AD1，可得四面体 ABCD 的外接球的半径 ，即可求出四面体 ABCD 的外接球的表面积【解答】解：由题意，BCD 是等边三角形，边长为 1，外接圆的半径为 ，AD1，四面体 ABCD 的外接球

24、的半径 ，四面体 ABCD 的外接球的表面积为 ，故答案为： 【点评】本题考查四面体 ABCD 的外接球的表面积，考查学生的计算能力，确定四面体ABCD 的外接球的半径是关键三、解答题：解答应写出文字说明、证明过程或演算步骤17 （12 分）设 Sn 是数列a n的前 n 项和，a n0，且 4Sna n（a n+2） （）求数列a n的通项公式；（）设 bn ，T nb 1+b2+bn，求证： Tn 【分析】 （I）利用数列递推关系即可得出（II）利用裂项求和、数列的单调性即可证明【解答】 （）解4S na n（a n+2） ，第 14 页（共 21 页）当 n1 时得 ，即 a12，当 n

25、2 时有 4Sn1 a n1 （a n1 +2）由 得 ，即 2（a n+an1 ）（a n+an1 ）（a na n1 ） ，又a n0，a na n1 2，a n2+2（n1）2n（）证明： ，T nb 1+b2+bn 【点评】本题考查了数列递推关系、裂项求和、数列的单调性，考查了推理能力与计算能力，属于中档题18 （12 分）医学上某种还没有完全攻克的疾病，治疗时需要通过药物控制其中的两项指标 H 和 V现有三种不同配方的药剂，根据分析， A，B，C 三种药剂能控制 H 指标的概率分别为 0.5，0.6，0.75，能控制 V 指标的概率分别是 0.6，0.5，0.4，能否控制 H 指标与

26、能否控制 V 指标之间相互没有影响（）求 A，B，C 三种药剂中恰有一种能控制 H 指标的概率；（）某种药剂能使两项指标 H 和 V 都得到控制就说该药剂有治疗效果求三种药剂中有治疗效果的药剂种数 X 的分布列【分析】 （）利用相互独立事件概率乘法公式、互斥事件概率加法公式能求出A，B，C 三种药剂中恰有一种能控制 H 指标的概率（）求出 A，B，C 三种药剂有治疗效果的概率均为 0.3，可看成是独立重复试验，即XB（3，0.3） ，由此能求出 X 的分布列【解答】解：（）A，B，C 三种药剂中恰有一种能控制 H 指标的概率为：0.5（10.6）（10.75）+（10.5）0.6（10.75）

27、+（10.5）（10.6）0.750.275（）A 有治疗效果的概率为 PA0.50.60.3，第 15 页（共 21 页）B 有治疗效果的概率为 PB0.60.50.3，C 有治疗效果的概率为 PC 0.750.40.3，A，B，C 三种药剂有治疗效果的概率均为 0.3，可看成是独立重复试验，即XB（3，0.3） ，X 的可能取得为 0，1，2，3， ，即 ，故 X 的分布列为：X 0 1 2 3P 0.343 0.441 0.189 0.027【点评】本题考查概率的求法，考查离散型随机变量的分布列，考查相互独立事件概率乘法公式、互斥事件概率加法公式、二项分布等基础知识，考查推理论证能力、运

28、算求解能力，考查函数与方程思想，是中档题19 （12 分）如图，棱柱 ABCDA 1B1C1D1 中，底面 ABCD 是平行四边形，侧棱 AA1底面 ABCD，AB 1，AC ，BC BB 12（）求证：AC平面 ABB1A1；（）求二面角 AC 1DC 的平面角的余弦值【分析】 （）推导出 ABAC，AA 1AC ，由此能证明 AC平面 ABB1A1（）过点 C 作 CPC 1D 于 P，连接 AP，则 AC平面 DCC1D1，从而CPA 是二面第 16 页（共 21 页）角 AC 1DC 的平面角，由此能求出二面角 AC 1DC 的平面角的余弦值【解答】证明：（）在底面 ABCD 中，AB

29、1，AC ，BC2，AB 2+AC2BC 2，ABAC ，侧棱 AA1底面 ABCD，AA 1AC，又AA 1ABA，AA 1，AB 平面 ABB1A1，AC平面 ABB1A1解：（）过点 C 作 CPC 1D 于 P，连接 AP，由（）可知，AC平面 DCC1D1，CPA 是二面角 AC 1DC 的平面角，CC 1BB 12，CDAB1，CP ，tan ，cos ，二面角 AC 1DC 的平面角的余弦值为 【点评】本题考查线面垂直的证明，考查二面角的余弦值的求法，是中档题，解题时要认真审题，注意空间思维能力的培养20 （12 分）已知椭圆 C： 1（a0）的焦点在 x 轴上，且椭圆 C 的焦

30、距为2（）求椭圆 C 的标准方程；（）过点 R（4，0）的直线 l 与椭圆 C 交于两点 P，Q，过 P 作 PNx 轴且与椭圆 C交于另一点 N，F 为椭圆 C 的右焦点，求证：三点 N，F，Q 在同一条直线上【分析】 （）由椭圆的焦点位置分析可得 a27a 2，进而由椭圆的几何性质可得a2（7a 2）1，解可得 a 的值，代入椭圆的方程即可得答案；（）分析可得直线 l 的斜率存在，设 l 的方程为 yk（x4） ，联立直线与椭圆的方程，第 17 页（共 21 页）由根与系数的关系分析可得直线 QN 方程，令 y0，可得直线 QN 过点（1，0） ，由椭圆的几何性质分析可得答案【解答】解：（

31、）椭圆 的焦点在 x 轴上，a 27a 2，即 ，椭圆 C 的焦距为 2，且 a2 b2c 2，a 2（7a 2）1，解得 a24，椭圆 C 的标准方程为 ；（）证明：由题知直线 l 的斜率存在，设 l 的方程为 yk（x4） ，点 P（x 1，y 1） ，Q （x 2，y 2） ，N（x 1，y 1） ，则 得 3x2+4k2（x 4） 212，即（3+4k 2）x 232k 2x+64k2120，0， ， ，由题可得直线 QN 方程为 ，又y 1k（x 1 4） ，y 2k（x 24） ，直线 QN 方程为 ，令 y0，整理得 ，即直线 QN 过点（1，0） ，又椭圆 C 的右焦点坐标为

32、F（1，0） ，三点 N，F，Q 在同一条直线上【点评】本题考查椭圆的几何性质，涉及直线与椭圆的位置关系，此类问题需要分析直第 18 页（共 21 页）线的斜率是否存在21 （12 分）已知函数 f（x ）（x 22x）1nx+ax 2+2，g（x）f（x）x2（）当 a1 时，求 f（x）在（1，f（1） ）处的切线方程；（）若 a0 且函数 g（x）有且仅有一个零点，求实数 a 的值；（）在（）的条件下，若 e2 xe 时，g（x）m 恒成立，求实数 m 的取值范围【分析】 （）当 a1 时，f'（x ）（2x2）1nx+（x2）2x，由此利用导数的几何意义能求出 f（x ）在（1

33、，f（1） ）处的切线方程（）令 g（x）f（x）x20，则 令 ，则h（x） ，令 t（x）1x21nx，则 ，由此利用导数性质能求出当函数 g（x）有且仅有一个零点时 a 的值（）当 a1，若 e2 x e ，g（x）m ，只需证明 g（x） maxm，由 g'（x）（x1） （3+21nx ） ，求出 是 g（x ）的极大值点，由此能求出实数 m 的取值范围【解答】解：（）当 a1 时，f（x ）（x 22x）1nxx 2+2 定义域（0，+） ，f'（x）（2x2）1nx+（x2）2x，f'（1）3，又 f（1）1，f（x）在（1 ，f（1） ）处的切线方程 3

34、x+y40（）令 g（x）f（x）x20，则（x 22x ）1nx+ax 2+2x +2即令 ，则 ，令 t（x）1 x21nx，则 ，x（0，+） ，t'（x）0，t（x）在（0 ，+）上是减函数，又t（1）h'（1）0，当 0x1 时，h'（x ）0，当 x1 时，h' （x ）0，第 19 页（共 21 页）h（x）在（0，1）上单调递增，在（1，+）上单调递减，h（x） maxh（1）10，又 ， ，a0当函数 g（x）有且仅有一个零点时，a1（）当 a1，g（x）（x 22x ）1nx+x 2x，若 e2 xe，g（x）m，只需证明 g（x） maxm

35、，g'（x）（x1） （3+21nx）令 g'（x ）0 得 x1 或 ，又e 2 xe，函数 g（x）在 上单调递增，在 上单调递减，在（1，e）上单调递增，即 是 g（x）的极大值点，又 ，g（e）2e 23e ， ，m 2e23e，实数 m 的取值范围是（2e 23e，+） 【点评】本题考查函数的切线方程、实数的取值范围、导数的几何意义、导数性质、构造法等基础知识，考查推理论证能力、运算求解能力，考查化归与转化思想、函数与方程思想，考查创新意识、应用意识，是中档题请考生在第 22、23 题中任选一题作答如果多做，则按所做的第一题记分.作答时用 2B 铅笔在答题卡上把所选题

36、目对应题号后的方框涂黑选修 4-4：坐标系与参数方程选讲22 （10 分）在平面直角坐标系 xoy 中，曲线 C 的参数方程为 （t 为参数） ，以 O为极点 x 轴的正半轴为极轴建极坐标系，直线 l 的极坐标方程为 （cos sin ）4，且与曲线 C 相交于 A，B 两点（）在直角坐标系下求曲线 C 与直线 l 的普通方程；（）求AOB 的面积第 20 页（共 21 页）【分析】 （）利用三种方程的转化方法，求曲线 C 与直线 l 的普通方程；（）求出|AB|，O 到直线 l 的距离，即可求AOB 的面积【解答】解：（）已知曲线 C 的参数方程为 （t 为参数） ，消去参数得y24x，直线

37、 l 的极坐标方程为 （cossin ）4，由 xcos ，y sin 得普通方程为xy40；（）已知抛物线 y24x 与直线 xy40 相交于 A， B 两点，由 ，得 ，O 到直线 l 的距离 ，所以AOB 的面积为 【点评】本题考查三种方程的转化，考查三角形面积的计算，属于中档题选修 4-5：不等式选讲23已知函数 f（x ）m|x1|， （m0） ，且 f（x+1） 0 的解集为3，3（）求 m 的值；（）若正实数 a，b，c 满足 ，求证：a+2b+3c3【分析】 （）f（x +1）0 等价于|x|m ，求出解集，利用 f（x+1）0 的解集为3，3，求 m 的值；（）由（）知 ，利用柯西不等式即可证明【解答】 （）解：因为 f（x+1）m|x |，所以 f（x+1）0 等价于|x|m ，由|x |m，得解集为m，m， （m0）又由 f（x+1）0 的解集为3，3，故 m3（）证明：由（）知 ，又a，b，c 是正实数，a+2b+3c 当且仅当 时等号成立，所以 a+2b+3c3第 21 页（共 21 页）【点评】本题考查不等式的解法，考查柯西不等式的运用，属于中档题