2019人教A版数学选修2-1学案（含解析）：1.1.2 四种命题1.1.3 四种命题间的相互关系

《2019人教A版数学选修2-1学案（含解析）：1.1.2 四种命题1.1.3 四种命题间的相互关系》由会员分享，可在线阅读，更多相关《2019人教A版数学选修2-1学案（含解析）：1.1.2 四种命题1.1.3 四种命题间的相互关系（11页珍藏版）》请在七七文库上搜索。

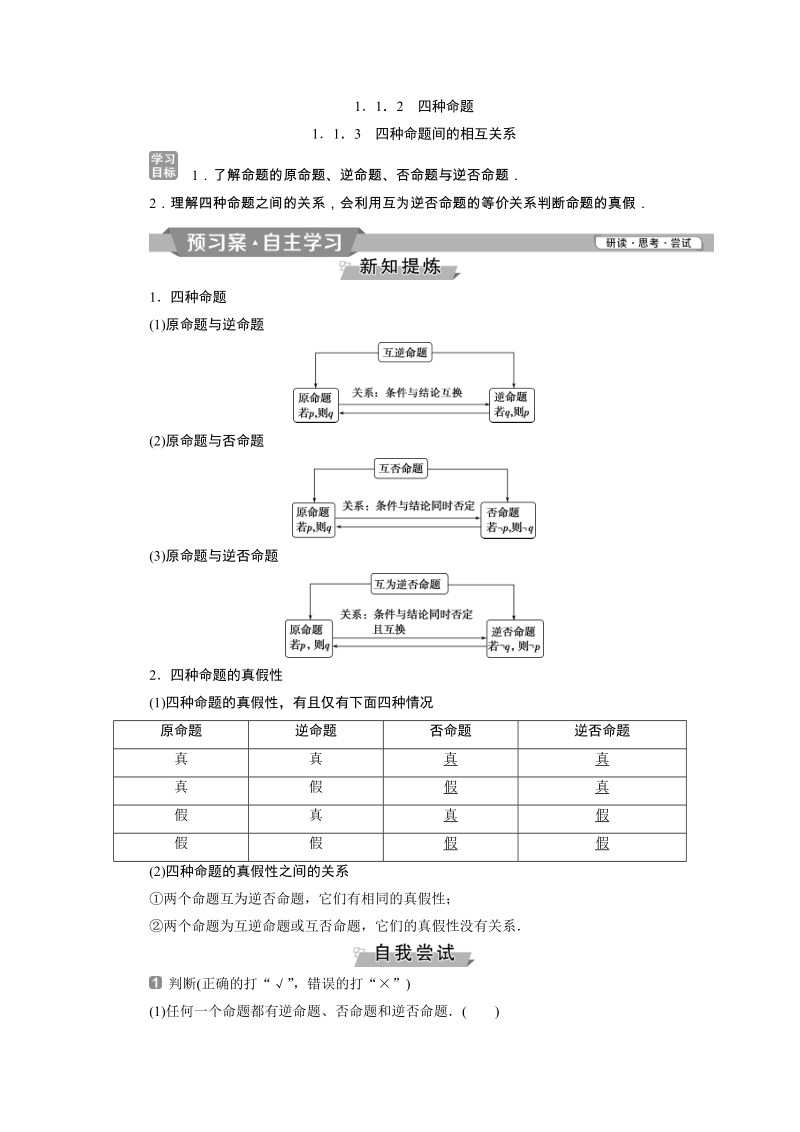
1、112 四种命题113 四种命题间的相互关系1了解命题的原命题、逆命题、否命题与逆否命题2理解四种命题之间的关系，会利用互为逆否命题的等价关系判断命题的真假1四种命题(1)原命题与逆命题(2)原命题与否命题(3)原命题与逆否命题2四种命题的真假性(1)四种命题的真假性，有且仅有下面四种情况原命题 逆命题 否命题 逆否命题真 真 真 真真 假 假 真假 真 真 假假 假 假 假(2)四种命题的真假性之间的关系两个命题互为逆否命题，它们有相同的真假性；两个命题为互逆命题或互否命题，它们的真假性没有关系判断(正确的打“” ，错误的打 “”)(1)任何一个命题都有逆命题、否命题和逆否命题( )(2)两

2、个互逆命题的真假性相同( )(3)对于一个命题的四种命题，可以一个真命题也没有( )答案：(1) (2) (3) “若 x21，则 x1”的否命题为( )A若 x21，则 x1 B若 x21，则 x1C若 x21，则 x1 D若 x1，则 x21答案：C命题“若一个数是负数，则它的平方是正数”的逆命题是( )A “若一个数是负数，则它的平方不是正数 ”B “若一个数的平方是正数，则它是负数”C “若一个数不是负数，则它的平方不是正数”D “若一个数的平方不是正数，则它不是负数 ”答案：B命题“若|a|b|，则 ab ”及其逆命题、否命题、逆否命题中，真命题的个数为 ( )A0 B1C2 D 4

3、解析：选 C原命题是假命题，则逆否命题也是假命题逆命题：若 ab，则|a| b|，是真命题，因此否命题也是真命题所以四个命题中真命题的个数为 2命题“若 a1，则 a0”的逆命题是_，逆否命题是_答案：若 a0，则 a1 若 a0，则 a1探究点 1 写原命题的其他三种命题把下列命题改写成“若 p，则 q”的形式，并写出它们的逆命题、否命题与逆否命题(1)全等三角形的对应边相等；(2)当 x2 时，x 23x 20 【解】 (1)原命题：若两个三角形全等，则这两个三角形三边对应相等；逆命题：若两个三角形三边对应相等，则这两个三角形全等；否命题：若两个三角形不全等，则这两个三角形三边对应不相等；

4、逆否命题：若两个三角形三边对应不相等，则这两个三角形不全等(2)原命题：若 x2，则 x23x20；逆命题：若 x23x 20，则 x2；否命题：若 x2，则 x23x 20；逆否命题：若 x23x 20，则 x2写出一个命题的其他三种命题的步骤(1)分析命题的条件和结论(2)将命题写成“若 p，则 q”的形式(3)根据逆命题、否命题、逆否命题各自的结构形式写出这三种命题注意 如果原命题含有大前提，在写出原命题的逆命题、否命题、逆否命题时，必须注意各命题中的大前提不变 1原命题“若 x3，则 x0”的逆否命题是( )A若 x3，则 x0 B若 x3，则 x0C若 x0，则 x3 D若 x0，则

5、 x3解析：选 C易知原命题的逆否命题是 “若 x0，则 x3” 2(2018山东济南外国语学校高二( 下)期中考试)设 a，b 是向量，命题“若 ab，则|a | b|”的逆命题是 ( )A若 ab，则|a| |b|B若 ab，则| a|b|C若|a| b|，则 abD若|a |b|，则 ab解析：选 D条件“ab” 和结论“|a|b| ”互换后得到逆命题：若|a| |b|，则ab故选 D探究点 2 四种命题的关系及真假判断下列命题：“若 xy1，则 x、y 互为倒数 ”的逆命题；“四边相等的四边形是正方形”的否命题；“梯形不是平行四边形”的逆否命题；“若 ac2bc 2，则 ab”的逆命题

6、其中是真命题的是_【解析】 “若 xy1，则 x，y 互为倒数”的逆命题是“若 x，y 互为倒数，则xy 1”，是真命题；“四边相等的四边形是正方形”的否命题是 “四边不都相等的四边形不是正方形” ，是真命题；“梯形不是平行四边形”本身是真命题，所以其逆否命题也是真命题；“若 ac2bc 2，则 ab”的逆命题是“若 ab，则 ac2bc 2”，是假命题，所以真命题是【答案】 (1)四种命题关系判断的两个要领在判断四种命题之间的关系时，首先要分清命题的条件和结论，再比较每个命题的条件和结论之间的关系原命题与逆否命题互为逆否命题，逆命题与否命题也互为逆否命题(2)判断四种命题真假的方法要正确理解

7、四种命题间的相互关系正确利用相关知识进行判断推理若由“p 经逻辑推理得出 q”，则命题“若 p，则 q”为真；确定“若 p，则 q”为假时，则只需举一个反例说明 分别写出下列命题的逆命题、否命题、逆否命题，并判断它们的真假(1)若 q ，则方程 x23xq0 有实根；94(2)若 ab0，则 a，b 中至少有一个为 0解：(1)逆命题：若方程 x23xq0 有实根，则 q 真命题94否命题：若 q ，则方程 x23xq0 无实根真命题94逆否命题：若方程 x23x q0 无实根，则 q 真命题94(2)逆命题：若 a，b 中至少有一个为 0，则 ab0真命题否命题：若 ab0，则 a，b 均不

8、为 0真命题逆否命题：若 a，b 均不为 0，则 ab0真命题探究点 3 等价命题的应用判断命题“已知 a，x 为实数，若关于 x 的不等式 x2(2 a1)xa 220 的解集是空集，则 a2”的真假【解】 原命题的逆否命题为“已知 a，x 为实数，若 a2，则关于 x 的不等式x2(2a 1) x a220 的解集不是空集” 判断真假如下：抛物线 yx 2(2a1)xa 22 的开口向上，判别式 (2a1) 24( a22)4a7，因为 a2，所以 4a70，即抛物线与 x 轴有交点，所以关于 x 的不等式 x2(2a1)xa 220 的解集不是空集，故原命题的逆否命题为真，从而原命题为真

9、等价命题的应用原则(1)在证明某一个命题的真假性有困难时，可以证明它的逆否命题为真( 假)命题，来间接地证明原命题为真(假)命题(2)四种命题中，原命题与其逆否命题是等价的，有相同的真假性，否命题与其逆命题也是互为逆否命题，解题时不要忽视 证明：已知函数 f(x)是(，) 上的增函数，a，bR，若 f(a)f(b)f( a) f(b)，则 ab0证明：原命题的逆否命题为“已知函数 f(x)是(，)上的增函数，a，bR，若ab ，则 ab”与它的逆命题、否命题、逆否命题这a b四个命题中，真命题的个数是( )A0 B1C2 D 4解析：选 C互为逆否的命题同真同假，原命题是真命题，故其逆否命题也

10、为真，逆命题为“已知 a，b 为实数，若 ab，则 ”，这个命题是假命题，故否命题也为假，从a b而有 2 个是真命题5(2018宝鸡高二检测)有下列四个命题：“若 xy0，则 x，y 互为相反数”的逆命题；“全等三角形的面积相等”的否命题；“若 q1，则 x22x q0 有实根”的逆否命题；“不等边三角形的三个内角相等”的逆命题其中真命题为( )A BC D 解析：选 C逆命题为“若 x，y 互为相反数，则 xy0” ，真命题；否命题为“不全等的三角形的面积不相等” ，假命题；当 q1 时，44q0，所以原命题是真命题，其逆否命题也是真命题；的逆命题为“三个内角相等的三角形是不等边三角形”

11、，假命题故选 C6(2018泉州高二检测)设 mR，命题“若 m0，则方程 x2x m0 有实根”的逆否命题是_ 解析：根据逆否命题的定义，命题“若 m0，则方程 x2 xm 0 有实根”的逆否命题是“若方程 x2x m0 没有实根，则 m0” 答案：若方程 x2x m0 没有实根，则 m07在命题“若数列a n是等比数列，则 an0”与它的逆命题、否命题、逆否命题中，真命题的个数为_解析：原命题为真命题，故其逆否命题为真命题，它的逆命题与否命题均为假命题答案：28给定下列命题：若 k0，则方程 x22x k0 有实数根；若 xy8，则 x2 或 y6；“矩形的对角线相等”的逆命题；“若 xy

12、0，则 x，y 中至少有一个为零 ”的否命题其中真命题的序号是_解析：中，当 k0 时， 2 24k44k0，故方程有实根，为真命题；中，其逆否命题为“若 x2 且 y6，则 xy8”为真，故原命题亦真；中，其逆命题为“若一个四边形的对角线相等，则这个四边形为矩形”为假命题；中，否命题为“若 xy0，则 x，y 全不为零”为真命题，故为真命题的序号是答案：9写出命题“若 x2y 20，则 x，y 全为 0”的逆命题、否命题和逆否命题，并判断它们的真假解：逆命题：若 x，y 全为 0，则 x2y 20，是真命题；否命题：若 x2y 20，则 x， y 不全为 0，是真命题；逆否命题：若 x，y

13、不全为 0，则 x2y 20，是真命题10已知命题 p：“若 ac0，则二次不等式 ax2bx c0 无解” (1)写出命题 p 的否命题；(2)判断命题 p 的否命题的真假解：(1)命题 p 的否命题为：“若 ac0，则二次不等式 ax2bxc0 有解” (2)命题 p 的否命题是真命题判断如下：因为 ac0，所以ac0 b 24ac 0二次方程 ax2bx c0 有两个不相等的实根ax2bxc0 有解，所以该命题是真命题B 能力提升11原命题为“若 a n，nN *，则 an为递减数列” ，关于其逆命题，否命an an 12题，逆否命题真假性的判断依次如下，正确的是( )A真，真，真 B假

14、，假，真C真，真，假 D假，假，假解析：选 A a nan1 a nan为递减数列原命题与其逆命题都是真an an 12命题，所以其逆否命题和否命题也都是真命题，故选 A12已知命题“若 m1xm 1，则 1x 2”的逆命题为真命题，则 m 的取值范围是_解析：由已知得，若 1x2 成立，则 m1xm1 也成立，所以 m 1 1，m 1 2，)所以 1m2答案：1，213主人邀请张三、李四、王五三个人吃饭，时间到了，只有张三、李四准时赴约，王五打电话说：“临时有急事，不能去了 ”主人听了，随口说了句：“该来的没有来 ”张三听了脸色一沉，起来一声不吭地走了主人愣了片刻，又道了句：“不该走的又走了

15、 ”李四听了大怒，拂袖而去请你用逻辑学原理解释二人离去的原因解：张三走的原因是：“该来的没有来”的逆否命题是“来了不该来的” ，张三觉得自己是不该来的李四走的原因是：“不该走的又走了”的逆否命题是“没走的应该走” ，李四觉得自己是应该走的14(选做题) 证明：若 a24b 22a10，则 a2b1证明：“若 a24b 22a10，则 a2b1”的逆否命题为“若 a2b1，则a24b 22a10” 因为 a2b1，所以 a24b 22a1(2b1) 24b 22(2 b1)14b 214b4b 24b210所以命题“若 a2b1，则 a24b 22a10”为真命题由原命题与逆否命题具有相同的真假性可知，结论正确