2019人教A版数学选修2-1学案（含解析）：3.1.2 空间向量的数乘运算

《2019人教A版数学选修2-1学案（含解析）：3.1.2 空间向量的数乘运算》由会员分享，可在线阅读，更多相关《2019人教A版数学选修2-1学案（含解析）：3.1.2 空间向量的数乘运算（18页珍藏版）》请在七七文库上搜索。

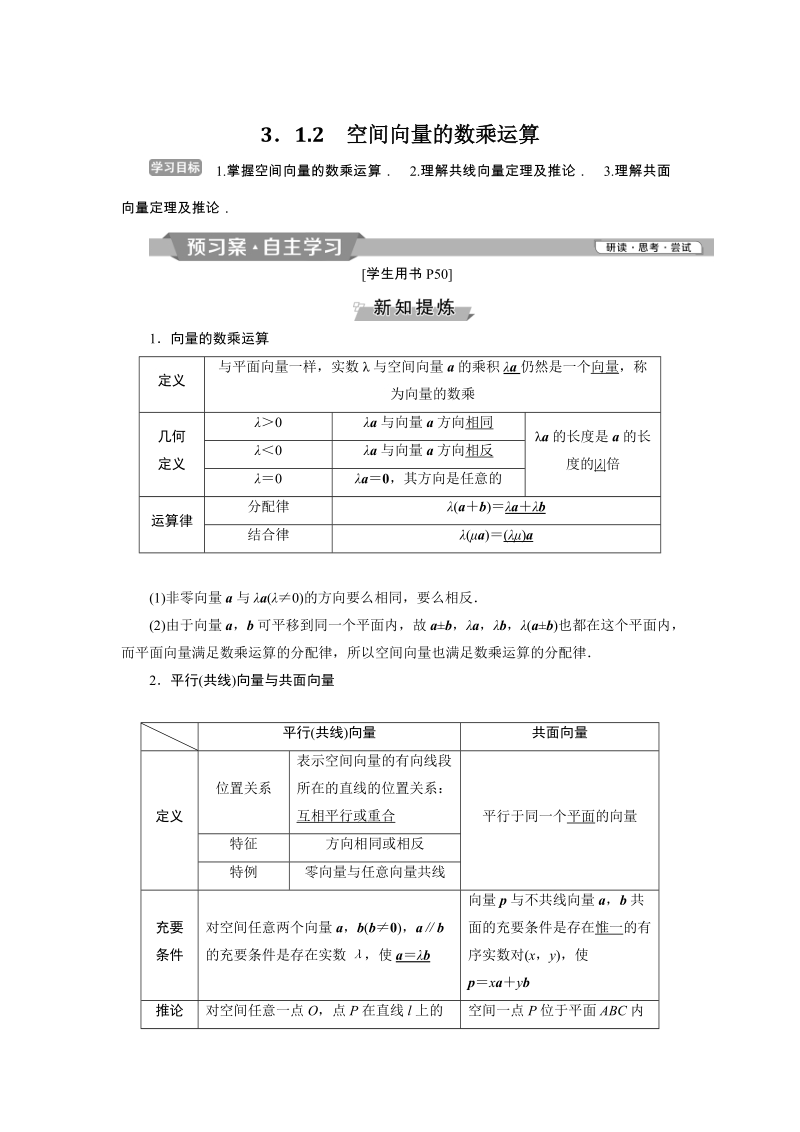
1、31.2 空间向量的数乘运算1.掌握空间向量的数乘运算 2.理解共线向量定理及推论 3.理解共面向量定理及推论学生用书 P501向量的数乘运算定义与平面向量一样，实数 与空间向量 a 的乘积 a 仍然是一个向量，称为向量的数乘0 a 与向量 a 方向相同0 a 与向量 a 方向相反几何定义0 a0，其方向是任意的a 的长度是 a 的长度的 |倍分配律 (ab) ab运算律结合律 (a)()a(1)非零向量 a 与 a(0)的方向要么相同，要么相反(2)由于向量 a，b 可平移到同一个平面内，故 ab，a， b，(ab)也都在这个平面内，而平面向量满足数乘运算的分配律，所以空间向量也满足数乘运算

2、的分配律 2平行(共线)向量与共面向量平行(共线) 向量 共面向量位置关系表示空间向量的有向线段所在的直线的位置关系：互相平行或重合特征 方向相同或相反定义特例 零向量与任意向量共线平行于同一个平面的向量充要条件对空间任意两个向量 a，b(b 0)，ab的充要条件是存在实数 ，使 ab向量 p 与不共线向量 a，b 共面的充要条件是存在惟一的有序实数对(x，y)，使pxayb推论 对空间任意一点 O，点 P 在直线 l 上的 空间一点 P 位于平面 ABC 内充要条件是存在实数 t 满足等式 ta，其中向量 a 为直线 l 的方OP OA 向向量或在直线 l 上取向量 a，则AB tOP OA

3、 AB 的充要条件是存在有序实数对(x，y)，使 x y 或AP AB AC 对空间任意一点 O，有 OP x yOA AB AC 判断(正确的打“” ，错误的打 “”)(1)实数与向量之间可进行加法、减法运算( )(2)若表示两向量的有向线段所在的直线为异面直线，则这两个向量不是共面向量( )(3)若 ab，则存在惟一的实数 ，使 ab.( )(4)空间中任意三个向量一定是共面向量( )答案：(1) (2) (3) (4)已知 R，则下列命题正确的是( )A|a|a| B| a| |aC|a| |a| D.|a|0答案：C若 e1，e 2 不共线，则下列各组中的两个向量 a，b 共线的是 (

4、 )Aae 1e 2，b e1 e212 12Ba e1 e2，b2e 13e 212 13Ca e1 e2，b2e 13e 213 12Dae 1e 2，b e1 e212 12答案：C空间的任意三个向量 a， b，3a2b，它们一定是( )A共线向量 B共面向量C不共面向量 D.既不共线也不共面向量答案：B3a2b (a4b)_12答案： a4b52探究点 1 空间向量的数乘运算学生用书 P51如图，在平行六面体 ABCDA1B1C1D1 中，设a， b， c，M ，N，P 分别是 AA1，BC ，C 1D1 的中点，AA1 AB AD 试用 a，b，c 表示以下各向量：(1) ；(2)

5、；(3) .AP A1N MP NC1 【解】 (1)因为 P 是 C1D1 的中点，所以 a AP AA1 A1D1 D1P AD 12D1C1 ac ac b.12AB 12(2)因为 N 是 BC 的中点，所以 abA1N A1A AB BN 12BC ab ab c.12AD 12(3)因为 M 是 AA1 的中点，所以 MP MA AP 12A1A AP a(ac b) a bc .12 12 12 12又 NC1 NC CC1 12BC AA1 ca，12AD AA1 12所以 MP NC1 (12a 12b c) (a 12c) a b c.32 12 321.变条件 若将本例中

6、“P 为 C1D1 的中点”改为“P 在线段 C1D1 上，且 ”，其C1PPD1 12他条件不变，如何用 a，b，c 表示 ？AP 解：因为 ，C1PPD1 12所以 .C1P 13C1D1 所以 AP AB BC CC1 C1P AB AD AA1 13C1D1 AB AD AA1 13AB ，即 a bc.23AB AD AA1 AP 232变条件 本例中若 O 是 B1D1 的中点，其他条件不变，如何用 a，b，c 表示 ？AO 解：因为 O 为 B1D1 的中点所以 AO 12AB1 12AD1 ( ) ( )12AA1 AB 12AA1 AD AA1 12AB 12AD a b c

7、. 12 12利用数乘运算进行向量表示的技巧(1)数形结合：利用数乘运算解题时，要结合具体图形，利用三角形法则、平行四边形法则，将目标向量转化为已知向量(2)明确目标：在化简过程中要有目标意识，巧妙利用中点坐标公式 在空间四边形 ABCD 中，G 为BCD 的重心，E，F，H 分别为边CD，AD 和 BC 的中点，化简下列各表达式(1) ；AG 13BE 12CA (2) ( )12AB AC AD 解：(1)因为 G 是BCD 的重心，所以| | | |，GE 13BE 所以 .13BE GE 又因为 ，12CA EF 所以由向量的加法法则，可知 ， .AG 13BE AG GE AE AE

8、 12CA AE EF AF 从而 .AG 13BE 12CA AF (2)如图所示，分别取 AB，AC 的中点 P，Q ，连接 PH，QH，则四边形 APHQ 为平行四边形，且有 ， ，而 ， 12AB AP 12AC AQ AP AQ AH 12AD ，AF 所以 ( ) .12AB AC AD AP AQ AF AH AF FH 探究点 2 空间向量的共线问题学生用书 P52如图，在平行六面体 ABCDA1B1C1D1 中，M ，N 分别是C1D1， AB 的中点，E 在 AA1 上且 AE2EA 1，F 在 CC1 上且CF FC1，判断 与 是否共线12 ME NF 【解】 由已知可

9、得， ME MD1 D1A1 A1E 12BA CB 13A1A NB CB 13C1C CN FC .FN NF 所以 ，ME NF 故 与 共线ME NF 变条件 在本例中，若 M、N 分别为 AD1，BD 的中点，证明 与 共线MN D1C 证明：连接 AC，则 NAC 且 N 为 AC 的中点，所以 ，由已知得 ，AN 12AC AM 12AD1 所以 MN AN AM .12AC 12AD1 12D1C 所以 与 共线MN D1C (1)判断向量共线的方法判断向量共线就是充分利用已知条件找到实数 ，使 ab( b0)成立，同时要充分运用空间向量的运算法则，结合空间图形，化简得出 ab

10、( b0) ，从而得出 ab.(2)证明空间三点共线的三种思路对于空间三点 P，A，B 可通过证明下列结论来证明三点共线存在实数 ，使 成立；PA PB 对空间任一点 O，有 t (tR)；OP OA AB 对空间任一点 O，有 x y (xy1) OP OA OB 1.已知非零向量 e1、e 2 不共线，则使 ke1e 2 与 e1ke 2 共线的 k 的值是_解析：若 ke1e 2 与 e1ke 2 共线，则 ke1e 2(e 1ke 2)，所以 k ，k 1.)所以 k1.答案：12.如图所示，在正方体 ABCDA1B1C1D1 中，E 在 A1D1 上，且2 ，F 在对角线 A1C 上

11、，且 .求证：E，F，B 三A1E ED1 A1F 23FC 点共线证明：设 a， b， c.AB AD AA1 因为 2 ， ，A1E ED1 A1F 23FC 所以 ， .A1E 23A1D1 A1F 25A1C 所以 b，A1E 23AD 23 ( )A1F 25AC AA1 ( )25AB AD AA1 a b c.25 25 25所以 a b cEF A1F A1E 25 415 25 (a bc)25 23又 EB EA1 A1A AB bcaa bc ，23 23所以 ，EF 25EB 所以 E，F ，B 三点共线探究点 3 空间向量的共面问题学生用书 P53如图所示，已知矩形

12、ABCD 和矩形 ADEF 所在的平面互相垂直，点 M，N 分别在对角线 BD，AE 上，且 BM BD，AN AE.求证：向量 ， ， 共面13 13 MN CD DE 【证明】 因为 M 在 BD 上，且 BM BD，13所以 .MB 13DB 13DA 13AB 同理 .AN 13AD 13DE 所以 MN MB BA AN (13DA 13AB ) BA (13AD 13DE ) .23BA 13DE 23CD 13DE 又 与 不共线，根据向量共面的充要条件可知 ， ， 共面CD DE MN CD DE 证明空间三向量共面或四点共面的方法(1)向量表示：设法证明其中一个向量可以表示成

13、另两个向量的线性组合，即若pxayb，则向量 p，a，b 共面(2)若存在有序实数组(x ，y，z) 使得对于空间任一点 O，有 x y z ，且OP OA OB OC xyz 1 成立，则 P，A， B，C 四点共面 已知非零向量 e1，e 2 不共线，如果 e1 e2， 2e 18e 2， 3e 13e 2，求证：A，B，C，D 四点共面AB AC AD 证明：令 x y ，则 e1e 2x(2e 18e 2)y(3e 13e 2)(2x3y)e 1(8x3y)e 2.AB AC AD 因为 e1 和 e2 不共线，所以 2x 3y 1，8x 3y 1，)解得x 15，y 15.)所以 ，

14、AB 15AC 15AD 所以 A，B ，C，D 四点共面1已知两非零向量 e1，e 2，且 e1 与 e2 不共线，设 ae 1e 2(，R，且 2 20) ，则( )Aae 1Bae 2Ca 与 e1、e 2 共面D以上三种情况均有可能解析：选 C.假设 a 与 e1 共线，则 ake 1，所以 ae 1e 2 可变为( k)e 1e 2，所以e1 与 e2 共线，这与 e1 与 e2 不共线相矛盾，故假设不成立，则 A 不正确，同理 B 不正确，则 D 也错误2在平行六面体 ABCDEFGH 中，若 x 2y 3z ，则 xyz 等于( )AG AB BC DH A. B.76 23C.

15、 D.56 34解析：选 C.由于 ，对照已知式子可得AG AB AD CG AB BC DH x1，2y1，3z1，故 x1，y ，z ，12 13从而 xyz .563有下列命题：若 ，则 A，B ，C ，D 四点共线；若 ，则 A，B，C 三点共线；AB CD AB AC 若 e1，e 2 为不共线的非零向量， a4e 1e 2，be 1 e2，则 ab；14其中真命题是_(把所有真命题的序号都填上 )解析：根据共线向量的定义，知若 ，则 ABCD 或 A，B，C，D 四点共线，AB CD 故是假命题；若 且 ， 有公共点 A，则 A，B，C 三点共线，所以是真命题；AB AC AB A

16、C 由于 a4e 1e 24 4b，所以 ab，故是真命题( e1 14e2)答案：4在正方体 ABCDA1B1C1D1 中，E 是上底面 A1C1 的中心，化简下列向量表达式，并在图中标出化简后的向量(1) ；AB BC CC1 (2) .AA1 12AB 12AD 解：(1) .AB BC CC1 AC1 (2) ( ) ( )AA1 12AB 12AD AA1 12AB AD AA1 12D1C1 A1D1 .AA1 12A1C1 AA1 A1E AE 向量 ， 如图所示AC1 AE 学生用书 P54知识结构 深化拓展两个定理的再认识(1)直线的方向向量是指与直线平行或共线的向量一条直线

17、的方向向量有无限多个，它们的方向相同或相反(2)证明(或判断 )三点 A，B，C 共线时，只需证明存在实数 ，使 (或 )即可；也可用“对空间任意一点 O，有AB BC AB AC t (1t) ”来证明三点共线OC OA OB (3)共面向量的充要条件给出了平面的向量表示式，说明空间中任意一个平面都可以由两个不共线的平面向量表示出来(4)空间一点 P 位于平面 MAB 内的充分必要条件是存在有序实数对(x， y)，使 x y .满足这个关系式的点 P 都在平MP MA MB 面 MAB 内；反之，平面 MAB 内的任一点 P 都满足这个关系式. 学生用书 P129(单独成册 )A 基础达标1

18、已知空间四边形 ABCD 中，G 为 CD 的中点，则 ( )等于( )AB 12BD BC A. B.AG CG C. D.BC 12BC 解析：选 A. ( ) (2 ) .AB 12BD BC AB 12 BG AB BG AG 2设 a，b 是不共线的两个向量，R ，且 ab0，则( )A 0 Bab0C0，b0 D.0，a0解析：选 A.因为 a，b 不共线，所以 a，b 均为非零向量，又因为 ab0，所以 0.3已知向量 a，b，且 a2b， 5a6b， 7a2b，则一定共线的三点AB BC CD 是( )AA、B 、D BA、B、CCB、C、D D.A、C 、D解析：选 A.因为

19、 a2b.AB 2a4b2(a 2b) 2 ，BD BC CD AB 所以 ，由于 与 有一个公共点 B，AB BD AB BD 所以 A、B 、D 三点共线4在下列条件中，使 M 与 A，B，C 一定共面的是( )A. 3 2 OM OA OB OC B. 0OM OA OB OC C. 0MA MB MC D. OM 14OB OA 12OC 解析：选 C.因为 0，MA MB MC 所以 ，所以 M 与 A，B ，C 必共面MA MB MC 5给出下列命题：若 A，B，C，D 是空间任意四点，则有 0；AB BC CD DA |a |b| a b|是 a，b 共线的充要条件；若 ， 共线

20、，则 ABCD；AB CD 对空间任意一点 O 与不共线的三点 A，B，C，若 x y z (其中OP OA OB OC x，y，z R)，则 P，A，B ，C 四点共面其中不正确命题的个数是( )A1 B2 C3 D4解析：选 C.显然正确；若 a，b 共线，则| a|b| |ab|或| ab|a|b|，故错误；若 ， 共线，则直线 AB， CD 可能重合，故错误；只有当 xyz1 时，AB CD P，A ，B ，C 四点才共面，故错误故选 C.6化简： (a2b3c)5( a b c)3(a2bc) _12 23 12 23解析：原式( 5 3)a( 25 32) b(3 5 3)12 2

21、3 12 12 12 23c a b c.56 92 76答案： a b c56 92 767在三棱锥 ABCD 中，若 BCD 是正三角形，E 为其中心，则化简 的结果为_AB 12BC 32DE AD 解析：如图，延长 DE 交边 BC 于点 F，则 ， ，故AB 12BC AF 32DE AD AD DF AF 0.AB 12BC 32DE AD 答案：08已知 A，B ，C 三点共线，则对空间任一点 O，存在三个不为 0 的实数 ，m，n，使 m n 0，那么 m n 的值为_ OA OB OC 解析：因为 A，B，C 三点共线，所以存在惟一实数 k 使 k ，AB AC 即 k( )

22、，OB OA OC OA 所以(k 1) k 0.OA OB OC 又 m n 0，OA OB OC 令 k1，m1，nk ，则 mn0.答案：09.如图，设 O 为ABCD 所在平面外任意一点， E 为 OC 的中点，若 x yAE 12OD OB ，求 x，y 的值OA 解：因为 AE AB BC CE OB OA OC OB 12OC OA 12OC ( )OA 12OD DC ( )OA 12OD AB ( )OA 12OD 12OB OA ，32OA 12OD 12OB 所以 x ，y .12 3210在正方体 ABCDA1B1C1D1 中，M ，N ，P，Q 分别为 A1D1，D

23、1C1，AA 1，CC 1 的中点，求证：M，N，P，Q 四点共面证明：令 a， b， c.D1A1 D1C1 D1D 因为 M，N，P，Q 均为棱的中点，所以 b a， a c， ab c.MN 12 12 MP MA1 A1P 12 12 MQ MD1 D1C1 C1Q 12 12令 ，则 ab c () a b c，MQ MN MP 12 12 12 12 12所以12（ ） 12，12 1，12 12. )解得 2， 1.)所以 2 ，MQ MN MP 所以向量 ， ， 共面，MQ MN MP 所以 M，N，P，Q 四点共面B 能力提升11对于空间一点 O 和不共线的三点 A，B，C，

24、有 6 2 3 ，则( )OP OA OB OC AO，A，B ，C 四点共面BP，A，B ， C 四点共面CO，P，B，C 四点共面DO，P，A ，B ，C 五点共面解析：选 B.由 6 2 3 ，OP OA OB OC 得 2( )3( )，OP OA OB OP OC OP 即 2 3 ，AP PB PC 故 ， ， 共面，又它们有公共点 P，AP PB PC 因此，P，A ，B ，C 四点共面12已知 A，B，C 三点不共线，O 是平面 ABC 外任意一点，若由 OP 15OA 23OB 确定的一点 P 与 A，B，C 三点共面，则 _OC 解析：根据 P，A，B ，C 四点共面的条件

25、，知存在实数 x，y，z，使得x y z 成立，其中 xy z 1，于是 1，所以 .OP OA OB OC 15 23 215答案：21513已知 A，B，C 三点不共线，另外一点 M 满足 .OM 13OA 13OB 13OC (1)判断 ， ， 三个向量是否共面；MA MB MC (2)判断 M 是否在平面 ABC 内解：(1)因为 3 ，OA OB OC OM 所以 ( )( ) .OA OM OM OB OM OC BM CM 所以 .MA BM CM MB MC 所以向量 ， ， 共面MA MB MC (2)由(1)知向量 ， ， 共面，而它们有共同的起点 M，且 A，B，C 三点

26、不共线，MA MB MC 所以 M，A ，B，C 共面，即 M 在平面 ABC 内14.(选做题) 如图，已知 OE 是平行六面体 OADBCFEG 的体对角线，点 M 是ABC 的重心，求证：点 M 在直线 OE 上证明：如图，连接 AM 并延长交 BC 于点 H，因为 M 是ABC 的重心，所以 H 为 BC 的中点，所以 ( )AH 12AB AC 所以 AM 23AH ( )13AB AC ( )( )13 OB OA OC OA .13OB 13OC 23OA 所以 ( )OM OA AM 13OA OB OC 又因为 ，OE OA AD DE OA OB OC 所以 ，所以点 M 在直线 OE 上OM 13OE