6.4（第4课时）利用三边证相似 同步分层训练（含答案）

《6.4（第4课时）利用三边证相似 同步分层训练（含答案）》由会员分享，可在线阅读，更多相关《6.4（第4课时）利用三边证相似 同步分层训练（含答案）（8页珍藏版）》请在七七文库上搜索。

1、第4课时利用三边证相似知识点 1判定两个三角形相似1.如图6-4-43,在44的正方形网格中各有一个三角形,其中与图中的三角形相似的是 ()图6-4-43A. B.C.和 D.和2.在ABC中,ABBCCA=234,在ABC中,AB=1,CA=2,当BC=时,ABCABC.3.如图6-4-44,在ABC和DEF中,已知ABDE=BCEF,再添加一个条件:,可使ABCDEF.图6-4-444.已知一个三角形的三边长分别是6 cm,7.5 cm,9 cm,另一个三角形的三边长分别是8 cm,10 cm,12 cm,则这两个三角形(填“相似”或“不相似”).5.根据下列条件,判断ABC与ABC是否相

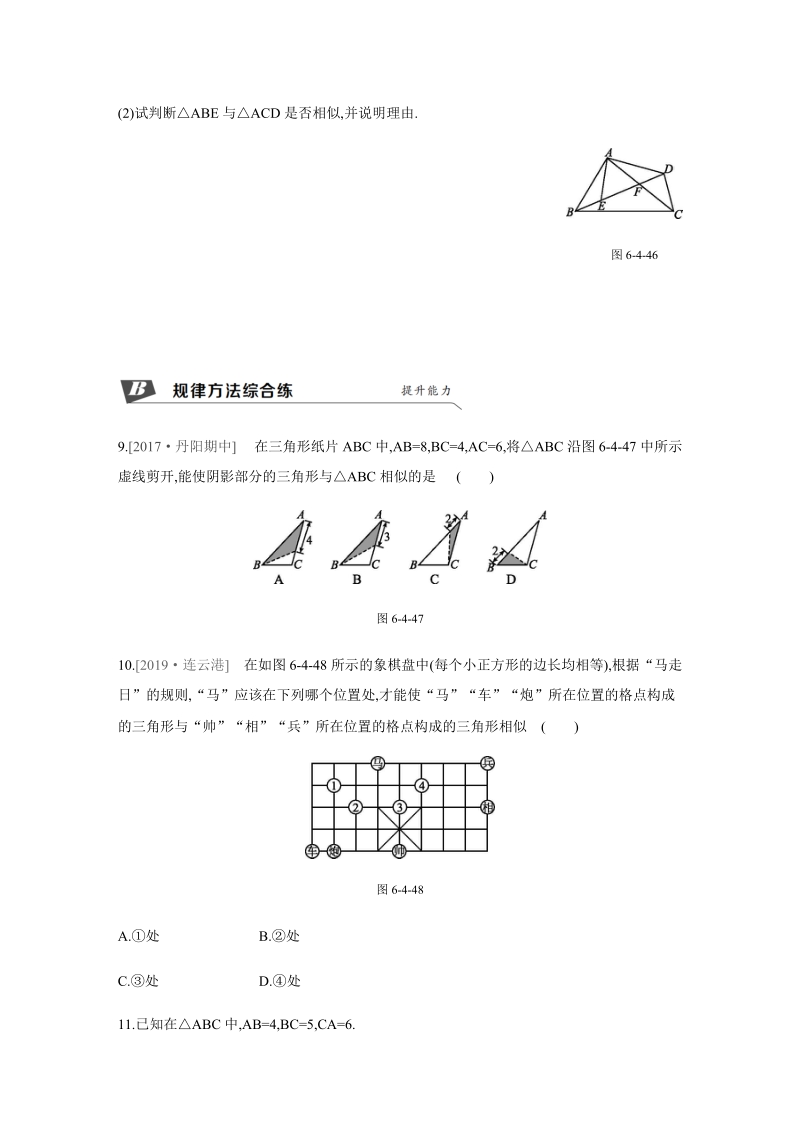
2、似,并说明理由.(1)A=80,AB=10,AC=20,A=80,AB=4,AC=6;(2)AB=5,BC=6,AC=7,AB=15,BC=18,AC=21.6.如图6-4-45,网格中每个方格都是边长为1的小正方形.若A,B,C,D,E,F都是小正方形的格点.求证:ABCDEF.图6-4-45知识点 2判定两个三角形相似的运用7.若ABC的每条边长都增加各自的10%得到ABC,则B的度数与其对应角B的度数相比()A.增加了10% B.减少了10%C.增加了(1+10%) D.没有改变8.教材练习第3题变式 2018建湖县一模 如图6-4-46,在四边形ABCD中,AC,BD相交于点F,点E在

3、BD上,且ABAE=BCED=ACAD.(1)BAE与CAD相等吗?为什么?(2)试判断ABE与ACD是否相似,并说明理由.图6-4-469.2017丹阳期中 在三角形纸片ABC中,AB=8,BC=4,AC=6,将ABC沿图6-4-47中所示虚线剪开,能使阴影部分的三角形与ABC相似的是()图6-4-4710.2019连云港 在如图6-4-48所示的象棋盘中(每个小正方形的边长均相等),根据“马走日”的规则,“马”应该在下列哪个位置处,才能使“马”“车”“炮”所在位置的格点构成的三角形与“帅”“相”“兵”所在位置的格点构成的三角形相似()图6-4-48A.处 B.处C.处 D.处11.已知在A

4、BC中,AB=4,BC=5,CA=6.(1)如果DE=10,那么当EF=,FD=时,DEFABC;(2)如果DE=10,那么当EF=,FD=时,FDEABC.12.如图6-4-49,O是ABC内一点,D,E,F分别为OA,OB,OC上的点,且ODOA=OEOB=OFOC.求证:DEFABC.图6-4-4913.已知:如图6-4-50,在RtABC和RtABC中,C=C=90,ABAB=ACAC.求证:RtABCRtABC.图6-4-5014.如图6-4-51,方格纸中每个小正方形的边长均为1,ABC和DEF的顶点都在方格纸的格点上.(1)判断ABC和DEF是否相似,并说明理由;(2)P1,P2

5、,P3,P4,P5,D,F是DEF边上的7个格点,请在这7个格点中选取3个点作为三角形的顶点,使构成的三角形与ABC相似.(要求写出2个符合条件的三角形,并在图中连接相应的线段,不必说明理由)图6-4-51教师详解详析1.A解析 已知图中的三角形的三条边长分别是2,22,25.图中三角形的三条边长分别是2,2,10;图中三角形的三条边长分别是3,2,5;图中三角形的三条边长分别是3,17,42.只有图中的三角形的三条边与图中的三角形的三条边对应成比例:222=22=1025=22.故选A.2.1.5解析 要使ABCABC,就需要ABBCCA=ABBCCA,从而求得BC=1.5.3.答案不唯一,

6、如B=E,ABDE=ACDF等4.相似5.解:(1)不相似.因为ABAB=104=52,ACAC=206=103,所以ABABACAC,所以ABC与ABC不相似.(2)相似.因为ABAB=515=13,BCBC=618=13,ACAC=721=13,所以ABAB=BCBC=ACAC.因为ABC与ABC的三条边对应成比例,所以ABCABC.6.证明:由图示及勾股定理,得AC=2,BC=10,AB=4,DF=22,EF=210,DE=8,ACDF=BCEF=ABDE=12,ABCDEF.7.D解析 AB=1.1AB,AC=1.1AC,BC=1.1BC,ABAB=ACAC=BCBC=1.1,ABCA

7、BC,B=B.故选D.8.解:(1)BAE与CAD相等.理由:ABAE=BCED=ACAD,ABCAED,BAC=EAD,BAE=CAD.(2)ABE与ACD相似.理由:ABAE=ACAD,ABAC=AEAD.又BAE=CAD,ABEACD.9.D解析 在三角形纸片ABC中,AB=8,BC=4,AC=6.A项,4AB=48=12,对应边ACAB=68=3412,沿虚线剪下的阴影三角形与ABC不相似,故此选项错误;B项,3AB=38,对应边ACAB=68=3438,沿虚线剪下的阴影三角形与ABC不相似,故此选项错误;C项,2AC=26=13,对应边ACAB=68=3413,沿虚线剪下的阴影三角形

8、与ABC不相似,故此选项错误;D项,2BC=24=12,对应边BCAB=48=12,B=B,沿虚线剪下的阴影三角形与ABC相似,故此选项正确.故选D.10.B解析 设小正方形的边长为1,则“帅”“相”“兵”所在位置的格点构成的三角形的三边的长分别为2,25,42,“车”“炮”之间的距离为1,“炮”与之间的距离为5,“车”与之间的距离为22.525=2242=12,“马”应该落在的位置处.故选B.11.(1)25215(2)128解析 本题考查相似三角形顶点和边的对应关系.DEFABC意味着DEAB=EFBC=FDCA,FDEABC意味着FDAB=DEBC=EFCA.12.证明:ODOA=OEO

9、B,DOE=AOB,ODEOAB,ODOA=DEAB.同理ODOA=DFAC,OEOB=EFBC.ODOA=OEOB,DEAB=DFAC=EFBC,DEFABC.13.证明:设ABAB=ACAC=k(k0),则AB=kAB,AC=kAC.在RtABC和RtABC中,BCBC=AB2-AC2AB2-AC2=k2AB2-k2AC2AB2-AC2=k,ABAB=ACAC=BCBC,RtABCRtABC.14.解析 要判断两个三角形是否相似,要么找到两个角相等,要么说明两边对应成比例及其夹角相等,要么说明各对应边的比值相等.作一个三角形与已知三角形相似也用同样的办法.解:(1)ABC和DEF相似.理由:根据勾股定理,得AB=25,AC=5,BC=5;DE=42,DF=22,EF=210.ABDE=ACDF=BCEF=522,ABCDEF.(2)答案不唯一,下面6个三角形中的任意2个均可,如图.P2P5D,P4P5F,P2P4D,P4P5D,P2P4P5,P1FD.