第三十二章 投影与视图自我综合评价（四）含答案

《第三十二章 投影与视图自我综合评价（四）含答案》由会员分享，可在线阅读，更多相关《第三十二章 投影与视图自我综合评价（四）含答案（8页珍藏版）》请在七七文库上搜索。

1、自我综合评价(四)范围:第三十二章投影与视图时间:40分钟分值:100分一、选择题(每小题5分,共30分)1.下列图形中,表示同一地点的两棵小树在同一时刻阳光下的影子可能是()图32-Z-12.把一个正五棱柱如图32-Z-2摆放,当投射光线由正前方射到后方时,它的正投影大致是() 图32-Z-2 图32-Z-3 3.图32-Z-4是一个L形状的物体,则它的俯视图是() 图32-Z-4 图32-Z-5 4.在图32-Z-6上剪去中的一个图形,剩下的图形可以折叠成一个长方体,则剪去的这个图形是()A. B. C. D. 图32-Z-6 图32-Z-75.图32-Z-7是一个几何体的三视图,其中主视

2、图与左视图完全一样,则这个几何体的表面积是()A.80-2 B.80+4C.80 D.80+66.如图32-Z-8,圆柱的底面周长为6 cm,AC是底面圆的直径,高BC为6 cm,P是母线BC上一点,且PC=23BC.一只蚂蚁从点A出发沿着圆柱的表面爬行到点P的最短路程是()图32-Z-8A.4+6cm B.5 cmC.35 cm D.7 cm二、填空题(每小题5分,共30分)7.如图32-Z-9,同一时刻在阳光的照射下,树AB的影子BC=3 m,小明的影子BC=1.5 m,已知小明的身高AB=1.7 m,则树高 AB=. 图32-Z-9 图32-Z-108.如图32-Z-10,小芸用灯泡O照

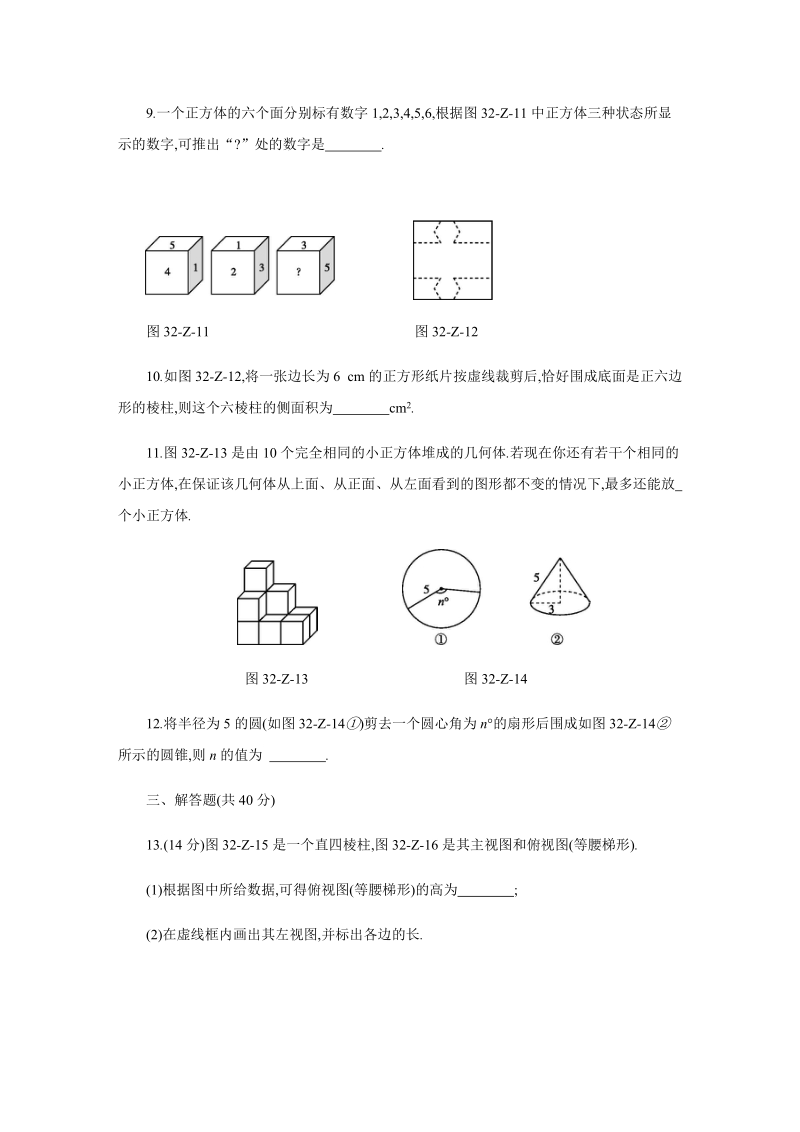
3、射一个矩形相框ABCD,在墙上形成影子ABCD.现测得OA=20 cm,OA=50 cm,相框ABCD的面积为80 cm2,则影子ABCD的面积为 cm2.9.一个正方体的六个面分别标有数字1,2,3,4,5,6,根据图32-Z-11中正方体三种状态所显示的数字,可推出“?”处的数字是. 图32-Z-11 图32-Z-1210.如图32-Z-12,将一张边长为6 cm的正方形纸片按虚线裁剪后,恰好围成底面是正六边形的棱柱,则这个六棱柱的侧面积为cm2.11.图32-Z-13是由10个完全相同的小正方体堆成的几何体.若现在你还有若干个相同的小正方体,在保证该几何体从上面、从正面、从左面看到的图形

4、都不变的情况下,最多还能放个小正方体. 图32-Z-13 图32-Z-1412.将半径为5的圆(如图32-Z-14)剪去一个圆心角为n的扇形后围成如图32-Z-14所示的圆锥,则n的值为 .三、解答题(共40分)13.(14分)图32-Z-15是一个直四棱柱,图32-Z-16是其主视图和俯视图(等腰梯形).(1)根据图中所给数据,可得俯视图(等腰梯形)的高为;(2)在虚线框内画出其左视图,并标出各边的长. 图32-Z-15 图32-Z-1614.(14分)按要求作图.(1)在图32-Z-17中画出同一时刻在阳光下旗杆的影子;(2)在图32-Z-17中确定路灯灯泡的位置,并画出小周在灯光下的影子

5、. 图32-Z-1715.(12分)如图32-Z-18所示,在一面与地面垂直的墙面的同一侧有一根高10米的旗杆AB和一个高度未知的电线杆CD.它们都与地面垂直.为了测得电线杆的高度,一个小组的同学进行了如下测量:某一时刻,在太阳光的照射下,旗杆落在墙面上的影子EF的长度为2米,落在地面上的影子BF的长度为10米;而电线杆落在围墙上的影子GH的长度为3米,落在地面上的影子DH的长度为5米.依据这些数据,该小组的同学计算出了电线杆的高度.(1)该小组的同学在这里利用的是投影的有关知识进行计算的;(2)试计算出电线杆的高度,并写出计算过程.图32-Z-18教师详解详析【作者说卷】本章是初中数学知识的

6、最后一章,学好本章知识可以解决生活中的许多与视图、投影有关的实际问题,同时为下一阶段的学习打下基础并做好准备.学习投影与视图知识可以把生活中的平面图形,如简单的模型图、平面图、地图、照片等与数学知识联系和统一起来,用数学化的知识来描述形形色色的图形.本套试题在考查基础知识、基本技能的同时,考查转化思想(空间问题平面化,曲折问题平直化)、整体与局部思想、数学建模思想、分类讨论思想等数学思想方法的运用.1.A解析 A项,影子的方向相同,且较高的树的影子长度大于较低的树的影子,故本选项符合题意;B项,影子的方向不相同,故本选项不符合题意;C项,影子的方向不相同,故本选项不符合题意;D项,树高与影子是

7、成正比的,较高的树的影子长度应大于较低的树的影子,故本选项不符合题意.故选A.2.B3.B解析 从上面看可得到两个左右相邻的长方形,并且左边的长方形的宽度远小于右边的长方形的宽度.4.A5.B解析 由三视图可知,该几何体是长方体,中间是空心圆柱,长方体的长、宽、高分别为4,4,3,圆柱直径为2,高为3,则长方体表面积为442+434=80,圆柱侧面积为23=6,上、下表面空心圆的面积和为2,这个几何体的表面积是80+6-2=80+4.6.B解析首先画出圆柱的侧面展开图,根据高BC=6 cm,PC=23BC,求出PC=236=4(cm).在RtACP中,根据勾股定理求出AP的长即可.具体的解答过

8、程如下:侧面展开图如图所示,圆柱的底面周长为6 cm,AC=3 cm.PC=23BC,PC=236=4(cm).在RtACP中,AP2=AC2+PC2,AP=32+42=5(cm).故选B.7.3.4 m解析 根据题意得ABBC=ABBC,即AB3=1.71.5,所以AB=3.4 m.故答案为3.4 m.8.500解析 OAOA=2:5,可知OBOB=2:5.AOB=AOB,AOBAOB,ABAB=25,同理可得BCBC=2:5,矩形ABCD的面积:矩形ABCD的面积为425.又矩形ABCD的面积为80 cm2,则矩形ABCD的面积为500 cm2.9.6解析 实际动手折一个正方体,将数字标上

9、即可得解.10.(36-123)解析 将一张边长为6 cm的正方形纸片按虚线裁剪后,恰好围成一个底面是正六边形的棱柱,这个正六边形的底面边长为1 cm,该棱柱的侧面展开图是一个长为6 cm,宽为(6-23)cm的长方形,侧面积为6(6-23)=(36-123)cm2.11.1解析 主视图是第一层三个小正方形,第二层是左边一个小正方形,中间一个小正方形,第三层是左边一个小正方形;俯视图是第一行三个小正方形,第二行三个小正方形;左视图是第一层两个小正方形,第二层两个小正方形,第三层左边一个小正方形.不改变三视图,则中间第二层可以加一个.12.144解析 设余下扇形圆心角的度数为x,圆锥的底面周长为23=6,x5180=6,解得x=216,余下扇形的圆心角为216.n=360-216=144.13.解:(1)4(2)如图所示:14.解:(1)如图所示,线段AB即为所求.(2)如图,点O即为路灯灯泡的位置,线段CD为小周在灯光下的影子.15.解:(1)平行(2)如图,分别过点E,G作EMAB,GNCD,垂足分别是M,N,则有AEMCGN,MB=EF=2米,ME=BF=10米,ND=GH=3米,NG=DH=5米,AM=AB-MB=10-2=8(米),CN=CD-ND=(CD-3)米.CGNAEM,CNAM=NGME,即CD-38=510,CD=7米,即电线杆的高度是7米.